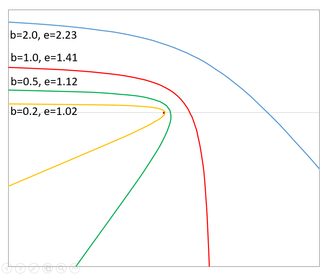
Trayectoria hiperbólica
En astrodinámica o mecánica celeste, una trayectoria hiperbólica es el recorrido descrito por un objeto con velocidad superior a la necesaria para escapar de la atracción gravitatoria de un cuerpo central.
Bajo suposiciones simplificadas, un cuerpo que viaje con esta trayectoria se dirigirá hacia el infinito, manteniendo una velocidad excedente final en relación con el cuerpo central.
Al igual que una órbita elíptica, se puede definir una trayectoria hiperbólica para un sistema dado (ignorando la orientación) por su semieje mayor y su excentricidad.
Sin embargo, con las órbita hiperbólica también se trabaja con otros parámetros que pueden ser más útiles para comprender el movimiento de un cuerpo.
La siguiente tabla enumera los parámetros principales que describen la ruta del cuerpo siguiendo una trayectoria hiperbólica alrededor de otro bajo supuestos estándar, y la fórmula que los relaciona.
Usualmente, por convención, es negativo, de forma consistente con varias ecuaciones relacionadas con órbitas elípticas.
El semieje mayor está directamente relacionado con la energía orbital específica (
es la energía característica, comúnmente utilizada en la planificación de misiones interplanetarias Téngase en cuenta que la energía total es positiva en el caso de una trayectoria hiperbólica (mientras que es negativa para una órbita elíptica).
, las asíntotas están a más de 120° de separación, y la distancia del periápside es mayor que el semieje mayor.
El ángulo entre la dirección de la periapsis y una asíntota del cuerpo central es la anomalía verdadera, ya que la distancia tiende al infinito (
Entonces El parámetro de impacto es la distancia por la cual un cuerpo, si continúa en un camino sin perturbaciones, pasará junto al cuerpo central en su punto más cercano.
Si se conocen las características del cuerpo central, es posible determinar la trayectoria, incluyendo la mínima distancia (es decir, la máxima aproximación) en el periápside.
Si esta distancia es menor que el radio del planeta, se debe esperar un impacto.
Si no se conoce la masa del cuerpo central, su parámetro gravitacional estándar, y por lo tanto su masa, puede determinarse por la deflexión del cuerpo más pequeño junto con el parámetro de impacto y la velocidad de aproximación.
) por la ecuación orbital: La relación entre la verdadera anomalía θ y la anomalía excéntrica E es: La anomalía excéntrica E está relacionada a su vez con la anomalía media M de la ecuación de Kepler: La anomalía media es proporcional al tiempo El ángulo de la trayectoria de vuelo (φ) es el ángulo formado entre la dirección de la velocidad y la dirección perpendicular a la radial, por lo que es cero en el periápside y tiende a 90 grados en el infinito.
Lo contrario también es cierto: un cuerpo no necesita reducir mucho su velocidad en relación con su exceso de velocidad hiperbólica (por ejemplo, mediante la resistencia atmosférica cerca del periápside) para que la velocidad caiga por debajo de la velocidad de escape y así pueda ser capturado por la gravedad del cuerpo principal.
Una trayectoria hiperbólica radial es un movimiento sobre una línea recta no periódico, en el que la velocidad relativa de los dos objetos siempre excede la velocidad de escape.
Esta situación se reduce a una órbita hiperbólica con un semieje menor = 0 y excentricidad = 1.
Aunque la excentricidad es 1, esta no se trata de una órbita parabólica.
No obstante, el término "trayectoria hiperbólica" se sigue utilizando para describir órbitas de este tipo.