Teorema de restricción cristalográfica
[1] Sin embargo, en los cuasicristales se pueden presentar otras simetrías, como la de orden 5, las cuales no fueron descubiertas hasta 1984 por el premio Nobel de Química 2011, Dan Shechtman.
La fuerza del teorema radica en que no todos los grupos finitos son compatibles con una red discreta.
Por ello, en cualquier dimensión, vamos a tener solamente un número finito de grupos compatibles.
Los casos especiales de los grupos planos 2D y los (grupos espaciales 3D son los más utilizados en las aplicaciones, y se pueden tratar juntos.
Ahora centraremos nuestra atención en el plano en que actúa la simetría.
Por tanto, se puede situar el origen de todos los vectores correspondientes a los lados del polígono en un mismo punto de la red.
La reducción del tamaño del polígono por aplicaciones sucesivas de este procedimiento es ilimitada: la misma estructura se puede repetir con el octágono nuevo y así sucesivamente hasta que la distancia entre dos puntos se convierte en infinitesimal.
Por lo tanto, no hay una red que pueda tener una simetría rotacional discreta de orden 8.
Si existe, entonces podemos tomar todos los desplazamientos entre puntos de la red y reunirlos (uniendo cabeza con cola) hasta formar una estrella de 5 puntas, con el extremo del último vector unido al punto de partida.
Los mosaicos de Penrose pueden tener simetría de rotación de orden 5 y una red discreta, y cualquier región local del embaldosado se repite infinitamente, pero no hay traslación lineal del embaldosado en su conjunto.
Y sin suponer que la red es discreta, no solo falla la construcción anterior hasta llegar a una contradicción, sino que produce un contraejemplo (red no discreta).
Del mismo modo, girando alrededor del punto A un ángulo θ, en la dirección opuesta, hace que B apunte a un nuevo punto B'.
Los cuatro vectores traslación (de los cuales tres están dadas por r, y uno que conecta A' y B' dado por r') forman un paralelogramo .
Se puede demostrar que los únicos valores de θ en el rango de 0° a 180° que satisfacen las tres ecuaciones anteriores son 0°, 60°, 90°, 120° y 180°.
Téngase en cuenta que las isometrías de orden n incluyen, pero no están solo restringidas, a las rotaciones de orden n. El teorema también excluye los grupos S8, S12, D4d, y D6d(véase grupos puntuales tridimensionales), aunque solamente haya simetría rotacional de orden 4 y 6.
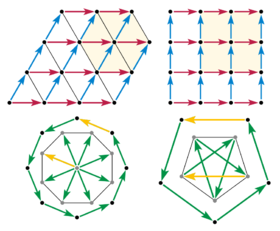
Compatible : orden 6 (orden 3), orden 4 (orden 2)
Incompatible : orden 8, orden 5