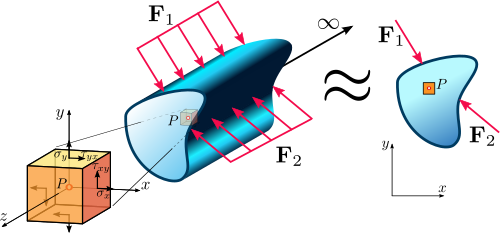
Teoría de la deformación infinitesimal
Con esta suposición, las ecuaciones de la mecánica del continuo se simplifican considerablemente.
Se adopta comúnmente en ingeniería civil y mecánica para el análisis de tensiones en estructuras construidas a partir de materiales elásticos relativamente rígidos, como el hormigón y el acero, ya que un objetivo común en el diseño de tales estructuras es minimizar su deformación bajo las cargas de diseño.
Sin embargo, esta aproximación exige precaución en el caso de cuerpos delgados y flexibles, como varillas, placas y carcasas, que son susceptibles de experimentar rotaciones importantes, lo que hace que los resultados no sean fiables.
y del tensor de deformación finita euleriano
En tal linealización, se desprecian los términos no lineales o de segundo orden del tensor de deformación finito.
Así, se obtiene o y o Esta linealización implica que la descripción lagrangiana y la descripción euleriana son aproximadamente iguales, ya que hay poca diferencia en las coordenadas materiales y espaciales de un punto material dado en el continuo.
son las componentes del tensor de deformación infinitesimal
o usando una notación diferente: Además, dado que el gradiente de deformación se puede expresar como
(Figura 1), que tras la deformación toma la forma de un rombo.
del elemento rectangular está definida por y sabiendo que
-direction, se vuelve El esfuerzo cortante, o el cambio de ángulo entre dos líneas de material originalmente ortogonales, en este caso las rectas
, se considera que y, nuevamente, para pequeños gradientes de desplazamiento, se tiene que y de este modo Al intercambiar
, como De la teoría de la deformación finita se tiene que Para deformaciones infinitesimales, entonces se sigue que Dividiendo por
, por lo que el segundo término del lado izquierdo se convierte en:
, y la expresión del lado izquierdo es la deformación normal
Por lo tanto, los elementos diagonales del tensor de deformaciones infinitesimales son las deformaciones normales en las direcciones de las coordenadas.
Si se elige un Sistema en coordenadas ortonormales (
) se denominan deformaciones principales y las direcciones
se denominan direcciones de deformación principales.
La deformación volumétrica, también llamada deformación del material, es la variación relativa del volumen que surge de la dilatación o de la compresión del sólido sometido a esfuerzos mecánicos; y es la primera invariante de deformación o la traza del tensor: En realidad, si se considera un cubo con una longitud de arista a, es un cuasi-cubo después de la deformación (las variaciones de los ángulos no cambian el volumen) con las dimensiones
Un plano octaédrico es aquel cuya normal forma ángulos iguales con las tres direcciones principales.
En la literatura se pueden encontrar varias definiciones de deformación equivalente.
Una definición que se usa comúnmente en la literatura sobre plasticidad es Esta cantidad es el trabajo conjugado con la tensión equivalente, definida como Para las componentes de deformación establecidas
Si el medio elástico se visualiza como un conjunto de cubos infinitesimales en estado no deformado, después de deformar el medio, un tensor de deformación arbitrario puede no producir una situación en la que los cubos distorsionados todavía encajen entre sí sin superponerse.
(si la longitud es la tercera dirección) están limitadas por el material cercano y son pequeñas en comparación con las deformaciones de la sección transversal.
sea distinto de cero para mantener la restricción
Este término de tensión se puede eliminar temporalmente del análisis para dejar solo los términos en el plano, reduciendo efectivamente el problema 3D a un problema 2D mucho más simple.
Un tensor de segundo orden simétrico oblicuo tiene tres componentes escalares independientes.
Estas tres componentes se utilizan para definir un vector axial,
y el tensor de deformación infinitesimal correspondiente