Sucesión (matemática)

En análisis matemático y en español una sucesión es una secuencia de números u otros objetos matemáticos relacionados entre sí, en la que se tiene en cuenta la posición relativa de cada letra respecto del anterior.A diferencia de un conjunto, el orden en que aparecen los términos sí es relevante y un mismo término puede aparecer en más de una posición.De manera formal, una sucesión puede definirse como una función sobre el conjunto de los números naturales (o un subconjunto del mismo) y es por tanto una función discreta.Existen diferentes notaciones y nociones de sucesión en matemática, dependiendo del área de estudio, algunas de las cuales (como por ejemplo sucesión exacta) no quedan comprendidas en la notación que se introduce a continuación.hace referencia al elemento de la sucesión en la posición n, llamado término general.Un ejemplo puede ser el de los números positivos pares, denotando dicha sucesión porEs frecuente encontrar sucesiones donde los subíndices que denoten posición inicien desde cero, en vez desde uno, particularmente en matemática discreta o en ciencias de la computación.También se puede usar una variable distinta a n para denotar el término general, cuando así convenga para evitar confusión con otras variables.En la literatura es posible encontrar una gran variedad de notaciones alternativas.En el primer caso la diferencia entre términos consecutivos es constante, mientras que en la segunda la razón o cociente entre términos consecutivos es constante: Progresión aritmética:fuesen los racionales, es decir fracciones enteras del tipo, se puede llamar sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos, trascendentes, … Una sucesión finita(de longitud r) con elementos pertenecientes a un conjunto S, se define como una funcióncon elementos pertenecientes a un conjunto S, se define como una función[1]​ En una sucesión monótona, la diferencia entre cada término y el siguiente es siempre del mismo signo.[2]​ Una sucesión creciente es aquella en la que se impone la desigualdad no estrictaDentro de estas se pueden incluir, entre otras, las sucesiones constantes.De la misma manera se puede definir la sucesión decreciente, según el término general, si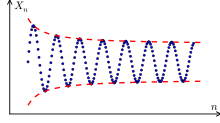Si una sucesión converge, esta tiende a un valor particular conocido como límite.(llamado límite de la sucesión), y se quedan «arbitrariamente» cercanos aSe puede comprobar fácilmente que si una sucesiónes único (se aplica reducción al absurdo y se llega a una contradicción) y la sucesión es acotada (consecuencia inmediata de la definición).Sus términos alternan indefinidamente de mayor a menor o viceversa, por lo que no tienen límite.Dada la sucesión {an} de números reales, se llama sucesión de Cauchy o sucesión fundamental, en el caso de que satisfaga el requisito siguiente: dado un número real r positivo se pueda conseguir dos enteros positivos p, q tal que de p > n0 y q > n0 se deduzca que |cp - cq| < r.[3]​ En los números reales toda sucesión de Cauchy converge a algún límite.Esta particularidad implica un resultado importante en el análisis real que es la caracterización de Cauchy para la convergencia de sucesiones: A los espacios métricos que verifiquen la implicación hacia la izquierda se les llama espacios completos.Es incorrecto representar a la extensión en los reales con el mismo nombre (), pues, se trata de una asociación totalmente arbitraria y no unívoca que trae confusión y no tiene sentido para algunas funciones definidas a trozos.La función f puede adquirir propiedades de la extendida P, si existe P con dichas propiedades, como límites al infinito, monotonía, acotaciones, entre otras., se define inductivamente por la sucesión de productos cartesianos siguiente:El complejo de cadenas simplicial del complejo simplicial K, no es más que una determinada sucesión de grupos abelianos y morfismos.