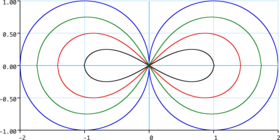
Lemniscata
[1][2] La palabra proviene del latín "lēmniscātus", que significa "decorado con cintas", a su vez procedente del griego "λημνίσκος" que significa "cintas",[2] que también puede referirse a la forma de la madeja de lana de la que se fabricaban las citadas cintas.
El estudio de las lemniscatas (y en particular de la hipopoda) se remonta a la matemática helénica, pero el término "lemniscata" para curvas de este tipo proviene del trabajo de Jakob Bernoulli a finales del siglo XVII.
La consideración de las curvas con una figura en forma de ocho se remonta a Proclo, un filósofo y matemático griego del neoplatonismo que vivió en el siglo V d. C. Proclo consideró las secciones de un toro por planos paralelos al eje del toro.
Como observó, para la mayoría de las secciones, la sección transversal consiste en uno o dos óvalos; sin embargo, cuando el plano es tangente a la superficie interna del toro, la sección transversal toma una figura con forma de ocho, a la que denominó con la palabra griega hipopoda (por su similitud con la atadura utilizada para inmovilizar dos de las patas de un caballo manteniéndolas juntas).
El nombre "lemniscata de Booth" para esta curva se remonta a su estudio por parte del matemático del siglo XIX James Booth.
[1] La lemniscata se puede definir como un curva algebraica, el conjunto de ceros del polinomio cuártico
Para valores positivos de d se obtiene una hipopoda.
En circunstancias muy particulares (cuando la mitad de la distancia entre los focos es igual a la raíz cuadrada de la constante), esto da lugar a una lemniscata de Bernouilli.
Al igual que la hipopoda, es una curva algebraica, el conjunto de ceros del polinomio
El hermano de Bernoulli, Jakob Bernoulli, también estudió la misma curva ese mismo año, y le dio su nombre.
, y puede formarse como una sección transversal de un toro tal que su orificio interno y sus secciones circulares tienen el mismo diámetro.
[1] Las funciones lemniscáticas elípticas son las análogas a las funciones trigonométricas para la lemniscata de Bernoulli, y las constantes de la lemniscata surgen al calcular la longitud de arco de este curva.
[8] Otras curvas algebraicas en forma de figura ocho incluyen: En geometría analítica, considérese n puntos del plano F1, F2, ...,Fn y k un número real estrictamente positivo.
El conjunto de los puntos del plano cuyo producto de las distancias a cada uno de los puntos F1, F2,...,Fn es constante e igual a k es una curva (lugar geométrico) llamada lemniscata de n focos.
La ecuación de la lemniscata en el plano complejo es Una secuencia arbitraria puede aproximarse a una curva arbitraria.
En particular, al tomar un número diferente de focos, organizarlos de manera diferente y asignar uno u otro valor para producir distancias, se pueden obtener los elementos más extraños, por ejemplo, el contorno de una cabeza humana o un ave.