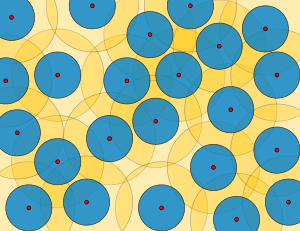
Conjunto de Delaunay
Un conjunto es uniformemente discreto si tiene un empaquetado de radio no nulo, y relativamente denso si tiene un radio de cobertura finito.
Un conjunto de Delaunay es a la vez uniformemente discreto y relativamente denso; así, toda ε-red es un conjunto de Delaunay, pero no al revés.
[3][4] Para espacios métricos finitos o compactos más generales, un algoritmo alternativo es el de Teo González, basado en el criterio del primer recorrido más lejano, que suele usarse para construir ε-redes finitas.
Como demuestran, este paradigma se suele poder utilizar para construir algoritmos de aproximación rápida para nubes de k-centros, encontrando un par de puntos con distancia media, y resolver muchos otros problemas relacionados.
Los conjuntos de Meyer deben su denominación a Yves Meyer, quien los introdujo (con una definición diferente pero equivalente basada en el análisis armónico) como modelo matemático para cuasicristales.