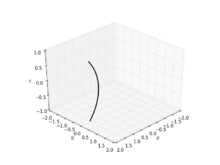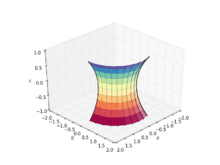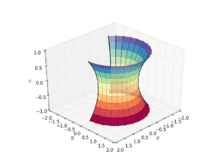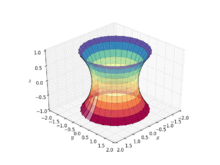
Catenoide

[1]​ Se trata de una superficie mínima o minimal, lo que significa que ocupa el área mínima cuando está delimitada por un espacio cerrado.[2]​ Fue descrita formalmente en 1744 por el matemático Leonhard Euler.La catenoide fue la primera superficie mínima no trivial en el espacio euclidiano tridimensional que se descubrió aparte del plano.La catenoide se obtiene al rotar una catenaria sobre su directriz.[3]​ Fue encontrada y probado que era un mínimo por Leonhard Euler en 1744.[4]​[5]​ El primer trabajo sobre el tema fue publicado también por Jean Baptiste Meusnier.[7]​ La catenoide se puede definir mediante las siguientes ecuaciones paramétricas:una constante real distinta de cero.Se puede formar un modelo físico de una catenoide sumergiendo dos anillos circulares en una solución jabonosa y separando lentamente los círculos.La catenoide también se puede definir aproximadamente mediante el método de cuadrícula estirada como un modelo 3D facetado.Una parametrización de tal deformación es dada por el sistema:y ( u , v ) = − cos ⁡ θ