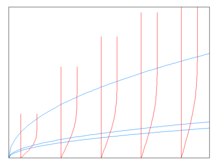
Capa límite de Blasius

En física y mecánica de fluidos, una capa límite de Blasius, llamada así por Paul Richard Heinrich Blasius, describe la capa límite laminar bidimensional constante que se forma en una placa semi-infinita que se mantiene paralela a un flujo unidireccional constante.Falkner y Skan generalizaron posteriormente la solución de Blasius al flujo en cuña (capa límite de Falkner-Skan), es decir, a los flujos en los que la placa no es paralela al flujo.Esto conduce a un conjunto reducido de ecuaciones conocidas como ecuaciones de la capa límite.Para un flujo incompresible constante con viscosidad y densidad constantes, dichas ecuaciones son: Continuidad de masas:Aquí el sistema de coordenadas se elige conapuntando paralelo a la placa en la dirección del flujo y la coordenadaSe han encontrado varias soluciones de similitud para este conjunto de ecuaciones para diversos tipos de flujo, incluido el flujo sobre una placa plana delgada.La solución autosimilar existe porque las ecuaciones y las condiciones de contorno son invariantes bajo la transformación dondey obtenidas sus derivadas, la ecuación de Prandtl-momentum puede ser adimensionalizada y reordenada para obtener el gradiente de presiónasciende a la velocidad de la corriente librepequeña es y la forma límite para grandesPara la solución de Blasius, vienen dadas por El factor[8]​ A esta solución puede añadirse cualquiera del conjunto discreto infinito de funciones propias, cada una de las cuales satisface la ecuación linealmente perturbada con condiciones homogéneas y decaimiento exponencial en el infinito.Esta aproximación de la capa límite predice una velocidad vertical distinta de cero lejos de la pared, que debe tenerse en cuenta en la capa externa no viscosa del siguiente orden y en la solución correspondiente de la capa límite interna, que a su vez predice una nueva velocidad vertical, y así sucesivamente.La solución para la capa límite externa no viscosa e interna son[7]​: 134 De nuevo como en el problema de frontera de primer orden, a esta solución se le puede añadir cualquiera del conjunto infinito de eigensoluciones.Dado que el problema interno de segundo orden es cero, las correcciones correspondientes al problema de tercer orden son nulas, es decir, el problema externo de tercer orden es el mismo que el problema externo de segundo orden.no es única y el problema queda con una constante indeterminada.[9]​ Considérese una velocidad de succión uniforme en la paredBryan Thwaites[10]​ demostró que la solución para este problema es la misma que la solución de Blasius sin succión para distancias muy próximas al borde de ataque.Introduciendo la transformación en las ecuaciones de la capa límite conduce a con las siguientes condiciones de contorno: Iglisch obtuvo la solución numérica completa en 1944.[11]​ Si además se introduce la transformación de von Mises[12]​ entonces las ecuaciones se convierten en: con las siguientes condiciones de contorno: Esta ecuación parabólica en derivadas parciales se puede plantear partiendo deDado que la convección debida a la succión y la difusión debida a la pared sólida actúan en sentido contrario, el perfil alcanzará solución estable a gran distancia, a diferencia del perfil de Blasius en el que la capa límite crece indefinidamente.La solución fue obtenida por primera vez por Griffith y F.W.[14]​ Aquí se estudia la capa límite de Blasius con una entalpía específica especificadaque representa propiedades evaluadas en el infinito.Las condiciones de contorno se convierten en A diferencia de la capa límite incompresible, la solución de similitud sólo existe si la transformación se cumple y esto sólo es posible siIntroduciendo las variables autosimilares mediante la transformación Howarth-Dorodnitsyn las ecuaciones se reducen a dondeLa temperatura dentro de la capa límite aumentará aunque la temperatura de la placa se mantenga a la misma temperatura que la ambiente, debido al calentamiento disipativo y, por supuesto, estos efectos de disipación sólo son pronunciados cuando el número de MachDado que las ecuaciones de la capa límite son ecuaciones parabólicas en derivadas parciales, las coordenadas naturales para el problema son coordenadas parabólicas.