Coordenadas parabólicas
constante forman parábolas confocales abiertas hacia arriba (en sentido
constante forman parábolas confocales abiertas hacia abajo (en sentido
Los focos de todas las parábolas se ubican en el origen.
equivalen a: Para un elemento infinitesimal de área es y su Laplaciano es: Otros operadores diferenciales tales como
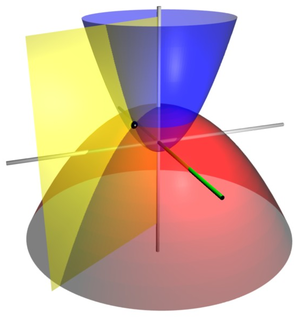
Las coordenadas cilíndricas parabólicas son producidas por proyección en la dirección
es constante forman paraboloides confocales con concavidades hacia arriba (o sea, en sentido
constante forman paraboloides confocales de concavidad hacia abajo (o sea, en sentido
Los focos de todos estos paraboloides están localizados en el origen.
El elemento infinitesimal de volumen es entonces Y el laplaciano es dado por Otros operadores diferenciales tales como
sustituyendo los factores de escala en las fórmulas generales encontradas en coordenadas ortogonales.
La conversión de coordenadas cartesianas a parabólicas se realiza a través de la siguiente transformación: El jacobiano de la transformación dada vincula términos infinitesimales como siendo Si φ = 0 se obtiene una sección transversal con las coordenadas limitadas al plano xz: Sea η=c (una constante), entonces Esta es una parábola con foco en el origen, para cualquier valor c. Su eje de simetría es vertical y su concavidad está orientada hacia arriba.
Se ξ=c entonces Esta es una parábola con foco en el origen, para cualquier valor de c. Su eje de simetría es vertical y su concavidad está orientada hacia abajo.
Si se desea encontrar su intersección: entonces y agrupando x² se cancelan los factores comunes de ambos lados tomando su raíz cuadrada, x es la media geométrica de b y c. Una vez hallada la abscisa de la intersección, se procede a obtener la ordenada.
Por lo tanto, el punto de intersección es Trácense ahora un par de tangentes a través del punto P, con una tangente en cada parábola.
Así mismo, un par de parábolas se cruzan en dos puntos, pero cuando φ es cero, en realidad limita las otras coordenadas ξ y η para moverse en el semiplano con x>0, ya que x<0 corresponde a φ = π.
Por lo tanto, un par de coordenadas ξ y η especifican un solo punto en el semiplano.
Al variar φ entre 0 y 2π, el semiplano vuelve al punto (alrededor del eje z, que es el eje de revolución): la fórmula de los paraboloides.