Bitangentes de una cuártica

Estas líneas existen en el plano proyectivo complejo, pero es posible definir curvas para las que todas estas 28 rectas bitangentes cuyas coordenadas son números reales, y por lo tanto pertenecen un espacio bidimensional.

Una cuártica explícita con veintiocho bitangentes reales fue hallada por primera vez por (txt,)[1]​ Como Plücker demostró, el número de bitangentes reales de cualquier cuártica debe ser 28, 16, o un número inferior a 9.

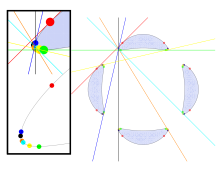
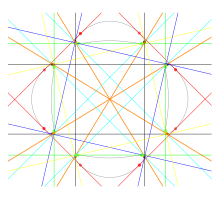
La curva de Trott, otra curva con 28 bitangentes reales, es el conjunto de puntos (x, y) que satisface la ecuación polinomial de cuarto grado: Estos puntos forman una curva cuártica no singular, que tiene genus tres y que posee veintiocho bitangentes reales.

Además, cada óvalo limita una región no convexa del plano y tiene una bitangente que abarca la porción no convexa de su límite.

Las 28 bitangentes de una cuártica también pueden colocarse en correspondencia con símbolos de la forma Donde a, b, c, d, e y f son todos cero o uno y donde Existen 64 opciones para a, b, c, d, e y f, pero solo 28 de estas opciones producen una suma impar.