Centro de masa

Punto único donde la posición relativa ponderada de la masa distribuida suma cero

Este juguete utiliza los principios del centro de masa para mantener el equilibrio cuando está sentado sobre un dedo.

En física , el centro de masa de una distribución de masa en el espacio (a veces denominado baricentro o punto de equilibrio ) es el único punto en un momento dado donde la posición relativa ponderada de la masa distribuida suma cero. Para un cuerpo rígido que contiene su centro de masa, este es el punto al que se puede aplicar una fuerza para provocar una aceleración lineal sin una aceleración angular . Los cálculos en mecánica suelen simplificarse cuando se formulan con respecto al centro de masa. Es un punto hipotético donde se puede suponer que está concentrada toda la masa de un objeto para visualizar su movimiento. En otras palabras, el centro de masa es el equivalente en partículas de un objeto dado para la aplicación de las leyes de movimiento de Newton . ^[1]

En el caso de un único cuerpo rígido , el centro de masas está fijo en relación con el cuerpo, y si el cuerpo tiene una densidad uniforme , se ubicará en el centroide . El centro de masas puede estar ubicado fuera del cuerpo físico , como sucede a veces con los objetos huecos o de forma abierta, como una herradura . En el caso de una distribución de cuerpos separados, como los planetas del Sistema Solar , el centro de masas puede no corresponder a la posición de ningún miembro individual del sistema.

El centro de masas es un punto de referencia útil para los cálculos en mecánica que involucran masas distribuidas en el espacio, como el momento lineal y angular de los cuerpos planetarios y la dinámica de cuerpos rígidos . En mecánica orbital , las ecuaciones de movimiento de los planetas se formulan como masas puntuales ubicadas en los centros de masas (ver Baricentro (astronomía) para más detalles). El marco del centro de masas es un marco inercial en el que el centro de masas de un sistema está en reposo con respecto al origen del sistema de coordenadas .

Historia

El concepto de centro de gravedad o peso fue estudiado extensamente por el matemático , físico e ingeniero griego Arquímedes de Siracusa . Trabajó con suposiciones simplificadas sobre la gravedad que equivalen a un campo uniforme, llegando así a las propiedades matemáticas de lo que ahora llamamos el centro de masa. Arquímedes demostró que el torque ejercido sobre una palanca por pesos que descansan en varios puntos a lo largo de la palanca es el mismo que el que sería si todos los pesos se movieran a un solo punto: su centro de masa. En su obra Sobre los cuerpos flotantes , Arquímedes demostró que la orientación de un objeto flotante es la que hace que su centro de masa sea lo más bajo posible. Desarrolló técnicas matemáticas para encontrar los centros de masa de objetos de densidad uniforme de varias formas bien definidas. ^[2]

Otros matemáticos antiguos que contribuyeron a la teoría del centro de masas incluyen a Herón de Alejandría y Pappus de Alejandría . En el Renacimiento y la Edad Moderna , el trabajo de Guido Ubaldi , Francesco Maurolico , ^[3] Federico Commandino , ^[4] Evangelista Torricelli , Simon Stevin , ^[5] Luca Valerio , ^[6] Jean-Charles de la Faille , Paul Guldin , ^[7] John Wallis , Christiaan Huygens , ^[8] Louis Carré , Pierre Varignon y Alexis Clairaut expandieron aún más el concepto. ^[9]

La segunda ley de Newton se reformula con respecto al centro de masa en la primera ley de Euler . ^[10]

Definición

El centro de masa es el único punto en el centro de una distribución de masa en el espacio que tiene la propiedad de que los vectores de posición ponderados relativos a este punto suman cero. En analogía con la estadística, el centro de masa es la ubicación media de una distribución de masa en el espacio.

Un sistema de partículas

En el caso de un sistema de partículas P _i , i = 1, ...,  n  , cada una con masa m _i que se encuentran en el espacio con coordenadas r _i , i = 1, ...,  n  , las coordenadas R del centro de masas satisfacen ∑ i = 1 n m i ( r i − R ) = 0 . {\displaystyle \sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )=\mathbf {0} .}

Resolviendo esta ecuación para R se obtiene la fórmula R = ∑ i = 1 n m i r i ∑ i = 1 n m i . {\displaystyle \mathbf {R} ={\sum _{i=1}^{n}m_{i}\mathbf {r} _{i} \over \sum _{i=1}^{n}m_{i}}.}

Un volumen continuo

Si la distribución de masa es continua con la densidad ρ( r ) dentro de un sólido Q , entonces la integral de las coordenadas de posición ponderadas de los puntos en este volumen en relación con el centro de masa R sobre el volumen V es cero, es decir $${\displaystyle \iiint _{Q}\rho (\mathbf {r} )\left(\mathbf {r} -\mathbf {R} \right)dV=\mathbf {0} .}$$

Resuelva esta ecuación para las coordenadas R para obtener Donde M es la masa total en el volumen. $${\displaystyle \mathbf {R} ={\frac {1}{M}}\iiint _{Q}\rho (\mathbf {r} )\mathbf {r} \,dV,}$$

Si una distribución de masa continua tiene una densidad uniforme , lo que significa que ρ es constante, entonces el centro de masa es el mismo que el centroide del volumen. ^[11]

Coordenadas baricéntricas

Las coordenadas R del centro de masa de un sistema de dos partículas, P ₁ y P ₂ , con masas m ₁ y m ₂ están dadas por $${\displaystyle \mathbf {R} ={{m_{1}\mathbf {r} _{1}+m_{2}\mathbf {r} _{2}} \over m_{1}+m_{2}}.}$$

Deje que el porcentaje de la masa total dividida entre estas dos partículas varíe de 100% P ₁ y 0% P ₂ a 50% P ₁ y 50% P ₂ a 0% P ₁ y 100% P ₂ , entonces el centro de masa R se mueve a lo largo de la línea de P ₁ a P ₂ . Los porcentajes de masa en cada punto pueden verse como coordenadas proyectivas del punto R en esta línea, y se denominan coordenadas baricéntricas . Otra forma de interpretar el proceso aquí es el equilibrio mecánico de momentos alrededor de un punto arbitrario. El numerador da el momento total que luego se equilibra con una fuerza total equivalente en el centro de masa. Esto se puede generalizar a tres puntos y cuatro puntos para definir coordenadas proyectivas en el plano y en el espacio, respectivamente.

Sistemas con condiciones de contorno periódicas

En el caso de partículas de un sistema con condiciones de contorno periódicas, dos partículas pueden ser vecinas aunque se encuentren en lados opuestos del sistema. Esto ocurre a menudo en simulaciones de dinámica molecular , por ejemplo, en las que se forman cúmulos en ubicaciones aleatorias y, a veces, los átomos vecinos cruzan el límite periódico. Cuando un cúmulo se extiende a ambos lados del límite periódico, un cálculo ingenuo del centro de masas será incorrecto. Un método generalizado para calcular el centro de masas de los sistemas periódicos consiste en tratar cada coordenada, x e y y /o z , como si estuviera en un círculo en lugar de una línea. ^{[12] El cálculo toma la coordenada} x de cada partícula y la asigna a un ángulo, donde x _max es el tamaño del sistema en la dirección x y . A partir de este ángulo, se pueden generar dos nuevos puntos , que se pueden ponderar por la masa de la partícula para el centro de masas o se les puede dar un valor de 1 para el centro geométrico: $${\displaystyle \theta _{i}={\frac {x_{i}}{x_{\max }}}2\pi }$$ ${\displaystyle x_{i}\in [0,x_{\max })}$ ${\displaystyle (\xi _{i},\zeta _{i})}$ ${\displaystyle x_{i}}$ $${\displaystyle {\begin{aligned}\xi _{i}&=\cos(\theta _{i})\\\zeta _{i}&=\sin(\theta _{i})\end{aligned}}}$$

En el plano, estas coordenadas se encuentran en un círculo de radio 1. A partir de la recopilación de valores y de todas las partículas, se calculan los promedios y . ${\displaystyle (\xi ,\zeta )}$ ${\displaystyle \xi _{i}}$ ${\displaystyle \zeta _{i}}$ ${\displaystyle {\overline {\xi }}}$ ${\displaystyle {\overline {\zeta }}}$

$${\displaystyle {\begin{aligned}{\overline {\xi }}&={\frac {1}{M}}\sum _{i=1}^{n}m_{i}\xi _{i},\\{\overline {\zeta }}&={\frac {1}{M}}\sum _{i=1}^{n}m_{i}\zeta _{i},\end{aligned}}}$$donde M es la suma de las masas de todas las partículas.

Estos valores se vuelven a asignar a un nuevo ángulo, , a partir del cual se puede obtener la coordenada x del centro de masa: ${\displaystyle {\overline {\theta }}}$

$${\displaystyle {\begin{aligned}{\overline {\theta }}&=\operatorname {atan2} \left(-{\overline {\zeta }},-{\overline {\xi }}\right)+\pi \\x_{\text{com}}&=x_{\max }{\frac {\overline {\theta }}{2\pi }}\end{aligned}}}$$

El proceso se puede repetir para todas las dimensiones del sistema para determinar el centro de masa completo. La utilidad del algoritmo es que permite a las matemáticas determinar dónde está el "mejor" centro de masa, en lugar de adivinar o usar el análisis de conglomerados para "desplegar" un conglomerado que se extiende a ambos lados de los límites periódicos. Si ambos valores promedio son cero, , entonces no está definido. Este es un resultado correcto, porque solo ocurre cuando todas las partículas están espaciadas de manera exactamente uniforme. En esa condición, sus coordenadas x son matemáticamente idénticas en un sistema periódico . ${\displaystyle \left({\overline {\xi }},{\overline {\zeta }}\right)=(0,0)}$ ${\displaystyle {\overline {\theta }}}$

Centro de gravedad

Diagrama de un juguete educativo que se equilibra sobre un punto: el centro de masa (C) se asienta debajo de su soporte (P)

El centro de gravedad de un cuerpo es el punto alrededor del cual desaparece el par resultante debido a las fuerzas de gravedad. ^[13] Cuando un campo de gravedad puede considerarse uniforme, el centro de masas y el centro de gravedad serán los mismos. Sin embargo, en el caso de los satélites en órbita alrededor de un planeta, en ausencia de otros pares aplicados a un satélite, la ligera variación (gradiente) en el campo gravitacional entre más cerca y más lejos del planeta (gravedad más fuerte y más débil respectivamente) puede generar un par que tenderá a alinear el satélite de manera que su eje largo sea vertical. En tal caso, es importante hacer la distinción entre el centro de gravedad y el centro de masas. ^[14] Cualquier desplazamiento horizontal entre los dos dará como resultado un par aplicado.

El centro de masa es una propiedad fija para un cuerpo rígido determinado (por ejemplo, sin movimiento ni articulación), mientras que el centro de gravedad puede, además, depender de su orientación en un campo gravitatorio no uniforme. En este último caso, el centro de gravedad siempre estará ubicado algo más cerca del cuerpo atractivo principal en comparación con el centro de masa y, por lo tanto, cambiará su posición en el cuerpo de interés a medida que se modifique su orientación.

En el estudio de la dinámica de aeronaves, vehículos y embarcaciones, las fuerzas y los momentos deben resolverse en relación con el centro de masas. Esto es así independientemente de si se tiene en cuenta la gravedad en sí. Referirse al centro de masas como centro de gravedad es algo coloquial, pero es de uso común y, cuando los efectos del gradiente de gravedad son insignificantes, centro de gravedad y centro de masas son lo mismo y se utilizan indistintamente.

En física, los beneficios de utilizar el centro de masas para modelar una distribución de masas se pueden ver al considerar la resultante de las fuerzas de gravedad sobre un cuerpo continuo. Considere un cuerpo Q de volumen V con densidad ρ ( r ) en cada punto r en el volumen. En un campo de gravedad paralelo, la fuerza f en cada punto r está dada por, donde dm es la masa en el punto r , g es la aceleración de la gravedad y es un vector unitario que define la dirección vertical. $${\displaystyle \mathbf {f} (\mathbf {r} )=-dm\,g\mathbf {\hat {k}} =-\rho (\mathbf {r} )\,dV\,g\mathbf {\hat {k}} ,}$$ ${\textstyle \mathbf {\hat {k}} }$

Elija un punto de referencia R en el volumen y calcule la fuerza y ​​el torque resultantes en este punto, F = ∭ Q f ( r ) d V = ∭ Q ρ ( r ) d V ( − g k ^ ) = − M g k ^ , {\displaystyle \mathbf {F} =\iiint _{Q}\mathbf {f} (\mathbf {r} )\,dV=\iiint _{Q}\rho (\mathbf {r} )\,dV\left(-g\mathbf {\hat {k}} \right)=-Mg\mathbf {\hat {k}} ,} y T = ∭ Q ( r − R ) × f ( r ) d V = ∭ Q ( r − R ) × ( − g ρ ( r ) d V k ^ ) = ( ∭ Q ρ ( r ) ( r − R ) d V ) × ( − g k ^ ) . {\displaystyle \mathbf {T} =\iiint _{Q}(\mathbf {r} -\mathbf {R} )\times \mathbf {f} (\mathbf {r} )\,dV=\iiint _{Q}(\mathbf {r} -\mathbf {R} )\times \left(-g\rho (\mathbf {r} )\,dV\, \mathbf {\hat {k}} \right)=\left(\iiint _ {Q}\rho (\mathbf {r} )\left(\mathbf {r} -\mathbf {R} \right)dV\right)\times \left(-g\mathbf {\hat {k}} \right).}

Si se elige el punto de referencia R de modo que sea el centro de masas, entonces el par resultante T = 0. Como el par resultante es cero, el cuerpo se moverá como si fuera una partícula con su masa concentrada en el centro de masas. $${\displaystyle \iiint _{Q}\rho (\mathbf {r} )\left(\mathbf {r} -\mathbf {R} \right)dV=0,}$$

Al seleccionar el centro de gravedad como punto de referencia para un cuerpo rígido, las fuerzas de gravedad no harán que el cuerpo gire, lo que significa que se puede considerar que el peso del cuerpo está concentrado en el centro de masa.

Momento lineal y angular

El momento lineal y angular de un conjunto de partículas se puede simplificar midiendo la posición y la velocidad de las partículas en relación con el centro de masas. Sea el sistema de partículas P _i , i = 1, ..., n de masas m _i ubicado en las coordenadas r _i con velocidades v _i . Seleccione un punto de referencia R y calcule los vectores de posición y velocidad relativos. $${\displaystyle \mathbf {r} _{i}=(\mathbf {r} _{i}-\mathbf {R} )+\mathbf {R} ,\quad \mathbf {v} _{i}={\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\mathbf {v} .}$$

El momento lineal total y el momento angular del sistema son p = d d t ( ∑ i = 1 n m i ( r i − R ) ) + ( ∑ i = 1 n m i ) v , {\displaystyle \mathbf {p} ={\frac {d}{dt}}\left(\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\right)+\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {v} ,} y L = ∑ i = 1 n m i ( r i − R ) × d d t ( r i − R ) + ( ∑ i = 1 n m i ) [ R × d d t ( r i − R ) + ( r i − R ) × v ] + ( ∑ i = 1 n m i ) R × v {\displaystyle \mathbf {L} =\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\left(\sum _{i=1}^{n}m_{i}\right)\left[\mathbf {R} \times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+(\mathbf {r} _{i}-\mathbf {R} )\times \mathbf {v} \right]+\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {R} \times \mathbf {v} }

Si se elige R como el centro de masa, estas ecuaciones se simplifican a donde m es la masa total de todas las partículas, p es el momento lineal y L es el momento angular. $${\displaystyle \mathbf {p} =m\mathbf {v} ,\quad \mathbf {L} =\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\sum _{i=1}^{n}m_{i}\mathbf {R} \times \mathbf {v} }$$

La ley de conservación del momento predice que, en cualquier sistema que no esté sujeto a fuerzas externas, el momento del sistema permanecerá constante, lo que significa que el centro de masas se moverá con velocidad constante. Esto se aplica a todos los sistemas con fuerzas internas clásicas, incluidos los campos magnéticos, los campos eléctricos, las reacciones químicas, etc. Más formalmente, esto es cierto para cualquier fuerza interna que se cancele de acuerdo con la Tercera Ley de Newton . ^[15]

Determinación

Método de la plomada

La determinación experimental del centro de masa de un cuerpo utiliza las fuerzas de gravedad sobre el cuerpo y se basa en el hecho de que el centro de masa es el mismo que el centro de gravedad en el campo de gravedad paralelo cerca de la superficie de la Tierra.

El centro de masas de un cuerpo con eje de simetría y densidad constante debe estar sobre este eje. Así, el centro de masas de un cilindro circular de densidad constante tiene su centro de masas sobre el eje del cilindro. De la misma manera, el centro de masas de un cuerpo esféricamente simétrico de densidad constante está en el centro de la esfera. En general, para cualquier simetría de un cuerpo, su centro de masas será un punto fijo de esa simetría. ^[16]

En dos dimensiones

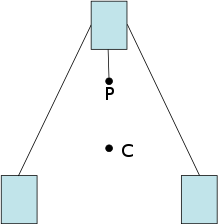
Un método experimental para localizar el centro de masas consiste en suspender el objeto de dos posiciones y dejar caer plomadas desde los puntos de suspensión. La intersección de las dos líneas es el centro de masas. ^[17]

La forma de un objeto puede estar ya determinada matemáticamente, pero puede ser demasiado compleja para utilizar una fórmula conocida. En este caso, se puede subdividir la forma compleja en formas más simples y elementales, cuyos centros de masa son fáciles de encontrar. Si se puede determinar la masa total y el centro de masa para cada área, entonces el centro de masa del conjunto es el promedio ponderado de los centros. ^[18] Este método puede funcionar incluso para objetos con agujeros, que pueden contabilizarse como masas negativas. ^[19]

Un desarrollo directo del planímetro, conocido como integráfono o enterometro, se puede utilizar para establecer la posición del centroide o centro de masa de una forma bidimensional irregular. Este método se puede aplicar a una forma con un límite irregular, liso o complejo donde otros métodos son demasiado difíciles. Los constructores de barcos lo utilizaban regularmente para comparar con el desplazamiento requerido y el centro de flotabilidad de un barco, y asegurarse de que no volcara. ^{[20] [21]}

En tres dimensiones

Un método experimental para localizar las coordenadas tridimensionales del centro de masas comienza sosteniendo el objeto en tres puntos y midiendo las fuerzas, F ₁ , F ₂ y F ₃ que resisten el peso del objeto, ( es el vector unitario en la dirección vertical). Sean r ₁ , r ₂ y r ₃ las coordenadas de posición de los puntos de apoyo, entonces las coordenadas R del centro de masas satisfacen la condición de que el torque resultante sea cero, o ${\displaystyle \mathbf {W} =-W\mathbf {\hat {k}} }$ ${\displaystyle \mathbf {\hat {k}} }$ $${\displaystyle \mathbf {T} =(\mathbf {r} _{1}-\mathbf {R} )\times \mathbf {F} _{1}+(\mathbf {r} _{2}-\mathbf {R} )\times \mathbf {F} _{2}+(\mathbf {r} _{3}-\mathbf {R} )\times \mathbf {F} _{3}=0,}$$ $${\displaystyle \mathbf {R} \times \left(-W\mathbf {\hat {k}} \right)=\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\mathbf {r} _{3}\times \mathbf {F} _{3}.}$$

Esta ecuación produce las coordenadas del centro de masa R * en el plano horizontal como, $${\displaystyle \mathbf {R} ^{*}=-{\frac {1}{W}}\mathbf {\hat {k}} \times (\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\mathbf {r} _{3}\times \mathbf {F} _{3}).}$$

El centro de masa se encuentra en la línea vertical L , dada por $${\displaystyle \mathbf {L} (t)=\mathbf {R} ^{*}+t\mathbf {\hat {k}} .}$$

Las coordenadas tridimensionales del centro de masas se determinan realizando este experimento dos veces con el objeto posicionado de manera que se midan estas fuerzas para dos planos horizontales diferentes que atraviesan el objeto. El centro de masas será la intersección de las dos líneas L ₁ y L ₂ obtenidas de los dos experimentos.

Aplicaciones

Diseños de ingeniería

Aplicaciones automotrices

Los ingenieros intentan diseñar un coche deportivo de forma que su centro de masas esté más bajo para que el coche se maneje mejor, es decir, mantenga la tracción al ejecutar curvas relativamente cerradas.

El perfil bajo característico del Humvee militar estadounidense fue diseñado en parte para permitirle inclinarse más que vehículos más altos sin volcarse , asegurando que su bajo centro de masas permanezca sobre el espacio delimitado por las cuatro ruedas incluso en ángulos alejados de la horizontal .

Aeronáutica

El centro de masa es un punto importante en una aeronave , que afecta significativamente la estabilidad de la aeronave. Para garantizar que la aeronave sea lo suficientemente estable como para volar de manera segura, el centro de masa debe estar dentro de límites específicos. Si el centro de masa está por delante del límite delantero , la aeronave será menos maniobrable, posiblemente hasta el punto de no poder girar para despegar o hacer un aterrizaje brusco. ^[22] Si el centro de masa está detrás del límite trasero, la aeronave será más maniobrable, pero también menos estable y posiblemente lo suficientemente inestable como para que sea imposible volar. El brazo de momento del elevador también se reducirá, lo que hace que sea más difícil recuperarse de una condición de pérdida . ^[23]

En el caso de los helicópteros en vuelo estacionario , el centro de masas siempre está directamente debajo del cabezal del rotor . En vuelo hacia adelante, el centro de masas se moverá hacia adelante para equilibrar el par de inclinación negativo producido al aplicar el control cíclico para impulsar el helicóptero hacia adelante; en consecuencia, un helicóptero en vuelo de crucero vuela "con el morro hacia abajo" en vuelo nivelado. ^[24]

Astronomía

Dos cuerpos orbitando alrededor de su baricentro (cruz roja)

El centro de masas juega un papel importante en astronomía y astrofísica, donde comúnmente se lo conoce como baricentro . El baricentro es el punto entre dos objetos donde se equilibran entre sí; es el centro de masas donde dos o más cuerpos celestes orbitan entre sí. Cuando una luna orbita un planeta , o un planeta orbita una estrella , ambos cuerpos en realidad orbitan un punto que se encuentra alejado del centro del cuerpo primario (más grande). ^[25] Por ejemplo, la Luna no orbita el centro exacto de la Tierra , sino un punto en una línea entre el centro de la Tierra y la Luna, aproximadamente a 1.710 km (1.062 millas) por debajo de la superficie de la Tierra, donde se equilibran sus respectivas masas. Este es el punto alrededor del cual orbitan la Tierra y la Luna mientras viajan alrededor del Sol . Si las masas son más similares, por ejemplo, Plutón y Caronte , el baricentro quedará fuera de ambos cuerpos.

Aparejo y seguridad

Conocer la ubicación del centro de gravedad durante el aparejo es crucial, ya que puede resultar en lesiones graves o la muerte si se asume incorrectamente. Un centro de gravedad que se encuentra en el punto de elevación o por encima de él probablemente resultará en un incidente de vuelco. En general, cuanto más abajo del punto de elevación se encuentre el centro de gravedad, más seguro será el izaje. Hay otras cosas que considerar, como el desplazamiento de las cargas, la resistencia de la carga y la masa, la distancia entre los puntos de elevación y el número de puntos de elevación. En concreto, al seleccionar los puntos de elevación, es muy importante colocar el centro de gravedad en el centro y muy por debajo de los puntos de elevación. ^[26]

Movimiento corporal

En kinesiología y biomecánica, el centro de masa es un parámetro importante que ayuda a las personas a comprender su locomoción humana. Por lo general, el centro de masa de un ser humano se detecta con uno de dos métodos: el método de la tabla de reacción es un análisis estático que implica que la persona se acueste sobre ese instrumento y se use su ecuación de equilibrio estático para encontrar su centro de masa; el método de segmentación se basa en una solución matemática basada en el principio físico de que la suma de los torques de las secciones individuales del cuerpo, en relación con un eje específico , debe ser igual al torque de todo el sistema que constituye el cuerpo, medido en relación con el mismo eje. ^[27]

Mejoramiento

El método del centro de gravedad es un método de optimización convexa, que utiliza el centro de gravedad de la región factible.

Véase también

• Portal de física

• Baricentro
• Flotabilidad
• Centro de percusión
• Centro de presión (mecánica de fluidos)
• Centro de presión (locomoción terrestre)
• Centroide
• Circuncentro de masa
• Valor esperado
• Geometría del punto de masa
• Altura metacéntrica
• Centro de balanceo
• Distribución del peso

Notas

1. "10.3: El centro de masas". Physics LibreTexts . 17 de septiembre de 2019 . Consultado el 15 de octubre de 2024 .
2. Shore 2008, págs. 9-11.
3. Barón 2004, págs. 91–94.
4. Barón 2004, págs. 94–96.
5. Barón 2004, págs. 96-101.
6. Barón 2004, págs. 101–106.
7. Mancosu 1999, págs. 56–61.
8. Erlichson, H. (1996). "El descubrimiento de la fórmula del centro de oscilación por parte de Christian Huygens". American Journal of Physics . 64 (5): 571–574. Bibcode :1996AmJPh..64..571E. doi :10.1119/1.18156. ISSN  0002-9505.
9. Walton 1855, pág. 2.
10. Beatty 2006, pág. 29.
11. Levi 2009, pág. 85.
12. Bai y Breen 2008.
13. Resnick, R. y Halliday, D. (1962) Física , 9-1 “Centro de masa”, Wiley
14. Resnick, R. y Halliday, D. (1962) Física , 14-3 “Centro de gravedad”, Wiley
15. Kleppner y Kolenkow 1973, pág. 117.
16. Las conferencias de Feynman sobre física, vol. I, cap. 19: Centro de masa; momento de inercia
17. Kleppner y Kolenkow 1973, págs. 119-120.
18. Feynman, Leighton y Sands 1963, págs. 19.1–19.2.
19. Hamill 2009, págs. 20-21.
20. "La teoría y el diseño de la construcción naval británica". Amos Lowrey Ayre . p. 3 . Consultado el 20 de agosto de 2012 .
21. Sangwin 2006, pág. 7.
22. Administración Federal de Aviación 2007, pág. 1.4.
23. Administración Federal de Aviación 2007, pág. 1.3.
24. "Aerodinámica de helicópteros" (PDF) . pág. 82. Archivado desde el original (PDF) el 24 de marzo de 2012. Consultado el 23 de noviembre de 2013 .
25. Murray y Dermott 1999, págs. 45–47.
26. "Técnico en derrumbes estructurales: Módulo 4: Elevación y aparejos" (PDF) . FEMA.gov . Consultado el 27 de noviembre de 2019 .
27. Vint 2003, págs. 1–11.

Referencias

• Asimov, Isaac (1988) [1966], Comprensión de la física , Barnes & Noble Books, ISBN 978-0-88029-251-1
• Bai, Linge; Breen, David (2008). "Cálculo del centro de masa en un entorno 2D sin límites". Revista de herramientas gráficas, GPU y de juegos . 13 (4): 53–60. doi :10.1080/2151237X.2008.10129266. S2CID  40807367.
• Baron, Margaret E. (2004) [1969], Los orígenes del cálculo infinitesimal , Courier Dover Publications, ISBN 978-0-486-49544-6
• Beatty, Millard F. (2006), Principios de mecánica de ingeniería, volumen 2: dinámica: el análisis del movimiento , Conceptos y métodos matemáticos en ciencia e ingeniería, vol. 33, Springer, ISBN 978-0-387-23704-6
• De Silva, Clarence W. (2002), Manual de vibraciones y choques , CRC Press, ISBN 978-0-8493-1580-0
• Administración Federal de Aviación (2007), Manual de peso y balance de aeronaves (PDF) , United States Government Printing Office , archivado desde el original (PDF) el 2011-10-19 , consultado el 2011-10-23
• Feynman, Richard ; Leighton, Robert B. ; Sands, Matthew (1963), The Feynman Lectures on Physics , vol. 1 (sexta edición, edición de febrero de 1977), Addison-Wesley, ISBN 978-0-201-02010-6
• Frautschi, Steven C. ; Olenick, Richard P. ; Apostol, Tom M. ; Goodstein, David L. (1986), El universo mecánico: mecánica y calor, edición avanzada , Cambridge University Press, ISBN 978-0-521-30432-0
• Giambattista, Alan; Richardson, Betty McCarthy; Richardson, Robert Coleman (2007), Física universitaria, vol. 1 (2.ª ed.), McGraw-Hill Higher Education, ISBN 978-0-07-110608-5
• Goldstein, Herbert ; Poole, Charles; Safko, John (2001), Mecánica clásica (3.ª ed.), Addison Wesley, ISBN 978-0-201-65702-9
• Goldstein, Herbert ; Poole, Charles; Safko, John (2002), Mecánica clásica (3.ª ed.), Addison-Wesley, ISBN 978-0-201-65702-9
• Goodman, Lawrence E.; Warner, William H. (2001) [1964], Estática , Dover, ISBN 978-0-486-42005-9
• Hamill, Patrick (2009), Dinámica intermedia , Jones & Bartlett Learning, ISBN 978-0-7637-5728-1
• Jong, IG; Rogers, BG (1995), Ingeniería mecánica: estática , Saunders College Publishing, ISBN 978-0-03-026309-5
• Kleppner, Daniel ; Kolenkow, Robert (1973), Introducción a la mecánica (2.ª ed.), McGraw-Hill, ISBN 978-0-07-035048-9
• Levi, Mark (2009), El mecánico matemático: uso del razonamiento físico para resolver problemas, Princeton University Press, ISBN 978-0-691-14020-9
• Mancosu, Paolo (1999), Filosofía de las matemáticas y práctica matemática en el siglo XVII , Oxford University Press, ISBN 978-0-19-513244-1
• Millikan, Robert Andrews (1902), Mecánica, física molecular y calor: un curso universitario de doce semanas, Chicago: Scott, Foresman and Company , consultado el 25 de mayo de 2011
• Murray, Carl; Dermott, Stanley (1999), Dinámica del sistema solar , Cambridge University Press, ISBN 978-0-521-57295-8
• O'Donnell, Peter J. (2015), Dinámica esencial y relatividad , CRC Press, ISBN 978-1-466-58839-4
• Pollard, David D.; Fletcher, Raymond C. (2005), Fundamentos de geología estructural , Cambridge University Press, ISBN 978-0-521-83927-3
• Pytel, Andrew; Kiusalaas, Jaan (2010), Ingeniería mecánica: estática , vol. 1 (3.ª ed.), Cengage Learning, ISBN 978-0-495-29559-4
• Rosen, Joe; Gothard, Lisa Quinn (2009), Enciclopedia de ciencias físicas , Infobase Publishing, ISBN 978-0-8160-7011-4
• Sangwin, Christopher J. (2006), "Localización del centro de masa por medios mecánicos" (PDF) , Journal of the Oughtred Society , 15 (2), archivado desde el original (PDF) el 2011-10-05 , consultado el 2011-10-23
• Serway, Raymond A.; Jewett, John W. (2006), Principios de física: un texto basado en cálculo , vol. 1 (4.ª ed.), Thomson Learning, Bibcode :2006ppcb.book.....J, ISBN 978-0-534-49143-7
• Shirley, James H.; Fairbridge, Rhodes Whitmore (1997), Enciclopedia de ciencias planetarias , Springer, ISBN 978-0-412-06951-2
• Shore, Steven N. (2008), Fuerzas en la física: una perspectiva histórica , Greenwood Press, ISBN 978-0-313-33303-3
• Symon, Keith R. (1971), Mecánica (3.ª ed.), Addison-Wesley, ISBN 978-0-201-07392-8
• Tipler, Paul A.; Mosca, Gene (2004), Física para científicos e ingenieros , vol. 1A (5.ª ed.), WH Freeman and Company, ISBN 978-0-7167-0900-8
• Van Pelt, Michael (2005), Turismo espacial: aventuras en la órbita terrestre y más allá , Springer, ISBN 978-0-387-40213-0
• Vint, Peter (2003), "LAB: Centro de masa (centro de gravedad) del cuerpo humano" (PDF) , KIN 335 - Biomecánica , consultado el 18 de octubre de 2013
• Walton, William (1855), Una colección de problemas para ilustrar los principios de la mecánica teórica (2.ª ed.), Deighton, Bell & Co.

Enlaces externos

• El movimiento del centro de masa muestra que el movimiento del centro de masa de un objeto en caída libre es el mismo que el movimiento de un objeto puntual.
• El baricentro del Sistema Solar, simulaciones que muestran el efecto que cada planeta aporta al baricentro del Sistema Solar.