


La dinámica de bicicletas y motocicletas es la ciencia que estudia el movimiento de las bicicletas y motocicletas y sus componentes, debido a las fuerzas que actúan sobre ellas. La dinámica se enmarca en una rama de la física conocida como mecánica clásica . Los movimientos de interés de las bicicletas incluyen el equilibrio , la dirección , el frenado , la aceleración , la activación de la suspensión y la vibración . El estudio de estos movimientos comenzó a fines del siglo XIX y continúa en la actualidad. [1] [2] [3]
Tanto las bicicletas como las motocicletas son vehículos de una sola vía , por lo que sus movimientos tienen muchos atributos fundamentales en común y son fundamentalmente diferentes y más difíciles de estudiar que otros vehículos con ruedas como los diciclos , triciclos y cuatriciclos . [4] Al igual que con los monociclos , las bicicletas carecen de estabilidad lateral cuando están estacionarias y, en la mayoría de las circunstancias, solo pueden permanecer en posición vertical cuando se mueven hacia adelante. La experimentación y el análisis matemático han demostrado que una bicicleta se mantiene en posición vertical cuando se dirige para mantener su centro de masa sobre sus ruedas. Esta dirección generalmente la proporciona un ciclista o, en ciertas circunstancias, la propia bicicleta. Varios factores, incluida la geometría, la distribución de la masa y el efecto giroscópico, contribuyen en diversos grados a esta autoestabilidad, pero las hipótesis y afirmaciones de larga data de que un solo efecto, como el giroscópico o el de la pista , es el único responsable de la fuerza estabilizadora han sido desacreditadas. [1] [5] [6] [7]
Aunque mantenerse erguido puede ser el objetivo principal de los ciclistas principiantes, una motocicleta debe inclinarse para mantener el equilibrio en una curva: cuanto mayor sea la velocidad o menor el radio de giro , más inclinación se requiere. Esto equilibra el par de giro sobre las zonas de contacto de la rueda generado por la fuerza centrífuga debido al giro con el de la fuerza gravitacional . Esta inclinación generalmente se produce por una dirección momentánea en la dirección opuesta, llamada contradirección . A diferencia de otros vehículos con ruedas, la entrada de control principal en las motocicletas es el par de dirección , no la posición. [8]
Aunque son longitudinalmente estables cuando están estacionarias, las bicicletas suelen tener un centro de masas lo suficientemente alto y una distancia entre ejes lo suficientemente corta como para levantar una rueda del suelo con una aceleración o desaceleración suficiente. Al frenar, dependiendo de la ubicación del centro de masas combinado de la bicicleta y el ciclista con respecto al punto donde la rueda delantera hace contacto con el suelo, y si el freno delantero se aplica con suficiente fuerza, las bicicletas pueden: hacer que la rueda delantera patine, lo que puede o no resultar en un choque; o volcar la bicicleta y el ciclista sobre la rueda delantera. Una situación similar es posible al acelerar, pero con respecto a la rueda trasera. [9]

La historia del estudio de la dinámica de la bicicleta es casi tan antigua como la propia bicicleta. Incluye contribuciones de científicos famosos como Rankine , Appell y Whipple . [2] A principios del siglo XIX, Karl von Drais , a quien se le atribuye la invención del vehículo de dos ruedas llamado laufmaschine , velocipede , draisine y dandy horse , demostró que un ciclista podía equilibrar su dispositivo dirigiendo la rueda delantera. [2] En 1869, Rankine publicó un artículo en The Engineer repitiendo la afirmación de von Drais de que el equilibrio se mantiene dirigiendo en la dirección de una inclinación. [10] En 1897, la Academia Francesa de Ciencias hizo de la comprensión de la dinámica de la bicicleta el objetivo de su competencia Prix Fourneyron. Así, a finales del siglo XIX, Carlo Bourlet, Emmanuel Carvallo y Francis Whipple habían demostrado con la dinámica de carrocería rígida que algunas bicicletas de seguridad podían realmente equilibrarse si se movían a la velocidad adecuada. [2] Bourlet ganó el Premio Fourneyron y Whipple ganó el Premio Smith de la Universidad de Cambridge . [7] No está claro a quién se le debe atribuir el mérito de inclinar el eje de dirección desde la vertical, lo que ayuda a que esto sea posible. [11]
En 1970, David EH Jones publicó un artículo en Physics Today que mostraba que los efectos giroscópicos no son necesarios para que una persona equilibre una bicicleta. [6] Desde 1971, cuando identificó y nombró los modos de tambaleo, oscilación y vuelco, [12] Robin Sharp ha escrito regularmente sobre el comportamiento de las motocicletas y las bicicletas. [13] Mientras estaba en el Imperial College de Londres, trabajó con David Limebeer y Simos Evangelou. [14] A principios de la década de 1970, el Laboratorio Aeronáutico de Cornell (CAL, más tarde Calspan Corporation en Buffalo, NY, EE. UU.) fue patrocinado por la Schwinn Bicycle Company y otros para estudiar y simular la dinámica de bicicletas y motocicletas. Partes de este trabajo ahora se han publicado al público y se han publicado escaneos de más de 30 informes detallados en este sitio de Dinámica de bicicletas de TU Delft. Desde la década de 1990, Cossalter, et al., han estado investigando la dinámica de las motocicletas en la Universidad de Padua. Su investigación, tanto experimental como numérica, ha abarcado el tejido, [15] el bamboleo, [16] el traqueteo, [17] los simuladores, [18] el modelado de vehículos, [19] el modelado de neumáticos, [ 20] [21] el manejo, [22] [23] y las maniobras de tiempo mínimo de vuelta. [24] [25]
En 2007, Meijaard, et al., publicaron las ecuaciones linealizadas canónicas de movimiento , en las Actas de la Royal Society A , junto con la verificación por dos métodos diferentes. [2] Estas ecuaciones asumieron que los neumáticos rodaban sin resbalar, es decir, que iban hacia donde apuntaban, y que el ciclista estaba rígidamente unido al cuadro trasero de la bicicleta. En 2011, Kooijman, et al., publicaron un artículo en Science que mostraba que ni los efectos giroscópicos ni los llamados efectos de avance debido al avance son necesarios para que una bicicleta se equilibre. [1] Diseñaron una bicicleta de dos masas que las ecuaciones de movimiento predicen que es autoestable incluso con un avance negativo, la rueda delantera contacta el suelo frente al eje de dirección y con ruedas contrarrotativas para cancelar cualquier efecto giroscópico. Luego construyeron un modelo físico para validar esa predicción. Esto puede requerir que se reevalúen algunos de los detalles proporcionados a continuación sobre la geometría o la estabilidad de la dirección. La dinámica de la bicicleta fue nombrada como 26 de las 100 historias más importantes de 2011 por Discover . [26] En 2013, Eddy Merckx Cycles recibió más de 150.000 € de la Universidad de Gante para examinar la estabilidad de la bicicleta. [27]


Si consideramos que la bicicleta y el ciclista forman un único sistema, las fuerzas que actúan sobre dicho sistema y sus componentes pueden dividirse, a grandes rasgos, en dos grupos: internas y externas. Las fuerzas externas se deben a la gravedad, la inercia, el contacto con el suelo y el contacto con la atmósfera. Las fuerzas internas son causadas por el ciclista y por la interacción entre los componentes.
Al igual que con todas las masas, la gravedad atrae al ciclista y todos los componentes de la bicicleta hacia la tierra. En cada parche de contacto de los neumáticos hay fuerzas de reacción del suelo con componentes horizontales y verticales. Los componentes verticales contrarrestan principalmente la fuerza de la gravedad, pero también varían con el frenado y la aceleración. Para obtener más detalles, consulte la sección sobre estabilidad longitudinal a continuación. Los componentes horizontales, debido a la fricción entre las ruedas y el suelo, incluida la resistencia a la rodadura , son en respuesta a las fuerzas de propulsión , las fuerzas de frenado y las fuerzas de giro. Las fuerzas aerodinámicas debidas a la atmósfera son principalmente en forma de resistencia , pero también pueden ser de vientos cruzados . A velocidades normales de bicicleta en terreno llano, la resistencia aerodinámica es la mayor fuerza que resiste el movimiento hacia adelante. [28] : 188 A mayor velocidad, la resistencia aerodinámica se convierte abrumadoramente en la mayor fuerza que resiste el movimiento hacia adelante.
Las fuerzas de giro se generan durante las maniobras para mantener el equilibrio, además de simplemente cambiar la dirección de desplazamiento. Estas pueden interpretarse como fuerzas centrífugas en el marco de referencia de aceleración de la bicicleta y el ciclista; o simplemente como inercia en un marco de referencia inercial estacionario y no como fuerzas en absoluto. Las fuerzas giroscópicas que actúan sobre piezas giratorias, como las ruedas, el motor, la transmisión, etc., también se deben a la inercia de esas piezas giratorias. Se analizan más detalladamente en la sección sobre efectos giroscópicos a continuación.
Las fuerzas internas, aquellas entre los componentes de la bicicleta y el sistema del ciclista, son causadas principalmente por el ciclista o por fricción. Además de pedalear, el ciclista puede aplicar pares entre el mecanismo de dirección (horquilla delantera, manillar, rueda delantera, etc.) y el cuadro trasero, y entre el ciclista y el cuadro trasero. Existe fricción entre todas las piezas que se mueven una contra la otra: en el tren de transmisión , entre el mecanismo de dirección y el cuadro trasero, etc. Además de los frenos , que crean fricción entre las ruedas giratorias y las piezas del cuadro que no giran, muchas bicicletas tienen suspensiones delantera y trasera . Algunas motocicletas y bicicletas tienen un amortiguador de dirección para disipar la energía cinética no deseada, [14] [29] y algunas bicicletas tienen un resorte que conecta la horquilla delantera al cuadro para proporcionar un par progresivo que tiende a dirigir la bicicleta hacia adelante. En las bicicletas con suspensiones traseras, la retroalimentación entre el tren de transmisión y la suspensión es un problema que los diseñadores intentan manejar con varias configuraciones de enlace y amortiguadores . [30]
Los movimientos de una bicicleta se pueden agrupar aproximadamente en aquellos fuera del plano central de simetría: lateral; y aquellos en el plano central de simetría: longitudinal o vertical. Los movimientos laterales incluyen el equilibrio, la inclinación, la dirección y los giros. Los movimientos en el plano central de simetría incluyen rodar hacia adelante, por supuesto, pero también los stoppies , los caballitos , el frenado y la mayoría de las activaciones de la suspensión. Los movimientos de estos dos grupos están linealmente desacoplados, es decir, no interactúan entre sí en el primer orden . [2] Una bicicleta no controlada es lateralmente inestable cuando está estacionaria y puede ser lateralmente autoestable cuando se mueve en las condiciones adecuadas o cuando está controlada por un ciclista. Por el contrario, una bicicleta es longitudinalmente estable cuando está estacionaria y puede ser longitudinalmente inestable cuando experimenta suficiente aceleración o desaceleración.
De las dos, la dinámica lateral ha demostrado ser la más complicada, requiriendo un análisis dinámico tridimensional de múltiples cuerpos con al menos dos coordenadas generalizadas para analizar. Como mínimo, se requieren dos ecuaciones diferenciales acopladas de segundo orden para capturar los movimientos principales. [2] No es posible encontrar soluciones exactas, y en su lugar se deben utilizar métodos numéricos . [2] Todavía se pueden encontrar teorías en competencia sobre cómo se equilibran las bicicletas en forma impresa y en línea. Por otro lado, como se muestra en secciones posteriores, gran parte del análisis dinámico longitudinal se puede lograr simplemente con cinética planar y solo una coordenada.

Al hablar del equilibrio de la bicicleta, es necesario distinguir cuidadosamente entre " estabilidad ", "autoestabilidad" y " controlabilidad ". Investigaciones recientes sugieren que "la estabilidad de las bicicletas controlada por el ciclista está relacionada con su autoestabilidad". [1]
Una motocicleta se mantiene en posición vertical cuando se la dirige de modo que las fuerzas de reacción del suelo equilibran exactamente todas las demás fuerzas internas y externas que experimenta, como la gravitacional si se inclina, la inercial o centrífuga si está en una curva, la giroscópica si se la dirige y la aerodinámica si hay viento cruzado. [28] La dirección puede ser proporcionada por un conductor o, en determinadas circunstancias, por la propia motocicleta. [31] Esta autoestabilidad se genera por una combinación de varios efectos que dependen de la geometría, la distribución de la masa y la velocidad de avance de la motocicleta. Los neumáticos, la suspensión, la amortiguación de la dirección y la flexión del cuadro también pueden influir en ella, especialmente en las motocicletas.
Incluso cuando se mantiene relativamente inmóvil, un ciclista puede mantener el equilibrio de una bicicleta mediante el mismo principio. Mientras realiza una parada en pista, el ciclista puede mantener la línea entre las dos zonas de contacto bajo el centro de masa combinado dirigiendo la rueda delantera hacia un lado o hacia el otro y luego moviéndose hacia adelante y hacia atrás ligeramente para mover la zona de contacto delantera de un lado a otro según sea necesario. El movimiento hacia adelante se puede generar simplemente pedaleando. El movimiento hacia atrás se puede generar de la misma manera en una bicicleta de piñón fijo . De lo contrario, el ciclista puede aprovechar una pendiente oportuna del pavimento o inclinar la parte superior del cuerpo hacia atrás mientras los frenos están momentáneamente activados. [32]
Si la dirección de una bicicleta está bloqueada, resulta prácticamente imposible mantener el equilibrio mientras se conduce. Por otro lado, si se anula el efecto giroscópico de las ruedas giratorias de la bicicleta añadiendo ruedas que giran en sentido contrario, sigue siendo fácil mantener el equilibrio mientras se conduce. [5] [6] Otra forma de equilibrar una bicicleta, con o sin dirección bloqueada, es aplicando pares de torsión adecuados entre la bicicleta y el ciclista, de forma similar a la forma en que un gimnasta puede balancearse desde que está colgado hacia abajo en barras paralelas asimétricas , una persona puede empezar a balancearse en un columpio desde el reposo bombeando sus piernas, o un péndulo doble invertido puede controlarse con un actuador solo en el codo. [33]
El ciclista aplica un par al manillar para girar la rueda delantera y así controlar la inclinación y mantener el equilibrio. A altas velocidades, los ángulos de dirección pequeños mueven rápidamente los puntos de contacto con el suelo lateralmente; a bajas velocidades, se requieren ángulos de dirección mayores para lograr los mismos resultados en la misma cantidad de tiempo. Debido a esto, generalmente es más fácil mantener el equilibrio a altas velocidades. [34] Como la autoestabilidad generalmente ocurre a velocidades superiores a un cierto umbral, ir más rápido aumenta las posibilidades de que una bicicleta contribuya a su propia estabilidad.
Cuanto más adelante (más cerca de la rueda delantera) esté el centro de masa de la bicicleta y el ciclista, menos tendrá que moverse lateralmente la rueda delantera para mantener el equilibrio. [35] Por el contrario, cuanto más atrás (más cerca de la rueda trasera) esté el centro de masa, más movimiento lateral de la rueda delantera o más movimiento hacia delante de la bicicleta se requiere para recuperar el equilibrio. Esto puede notarse en bicicletas reclinadas de distancia entre ejes larga , choppers y bicicletas con caballitos . [36] También puede ser un desafío para las bicicletas de turismo que llevan una carga pesada de equipo sobre o incluso detrás de la rueda trasera. [37] La masa sobre la rueda trasera se puede controlar más fácilmente si es menor que la masa sobre la rueda delantera. [11]
Una bicicleta también es un ejemplo de péndulo invertido . Así como una escoba se equilibra más fácilmente en la mano que un lápiz, una bicicleta alta (con un centro de masa alto) puede ser más fácil de equilibrar cuando se conduce que una baja porque la tasa de inclinación de la bicicleta alta (la tasa a la que su ángulo de inclinación aumenta a medida que comienza a caer) será más lenta. [38] Sin embargo, un ciclista puede tener la impresión opuesta de una bicicleta cuando está parada. Una bicicleta muy pesada en la parte superior puede requerir más esfuerzo para mantenerse en posición vertical, cuando está detenida en el tráfico, por ejemplo, que una bicicleta que es igual de alta pero con un centro de masa más bajo. Este es un ejemplo de una palanca vertical de segunda clase . Una pequeña fuerza en el extremo de la palanca, el asiento o el manillar en la parte superior de la bicicleta, mueve más fácilmente una masa grande si la masa está más cerca del fulcro, donde los neumáticos tocan el suelo. Por esta razón se aconseja a los ciclistas de turismo llevar la carga en una posición baja en la bicicleta y colocar alforjas colgando a ambos lados de los portaequipajes delantero y trasero . [39]

Un factor que influye en la facilidad o dificultad de manejo de una bicicleta es el recorrido , la distancia que el punto de contacto con el suelo de la rueda delantera se arrastra detrás del punto de contacto con el suelo del eje de dirección. El eje de dirección es el eje sobre el que pivota todo el mecanismo de dirección (horquilla, manillar, rueda delantera, etc.). En los diseños de bicicletas tradicionales, con un eje de dirección inclinado hacia atrás desde la vertical, el recorrido positivo tiende a dirigir la rueda delantera en la dirección de una inclinación, independientemente de la velocidad de avance. [28] Esto se puede simular empujando una bicicleta estacionaria hacia un lado. La rueda delantera normalmente también se dirigirá hacia ese lado. En una inclinación, la gravedad proporciona esta fuerza. Sin embargo, la dinámica de una bicicleta en movimiento es más complicada y otros factores pueden contribuir a este efecto o restarle valor. [1]
El avance es una función del ángulo de dirección, el avance o inclinación de la horquilla y el tamaño de la rueda. Su relación se puede describir mediante esta fórmula: [40]
donde es el radio de la rueda, es el ángulo del cabezal medido en el sentido de las agujas del reloj desde la horizontal y es el desplazamiento o inclinación de la horquilla. El avance se puede aumentar aumentando el tamaño de la rueda, disminuyendo el ángulo del cabezal o disminuyendo la inclinación de la horquilla.
Cuanto más recorrido tenga una bicicleta tradicional, más estable se sentirá, [41] aunque demasiado recorrido puede hacer que una bicicleta parezca difícil de dirigir. Las bicicletas con recorrido negativo (donde la superficie de contacto está delante de donde el eje de dirección se cruza con el suelo), aunque todavía se pueden conducir, se informa que se sienten muy inestables. Normalmente, las bicicletas de carreras de carretera tienen más recorrido que las bicicletas de turismo, pero menos que las bicicletas de montaña. Las bicicletas de montaña están diseñadas con ángulos de dirección menos verticales que las bicicletas de carretera para tener un mayor recorrido y, por lo tanto, una mejor estabilidad para los descensos. Las bicicletas de turismo se construyen con un recorrido pequeño para permitir que el ciclista controle una bicicleta cargada con equipaje. Como consecuencia, una bicicleta de turismo sin carga puede sentirse inestable. En las bicicletas, el rastrillo de la horquilla , a menudo una curva en las palas de la horquilla hacia delante del eje de dirección, se utiliza para disminuir el recorrido. [42] Existen bicicletas con recorrido negativo, como la Python Lowracer, y se pueden conducir, y se ha demostrado que una bicicleta experimental con recorrido negativo es autoestable. [1]
En las motocicletas, el ángulo de inclinación se refiere al ángulo de la dirección, y el desplazamiento creado por el árbol triple se utiliza para disminuir el avance. [43]
Una pequeña encuesta realizada por Whitt y Wilson [28] encontró:
Sin embargo, estos rangos no son estrictos. Por ejemplo, LeMond Racing Cycles ofrece [44] ambas con horquillas que tienen 45 mm de avance o inclinación y ruedas del mismo tamaño:
La cantidad de recorrido que tiene una bicicleta en particular puede variar con el tiempo por varias razones. En las bicicletas con suspensión delantera, especialmente las horquillas telescópicas, comprimir la suspensión delantera, debido a un frenado fuerte, por ejemplo, puede hacer más pronunciado el ángulo del eje de dirección y reducir el recorrido. El recorrido también varía con el ángulo de inclinación y el ángulo de dirección, y generalmente disminuye desde un máximo cuando la bicicleta está en posición vertical y se dirige hacia adelante. [45] El recorrido puede disminuir a cero con ángulos de inclinación y dirección suficientemente grandes, lo que puede alterar la sensación de estabilidad de una bicicleta. [11] Finalmente, incluso el perfil del neumático delantero puede influir en cómo varía el recorrido a medida que se inclina y se dirige la bicicleta.
Una medida similar al recorrido, llamada recorrido mecánico , recorrido normal o recorrido verdadero , [46] es la distancia perpendicular desde el eje de dirección hasta el centroide de la zona de contacto de la rueda delantera.
Un factor que influye en la estabilidad direccional de una bicicleta es la distancia entre ejes , la distancia horizontal entre los puntos de contacto con el suelo de las ruedas delanteras y traseras. Para un desplazamiento dado de la rueda delantera, debido a alguna perturbación, el ángulo de la trayectoria resultante a partir de la original es inversamente proporcional a la distancia entre ejes. [9] Además, el radio de curvatura para un ángulo de dirección y un ángulo de inclinación dados es proporcional a la distancia entre ejes. [9] Finalmente, la distancia entre ejes aumenta cuando la bicicleta se inclina y se gira. En casos extremos, cuando el ángulo de inclinación es de 90° y la bicicleta se gira en la dirección de esa inclinación, la distancia entre ejes aumenta en el radio de las ruedas delanteras y traseras. [11]
Otro factor que también puede contribuir a la autoestabilidad de los diseños tradicionales de bicicletas es la distribución de masa en el mecanismo de dirección, que incluye la rueda delantera, la horquilla y el manillar. Si el centro de masa del mecanismo de dirección está delante del eje de dirección, entonces la fuerza de gravedad también hará que la rueda delantera se desvíe en la dirección de una inclinación. Esto se puede ver inclinando una bicicleta estacionaria hacia un lado. La rueda delantera normalmente también se desviará hacia ese lado independientemente de cualquier interacción con el suelo. [47] Otros parámetros, como la posición de adelante hacia atrás del centro de masa y la elevación del centro de masa también contribuyen al comportamiento dinámico de una bicicleta. [28] [47]
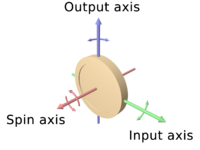
El papel del efecto giroscópico en la mayoría de los diseños de bicicletas es ayudar a dirigir la rueda delantera en la dirección de una inclinación. Este fenómeno se llama precesión , y la velocidad a la que un objeto precesa es inversamente proporcional a su velocidad de giro. Cuanto más lento gira una rueda delantera, más rápido precesará cuando la bicicleta se incline, y viceversa. [48] La fricción de los neumáticos contra el suelo impide que la rueda trasera precese, por lo que continúa inclinándose como si no estuviera girando en absoluto. Por lo tanto, las fuerzas giroscópicas no ofrecen ninguna resistencia al vuelco. [49]
A bajas velocidades de avance, la precesión de la rueda delantera es demasiado rápida, lo que contribuye a la tendencia de una bicicleta sin control a sobrevirar, comenzar a inclinarse hacia el otro lado y, finalmente, oscilar y caer. A altas velocidades de avance, la precesión suele ser demasiado lenta, lo que contribuye a la tendencia de una bicicleta sin control a subvirar y, finalmente, caer sin haber alcanzado nunca la posición vertical. [11] Esta inestabilidad es muy lenta, del orden de segundos, y es fácil de contrarrestar para la mayoría de los ciclistas. Por lo tanto, una bicicleta rápida puede parecer estable aunque en realidad no sea autoestable y se caería si no estuviera controlada.
Otra contribución de los efectos giroscópicos es el momento de balanceo generado por la rueda delantera durante el contra-mando. Por ejemplo, girar a la izquierda provoca un momento hacia la derecha. El momento es pequeño en comparación con el momento generado por la rueda delantera que se desplaza hacia afuera, pero comienza tan pronto como el conductor aplica par al manillar, por lo que puede ser útil en las carreras de motos . [9] Para obtener más detalles, consulte la sección sobre contra-mando, a continuación, y el artículo sobre contra-mando .
Entre los dos regímenes inestables mencionados en la sección anterior, e influenciados por todos los factores descritos anteriormente que contribuyen al equilibrio (arrastre, distribución de masa, efectos giroscópicos, etc.), puede haber un rango de velocidades de avance para un diseño de bicicleta determinado en el que estos efectos dirigen una bicicleta no controlada hacia arriba. [2] Se ha demostrado que ni los efectos giroscópicos ni el avance positivo son suficientes por sí mismos ni necesarios para la autoestabilidad, aunque ciertamente pueden mejorar el control de manos libres. [1]
Sin embargo, incluso sin autoestabilidad, se puede andar en bicicleta dirigiéndola para mantenerla sobre sus ruedas. [6] Tenga en cuenta que los efectos mencionados anteriormente que se combinarían para producir autoestabilidad pueden verse superados por factores adicionales como la fricción del juego de dirección y los cables de control rígidos . [28] Este video muestra una bicicleta sin ciclista que exhibe autoestabilidad.
Se ha demostrado que la aceleración longitudinal tiene un efecto amplio y complejo en la dinámica lateral. En un estudio, la aceleración positiva elimina la autoestabilidad, y la aceleración negativa (desaceleración) cambia las velocidades de la autoestabilidad. [7]


Para que una bicicleta gire, es decir, cambie su dirección de avance, la rueda delantera debe apuntar aproximadamente en la dirección deseada, como en cualquier vehículo con dirección delantera. La fricción entre las ruedas y el suelo genera entonces la aceleración centrípeta necesaria para alterar el rumbo desde el principio como una combinación de fuerza de viraje y empuje de inclinación . El radio de giro de una bicicleta en posición vertical (no inclinada) se puede aproximar aproximadamente, para ángulos de dirección pequeños , mediante:
donde es el radio aproximado, es la distancia entre ejes , es el ángulo de dirección y es el ángulo de avance del eje de dirección. [9]
Sin embargo, a diferencia de otros vehículos con ruedas, las bicicletas también deben inclinarse durante un giro para equilibrar las fuerzas relevantes: gravitacional, inercial, de fricción y de apoyo al suelo. El ángulo de inclinación, θ , se puede calcular fácilmente utilizando las leyes del movimiento circular :
donde v es la velocidad de avance, r es el radio de giro y g es la aceleración de la gravedad . [48] Esto es en el caso idealizado. Es posible que se requiera un ligero aumento en el ángulo de inclinación en las motocicletas para compensar el ancho de los neumáticos modernos a la misma velocidad de avance y radio de giro. [45]
Sin embargo, también se puede observar que este modelo bidimensional simple, que es esencialmente un péndulo invertido sobre una plataforma giratoria , predice que el giro en estado estable es inestable. Si la bicicleta se desplaza ligeramente hacia abajo desde su ángulo de inclinación de equilibrio, el par de gravedad aumenta, el de la fuerza centrífuga disminuye y el desplazamiento se amplifica. Es necesario un modelo más sofisticado que permita que una rueda gire, ajuste la trayectoria y contrarreste el par de gravedad para capturar la autoestabilidad observada en las bicicletas reales.
Por ejemplo, una bicicleta en un giro en estado estable de 10 m (33 pies) de radio a 10 m/s (36 km/h, 22 mph) debe estar en un ángulo de 45,6°. Un ciclista puede inclinarse con respecto a la bicicleta para mantener el torso o la bicicleta más o menos erguida si así lo desea. El ángulo que importa es el que se forma entre el plano horizontal y el plano definido por los contactos de los neumáticos y la ubicación del centro de masas de la bicicleta y el ciclista.
Esta inclinación de la motocicleta disminuye el radio real del giro proporcionalmente al coseno del ángulo de inclinación. El radio resultante se puede calcular aproximadamente (con un margen de error del 2 % del valor exacto) de la siguiente manera:
donde es el radio aproximado, es la distancia entre ejes, es el ángulo de inclinación, es el ángulo de dirección y es el ángulo de avance del eje de dirección. [9] A medida que una motocicleta se inclina, las zonas de contacto de los neumáticos se mueven más hacia los lados, lo que provoca desgaste. Las partes en cada borde de un neumático de motocicleta que permanecen sin desgastarse al inclinarse en las curvas a veces se denominan tiras de pollo.
El ancho finito de los neumáticos altera el ángulo de inclinación real del cuadro trasero con respecto al ángulo de inclinación ideal descrito anteriormente. El ángulo de inclinación real entre el cuadro y la vertical debe aumentar con el ancho de los neumáticos y disminuir con la altura del centro de masas. Las bicicletas con neumáticos anchos y un centro de masas bajo deben inclinarse más que las bicicletas con neumáticos más delgados o centros de masas más altos para sortear la misma curva a la misma velocidad. [9]
El aumento del ángulo de inclinación debido a un espesor de neumático de 2 t se puede calcular como
donde φ es el ángulo de inclinación ideal y h es la altura del centro de masas. [9] Por ejemplo, una motocicleta con un neumático trasero de 12 pulgadas de ancho tendrá t = 6 pulgadas. Si el centro de masas combinado de la motocicleta y el conductor está a una altura de 26 pulgadas, entonces una inclinación de 25° debe aumentarse en 7,28°: un aumento de casi el 30%. Si los neumáticos tienen solo 6 pulgadas de ancho, entonces el aumento del ángulo de inclinación es solo 3,16°, poco menos de la mitad.
La pareja creada por la gravedad y las fuerzas de reacción del suelo es necesaria para que una bicicleta pueda girar. En una bicicleta hecha a medida con estabilizadores accionados por resorte que cancelan exactamente esta pareja, de modo que la bicicleta y el ciclista pueden asumir cualquier ángulo de inclinación cuando viajan en línea recta, a los ciclistas les resulta imposible hacer un giro. Tan pronto como las ruedas se desvían de una trayectoria recta, la bicicleta y el ciclista comienzan a inclinarse en la dirección opuesta, y la única forma de enderezarlos es volver a la trayectoria recta. [50] [51]
Para iniciar un giro y la inclinación necesaria en la dirección de ese giro, una bicicleta debe virar momentáneamente en la dirección opuesta. Esto se conoce a menudo como contraviraje. Con la rueda delantera ahora en un ángulo finito con respecto a la dirección del movimiento, se desarrolla una fuerza lateral en la zona de contacto del neumático. Esta fuerza crea un par alrededor del eje longitudinal (de balanceo) de la bicicleta, y este par hace que la bicicleta se incline en dirección opuesta a la dirección inicial y hacia la dirección del giro deseado. Cuando no hay influencia externa, como un viento lateral oportuno para crear la fuerza necesaria para inclinar la bicicleta, es necesario contraviraje para iniciar un giro rápido. [48]
Si bien el par de dirección inicial y el ángulo de dirección son opuestos a la dirección de giro deseada, este puede no ser el caso para mantener un giro en estado estable. El ángulo de dirección sostenido generalmente está en la misma dirección que el giro, pero puede permanecer opuesto a la dirección del giro, especialmente a altas velocidades. [52] El par de dirección sostenido necesario para mantener ese ángulo de dirección generalmente es opuesto a la dirección de giro. [53] La magnitud y orientación reales tanto del ángulo de dirección sostenido como del par de dirección sostenido de una bicicleta en particular en un giro particular dependen de la velocidad de avance, la geometría de la bicicleta, las propiedades de los neumáticos y la distribución combinada de la masa de la bicicleta y el ciclista. [23] Una vez en un giro, el radio solo se puede cambiar con un cambio apropiado en el ángulo de inclinación, y esto se puede lograr con un contraviraje adicional fuera del giro para aumentar la inclinación y disminuir el radio, luego dentro del giro para disminuir la inclinación y aumentar el radio. Para salir del giro, la bicicleta debe contravirar nuevamente, girando momentáneamente más hacia el giro para disminuir el radio, aumentando así las fuerzas de inercia y, por lo tanto, disminuyendo el ángulo de inclinación. [54]
Una vez que se establece un giro, el par que se debe aplicar al mecanismo de dirección para mantener un radio constante a una velocidad de avance constante depende de la velocidad de avance y de la geometría y distribución de masa de la motocicleta. [11] [23] A velocidades inferiores a la velocidad de vuelco, descrita a continuación en la sección sobre valores propios y también llamada velocidad de inversión , la autoestabilidad de la motocicleta hará que tienda a virar hacia la curva, enderezándose y saliendo de la curva, a menos que se aplique un par en la dirección opuesta a la curva. A velocidades superiores a la velocidad de vuelco, la inestabilidad de vuelco hará que tienda a virar hacia afuera de la curva, aumentando la inclinación, a menos que se aplique un par en la dirección de la curva. A la velocidad de vuelco, no es necesario ningún par de dirección de entrada para mantener el giro en estado estable.
Varios efectos influyen en el ángulo de dirección, el ángulo en el que gira el conjunto delantero sobre el eje de dirección, necesario para mantener un giro estable. Algunos de ellos son exclusivos de los vehículos de una sola vía, mientras que otros también se dan en los automóviles. Algunos de ellos pueden mencionarse en otras partes de este artículo y se repiten aquí, aunque no necesariamente en orden de importancia, para que se puedan encontrar en un solo lugar.
En primer lugar, el ángulo de dirección cinemático real, el ángulo proyectado sobre el plano de la carretera hacia el que gira el conjunto delantero, es una función del ángulo de dirección y del ángulo del eje de dirección:
donde es el ángulo de dirección cinemático, es el ángulo de dirección y es el ángulo de avance del eje de dirección. [9]
En segundo lugar, la inclinación de la motocicleta disminuye el radio real del giro proporcionalmente al coseno del ángulo de inclinación. El radio resultante se puede calcular aproximadamente (con un margen de error del 2 % del valor exacto) de la siguiente manera:
donde es el radio aproximado, es la distancia entre ejes, es el ángulo de inclinación, es el ángulo de dirección y es el ángulo de avance del eje de dirección. [9]
En tercer lugar, debido a que los neumáticos delanteros y traseros pueden tener diferentes ángulos de deslizamiento debido a la distribución del peso, las propiedades de los neumáticos, etc., las motos pueden experimentar subviraje o sobreviraje . Cuando se subvira, el ángulo de dirección debe ser mayor, y cuando se sobrevira, el ángulo de dirección debe ser menor de lo que sería si los ángulos de deslizamiento fueran iguales para mantener un radio de giro determinado. [9] Algunos autores incluso utilizan el término contraviraje para referirse a la necesidad en algunas motos bajo ciertas condiciones de girar en la dirección opuesta del giro (ángulo de dirección negativo) para mantener el control en respuesta a un deslizamiento significativo de la rueda trasera. [9]
En cuarto lugar, el empuje de inclinación contribuye a la fuerza centrípeta necesaria para hacer que la motocicleta se desvíe de una trayectoria recta, junto con la fuerza de giro debido al ángulo de deslizamiento , y puede ser el mayor contribuyente. [45] El empuje de inclinación contribuye a la capacidad de las motocicletas para negociar una curva con el mismo radio que los automóviles pero con un ángulo de dirección más pequeño. [45] Cuando una motocicleta se dirige e inclina en la misma dirección, el ángulo de inclinación del neumático delantero es mayor que el del trasero y, por lo tanto, puede generar más empuje de inclinación, en igualdad de condiciones. [9]
Aunque el contraviraje suele iniciarse aplicando un par directamente al manillar, en vehículos más ligeros, como las bicicletas, se puede lograr desplazando el peso del ciclista. Si el ciclista se inclina hacia la derecha en relación con la bicicleta, la bicicleta se inclina hacia la izquierda para conservar el momento angular y el centro de masas combinado permanece casi en el mismo plano vertical. Esta inclinación hacia la izquierda de la bicicleta, llamada contrainclinación por algunos autores, [45] hará que se desvíe hacia la izquierda e inicie un giro hacia la derecha como si el ciclista hubiera contravirado hacia la izquierda aplicando un par directamente al manillar. [48] Esta técnica puede complicarse por factores adicionales, como la fricción del juego de dirección y los cables de control rígidos.
El centro de masas combinado se mueve ligeramente hacia la izquierda cuando el ciclista se inclina hacia la derecha en relación con la bicicleta, y la bicicleta se inclina hacia la izquierda en respuesta. La acción, en el espacio, haría que los neumáticos se movieran hacia la derecha, pero esto se evita por la fricción entre los neumáticos y el suelo, y por lo tanto empuja el centro de masas combinado hacia la izquierda. Sin embargo, este es un efecto pequeño, como lo demuestra la dificultad que la mayoría de las personas tienen para equilibrar una bicicleta solo con este método.
Como se mencionó anteriormente en la sección sobre el equilibrio, un efecto del giro de la rueda delantera es un momento de balanceo causado por la precesión giroscópica . La magnitud de este momento es proporcional al momento de inercia de la rueda delantera, su velocidad de giro (movimiento hacia adelante), la velocidad a la que el ciclista gira la rueda delantera al aplicar un par al manillar y el coseno [ ancla rota ] del ángulo entre el eje de dirección y la vertical. [9]
En el caso de una motocicleta de muestra que se mueve a 22 m/s (50 mph) y que tiene una rueda delantera con un momento de inercia de 0,6 kg·m 2 , girar la rueda delantera un grado en medio segundo genera un momento de balanceo de 3,5 N·m. En comparación, la fuerza lateral sobre el neumático delantero cuando sale de debajo de la motocicleta alcanza un máximo de 50 N. Esto, actuando sobre la altura de 0,6 m (2 ft) del centro de masa, genera un momento de balanceo de 30 N·m.
Si bien el momento de las fuerzas giroscópicas representa solo el 12 % de esto, puede desempeñar un papel importante porque comienza a actuar tan pronto como el conductor aplica el par, en lugar de aumentar más lentamente a medida que la rueda se desvía de su trayectoria. Esto puede ser especialmente útil en las carreras de motos .
Debido a los beneficios teóricos, como un radio de giro más estrecho a baja velocidad, se han hecho intentos de construir motocicletas con dirección en dos ruedas. Se informa que un prototipo funcional de Ian Drysdale en Australia "funciona muy bien". [55] [56] Los problemas en el diseño incluyen si proporcionar un control activo de la rueda trasera o dejar que se balancee libremente. En el caso del control activo, el algoritmo de control debe decidir entre girar con o en la dirección opuesta de la rueda delantera, cuándo y cuánto. Una implementación de dirección en dos ruedas, la bicicleta Sideways , permite al conductor controlar la dirección de ambas ruedas directamente. Otra, la Swing Bike , tenía el segundo eje de dirección delante del asiento para que también pudiera controlarse con el manillar.
Milton W. Raymond construyó una bicicleta de dirección de dos ruedas baja y larga, llamada "X-2", con varios mecanismos de dirección para controlar las dos ruedas de forma independiente. Los movimientos de dirección incluían "equilibrio", en el que ambas ruedas se mueven juntas para dirigir los contactos de los neumáticos debajo del centro de masa; y "círculo verdadero", en el que las ruedas giran por igual en direcciones opuestas y, por lo tanto, dirigen la bicicleta sin cambiar sustancialmente la posición lateral de los contactos de los neumáticos en relación con el centro de masa. X-2 también podía ir "en sentido cangrejo" con las ruedas paralelas pero desalineadas con el cuadro, por ejemplo, con la rueda delantera cerca de la línea central de la carretera y la rueda trasera cerca del bordillo . La dirección de "equilibrio" permitió un equilibrio fácil a pesar de la larga distancia entre ejes y el bajo centro de masa, pero no se descubrió ninguna configuración de autoequilibrio ("sin manos"). El círculo verdadero, como se esperaba, fue esencialmente imposible de equilibrar, ya que la dirección no corrige la desalineación del parche del neumático y el centro de masa. El ciclismo en sentido cangrejo en ángulos probados de hasta aproximadamente 45° no mostró una tendencia a caerse, incluso al frenar. [ cita requerida ] X-2 se menciona de pasada en Bicycling Science, segunda edición, de Whitt y Wilson. [28]
Debido a los beneficios teóricos, especialmente un mecanismo simplificado de tracción delantera , se han hecho intentos de construir una bicicleta con dirección en las ruedas traseras que se pueda conducir. La empresa Bendix construyó una bicicleta con dirección en las ruedas traseras y el Departamento de Transporte de los Estados Unidos encargó la construcción de una motocicleta con dirección en las ruedas traseras: ambas resultaron ser imposibles de conducir. Rainbow Trainers, Inc. en Alton, Illinois, ofreció 5.000 dólares estadounidenses a la primera persona "que pueda conducir con éxito la bicicleta con dirección trasera, Rear Steered Bicycle I". [57] Un ejemplo documentado de alguien que logró conducir con éxito una bicicleta con dirección en las ruedas traseras es el de LH Laiterman en el Instituto Tecnológico de Massachusetts, en una bicicleta reclinada especialmente diseñada. [28] La dificultad es que girar a la izquierda, lo que se logra girando la rueda trasera hacia la derecha, inicialmente mueve el centro de masas hacia la derecha, y viceversa. Esto complica la tarea de compensar las inclinaciones inducidas por el entorno. [58] El análisis de los valores propios de bicicletas con geometrías y distribuciones de masas comunes muestra que, cuando se desplazan en reversa, de modo que tengan dirección en las ruedas traseras, son inherentemente inestables. Esto no significa que no se puedan conducir, sino que el esfuerzo para controlarlas es mayor. [59] Sin embargo, se han publicado otros diseños diseñados específicamente para este fin que no sufren este problema. [1] [60]

Entre los extremos de las bicicletas con dirección clásica en las ruedas delanteras y aquellas con dirección estrictamente en las ruedas traseras hay una clase de bicicletas con un punto de pivote en algún lugar entre las dos, conocida como dirección central, y similar a la dirección articulada . Una implementación temprana del concepto fue la bicicleta Phantom a principios de la década de 1870, promocionada como una alternativa más segura a la bicicleta de dos ruedas . [61] Este diseño permite una tracción delantera simple y las implementaciones actuales parecen ser bastante estables, incluso manejables sin manos, como ilustran muchas fotografías. [62] [63] Estos diseños, como la Python Lowracer, una reclinada, generalmente tienen ángulos de dirección muy laxos (40° a 65°) y un avance positivo o incluso negativo. El constructor de una bicicleta con avance negativo afirma que dirigir la bicicleta desde el frente obliga al asiento (y, por lo tanto, al ciclista) a elevarse ligeramente y esto compensa el efecto desestabilizador del avance negativo. [64]
Se han construido bicicletas, con fines de investigación y demostración, con la dirección invertida, de modo que al girar el manillar hacia la izquierda, la rueda delantera gira hacia la derecha, y viceversa. Es posible montar en una bicicleta de este tipo, pero a los ciclistas experimentados con bicicletas normales les resulta muy difícil aprender a hacerlo, si es que logran hacerlo. [65] [66]
El efecto timón es la expresión que se utiliza para describir cómo los manillares que se extienden mucho más allá del eje de dirección (tubo de dirección) actúan como un timón en un barco, en el que uno mueve las barras hacia la derecha para girar la rueda delantera hacia la izquierda, y viceversa. Esta situación se encuentra comúnmente en bicicletas cruiser , algunas reclinadas y algunas motocicletas. [67] Puede ser problemático cuando limita la capacidad de dirección debido a la interferencia o los límites del alcance del brazo. [68]
Los neumáticos tienen una gran influencia en el manejo de la motocicleta, especialmente en las motocicletas, [9] [45] pero también en las bicicletas. [7] [69] Los neumáticos influyen en la dinámica de la motocicleta de dos maneras distintas: radio de corona finito y generación de fuerza. Se ha demostrado que aumentar el radio de corona del neumático delantero disminuye el tamaño o elimina la autoestabilidad. Aumentar el radio de corona del neumático trasero tiene el efecto opuesto, pero en menor grado. [7]
Los neumáticos generan las fuerzas laterales necesarias para la dirección y el equilibrio a través de una combinación de fuerza en las curvas y empuje de inclinación . También se ha descubierto que las presiones de inflado de los neumáticos son variables importantes en el comportamiento de una motocicleta a altas velocidades. [70] Debido a que los neumáticos delanteros y traseros pueden tener diferentes ángulos de deslizamiento debido a la distribución del peso, las propiedades de los neumáticos, etc., las motos pueden experimentar subviraje o sobreviraje . De los dos, el subviraje, en el que la rueda delantera se desliza más que la trasera, es más peligroso ya que la dirección de la rueda delantera es fundamental para mantener el equilibrio. [9] Debido a que los neumáticos reales tienen un parche de contacto finito con la superficie de la carretera que puede generar un par de fricción, y cuando están en una curva, pueden experimentar cierto deslizamiento lateral a medida que ruedan, pueden generar pares sobre un eje normal al plano del parche de contacto.

Un par generado por un neumático, llamado par de autoalineación , es causado por asimetrías en el deslizamiento lateral a lo largo de la superficie de contacto. La fuerza resultante de este deslizamiento lateral se produce detrás del centro geométrico de la superficie de contacto, una distancia descrita como la pista neumática , y por lo tanto crea un par en el neumático. Dado que la dirección del deslizamiento lateral es hacia el exterior de la curva, la fuerza sobre el neumático es hacia el centro de la curva. Por lo tanto, este par tiende a girar la rueda delantera en la dirección del deslizamiento lateral, alejándose de la dirección de la curva y, por lo tanto, tiende a aumentar el radio de la curva.
Otro par motor se produce por el ancho finito de la superficie de contacto y la inclinación del neumático en una curva. La parte de la superficie de contacto que está hacia el exterior de la curva se mueve hacia atrás, con respecto al cubo de la rueda, más rápido que el resto de la superficie de contacto, debido a su mayor radio desde el cubo. Por el mismo razonamiento, la parte interior se mueve hacia atrás más lentamente. Por lo tanto, las partes exterior e interior de la superficie de contacto se deslizan sobre el pavimento en direcciones opuestas, lo que genera un par motor que tiende a girar la rueda delantera en la dirección de la curva y, por lo tanto, tiende a disminuir el radio de giro.
La combinación de estos dos pares opuestos crea un par de giro resultante en la rueda delantera, y su dirección es una función del ángulo de deslizamiento lateral del neumático, el ángulo entre la trayectoria real del neumático y la dirección a la que apunta, y el ángulo de inclinación del neumático (el ángulo en el que el neumático se inclina respecto de la vertical). [9] El resultado de este par es a menudo la supresión de la velocidad de inversión predicha por los modelos de ruedas rígidas descritos anteriormente en la sección sobre giro en estado estable. [11]
Un highsider es un tipo de movimiento de la bicicleta que se produce cuando una rueda trasera gana tracción cuando no está orientada en la dirección de viaje, generalmente después de deslizarse hacia un lado en una curva. [9] Esto puede ocurrir bajo un frenado fuerte, una aceleración, una superficie de la carretera variable o la activación de la suspensión, especialmente debido a la interacción con el tren de transmisión. [71] Puede tomar la forma de un solo deslizamiento y luego giro o una serie de oscilaciones violentas. [45]
La maniobrabilidad y el manejo de una bicicleta son difíciles de cuantificar por varias razones. La geometría de una bicicleta, especialmente el ángulo del eje de dirección, hace que el análisis cinemático sea complicado. [2] En muchas condiciones, las bicicletas son inherentemente inestables y siempre deben estar bajo el control del ciclista. Por último, la habilidad del ciclista tiene una gran influencia en el rendimiento de la bicicleta en cualquier maniobra. [9] Los diseños de bicicletas tienden a consistir en un equilibrio entre maniobrabilidad y estabilidad.

El control principal que puede realizar el ciclista es aplicar un par directamente al mecanismo de dirección a través del manillar. Debido a la dinámica propia de la bicicleta, a la geometría de la dirección y a los efectos giroscópicos, se ha descubierto que el control directo de la posición sobre el ángulo de dirección es problemático. [8]
Una entrada de control secundaria que el conductor puede hacer es inclinar el torso superior en relación con la motocicleta. Como se mencionó anteriormente, la efectividad de la inclinación del conductor varía inversamente con la masa de la motocicleta. En motocicletas pesadas, como las motocicletas, la inclinación del conductor altera principalmente los requisitos de distancia al suelo en una curva, mejora la vista de la carretera y mejora la dinámica del sistema de la motocicleta de una manera pasiva de muy baja frecuencia. [8] En las carreras de motocicletas, inclinar el torso, mover el cuerpo y proyectar una rodilla hacia el interior de la curva en relación con la motocicleta también puede causar un momento de guiñada aerodinámico que facilita la entrada y la vuelta en la curva. [9]
La necesidad de mantener la motocicleta en posición vertical para evitar lesiones al conductor y daños al vehículo limita el tipo de pruebas de maniobrabilidad que se realizan comúnmente. Por ejemplo, mientras que las publicaciones para aficionados a los automóviles suelen realizar y citar resultados de pistas de derrape , las publicaciones sobre motocicletas no lo hacen. La necesidad de "prepararse" para un giro, inclinar la motocicleta hasta el ángulo adecuado, significa que el conductor debe ver más allá de lo necesario para un automóvil típico a la misma velocidad, y esta necesidad aumenta más que en proporción a la velocidad. [8]
Se han ideado varios esquemas para evaluar el manejo de las bicicletas, particularmente de las motocicletas. [9]
Aunque sus ecuaciones de movimiento se pueden linealizar, una bicicleta es un sistema no lineal . La(s) variable(s) que se deben resolver no se pueden escribir como una suma lineal de componentes independientes, es decir, su comportamiento no se puede expresar como una suma de los comportamientos de sus descriptores. [2] En general, los sistemas no lineales son difíciles de resolver y son mucho menos comprensibles que los sistemas lineales. En el caso idealizado, en el que se ignora la fricción y cualquier flexión, una bicicleta es un sistema conservador . Sin embargo, la amortiguación aún se puede demostrar: en las circunstancias adecuadas, las oscilaciones de lado a lado disminuirán con el tiempo. La energía agregada con una sacudida lateral a una bicicleta que corre recta y en posición vertical (demostrando autoestabilidad) se convierte en una mayor velocidad de avance, no se pierde, a medida que las oscilaciones se extinguen. [2]
Una bicicleta es un sistema no holonómico porque su resultado depende de la trayectoria . Para conocer su configuración exacta, especialmente su ubicación, es necesario conocer no solo la configuración de sus partes, sino también sus historias: cómo se han movido a lo largo del tiempo. Esto complica el análisis matemático. [48] Finalmente, en el lenguaje de la teoría de control , una bicicleta exhibe un comportamiento de fase no mínima . [74] Gira en la dirección opuesta a la dirección en la que se dirige inicialmente, como se describió anteriormente en la sección sobre contradirección.
El número de grados de libertad de una bicicleta depende del modelo particular que se utilice. El modelo más simple que captura las características dinámicas clave, llamado "modelo Whipple" en honor a Francis Whipple, quien desarrolló por primera vez las ecuaciones para él, [2] tiene cuatro cuerpos rígidos con ruedas con filo de cuchillo que ruedan sin resbalar sobre una superficie plana y lisa, y tiene 7 grados de libertad (variables de configuración necesarias para describir completamente la ubicación y orientación de los 4 cuerpos): [2]
Las ecuaciones de movimiento de una bicicleta idealizada, que consisten en
puede representarse mediante una única ecuación diferencial ordinaria linealizada de cuarto orden o dos ecuaciones diferenciales de segundo orden acopladas, [2] la ecuación lean
y la ecuación de dirección
dónde
Estos se pueden representar en forma matricial como
dónde
En este modelo idealizado y linealizado, hay muchos parámetros geométricos (distancia entre ejes, ángulo de dirección, masa de cada cuerpo, radio de las ruedas, etc.), pero sólo cuatro variables significativas: ángulo de inclinación, tasa de inclinación, ángulo de dirección y tasa de dirección. Estas ecuaciones se han verificado mediante comparación con múltiples modelos numéricos derivados de forma completamente independiente. [2]
Las ecuaciones muestran que la bicicleta es como un péndulo invertido con la posición lateral de su soporte controlada por términos que representan la aceleración del balanceo, la velocidad del balanceo y el desplazamiento del balanceo en relación con la retroalimentación del par de dirección. El término de aceleración del balanceo normalmente tiene un signo incorrecto para la autoestabilización y se puede esperar que sea importante principalmente con respecto a las oscilaciones de bamboleo. La retroalimentación de la velocidad del balanceo tiene un signo correcto, es giroscópica por naturaleza, es proporcional a la velocidad y está dominada por la contribución de la rueda delantera. El término de desplazamiento del balanceo es el más importante y está controlado principalmente por el avance, la inclinación de la dirección y el desplazamiento del centro de masa del cuadro delantero con respecto al eje de dirección. Todos los términos implican combinaciones complejas de parámetros de diseño de la bicicleta y, a veces, la velocidad. Se consideran las limitaciones de la bicicleta de referencia y se incluyen extensiones a los tratamientos de neumáticos, cuadros y ciclistas [75] y sus implicaciones. También se discuten los controles óptimos del ciclista para la estabilización y el control de seguimiento de la trayectoria [7] .

Es posible calcular valores propios , uno para cada una de las cuatro variables de estado (ángulo de inclinación, tasa de inclinación, ángulo de dirección y tasa de dirección), a partir de las ecuaciones linealizadas para analizar los modos normales y la autoestabilidad de un diseño de bicicleta en particular. En el gráfico de la derecha, se calculan los valores propios de una bicicleta en particular para velocidades de avance de 0 a 10 m/s (22 mph). Cuando las partes reales de todos los valores propios (mostradas en azul oscuro) son negativas, la bicicleta es autoestable. Cuando las partes imaginarias de cualquier valor propio (mostradas en cian) no son cero, la bicicleta exhibe oscilación . Los valores propios son simétricos respecto del origen y, por lo tanto, cualquier diseño de bicicleta con una región autoestable en velocidades de avance no será autoestable yendo hacia atrás a la misma velocidad. [2]
Hay tres velocidades de avance que se pueden identificar en el gráfico de la derecha en las que el movimiento de la bicicleta cambia cualitativamente: [2]
Entre estas dos últimas velocidades, si ambas existen, hay un rango de velocidades de avance en el que el diseño particular de la bicicleta es autoestable. En el caso de la bicicleta cuyos valores propios se muestran aquí, el rango autoestable es de 5,3 a 8,0 m/s (12 a 18 mph). El cuarto valor propio, que suele ser estable (muy negativo), representa el comportamiento de avance de la rueda delantera, ya que tiende a girar hacia la dirección en la que se desplaza la bicicleta. Nótese que este modelo idealizado no presenta las inestabilidades de bamboleo o vibración y bamboleo trasero descritas anteriormente. Se observan en modelos que incorporan la interacción de los neumáticos con el suelo u otros grados de libertad. [9]
Los experimentos con bicicletas reales han confirmado hasta ahora el modo de oscilación predicho por los valores propios. Se descubrió que el deslizamiento de los neumáticos y la flexión del cuadro no son importantes para la dinámica lateral de la bicicleta en el rango de velocidad de hasta 6 m/s. [76]
Las bicicletas, como mecanismos complejos, tienen una variedad de modos : formas fundamentales en las que pueden moverse. Estos modos pueden ser estables o inestables, dependiendo de los parámetros de la bicicleta y su velocidad de avance. En este contexto, "estable" significa que una bicicleta no controlada continuará rodando hacia adelante sin caerse mientras se mantenga la velocidad de avance. Por el contrario, "inestable" significa que una bicicleta no controlada eventualmente se caerá, incluso si se mantiene la velocidad de avance. Los modos se pueden diferenciar por la velocidad a la que cambian la estabilidad y las fases relativas de inclinación y dirección a medida que la bicicleta experimenta ese modo. Cualquier movimiento de bicicleta consiste en una combinación de varias cantidades de los modos posibles, y hay tres modos principales que una bicicleta puede experimentar: vuelco, oscilación y tambaleo. [2] Un modo menos conocido es el tambaleo trasero, y generalmente es estable. [9]
El vuelco es una caída sin oscilación. Durante el vuelco, una rueda delantera descontrolada suele girar en la dirección de la inclinación, pero nunca lo suficiente como para detener la inclinación creciente, hasta que se alcanza un ángulo de inclinación muy alto, momento en el que la dirección puede girar en la dirección opuesta. Un vuelco puede ocurrir muy lentamente si la motocicleta avanza rápidamente. Debido a que la inestabilidad del vuelco es tan lenta, del orden de segundos, es fácil para el conductor controlarla y, de hecho, la utiliza para iniciar la inclinación necesaria para un giro. [9] Para la mayoría de las motocicletas, dependiendo de la geometría y la distribución de la masa, el vuelco es estable a bajas velocidades y se vuelve menos estable a medida que aumenta la velocidad hasta que ya no es estable. Sin embargo, en muchas motocicletas, la interacción de los neumáticos con el pavimento es suficiente para evitar que el vuelco se vuelva inestable a altas velocidades. [9] [11]
El movimiento de balanceo es una oscilación lenta (0&–4&–Hz) entre la inclinación hacia la izquierda y la dirección hacia la derecha, y viceversa. Toda la motocicleta se ve afectada con cambios significativos en el ángulo de dirección, el ángulo de inclinación (balanceo) y el ángulo de rumbo (guiñada). La dirección está desfasada 180° con respecto al rumbo y 90° con respecto a la inclinación. [9] Esta película AVI muestra el movimiento de balanceo.
En la mayoría de las bicicletas, dependiendo de la geometría y la distribución de la masa, el movimiento es inestable a bajas velocidades y se vuelve menos pronunciado a medida que aumenta la velocidad hasta que deja de ser inestable. Si bien la amplitud puede disminuir, la frecuencia en realidad aumenta con la velocidad. [15]
Los términos " bamboleo " , "slapper" , "speed wobble" y "mortal wobble" son todos términos y frases que se utilizan para describir una oscilación rápida (4–10 Hz) de principalmente la parte delantera (rueda delantera, horquilla y manillar). También está implicada la oscilación del cuadro trasero, que puede contribuir al bamboleo cuando es demasiado flexible. [77] Esta inestabilidad se produce principalmente a alta velocidad y es similar a la que experimentan las ruedas de los carros de la compra, el tren de aterrizaje de los aviones y las ruedas delanteras de los automóviles. [9] [11] Aunque el bamboleo o el bamboleo se pueden remediar fácilmente ajustando la velocidad, la posición o el agarre del manillar, puede ser fatal si no se controla. [78]
El bamboleo o vibración comienza cuando alguna irregularidad menor, como la asimetría de la horquilla, [79] acelera la rueda hacia un lado. La fuerza de recuperación se aplica en fase con el progreso de la irregularidad y la rueda gira hacia el otro lado, donde se repite el proceso. Si no hay suficiente amortiguación en la dirección, la oscilación aumentará hasta que se produzca un fallo del sistema. La frecuencia de oscilación se puede cambiar modificando la velocidad de avance, haciendo que la bicicleta sea más rígida o más ligera, o aumentando la rigidez de la dirección, de la que el ciclista es un componente principal. [16] [28]
El término bamboleo trasero se utiliza para describir un modo de oscilación en el que el ángulo de inclinación (balanceo) y el ángulo de dirección (guiñada) están casi en fase y ambos están desfasados 180° con respecto al ángulo de dirección. La frecuencia de esta oscilación es moderada, con un máximo de unos 6,5 Hz. El bamboleo trasero está muy amortiguado y disminuye rápidamente a medida que aumenta la velocidad de la motocicleta. [9]
El efecto que los parámetros de diseño de una bicicleta tienen sobre estos modos se puede investigar examinando los valores propios de las ecuaciones de movimiento linealizadas. [70] Para más detalles sobre las ecuaciones de movimiento y los valores propios, véase la sección sobre las ecuaciones de movimiento anterior. Aquí se describen algunas conclusiones generales que se han extraído.
La rigidez lateral y torsional del bastidor trasero y del eje de la rueda afecta sustancialmente a la amortiguación en modo oscilante. Se ha descubierto que una distancia entre ejes y un avance largos y un ángulo de dirección plano aumentan la amortiguación en modo oscilante. La distorsión lateral se puede contrarrestar ubicando el eje de torsión de la horquilla delantera lo más bajo posible.
Las tendencias a la oscilación en las curvas se ven amplificadas por una amortiguación degradada de la suspensión trasera . La rigidez en las curvas, la inclinación y la longitud de relajación del neumático trasero son los factores que más contribuyen a la amortiguación de la oscilación. Los mismos parámetros del neumático delantero tienen un efecto menor. La carga trasera también amplifica las tendencias a la oscilación en las curvas. Sin embargo, los conjuntos de carga trasera con la rigidez y la amortiguación adecuadas lograron amortiguar las oscilaciones de oscilación y bamboleo.
Un estudio ha demostrado teóricamente que, mientras una bicicleta se inclina en una curva, las ondulaciones de la carretera pueden excitar el modo de oscilación a alta velocidad o el modo de tambaleo a baja velocidad si cualquiera de sus frecuencias coincide con la velocidad del vehículo y otros parámetros. La excitación del modo de tambaleo se puede mitigar con un amortiguador de dirección eficaz y la excitación del modo de oscilación es peor para los ciclistas ligeros que para los ciclistas pesados. [14]
Andar en una cinta de correr es teóricamente idéntico a andar en pavimento fijo, y pruebas físicas lo han confirmado. [80] Se han desarrollado cintas de correr específicamente para el entrenamiento en bicicleta en interiores. [81] [82] El andar en rodillos todavía está bajo investigación. [83] [84] [85]
Aunque las bicicletas y las motocicletas pueden parecer mecanismos simples con solo cuatro partes móviles principales (marco, horquilla y dos ruedas), estas partes están dispuestas de una manera que las hace complicadas de analizar. [28] Si bien es un hecho observable que las bicicletas se pueden montar incluso cuando se cancelan los efectos giroscópicos de sus ruedas, [5] [6] la hipótesis de que los efectos giroscópicos de las ruedas son lo que mantiene a una bicicleta en posición vertical es común en la prensa escrita y en línea. [5] [48]
Ejemplos impresos:

Las bicicletas pueden experimentar una variedad de fuerzas y movimientos longitudinales. En la mayoría de las bicicletas, cuando la rueda delantera se gira hacia un lado o hacia el otro, todo el cuadro trasero se inclina ligeramente hacia adelante, dependiendo del ángulo del eje de dirección y la cantidad de recorrido. [9] [47] En las bicicletas con suspensiones, ya sea delantera, trasera o ambas, el ajuste se utiliza para describir la configuración geométrica de la bicicleta, especialmente en respuesta a las fuerzas de frenado, aceleración, giro, transmisión y resistencia aerodinámica. [9]
La carga soportada por las dos ruedas varía no solo con la ubicación del centro de masa, que a su vez varía con el número de pasajeros, la cantidad de equipaje y la ubicación de los pasajeros y el equipaje, sino también con la aceleración y la desaceleración. Este fenómeno se conoce como transferencia de carga [9] o transferencia de peso [45] [71] según el autor, y presenta desafíos y oportunidades tanto para los conductores como para los diseñadores. Por ejemplo, los corredores de motocicletas pueden usarlo para aumentar la fricción disponible para el neumático delantero al tomar curvas, y los intentos de reducir la compresión de la suspensión delantera durante un frenado fuerte han generado varios diseños de horquillas para motocicletas .
Se puede considerar que las fuerzas de arrastre aerodinámicas netas actúan en un único punto, llamado centro de presión . [45] A altas velocidades, esto creará un momento neto alrededor de la rueda motriz trasera y dará como resultado una transferencia neta de carga de la rueda delantera a la rueda trasera. [45] Además, dependiendo de la forma de la motocicleta y la forma de cualquier carenado que pueda instalarse, puede haber una elevación aerodinámica que aumente o reduzca aún más la carga en la rueda delantera. [45]
Aunque una bicicleta es longitudinalmente estable cuando está parada, puede volverse longitudinalmente inestable bajo suficiente aceleración o desaceleración, y la segunda ley de Euler se puede utilizar para analizar las fuerzas de reacción del suelo generadas. [86] Por ejemplo, las fuerzas de reacción del suelo normales (verticales) en las ruedas de una bicicleta con una distancia entre ejes y un centro de masa a una altura y una distancia frente al eje de la rueda trasera, y para simplificar, con ambas ruedas bloqueadas, se pueden expresar como: [9]
Las fuerzas de fricción (horizontales) son simplemente
donde es el coeficiente de fricción , es la masa total de la bicicleta y el ciclista, y es la aceleración de la gravedad. Por lo tanto, si
que ocurre si el centro de masa está en cualquier lugar por encima o delante de una línea que se extiende hacia atrás desde el área de contacto de la rueda delantera e inclinada en el ángulo
por encima de la horizontal, [45] entonces la fuerza normal de la rueda trasera será cero (en cuyo punto la ecuación ya no se aplica) y la bicicleta comenzará a voltearse o girar hacia adelante sobre la rueda delantera.
Por otro lado, si la altura del centro de masas está detrás o debajo de la línea, como en la mayoría de las bicicletas tándem o bicicletas reclinadas de larga distancia entre ejes, así como en los automóviles , es menos probable que la rueda delantera pueda generar suficiente fuerza de frenado para volcar la bicicleta. Esto significa que pueden desacelerar hasta casi el límite de adherencia de los neumáticos a la carretera, que podría alcanzar 0,8 g si el coeficiente de fricción es 0,8, que es un 40% más que una bicicleta vertical incluso en las mejores condiciones. El autor de Bicycling Science, David Gordon Wilson, señala que esto pone a los ciclistas erguidos en particular riesgo de causar una colisión trasera si van demasiado cerca de los automóviles. [87]
De manera similar, las motocicletas potentes pueden generar suficiente torque en la rueda trasera para levantar la rueda delantera del suelo en una maniobra llamada caballito . Se puede trazar una línea similar a la descrita anteriormente para analizar el rendimiento de frenado a partir de la zona de contacto de la rueda trasera para predecir si es posible un caballito dada la fricción disponible, la ubicación del centro de masa y la potencia suficiente. [45] Esto también puede suceder en las bicicletas, aunque hay mucha menos potencia disponible, si el centro de masa está atrás o lo suficientemente arriba o el ciclista se tambalea hacia atrás al aplicar potencia a los pedales. [88]
Por supuesto, el ángulo del terreno puede influir en todos los cálculos anteriores. Si todo lo demás permanece igual, el riesgo de volcar la parte delantera se reduce al subir una pendiente y aumenta al bajarla. La posibilidad de hacer un caballito aumenta al subir una pendiente [88] y es un factor importante en las competiciones de motociclismo de montaña .

Al frenar, el ciclista en movimiento busca cambiar la velocidad de la masa combinada m del ciclista más la bicicleta. Esta es una aceleración negativa a en la línea de desplazamiento. F = ma , la aceleración a provoca una fuerza inercial hacia adelante F sobre la masa m . El frenado a se produce desde una velocidad inicial u hasta una velocidad final v , durante un período de tiempo t . La ecuación u - v = at implica que cuanto mayor sea la aceleración, menor será el tiempo necesario para cambiar la velocidad. La distancia de frenado s también es más corta cuando la aceleración a está en el valor más alto posible compatible con las condiciones de la carretera: la ecuación s = ut + 1/2 at 2 hace que s sea baja cuando a es alta y t es baja.
La cantidad de fuerza de frenado que se debe aplicar a cada rueda depende tanto de las condiciones del terreno como del equilibrio de peso sobre las ruedas en cada instante. La fuerza de frenado total no puede superar la fuerza de gravedad sobre el ciclista y la bicicleta multiplicada por el coeficiente de fricción μ del neumático sobre el suelo. mgμ >= Ff + Fr . Se produce un derrape si la relación entre Ff y Nf o entre Fr y Nr es mayor que μ , y el derrape de la rueda trasera tiene un impacto negativo menor en la estabilidad lateral.
Al frenar, la fuerza inercial ma en la línea de desplazamiento, al no ser colineal con f , tiende a girar m alrededor de f . Esta tendencia a girar, un momento de vuelco, se ve resistida por un momento de mg .

Tomando momentos del punto de contacto de la rueda delantera en un instante determinado:

Otros factores:
Los valores de μ varían mucho dependiendo de varios factores:

La mayor parte de la fuerza de frenado de las bicicletas verticales estándar proviene de la rueda delantera. Como muestra el análisis anterior, si los frenos son lo suficientemente fuertes, la rueda trasera es fácil de derrapar, mientras que la rueda delantera a menudo puede generar suficiente fuerza de frenado para volcar al ciclista y la bicicleta sobre la rueda delantera. Esto se llama stoppie si la rueda trasera se levanta pero la bicicleta no se voltea, o endo (forma abreviada de end-over-end ) si la bicicleta se voltea. Sin embargo, en bicicletas largas o bajas, como las motocicletas cruiser [90] y las bicicletas reclinadas , el neumático delantero patinará en su lugar, lo que posiblemente cause una pérdida de equilibrio. Suponiendo que no haya pérdida de equilibrio, es posible calcular el rendimiento de frenado óptimo dependiendo de la geometría de la bicicleta, la ubicación del centro de gravedad de la bicicleta y el ciclista y el coeficiente máximo de fricción. [91]
En el caso de una suspensión delantera , especialmente en el caso de los tubos de horquilla telescópicos , el aumento de la fuerza descendente sobre la rueda delantera durante el frenado puede provocar que la suspensión se comprima y que la parte delantera baje. Esto se conoce como frenado por caída de la rueda . Una técnica de conducción que aprovecha la forma en que el frenado aumenta la fuerza descendente sobre la rueda delantera se conoce como frenado por caída .
Los factores limitantes de la desaceleración máxima en el frenado de la rueda delantera son:
En el caso de una bicicleta vertical sobre asfalto seco con frenos excelentes, el cabeceo probablemente será el factor limitante. El centro de masa combinado de una bicicleta vertical típica y el ciclista estará a unos 60 cm (24 pulgadas) detrás de la zona de contacto de la rueda delantera y 120 cm (47 pulgadas) por encima, lo que permite una desaceleración máxima de 0,5 g (5 m/s2 o 16 pies/s2 ) . [28] Sin embargo, si el ciclista modula los frenos correctamente, se puede evitar el cabeceo. Si el ciclista mueve su peso hacia atrás y hacia abajo, son posibles desaceleraciones aún mayores.
El freno trasero de una bicicleta vertical solo puede producir una desaceleración de aproximadamente 0,25 g (≈2,5 m/s 2 ) en el mejor de los casos, [87] debido a la disminución de la fuerza normal en la rueda trasera como se describió anteriormente. Todas las bicicletas de este tipo con solo freno trasero están sujetas a esta limitación: por ejemplo, las bicicletas con solo un freno de contrapedal y las bicicletas de piñón fijo sin otro mecanismo de frenado. Sin embargo, existen situaciones que pueden justificar el frenado de la rueda trasera [93]
La opinión de los expertos varía desde "utilizar ambas palancas por igual al principio" [95] hasta "lo más rápido que puedes detener cualquier motocicleta con una distancia entre ejes normal es aplicar el freno delantero con tanta fuerza que la rueda trasera esté a punto de levantarse del suelo", [93] dependiendo de las condiciones de la carretera, el nivel de habilidad del ciclista y la fracción deseada de la desaceleración máxima posible.
El sistema SureStop utiliza un mecanismo deslizante que permite que los frenos delanteros se accionen mediante la fricción que se aplica a las zapatas de freno traseras al girar la rueda trasera. Esto está diseñado para optimizar la fricción de frenado en función de las condiciones de la carretera y así mitigar el riesgo de salirse del manillar.

Las bicicletas pueden tener solo suspensión delantera, solo trasera, suspensión total o ninguna suspensión que funcione principalmente en el plano central de simetría; aunque con cierta consideración por la flexibilidad lateral. [45] Los objetivos de la suspensión de una bicicleta son reducir la vibración experimentada por el ciclista, mantener el contacto de la rueda con el suelo, reducir la pérdida de impulso al pasar sobre un objeto, reducir las fuerzas de impacto causadas por saltos o caídas y mantener el equilibrio del vehículo. [9] Los parámetros principales de la suspensión son la rigidez , la amortiguación , la masa suspendida y no suspendida y las características de los neumáticos . [45]
El estudio de las vibraciones en las bicicletas incluye sus causas, como el equilibrio del motor , [96] el equilibrio de las ruedas , la superficie del suelo y la aerodinámica ; su transmisión y absorción; y sus efectos en la bicicleta, el ciclista y la seguridad. [97] Un factor importante en cualquier análisis de vibraciones es una comparación de las frecuencias naturales del sistema con las posibles frecuencias de conducción de las fuentes de vibración. [98] Una coincidencia cercana significa resonancia mecánica que puede resultar en grandes amplitudes . Un desafío en la amortiguación de vibraciones es crear cumplimiento en ciertas direcciones (verticalmente) sin sacrificar la rigidez del marco necesaria para la transmisión de potencia y el manejo ( torsionalmente ). [99] Otro problema con la vibración para la bicicleta es la posibilidad de falla debido a la fatiga del material . [100] Los efectos de la vibración en los ciclistas incluyen incomodidad, pérdida de eficiencia, síndrome de vibración mano-brazo , una forma secundaria de la enfermedad de Raynaud y vibración de todo el cuerpo . Los instrumentos vibratorios pueden ser inexactos o difíciles de leer. [100]
La principal causa de las vibraciones en una bicicleta que funciona correctamente es la superficie sobre la que rueda. Además de los neumáticos y las suspensiones de bicicleta tradicionales , se han desarrollado diversas técnicas para amortiguar las vibraciones antes de que lleguen al ciclista. Estas incluyen materiales, como la fibra de carbono , ya sea en todo el cuadro o solo en componentes clave como la horquilla delantera , la tija del sillín o el manillar ; formas de tubo, como tirantes de asiento curvados ; [101] puños y sillines de manillar de gel e insertos especiales, como Zertz de Specialized , [102] [103] y Buzzkills de Bontrager .
Además de la superficie de la carretera, las vibraciones en una motocicleta pueden ser causadas por el motor y las ruedas, si están desequilibradas. Los fabricantes emplean una variedad de tecnologías para reducir o amortiguar estas vibraciones, como ejes de equilibrio del motor , soportes de motor de goma, [104] y pesos para neumáticos . [105] Los problemas que causa la vibración también han generado una industria de piezas y sistemas de posventa diseñados para reducirla. Los complementos incluyen pesos de manillar , [106] estriberas aisladas y contrapesos del motor . A altas velocidades, las motocicletas y sus conductores también pueden experimentar vibraciones o sacudidas aerodinámicas . [107] Esto se puede reducir cambiando el flujo de aire sobre piezas clave, como el parabrisas . [108]
Una variedad de experimentos verifican o refutan varias hipótesis sobre la dinámica de la bicicleta.
una sola vía es más difícil de estudiar que el automóvil de doble vía y plantea un desafío para el dinamizador de vehículos.
Existen algunos conceptos erróneos sobre la estabilidad de la bicicleta.
Amortiguador de dirección para bicicleta, totalmente hidráulico, de 140 gramos
Las correcciones de dirección afectan a una carga delantera más directamente que a una carga trasera. Esto significa que equilibrar una carga delantera requiere correcciones de dirección más pequeñas.
Comenzaré simplemente diciendo que la forma de aumentar la estabilidad de una bicicleta es aumentar la T (recorrido de la horquilla).
En lo que respecta al primer vehículo de calle, es evidente un notable comportamiento de sobreviraje; ..., y por lo tanto la conducción se lleva a cabo utilizando un cierto ángulo de contraviraje.
Las correlaciones con las opiniones subjetivas de los conductores de pruebas expertos han demostrado que se debe aplicar un esfuerzo de torsión bajo al manillar para tener una buena sensación, y preferiblemente en un sentido opuesto a la dirección de giro.
El esfuerzo físico de dirección necesario para mantener el equilibrio no es demasiado grande, pero el esfuerzo mental y la velocidad de reacción necesarios para andar en bicicleta a alta velocidad son muy altos.[ aclaración necesaria ]
lo tanto, concluimos que andar en bicicleta en una cinta de correr con una velocidad de banda constante es dinámicamente equivalente a andar en bicicleta en un terreno plano y nivelado en la dirección recta hacia adelante con velocidad constante.
Algunas motocicletas simplemente no pueden, en condiciones normales, hacer un Stoppie. Las GoldWings y la mayoría de las Harley-Davidson, por ejemplo. Antes de que se produzca un Stoppie, se debe lavar la parte delantera.
El frenado máximo se produce cuando se aplica el freno delantero con tanta fuerza que la rueda trasera está a punto de despegarse. En general, desaconsejo utilizar ambos frenos al mismo tiempo.
por igual al principio.
Vídeos :
Centros de investigación :
Conferencias :