

En matemáticas , el teorema de los cuatro colores , o teorema del mapa de los cuatro colores , establece que no se requieren más de cuatro colores para colorear las regiones de cualquier mapa, de modo que no haya dos regiones adyacentes que tengan el mismo color. Adyacente significa que dos regiones comparten un límite común de longitud distinta de cero (es decir, no simplemente una esquina donde se encuentran tres o más regiones). [1] Fue el primer teorema importante demostrado utilizando una computadora . Inicialmente, esta prueba no fue aceptada por todos los matemáticos porque la prueba asistida por computadora no era factible de verificar a mano por un humano . [2] La prueba ha ganado amplia aceptación desde entonces, aunque persisten algunas dudas. [3]
El teorema es una versión más sólida del teorema de los cinco colores , que se puede demostrar mediante un argumento significativamente más simple. Aunque el teorema de los cinco colores más débiles ya se demostró en el siglo XIX, el teorema de los cuatro colores resistió hasta 1976, cuando fue demostrado por Kenneth Appel y Wolfgang Haken . Esto se produjo después de muchas pruebas falsas y contraejemplos erróneos en las décadas anteriores.
La prueba de Appel-Haken procede analizando un gran número de configuraciones reducibles. Esto fue mejorado en 1997 por Robertson, Sanders, Seymour y Thomas, quienes lograron disminuir el número de tales configuraciones a 633, lo que sigue siendo un análisis de casos extremadamente largo. En 2005, Georges Gonthier verificó el teorema utilizando un software de demostración de teoremas de uso general .
En términos de teoría de grafos, el teorema establece que para un gráfico plano sin bucles , su número cromático es .
La afirmación intuitiva del teorema de los cuatro colores – "dada cualquier separación de un plano en regiones contiguas, las regiones se pueden colorear usando como máximo cuatro colores de modo que no haya dos regiones adyacentes que tengan el mismo color" – debe interpretarse apropiadamente para que sea correcta. .
Primero, las regiones son adyacentes si comparten un segmento límite; dos regiones que comparten sólo puntos límite aislados no se consideran adyacentes. (De lo contrario, un mapa en forma de gráfico circular haría que un número arbitrariamente grande de regiones fueran "adyacentes" entre sí en una esquina común y, como resultado, requeriría un número arbitrariamente grande de colores). En segundo lugar, regiones extrañas, como aquellos con área finita pero perímetro infinitamente largo, no están permitidos; Los mapas con tales regiones pueden requerir más de cuatro colores. [4] (Para estar seguros, podemos restringirnos a regiones cuyos límites constan de un número finito de segmentos de línea recta. Se permite que una región tenga enclaves , es decir, rodee por completo a una o más regiones). Tenga en cuenta que la noción de " región contigua" (técnicamente: subconjunto abierto conectado del avión) no es lo mismo que la de un "país" en mapas regulares, ya que los países no necesitan ser contiguos (pueden tener enclaves , por ejemplo, la provincia de Cabinda como parte de Angola , Najicheván como parte de Azerbaiyán , Kaliningrado como parte de Rusia, Francia con sus territorios de ultramar y Alaska como parte de Estados Unidos no son contiguos). Si exigimos que todo el territorio de un país reciba el mismo color, entonces cuatro colores no siempre son suficientes. Por ejemplo, considere un mapa simplificado:

En este mapa, las dos regiones etiquetadas como A pertenecen al mismo país. Si quisiéramos que esas regiones recibieran el mismo color, entonces se necesitarían cinco colores, ya que las dos regiones A juntas son adyacentes a otras cuatro regiones, cada una de las cuales es adyacente a todas las demás. Se puede forzar que dos regiones separadas tengan el mismo color agregando un "asa" que las una fuera del plano.

Tal construcción hace que el problema sea equivalente a colorear un mapa en un toro (una superficie del género 1), lo que requiere hasta 7 colores para un mapa arbitrario. También se aplica una construcción similar si se utiliza un solo color para múltiples áreas separadas, como para masas de agua en mapas reales, o si hay más países con territorios separados. En tales casos, es posible que se requieran más colores con un género creciente de superficie resultante. (Consulte la sección Generalizaciones a continuación).
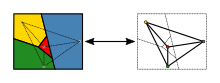
Un enunciado más simple del teorema utiliza la teoría de grafos . El conjunto de regiones de un mapa se puede representar de manera más abstracta como un gráfico no dirigido que tiene un vértice para cada región y un borde para cada par de regiones que comparten un segmento límite. Este gráfico es plano : se puede dibujar en el plano sin cruces colocando cada vértice en una ubicación elegida arbitrariamente dentro de la región a la que corresponde, y dibujando los bordes como curvas sin cruces que van desde el vértice de una región, a través de una región compartida. segmento límite, al vértice de una región adyacente. Por el contrario, de esta manera se puede formar cualquier gráfico plano a partir de un mapa. En terminología de teoría de grafos, el teorema de los cuatro colores establece que los vértices de cada gráfico plano se pueden colorear con como máximo cuatro colores, de modo que dos vértices adyacentes no reciban el mismo color, o para abreviar:

Hasta donde se sabe, [6] la conjetura fue propuesta por primera vez el 23 de octubre de 1852, [7] cuando Francis Guthrie , mientras intentaba colorear el mapa de los condados de Inglaterra, notó que sólo se necesitaban cuatro colores diferentes. En ese momento, el hermano de Guthrie, Frederick , era alumno de Augustus De Morgan (el ex asesor de Francis) en el University College de Londres . Francis preguntó a Frederick al respecto, quien luego se lo llevó a De Morgan (Francis Guthrie se graduó más tarde en 1852 y luego se convirtió en profesor de matemáticas en Sudáfrica). Según De Morgan:
Un estudiante mío [Guthrie] me pidió hoy que le diera una razón para un hecho que no sabía que era un hecho, y todavía no lo sé. Dice que si una figura está dividida de cualquier manera y los compartimentos tienen colores diferentes, de modo que las figuras con cualquier porción de línea límite común tienen colores diferentes (pueden ser necesarios cuatro colores, pero no más), el siguiente es su caso en el que se necesitan cuatro colores. No se puede inventar una consulta que sea necesaria para cinco o más… [8] [ página necesaria ]
"FG", quizás uno de los dos Guthrie, publicó la pregunta en The Athenaeum en 1854, [9] y De Morgan volvió a plantear la pregunta en la misma revista en 1860. [10] Otra referencia temprana publicada por Arthur Cayley (1879) a su vez atribuye la conjetura a De Morgan.
Hubo varios intentos fallidos de demostrar el teorema. De Morgan creía que se derivaba de un hecho simple sobre cuatro regiones, aunque no creía que ese hecho pudiera derivarse de hechos más elementales.
Esto surge de la siguiente manera. Nunca necesitamos cuatro colores en un vecindario a menos que haya cuatro condados, cada uno de los cuales tenga líneas fronterizas en común con cada uno de los otros tres. Tal cosa no puede suceder con cuatro áreas a menos que una o más de ellas estén rodeadas por el resto; y el color utilizado para el condado cerrado queda así libre para continuar. Ahora bien, creemos plenamente que este principio de que cuatro áreas no pueden tener límites comunes con las otras tres sin un cierre, no es, creemos plenamente, capaz de demostrarse sobre algo más evidente y más elemental; debe permanecer como un postulado. [10]
Alfred Kempe presentó una prueba propuesta en 1879, que fue ampliamente aclamada; [11] Peter Guthrie Tait dio otro en 1880. No fue hasta 1890 que Percy Heawood demostró que la prueba de Kempe era incorrecta, y en 1891, Julius Petersen demostró que la prueba de Tait era incorrecta ; cada prueba falsa permaneció sin oposición durante 11 años. [12]
En 1890, además de exponer el defecto de la prueba de Kempe, Heawood demostró el teorema de los cinco colores y generalizó la conjetura de los cuatro colores a superficies de género arbitrario. [13]
Tait, en 1880, demostró que el teorema de los cuatro colores es equivalente a la afirmación de que cierto tipo de gráfico (llamado snark en la terminología moderna) debe ser no plano . [14]
En 1943, Hugo Hadwiger formuló la conjetura de Hadwiger , [15] una generalización de gran alcance del problema de los cuatro colores que aún permanece sin resolver.
Durante las décadas de 1960 y 1970, el matemático alemán Heinrich Heesch desarrolló métodos de uso de computadoras para buscar una prueba. En particular, fue el primero en utilizar la descarga para demostrar el teorema, lo que resultó ser importante en la parte de inevitabilidad de la posterior demostración de Appel-Haken. También amplió el concepto de reducibilidad y, junto con Ken Durre, desarrolló una prueba informática para ello. Desafortunadamente, en este momento crítico, no pudo conseguir el tiempo de supercomputadora necesario para continuar su trabajo. [8]
Otros adoptaron sus métodos, incluido su enfoque asistido por computadora. Mientras otros equipos de matemáticos corrían para completar las demostraciones, Kenneth Appel y Wolfgang Haken de la Universidad de Illinois anunciaron, el 21 de junio de 1976, [16] que habían demostrado el teorema. John A. Koch los ayudó en algunos trabajos algorítmicos. [8]
Si la conjetura de los cuatro colores fuera falsa, habría al menos un mapa con el menor número posible de regiones que requeriría cinco colores. La prueba demostró que un contraejemplo tan mínimo no puede existir, mediante el uso de dos conceptos técnicos: [17]
Utilizando reglas y procedimientos matemáticos basados en propiedades de configuraciones reducibles, Appel y Haken encontraron un conjunto inevitable de configuraciones reducibles, demostrando así que no podía existir un contraejemplo mínimo a la conjetura de los cuatro colores. Su prueba redujo la infinidad de mapas posibles a 1.834 configuraciones reducibles (luego reducidas a 1.482) que tuvieron que ser comprobadas una por una por computadora y requirieron más de mil horas. Esta parte de reducibilidad del trabajo se verificó dos veces de forma independiente con diferentes programas y computadoras. Sin embargo, la parte inevitable de la prueba se verificó en más de 400 páginas de microfichas , que tuvieron que ser revisadas a mano con la ayuda de la hija de Haken, Dorothea Blostein (Appel y Haken 1989).
El anuncio de Appel y Haken fue ampliamente difundido por los medios de comunicación de todo el mundo, y el departamento de matemáticas de la Universidad de Illinois utilizó un matasellos que decía "Cuatro colores son suficientes". Al mismo tiempo, la naturaleza inusual de la demostración (fue el primer teorema importante demostrado con amplia asistencia informática) y la complejidad de la parte verificable por humanos despertaron una controversia considerable. [8] [ página necesaria ]
A principios de la década de 1980, se difundieron rumores sobre un defecto en la prueba de Appel-Haken. Ulrich Schmidt, de la RWTH Aachen, examinó las pruebas de Appel y Haken para su tesis de maestría publicada en 1981. [8] [ página necesaria ] Comprobó alrededor del 40% de la parte de inevitabilidad y encontró un error significativo en el procedimiento de descarga (Appel & Haken 1989). En 1986, el editor de Mathematical Intelligencer pidió a Appel y Haken que escribieran un artículo abordando los rumores sobre fallas en su demostración. Respondieron que los rumores se debían a una "mala interpretación de los resultados [de Schmidt]" y le respondieron con un artículo detallado. [8] [ página necesaria ] Su obra maestra , Every Planar Map is Four-Colorable , un libro que afirma tener una prueba completa y detallada (con un suplemento de microfichas de más de 400 páginas), apareció en 1989; explicó y corrigió el error descubierto por Schmidt, así como varios errores adicionales encontrados por otros (Appel y Haken 1989).
Desde la demostración del teorema, un nuevo enfoque ha llevado a una prueba más corta y a un algoritmo más eficiente para mapas de 4 colores. En 1996, Neil Robertson , Daniel P. Sanders , Paul Seymour y Robin Thomas crearon un algoritmo de tiempo cuadrático (que requiere sólo tiempo O ( n 2 ), donde n es el número de vértices), mejorando un algoritmo de tiempo cuártico basado en sobre la prueba de Appel y Haken. [18] La nueva prueba, basada en las mismas ideas, es similar a la de Appel y Haken pero más eficiente porque reduce la complejidad del problema y requiere verificar solo 633 configuraciones reducibles. Tanto la parte de inevitabilidad como la de reducibilidad de esta nueva prueba deben ejecutarse por computadora y no es práctico verificarlas a mano. [19] En 2001, los mismos autores anunciaron una prueba alternativa, demostrando la conjetura de Snark . [20] Sin embargo, esta prueba permanece inédita.
En 2005, Benjamin Werner y Georges Gonthier formalizaron una demostración del teorema dentro del asistente de prueba de Coq . Esto eliminó la necesidad de confiar en los diversos programas informáticos utilizados para verificar casos particulares; sólo es necesario confiar en el núcleo Coq. [21]
La siguiente discusión es un resumen basado en la introducción a Every Planar Map is Four Colorable (Appel & Haken 1989). Aunque defectuosa, la supuesta demostración original de Kempe del teorema de los cuatro colores proporcionó algunas de las herramientas básicas utilizadas posteriormente para demostrarlo. La explicación aquí está reformulada en términos de la formulación anterior de la teoría de grafos moderna.
El argumento de Kempe es el siguiente. Primero, si las regiones planas separadas por el gráfico no están trianguladas , es decir, no tienen exactamente tres aristas en sus límites, podemos agregar aristas sin introducir nuevos vértices para hacer que cada región sea triangular, incluida la región exterior ilimitada. Si este gráfico triangulado se puede colorear usando cuatro colores o menos, también lo es el gráfico original, ya que la misma coloración es válida si se eliminan los bordes. Por lo tanto, basta con demostrar el teorema de los cuatro colores para gráficas trianguladas para demostrarlo para todas las gráficas planas, y sin pérdida de generalidad asumimos que la gráfica está triangulada.
Supongamos que v , e y f son el número de vértices, aristas y regiones (caras). Como cada región es triangular y cada arista es compartida por dos regiones, tenemos que 2 e = 3 f . Esto, junto con la fórmula de Euler , v − e + f = 2, se puede usar para demostrar que 6 v − 2 e = 12. Ahora, el grado de un vértice es el número de aristas que lo lindan. Si v n es el número de vértices de grado n y D es el grado máximo de cualquier vértice,
Pero como 12 > 0 y 6 − i ≤ 0 para todo i ≥ 6, esto demuestra que hay al menos un vértice de grado 5 o menos.
Si hay un gráfico que requiere 5 colores, entonces existe un gráfico mínimo , donde la eliminación de cualquier vértice lo convierte en cuatro colores. Llame a este gráfico G . Entonces G no puede tener un vértice de grado 3 o menos, porque si d ( v ) ≤ 3, podemos eliminar v de G , pintar en cuatro colores el gráfico más pequeño, luego volver a agregar v y extenderle los cuatro colores eligiendo un color diferente al de sus vecinos.
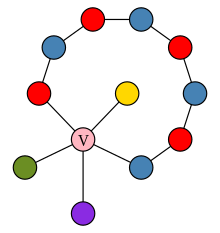
Kempe también demostró correctamente que G no puede tener vértices de grado 4. Como antes, eliminamos el vértice v y cuatricoloramos los vértices restantes. Si los cuatro vecinos de v son de diferentes colores, digamos rojo, verde, azul y amarillo en el sentido de las agujas del reloj, buscamos un camino alterno de vértices de color rojo y azul que unan a los vecinos rojo y azul. Este camino se llama cadena de Kempe . Puede haber una cadena de Kempe que une a los vecinos rojo y azul, y puede haber una cadena de Kempe que une a los vecinos verde y amarillo, pero no ambas, ya que estos dos caminos necesariamente se cruzarían, y el vértice donde se cruzan no se puede colorear. Supongamos que son los vecinos rojo y azul los que no están encadenados. Explore todos los vértices unidos al vecino rojo mediante caminos alternos rojo-azul y luego invierta los colores rojo y azul en todos estos vértices. El resultado sigue siendo un color de cuatro colores válido, y ahora se puede volver a agregar v y colorearlo de rojo.
Esto deja sólo el caso en el que G tiene un vértice de grado 5; pero el argumento de Kempe era erróneo en este caso. Heawood notó el error de Kempe y también observó que si uno estuviera satisfecho con demostrar que sólo se necesitan cinco colores, podría repasar el argumento anterior (cambiando sólo que el contraejemplo mínimo requiere 6 colores) y usar cadenas de Kempe en la situación de grado 5 para probar el Teorema de los cinco colores .
En cualquier caso, para abordar este caso de vértice de grado 5 se requiere una noción más complicada que eliminar un vértice. Más bien, la forma del argumento se generaliza a la consideración de configuraciones , que son subgrafos conectados de G con el grado de cada vértice (en G) especificado. Por ejemplo, el caso descrito en la situación de vértice de grado 4 es la configuración que consta de un único vértice etiquetado como de grado 4 en G. Como se indicó anteriormente, es suficiente demostrar que si se elimina la configuración y el gráfico restante tiene cuatro colores, entonces el color se puede modificar de tal manera que cuando se vuelve a agregar la configuración, los cuatro colores se pueden extender a él como Bueno. Una configuración para la cual esto es posible se llama configuración reducible . Si al menos una de un conjunto de configuraciones debe ocurrir en algún lugar de G, ese conjunto se llama inevitable . El argumento anterior comenzó dando un conjunto inevitable de cinco configuraciones (un solo vértice con grado 1, un solo vértice con grado 2,..., un solo vértice con grado 5) y luego procedió a mostrar que los primeros 4 son reducibles; exhibir un conjunto inevitable de configuraciones donde cada configuración del conjunto es reducible probaría el teorema.
Debido a que G es triangular, se conoce el grado de cada vértice en una configuración y se conocen todos los bordes internos de la configuración, el número de vértices en G adyacentes a una configuración dada es fijo y se unen en un ciclo. Estos vértices forman el anillo de la configuración; una configuración con k vértices en su anillo es una configuración de k -anillo, y la configuración junto con su anillo se llama configuración anillada . Como en los casos simples anteriores, se pueden enumerar todos los cuatro colores distintos del anillo; cualquier coloración que pueda extenderse sin modificación a una coloración de la configuración se llama inicialmente buena . Por ejemplo, la configuración de un solo vértice anterior con 3 o menos vecinos fue inicialmente buena. En general, el gráfico circundante debe cambiarse de color sistemáticamente para que el color del anillo sea bueno, como se hizo en el caso anterior donde había 4 vecinos; para una configuración general con un anillo más grande, esto requiere técnicas más complejas. Debido a la gran cantidad de cuatro colores distintos del anillo, este es el paso principal que requiere asistencia informática.
Finalmente, queda por identificar un conjunto inevitable de configuraciones susceptibles de reducción mediante este procedimiento. El método principal utilizado para descubrir dicho conjunto es el método de descarga . La idea intuitiva que subyace a la descarga es considerar el gráfico plano como una red eléctrica. Inicialmente, la "carga eléctrica" positiva y negativa se distribuye entre los vértices de modo que el total sea positivo.
Recuerde la fórmula anterior:
A cada vértice se le asigna una carga inicial de 6 grados ( v ). Luego se "fluye" la carga redistribuyéndola sistemáticamente desde un vértice a sus vértices vecinos de acuerdo con un conjunto de reglas, el procedimiento de descarga . Como la carga se conserva, algunos vértices todavía tienen carga positiva. Las reglas restringen las posibilidades de configuraciones de vértices cargados positivamente, por lo que enumerar todas esas configuraciones posibles da un conjunto inevitable.
Mientras algún miembro del conjunto inevitable no sea reducible, se modifica el procedimiento de descarga para eliminarlo (al tiempo que se introducen otras configuraciones). El procedimiento de alta final de Appel y Haken fue extremadamente complejo y, junto con una descripción del conjunto de configuraciones inevitables resultante, llenó un volumen de 400 páginas, pero las configuraciones que generó se pudieron verificar mecánicamente para que fueran reducibles. La verificación del volumen que describe el conjunto de configuración inevitable se realizó mediante revisión por pares durante un período de varios años.
Un detalle técnico que no se analiza aquí pero que se requiere para completar la prueba es la reducibilidad por inmersión .
El teorema de los cuatro colores ha sido conocido por atraer una gran cantidad de demostraciones y refutaciones falsas a lo largo de su larga historia. Al principio, The New York Times se negó, por cuestión de política, a informar sobre la prueba de Appel-Haken, temiendo que se demostrara que era falsa como las anteriores. [8] [ página necesaria ] Algunas supuestas pruebas, como las de Kempe y Tait mencionadas anteriormente, estuvieron bajo escrutinio público durante más de una década antes de ser refutadas. Pero muchos más, escritos por aficionados, nunca se publicaron.
Generalmente, los contraejemplos más simples, aunque inválidos, intentan crear una región que toque todas las demás regiones. Esto obliga a colorear las regiones restantes con sólo tres colores. Como el teorema de los cuatro colores es verdadero, esto siempre es posible; sin embargo, debido a que la persona que dibuja el mapa se concentra en una región grande, no se da cuenta de que las regiones restantes, de hecho, se pueden colorear con tres colores.
Este truco se puede generalizar: hay muchos mapas en los que si se seleccionan de antemano los colores de algunas regiones, resulta imposible colorear las regiones restantes sin exceder los cuatro colores. Un verificador casual del contraejemplo puede no pensar en cambiar los colores de estas regiones, de modo que el contraejemplo parezca válido.
Quizás un efecto subyacente a esta idea errónea común es el hecho de que la restricción de color no es transitiva : una región sólo tiene que tener un color diferente de las regiones que toca directamente, no de las regiones que tocan las regiones que toca. Si esta fuera la restricción, los gráficos planos requerirían una cantidad arbitrariamente grande de colores.
Otras refutaciones falsas violan los supuestos del teorema, como usar una región que consta de múltiples partes desconectadas o no permitir que regiones del mismo color se toquen en un punto.

Si bien cada mapa plano se puede colorear con cuatro colores, es NP-completo en complejidad decidir si un mapa plano arbitrario se puede colorear con solo tres colores. [22]
Un mapa cúbico se puede colorear con sólo tres colores si y sólo si cada región interior tiene un número par de regiones vecinas. [23] En el ejemplo del mapa de los estados de EE. UU., Missouri ( MO ) sin salida al mar tiene ocho vecinos (un número par): debe tener un color diferente al de todos ellos, pero los vecinos pueden alternar colores, por lo que esta parte del mapa solo necesita tres colores. Sin embargo, Nevada ( NV ) sin salida al mar tiene cinco vecinos (un número impar): uno de los vecinos debe tener un color diferente al de él y de todos los demás, por lo que aquí se necesitan cuatro colores.
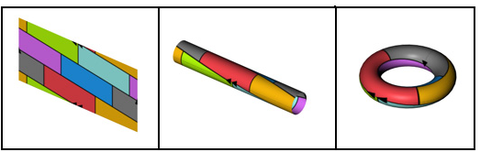
El teorema de los cuatro colores se aplica no sólo a gráficos planos finitos, sino también a gráficos infinitos que se pueden dibujar sin cruces en el plano, y aún más en general a gráficos infinitos (posiblemente con un número incontable de vértices) para los cuales cada subgrafo finito es plano. . Para probar esto, se puede combinar una prueba del teorema para gráficos planos finitos con el teorema de De Bruijn-Erdős que establece que, si cada subgrafo finito de un gráfico infinito es k -coloreable, entonces todo el gráfico también es k -coloreable Nash- Williams (1967). Esto también puede verse como una consecuencia inmediata del teorema de compacidad de Kurt Gödel para la lógica de primer orden , simplemente expresando la colorabilidad de un gráfico infinito con un conjunto de fórmulas lógicas.
También se puede considerar el problema de la coloración en superficies distintas al plano. [24] El problema sobre la esfera o el cilindro es equivalente al del plano. Para superficies cerradas (orientables o no orientables) con género positivo , el número máximo p de colores necesarios depende de la característica de Euler de la superficie χ según la fórmula
donde los corchetes más externos indican la función del piso .
Alternativamente, para una superficie orientable , la fórmula se puede dar en términos del género de una superficie, g :
Esta fórmula, la conjetura de Heawood , fue propuesta por PJ Heawood en 1890 y, después de las contribuciones de varias personas, probada por Gerhard Ringel y JWT Youngs en 1968. La única excepción a la fórmula es la botella de Klein , que tiene la característica de Euler 0 (de ahí la fórmula da p = 7) pero requiere sólo 6 colores, como lo demostró Philip Franklin en 1934.
Por ejemplo, el toroide tiene la característica de Euler χ = 0 (y género g = 1) y por tanto p = 7, por lo que no se requieren más de 7 colores para colorear cualquier mapa en un toroide. Este límite superior de 7 es nítido : ciertos poliedros toroidales como el poliedro Szilassi requieren siete colores.
Una tira de Möbius requiere seis colores (Tietze 1910), al igual que los gráficos uniplanares (gráficos dibujados con como máximo un cruce simple por borde) (Borodin 1984). Si tanto los vértices como las caras de un gráfico plano están coloreados, de tal manera que no hay dos vértices, caras o pares vértice-cara adyacentes que tengan el mismo color, entonces nuevamente se necesitan como máximo seis colores (Borodin 1984).
Para gráficos cuyos vértices se representan como pares de puntos en dos superficies distintas, con bordes dibujados como curvas que no se cruzan en una de las dos superficies, el número cromático puede ser al menos 9 y como máximo 12, pero no se necesitan límites más precisos. conocido; Este es el problema Tierra-Luna de Gerhard Ringel . [25]
No existe una extensión obvia del resultado de la coloración a regiones sólidas tridimensionales. Usando un conjunto de n varillas flexibles, se puede hacer que cada varilla toque a las demás. El conjunto requeriría entonces n colores, o n +1, incluido el espacio vacío que también toca cada varilla. El número n puede considerarse cualquier número entero, tan grande como se desee. Fredrick Guthrie conocía estos ejemplos en 1880. [8] [ página necesaria ] Incluso para cuboides paralelos a sus ejes (considerados adyacentes cuando dos cuboides comparten un área límite bidimensional) puede ser necesario un número ilimitado de colores (Reed & Allwright 2008; Magnant y Martín (2011)).
Dror Bar-Natan dio una declaración sobre las álgebras de Lie y las invariantes de Vassiliev que equivale al teorema de los cuatro colores. [26]
A pesar de la motivación de colorear mapas políticos de países , el teorema no es de particular interés para los cartógrafos . Según un artículo del historiador de matemáticas Kenneth May , "Los mapas que utilizan sólo cuatro colores son raros, y los que lo hacen normalmente requieren sólo tres. Los libros sobre cartografía e historia de la cartografía no mencionan la propiedad de los cuatro colores". [27] El teorema tampoco garantiza el requisito cartográfico habitual de que las regiones no contiguas del mismo país (como el enclave de Alaska y el resto de los Estados Unidos ) tengan colores idénticos.