En geometría , un sistema de coordenadas cartesiano ( Reino Unido : / k ɑːr ˈ t iː zj ə n / , EE. UU .: / k ɑːr ˈ t iː ʒ ə n / ) en un plano es un sistema de coordenadas que especifica cada punto de forma única mediante un par de Números reales llamados coordenadas , que son las distancias con signo al punto desde dos líneas orientadas perpendiculares fijas , llamadas líneas de coordenadas , ejes de coordenadas o simplemente ejes (plural de eje ) del sistema. El punto donde se encuentran se llama origen y tiene como coordenadas (0, 0) .
De manera similar, la posición de cualquier punto en el espacio tridimensional se puede especificar mediante tres coordenadas cartesianas , que son las distancias con signo desde el punto a tres planos mutuamente perpendiculares. De manera más general, n coordenadas cartesianas especifican el punto en un espacio euclidiano de n dimensiones para cualquier dimensión n . Estas coordenadas son las distancias con signo desde el punto hasta n hiperplanos fijos mutuamente perpendiculares .
Las coordenadas cartesianas llevan el nombre de René Descartes , cuya invención en el siglo XVII revolucionó las matemáticas al permitir la expresión de problemas de geometría en términos de álgebra y cálculo . Usando el sistema de coordenadas cartesiano, las formas geométricas (como las curvas ) se pueden describir mediante ecuaciones que involucran las coordenadas de los puntos de la forma. Por ejemplo, un círculo de radio 2, centrado en el origen del plano, puede describirse como el conjunto de todos los puntos cuyas coordenadas xey satisfacen la ecuación x 2 + y 2 = 4 ; El área , el perímetro y la recta tangente en cualquier punto se pueden calcular a partir de esta ecuación usando integrales y derivadas , de una manera que se puede aplicar a cualquier curva.
Las coordenadas cartesianas son la base de la geometría analítica y proporcionan interpretaciones geométricas esclarecedoras para muchas otras ramas de las matemáticas, como el álgebra lineal , el análisis complejo , la geometría diferencial , el cálculo multivariado , la teoría de grupos y más. Un ejemplo familiar es el concepto de gráfica de una función . Las coordenadas cartesianas también son herramientas esenciales para la mayoría de las disciplinas aplicadas que se ocupan de la geometría, incluidas la astronomía , la física , la ingeniería y muchas más. Son el sistema de coordenadas más común utilizado en gráficos por computadora , diseño geométrico asistido por computadora y otros procesamientos de datos relacionados con la geometría .
El adjetivo cartesiano hace referencia al matemático y filósofo francés René Descartes , quien publicó esta idea en 1637 mientras residía en Países Bajos . Fue descubierto de forma independiente por Pierre de Fermat , quien también trabajó en tres dimensiones, aunque Fermat no publicó el descubrimiento. [1] La clérigo francesa Nicole Oresme utilizó construcciones similares a las coordenadas cartesianas mucho antes de la época de Descartes y Fermat. [2]
Tanto Descartes como Fermat utilizaron un único eje en sus tratamientos y tienen una longitud variable medida en referencia a este eje. [ cita necesaria ] El concepto de utilizar un par de ejes se introdujo más tarde, después de que Frans van Schooten y sus estudiantes tradujeran La Géométrie de Descartes al latín en 1649 . Estos comentaristas introdujeron varios conceptos al intentar aclarar las ideas contenidas en la obra de Descartes. [3]
El desarrollo del sistema de coordenadas cartesiano jugaría un papel fundamental en el desarrollo del cálculo por parte de Isaac Newton y Gottfried Wilhelm Leibniz . [4] La descripción de dos coordenadas del plano se generalizó posteriormente al concepto de espacios vectoriales . [5]
Desde Descartes se han desarrollado muchos otros sistemas de coordenadas, como las coordenadas polares del plano y las coordenadas esféricas y cilíndricas del espacio tridimensional.
Una recta afín con un sistema de coordenadas cartesiano elegido se llama recta numérica . Cada punto de la recta tiene una coordenada de número real y cada número real representa algún punto de la recta.
Hay dos grados de libertad en la elección del sistema de coordenadas cartesianas para una línea, que se pueden especificar eligiendo dos puntos distintos a lo largo de la línea y asignándolos a dos números reales distintos (más comúnmente cero y uno). Luego se pueden asignar otros puntos de forma única a números mediante interpolación lineal . De manera equivalente, se puede asignar un punto a un número real específico, por ejemplo, un punto de origen correspondiente a cero, y se puede elegir como unidad una longitud orientada a lo largo de la línea, indicando la orientación la correspondencia entre las direcciones a lo largo de la línea y las direcciones positivas o positivas. números negativos. [6] Cada punto corresponde a su distancia con signo desde el origen (un número con un valor absoluto igual a la distancia y un signo + o − elegido según la dirección).
Una transformación geométrica de la línea se puede representar mediante una función de una variable real , por ejemplo la traslación de la línea corresponde a la suma y el escalado de la línea corresponde a la multiplicación. Dos sistemas de coordenadas cartesianas cualesquiera en la línea se pueden relacionar entre sí mediante una función lineal (función de la forma ) que toma la coordenada de un punto específico en un sistema con sus coordenadas en el otro sistema. La elección de un sistema de coordenadas para cada una de dos líneas diferentes establece un mapa afín de una línea a la otra, llevando cada punto de una línea al punto de la otra línea con la misma coordenada.
Un sistema de coordenadas cartesiano en dos dimensiones (también llamado sistema de coordenadas rectangular o sistema de coordenadas ortogonales [7] ) está definido por un par ordenado de líneas perpendiculares (ejes), una única unidad de longitud para ambos ejes y una orientación para cada uno. eje. El punto donde se encuentran los ejes se toma como origen para ambos, convirtiendo así cada eje en una recta numérica. Para cualquier punto P , se traza una línea que pasa por P perpendicular a cada eje, y la posición donde se encuentra con el eje se interpreta como un número. Los dos números, en ese orden elegido, son las coordenadas cartesianas de P. La construcción inversa permite determinar el punto P dadas sus coordenadas.
La primera y segunda coordenadas se denominan abscisa y ordenada de P , respectivamente; y el punto donde se encuentran los ejes se llama origen del sistema de coordenadas. Las coordenadas generalmente se escriben como dos números entre paréntesis, en ese orden, separados por una coma, como en (3, −10,5) . Así, el origen tiene coordenadas (0, 0) , y los puntos en los semiejes positivos, a una unidad del origen, tienen coordenadas (1, 0) y (0, 1) .
En matemáticas, física e ingeniería, el primer eje suele definirse o representarse como horizontal y orientado hacia la derecha, y el segundo eje es vertical y orientado hacia arriba. (Sin embargo, en algunos contextos de gráficos por computadora , el eje de ordenadas puede estar orientado hacia abajo). El origen suele estar etiquetado como O y las dos coordenadas suelen indicarse con las letras X e Y , o x e y . Los ejes pueden entonces denominarse eje X y eje Y. La elección de letras proviene de la convención original, que consiste en utilizar la última parte del alfabeto para indicar valores desconocidos. La primera parte del alfabeto se utilizó para designar valores conocidos.
Un plano euclidiano con un sistema de coordenadas cartesiano elegido se llamaPlano cartesiano . En un plano cartesiano, se pueden definir representantes canónicos de ciertas figuras geométricas, como elcírculo unitario(con radio igual a la unidad de longitud y centro en el origen), elcuadrado unitario(cuya diagonal tiene extremos en(0, 0)y(1, 1)), lahipérbola unitaria, y así sucesivamente.
Los dos ejes dividen el plano en cuatro ángulos rectos , llamados cuadrantes . Los cuadrantes pueden nombrarse o numerarse de varias maneras, pero el cuadrante donde todas las coordenadas son positivas generalmente se llama primer cuadrante .
Si las coordenadas de un punto son ( x , y ) , entonces sus distancias desde el eje X y desde el eje Y son | y | y | x |, respectivamente; donde | · | denota el valor absoluto de un número.
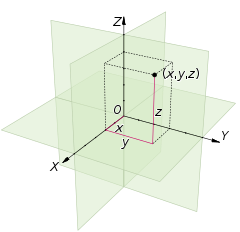
Un sistema de coordenadas cartesiano para un espacio tridimensional consta de un triplete ordenado de líneas (los ejes ) que pasan por un punto común (el origen ) y son perpendiculares por pares; una orientación para cada eje; y una única unidad de longitud para los tres ejes. Como en el caso bidimensional, cada eje se convierte en una recta numérica. Para cualquier punto P del espacio, se considera un hiperplano que pasa por P perpendicular a cada eje de coordenadas e interpreta el punto donde ese hiperplano corta el eje como un número. Las coordenadas cartesianas de P son esos tres números, en el orden elegido. La construcción inversa determina el punto P dadas sus tres coordenadas.
Alternativamente, cada coordenada de un punto P puede tomarse como la distancia de P al hiperplano definido por los otros dos ejes, con el signo determinado por la orientación del eje correspondiente.
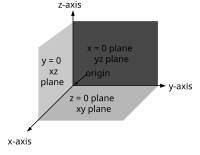
Cada par de ejes define un hiperplano de coordenadas . Estos hiperplanos dividen el espacio en ocho octantes . Los octantes son:
Las coordenadas generalmente se escriben como tres números (o fórmulas algebraicas) entre paréntesis y separados por comas, como en (3, −2,5, 1) o ( t , u + v , π /2) . Así, el origen tiene coordenadas (0, 0, 0) y los puntos unitarios en los tres ejes son (1, 0, 0) , (0, 1, 0) y (0, 0, 1) .
No existen nombres estándar para las coordenadas de los tres ejes (sin embargo, a veces se utilizan los términos abscisa , ordenada y aplicada ). Las coordenadas a menudo se indican con las letras X , Y y Z , o x , y y z . Los ejes pueden entonces denominarse eje X , eje Y y eje Z , respectivamente. Entonces, los hiperplanos de coordenadas pueden denominarse plano XY , plano YZ y plano XZ .
En contextos de matemáticas, física e ingeniería, los dos primeros ejes suelen definirse o representarse como horizontales, con el tercer eje apuntando hacia arriba. En ese caso la tercera coordenada puede llamarse altura o altitud . La orientación generalmente se elige de modo que el ángulo de 90 grados desde el primer eje hasta el segundo eje mire en el sentido contrario a las agujas del reloj cuando se ve desde el punto (0, 0, 1) ; una convención que comúnmente se llama regla de la mano derecha .
Dado que las coordenadas cartesianas son únicas y no ambiguas, los puntos de un plano cartesiano pueden identificarse con pares de números reales ; es decir, con el producto cartesiano , donde es el conjunto de todos los números reales. De la misma forma, los puntos de cualquier espacio euclidiano de dimensión n se identificarán con las tuplas (listas) de n números reales; es decir, con el producto cartesiano .
El concepto de coordenadas cartesianas se generaliza para permitir ejes que no son perpendiculares entre sí y/o diferentes unidades a lo largo de cada eje. En ese caso, cada coordenada se obtiene proyectando el punto sobre un eje en una dirección paralela al otro eje (o, en general, al hiperplano definido por todos los demás ejes). En un sistema de coordenadas tan oblicuo, los cálculos de distancias y ángulos deben modificarse con respecto a los sistemas cartesianos estándar, y muchas fórmulas estándar (como la fórmula pitagórica para la distancia) no se cumplen (ver plano afín ).
Las coordenadas cartesianas de un punto suelen escribirse entre paréntesis y separadas por comas, como en (10, 5) o (3, 5, 7) . El origen suele estar etiquetado con la letra O mayúscula . En geometría analítica, las coordenadas desconocidas o genéricas a menudo se indican con las letras ( x , y ) en el plano y ( x , y , z ) en el espacio tridimensional. Esta costumbre proviene de una convención de álgebra, que utiliza letras cerca del final del alfabeto para valores desconocidos (como las coordenadas de puntos en muchos problemas geométricos) y letras cerca del principio para cantidades dadas.
Estos nombres convencionales se utilizan a menudo en otros dominios, como la física y la ingeniería, aunque se pueden utilizar otras letras. Por ejemplo, en un gráfico que muestra cómo varía la presión con el tiempo , las coordenadas del gráfico se pueden indicar p y t . Cada eje suele recibir el nombre de la coordenada que se mide a lo largo de él; entonces se dice eje x , eje y , eje t , etc.
Otra convención común para la denominación de coordenadas es utilizar subíndices, como ( x 1 , x 2 , ..., x n ) para las n coordenadas en un espacio de n dimensiones, especialmente cuando n es mayor que 3 o no está especificado. Algunos autores prefieren la numeración ( x 0 , x 1 , ..., x n −1 ). Estas notaciones son especialmente ventajosas en programación informática : al almacenar las coordenadas de un punto como una matriz , en lugar de un registro , el subíndice puede servir para indexar las coordenadas.
En las ilustraciones matemáticas de sistemas cartesianos bidimensionales, la primera coordenada (tradicionalmente llamada abscisa ) se mide a lo largo de un eje horizontal , orientado de izquierda a derecha. Luego, la segunda coordenada (la ordenada ) se mide a lo largo de un eje vertical , generalmente orientado de abajo hacia arriba. Los niños pequeños que aprenden el sistema cartesiano, comúnmente aprenden el orden para leer los valores antes de consolidar los conceptos de los ejes x , y y z , comenzando con mnemónicos 2D (por ejemplo, 'Camina por el pasillo y luego sube las escaleras' similar en línea recta a lo largo del eje x y luego hacia arriba verticalmente a lo largo del eje y ).
Sin embargo, los gráficos por computadora y el procesamiento de imágenes a menudo utilizan un sistema de coordenadas con el eje y orientado hacia abajo en la pantalla de la computadora. Esta convención se desarrolló en la década de 1960 (o antes) a partir de la forma en que las imágenes se almacenaban originalmente en búferes de visualización .
Para sistemas tridimensionales, una convención es representar el plano xy horizontalmente, con el eje z agregado para representar la altura (positivo hacia arriba). Además, existe una convención para orientar el eje x hacia el espectador, sesgado hacia la derecha o hacia la izquierda. Si un diagrama ( proyección 3D o dibujo en perspectiva 2D ) muestra los ejes x e y horizontal y verticalmente, respectivamente, entonces el eje z debe mostrarse apuntando "fuera de la página" hacia el espectador o la cámara. En un diagrama 2D de este tipo de un sistema de coordenadas 3D, el eje z aparecería como una línea o rayo que apunta hacia abajo y hacia la izquierda o hacia abajo y hacia la derecha, dependiendo de la supuesta perspectiva del espectador o de la cámara . En cualquier diagrama o visualización, la orientación de los tres ejes, en su conjunto, es arbitraria. Sin embargo, la orientación de los ejes entre sí siempre debe cumplir con la regla de la mano derecha , a menos que se indique específicamente lo contrario. Todas las leyes de la física y las matemáticas asumen esta diestra, lo que garantiza la coherencia.
Para diagramas 3D, los nombres "abscisa" y "ordenada" rara vez se utilizan para x e y , respectivamente. Cuando lo son, la coordenada z a veces se denomina aplicación . Las palabras abscisa , ordenada y aplicación se utilizan a veces para referirse a ejes de coordenadas en lugar de valores de coordenadas. [7]
Los ejes de un sistema cartesiano bidimensional dividen el plano en cuatro regiones infinitas, llamadas cuadrantes , [7] cada una limitada por dos semiejes. A menudo se numeran del 1 al 4 y se indican con números romanos : I (donde ambas coordenadas tienen signos positivos), II (donde la abscisa es negativa - y la ordenada es positiva +), III (donde tanto la abscisa como la ordenada son −), y IV (abscisa +, ordenada −). Cuando los ejes se dibujan según la costumbre matemática, la numeración va en sentido antihorario comenzando desde el cuadrante superior derecho ("noreste").
De manera similar, un sistema cartesiano tridimensional define una división del espacio en ocho regiones u octantes , [7] según los signos de las coordenadas de los puntos. La convención utilizada para nombrar un octante específico es enumerar sus signos; por ejemplo, (+ + +) o (− + −) . La generalización del cuadrante y el octante a un número arbitrario de dimensiones es el ortante , y se aplica un sistema de denominación similar.
La distancia euclidiana entre dos puntos del plano con coordenadas cartesianas y es
Esta es la versión cartesiana del teorema de Pitágoras . En el espacio tridimensional, la distancia entre puntos y es
que puede obtenerse mediante dos aplicaciones consecutivas del teorema de Pitágoras. [8]
Las transformaciones euclidianas o movimientos euclidianos son asignaciones ( biyectivas ) de puntos del plano euclidiano entre sí que preservan las distancias entre puntos. Hay cuatro tipos de estos mapeos (también llamados isometrías): traslaciones , rotaciones , reflexiones y reflexiones de deslizamiento . [9]
Traducir un conjunto de puntos del plano, preservando las distancias y direcciones entre ellos, equivale a sumar un par fijo de números ( a , b ) a las coordenadas cartesianas de cada punto del conjunto. Es decir, si las coordenadas originales de un punto son ( x , y ) , después de la traslación serán
Rotar una figura en sentido antihorario alrededor del origen en algún ángulo equivale a reemplazar cada punto con coordenadas ( x , y ) por el punto con coordenadas ( x ' , y' ), donde
De este modo:
Si ( x , y ) son las coordenadas cartesianas de un punto, entonces (− x , y ) son las coordenadas de su reflexión a través del segundo eje de coordenadas (el eje y), como si esa línea fuera un espejo. Asimismo, ( x , − y ) son las coordenadas de su reflexión a través del primer eje de coordenadas (el eje x). En términos más generales, la reflexión a través de una línea que pasa por el origen formando un ángulo con el eje x, equivale a reemplazar cada punto con coordenadas ( x , y ) por el punto con coordenadas ( x ′, y ′ ) , donde
De este modo:
Una reflexión deslizante es la composición de una reflexión a través de una línea seguida de una traslación en la dirección de esa línea. Se puede observar que el orden de estas operaciones no importa (la traducción puede ir primero, seguida de la reflexión).
Todas las transformaciones afines del plano se pueden describir de forma uniforme mediante el uso de matrices. Para este propósito, las coordenadas de un punto se representan comúnmente como la matriz de columnas. El resultado de aplicar una transformación afín a un punto viene dado por la fórmula
Entre las transformaciones afines, las transformaciones euclidianas se caracterizan porque la matriz es ortogonal ; es decir, sus columnas son vectores ortogonales de la norma euclidiana uno, o, explícitamente,
Esto equivale a decir que A multiplicado por su transpuesta es la matriz identidad . Si estas condiciones no se cumplen, la fórmula describe una transformación afín más general .
La transformación es una traslación si y sólo si A es la matriz identidad . La transformación es una rotación alrededor de algún punto si y sólo si A es una matriz de rotación , lo que significa que es ortogonal y
Una reflexión o reflexión de deslizamiento se obtiene cuando,
Suponiendo que no se utilizan traducciones (es decir, ), las transformaciones se pueden componer simplemente multiplicando las matrices de transformación asociadas. En el caso general, es útil utilizar la matriz aumentada de la transformación; es decir, reescribir la fórmula de transformación
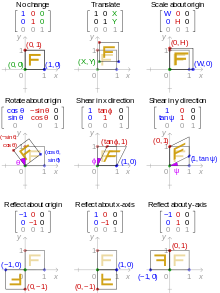
Las transformaciones afines del plano euclidiano son transformaciones que asignan líneas a líneas, pero pueden cambiar distancias y ángulos. Como se dijo en el apartado anterior, se pueden representar con matrices aumentadas:
Las transformaciones euclidianas son transformaciones afines tales que la matriz 2 × 2 de es ortogonal .
La matriz aumentada que representa la composición de dos transformaciones afines se obtiene multiplicando sus matrices aumentadas.
Algunas transformaciones afines que no son transformaciones euclidianas han recibido nombres específicos.
Un ejemplo de una transformación afín que no es euclidiana se da mediante el escalado. Hacer más grande o más pequeña una figura equivale a multiplicar las coordenadas cartesianas de cada punto por el mismo número positivo m . Si ( x , y ) son las coordenadas de un punto en la figura original, el punto correspondiente en la figura escalada tiene coordenadas
Si m es mayor que 1, la cifra se hace más grande; si m está entre 0 y 1, se vuelve más pequeño.
Una transformación de corte empujará la parte superior de un cuadrado hacia los lados para formar un paralelogramo. El corte horizontal se define por:
El corte también se puede aplicar verticalmente:
Fijar o elegir el eje x determina la dirección del eje y . Es decir, el eje y es necesariamente la perpendicular al eje x que pasa por el punto marcado 0 en el eje x . Pero existe la posibilidad de elegir cuál de las dos semilíneas de la perpendicular designar como positiva y cuál como negativa. Cada una de estas dos opciones determina una orientación diferente (también llamada lateralidad ) del plano cartesiano.
La forma habitual de orientar el plano, con el eje x positivo apuntando hacia la derecha y el eje y positivo apuntando hacia arriba (y siendo el eje x el "primero" y el eje y el "segundo"), se considera la Orientación positiva o estándar , también llamada orientación diestra .
Una mnemónica comúnmente utilizada para definir la orientación positiva es la regla de la mano derecha . Colocando una mano derecha algo cerrada en el plano con el pulgar apuntando hacia arriba, los dedos apuntan desde el eje x al eje y , en un sistema de coordenadas orientado positivamente.
La otra forma de orientar el avión es siguiendo la regla de la mano izquierda , colocando la mano izquierda sobre el avión con el pulgar apuntando hacia arriba.
Cuando apunta el pulgar lejos del origen a lo largo de un eje hacia positivo, la curvatura de los dedos indica una rotación positiva a lo largo de ese eje.
Independientemente de la regla utilizada para orientar el plano, rotar el sistema de coordenadas preservará la orientación. Cambiar cualquier eje invertirá la orientación, pero cambiar ambos dejará la orientación sin cambios.
Una vez que se especifican los ejes x e y , determinan la línea a lo largo de la cual debe estar el eje z , pero hay dos orientaciones posibles para esta línea. Los dos posibles sistemas de coordenadas resultantes se denominan "diestros" y "zurdos". [11] La orientación estándar, donde el plano xy es horizontal y el eje z apunta hacia arriba (y los ejes x e y forman un sistema de coordenadas bidimensional orientado positivamente en el plano xy si se observa desde arriba del plano xy ) se llama diestro o positivo .
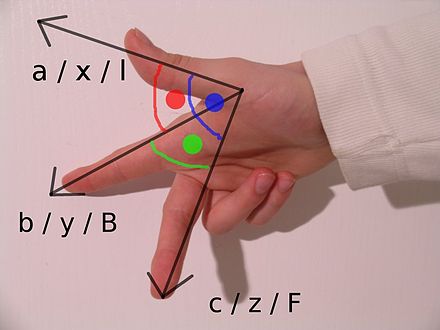
El nombre deriva de la regla de la mano derecha . Si el dedo índice de la mano derecha apunta hacia adelante, el dedo medio doblado hacia adentro en ángulo recto con respecto a él y el pulgar colocado en ángulo recto con ambos, los tres dedos indican la orientación relativa de x -, y -, y ejes z en un sistema diestro . El pulgar indica el eje x , el dedo índice el eje y y el dedo medio el eje z . Por el contrario, si se hace lo mismo con la mano izquierda, se obtiene un sistema para zurdos.
La Figura 7 muestra un sistema de coordenadas izquierdo y derecho. Debido a que un objeto tridimensional se representa en la pantalla bidimensional, se produce distorsión y ambigüedad. El eje que apunta hacia abajo (y hacia la derecha) también apunta hacia el observador, mientras que el eje "medio" apunta en dirección contraria al observador. El círculo rojo es paralelo al plano horizontal xy e indica la rotación desde el eje x al eje y (en ambos casos). Por tanto, la flecha roja pasa por delante del eje z .
La Figura 8 es otro intento de representar un sistema de coordenadas diestro. Nuevamente, existe una ambigüedad causada por la proyección del sistema de coordenadas tridimensional en el plano. Muchos observadores ven la Figura 8 como un "volteo hacia adentro y hacia afuera" entre un cubo convexo y una "esquina" cóncava. Esto corresponde a las dos posibles orientaciones del espacio. Ver la figura como convexa da un sistema de coordenadas para zurdos. Por tanto, la forma "correcta" de ver la Figura 8 es imaginar que el eje x apunta hacia el observador y, por tanto, ve una esquina cóncava.
Un punto en el espacio en un sistema de coordenadas cartesiano también puede representarse mediante un vector de posición , que puede considerarse como una flecha que apunta desde el origen del sistema de coordenadas hasta el punto. [12] Si las coordenadas representan posiciones espaciales (desplazamientos), es común representar el vector desde el origen hasta el punto de interés como . En dos dimensiones, el vector desde el origen hasta el punto con coordenadas cartesianas (x, y) se puede escribir como:
donde y son vectores unitarios en la dirección del eje x y del eje y respectivamente, generalmente denominados base estándar (en algunas áreas de aplicación también pueden denominarse versores ). De manera similar, en tres dimensiones, el vector desde el origen hasta el punto con coordenadas cartesianas se puede escribir como: [13]
dónde y
No existe una interpretación natural de multiplicar vectores para obtener otro vector que funcione en todas las dimensiones; sin embargo, existe una manera de utilizar números complejos para proporcionar dicha multiplicación. En un plano cartesiano bidimensional, identifica el punto de coordenadas ( x , y ) con el número complejo z = x + iy . Aquí, i es la unidad imaginaria y se identifica con el punto de coordenadas (0, 1) , por lo que no es el vector unitario en la dirección del eje x . Dado que los números complejos se pueden multiplicar dando otro número complejo, esta identificación proporciona un medio para "multiplicar" vectores. En un espacio cartesiano tridimensional se puede hacer una identificación similar con un subconjunto de los cuaterniones .
