Funcion exponencial

Función matemática, denotada exp(x) o e^x

Funciones exponenciales con bases 2 y 1/2

La función exponencial es una función matemática denotada por o (donde el argumento x se escribe como exponente ). A menos que se especifique lo contrario, el término generalmente se refiere a la función de valor positivo de una variable real , aunque puede extenderse a los números complejos o generalizarse a otros objetos matemáticos como matrices o álgebras de Lie . La función exponencial se originó a partir de la operación de tomar potencias de un número (multiplicación repetida), pero diversas definiciones modernas permiten extenderla rigurosamente a todos los argumentos reales , incluidos los números irracionales . Su omnipresente aparición en las matemáticas puras y aplicadas llevó al matemático Walter Rudin a considerar la función exponencial como "la función más importante en matemáticas". ^[1] ${\displaystyle f(x)=\exp(x)}$ ${\displaystyle e^{x}}$ ${\displaystyle x}$

Las funciones para números reales positivos también se conocen como funciones exponenciales y satisfacen la identidad de exponenciación : ${\displaystyle f(x)=b^{x}}$ ${\displaystyle b}$

$${\displaystyle b^{x+y}=b^{x}b^{y}{\text{ for all }}x,y\in \mathbb {R} .}$$

constante matemáticanúmero de Eulerfunción exponencialfunción exponencial natural01 ${\displaystyle b^{n}=b\times \cdots \times b}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle b=b^{1}}$ ${\displaystyle e=\exp(1)=2.71828\ldots }$ ${\displaystyle \exp(x)=e^{x}}$

${\displaystyle \exp '(x)=\exp(x)}$para todos , y ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle \exp(0)=1.}$

La relación para y real o compleja permite expresar funciones exponenciales generales en términos de la exponencial natural. ${\displaystyle b^{x}=e^{x\ln b}}$ ${\displaystyle b>0}$ ${\displaystyle x}$

De manera más general, especialmente en entornos aplicados, cualquier función definida por ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$

$${\displaystyle f(x)=ce^{ax}=cb^{kx},{\text{ with }}k=a/\ln b,\ a\neq 0,\ b,c>0}$$

También se conoce como función exponencial, ya que resuelve el problema del valor inicial , lo que significa que su tasa de cambio en cada punto es proporcional al valor de la función en ese punto. Este comportamiento modela diversos fenómenos en las ciencias biológicas, físicas y sociales, por ejemplo, el crecimiento sin restricciones de una población que se reproduce a sí misma , la desintegración de un elemento radiactivo , el interés compuesto que se acumula en un fondo financiero o un creciente cuerpo de experiencia en fabricación. . ${\displaystyle f'=af,\ f(0)=c}$

La función exponencial real también se puede definir como una serie de potencias , que se extiende fácilmente a argumentos complejos para definir la función exponencial compleja . Esta función toma todos los valores complejos excepto 0 y está estrechamente relacionada con las funciones trigonométricas complejas , como lo muestra la fórmula de Euler : ${\displaystyle \exp :\mathbb {C} \to \mathbb {C} }$

${\displaystyle e^{x+iy}=e^{x}\cos(y)\,+\,i\,e^{x}\sin(y).}$

Motivada por sus propiedades y caracterizaciones más abstractas, la función exponencial se puede generalizar a contextos mucho más amplios, como matrices cuadradas y grupos de Lie . Aún más, la definición de ecuación diferencial se puede generalizar a una variedad de Riemann .

La función exponencial real es una biyección del intervalo . ^[2] Su función inversa es el logaritmo natural , denotado , ^{[nb 1]} , ^{[nb 2]} o , y algunos textos antiguos ^[3] lo denominaron antilogaritmo . ${\displaystyle \mathbb {R} }$ ${\displaystyle (0,\infty )}$ ${\displaystyle \ln }$ ${\displaystyle \log }$ ${\displaystyle \log _{e}}$

Grafico

La gráfica de tiene pendiente ascendente y aumenta más rápido a medida que aumenta x . ^[4] La gráfica siempre se encuentra por encima del eje x , pero se acerca arbitrariamente a él para x negativos grandes ; por tanto, el eje x es una asíntota horizontal . La ecuación significa que la pendiente de la tangente a la gráfica en cada punto es igual a su coordenada y en ese punto. ${\displaystyle y=e^{x}}$ ${\displaystyle {\tfrac {d}{dx}}e^{x}=e^{x}}$

Relación con funciones exponenciales más generales

La función exponencial a veces se denomina función exponencial natural para distinguirla de las otras funciones exponenciales. El estudio de cualquier función exponencial se puede reducir fácilmente al de la función exponencial natural, ya que, por definición, para b positivo , ${\displaystyle f(x)=e^{x}}$

$${\displaystyle b^{x}\mathrel {\stackrel {\text{def}}{=}} e^{x\ln b}}$$

Como funciones de una variable real, las funciones exponenciales se caracterizan únicamente por el hecho de que la derivada de dicha función es directamente proporcional al valor de la función. La constante de proporcionalidad de esta relación es el logaritmo natural de base b :

$${\displaystyle {\frac {d}{dx}}b^{x}={\frac {d}{dx}}e^{x\ln(b)}=e^{x\ln(b)}\ln(b)=b^{x}\ln(b).}$$

Para b > 1 , la función es creciente (como se muestra para b = e y b = 2 ), porque hace que la derivada siempre sea positiva; A esto se le suele denominar crecimiento exponencial . Para b < 1 positivo , la función es decreciente (como se muestra para b = ${\displaystyle b^{x}}$ ${\displaystyle \ln b>0}$1/2); esto a menudo se conoce como decaimiento exponencial . Para b = 1 , la función es constante.

El número de Euler e = 2,71828... ^[5] es la única base para la cual la constante de proporcionalidad es 1, ya que , de modo que la función es su propia derivada: ${\displaystyle \ln(e)=1}$

$${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}\ln(e)=e^{x}.}$$

Esta función, también denominada exp x , se denomina "función exponencial natural", ^{[6] [7]} o simplemente "la función exponencial". Dado que cualquier función exponencial definida por puede escribirse en términos de la exponencial natural como , es computacional y conceptualmente conveniente reducir el estudio de funciones exponenciales a esta en particular. Por tanto, la exponencial natural se denota por ${\displaystyle f(x)=b^{x}}$ ${\displaystyle b^{x}=e^{x\ln b}}$

$${\displaystyle x\mapsto e^{x}}$$

$${\displaystyle x\mapsto \exp x.}$$

La primera notación se usa comúnmente para exponentes más simples, mientras que la segunda se prefiere cuando el exponente es más complicado y difícil de leer en una fuente pequeña.

Para números reales c y d , una función de la forma también es una función exponencial, ya que se puede reescribir como ${\displaystyle f(x)=ab^{cx+d}}$

$${\displaystyle ab^{cx+d}=\left(ab^{d}\right)\left(b^{c}\right)^{x}.}$$

Definicion formal

La función exponencial (en azul) y la suma de los primeros n + 1 términos de su serie de potencias (en rojo).

La función exponencial real se puede caracterizar de diversas formas equivalentes. Se define comúnmente mediante la siguiente serie de potencias : ^{[1] [8]} ${\displaystyle \exp :\mathbb {R} \to \mathbb {R} }$

$${\displaystyle \exp x:=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+{\frac {x^{4}}{24}}+\cdots }$$

Dado que el radio de convergencia de esta serie de potencias es infinito, esta definición es, de hecho, aplicable a todos los números complejos; ver § Plano complejo para la extensión al plano complejo. Usando la serie de potencias, la constante e se puede definir como ${\displaystyle \exp x}$ ${\textstyle e=\exp 1=\sum _{k=0}^{\infty }(1/k!)\,.}$

La diferenciación término por término de esta serie de potencias revela que para todo x real , lo que lleva a otra caracterización común de como solución única de la ecuación diferencial ${\textstyle {\frac {d}{dx}}\exp x=\exp x}$ ${\displaystyle \exp x}$

$${\displaystyle y'(x)=y(x)}$$

${\displaystyle y(0)=1.}$

Con base en esta caracterización, la regla de la cadena muestra que su función inversa, el logaritmo natural , satisface para o Esta relación conduce a una definición menos común de la función exponencial real como la solución de la ecuación ${\textstyle {\frac {d}{dy}}\ln y=1/y}$ ${\displaystyle y>0,}$ ${\textstyle \ln y=\int _{1}^{y}{\frac {dt}{t}}\,.}$ ${\displaystyle \exp(x)}$ ${\displaystyle y}$

$${\displaystyle x=\int _{1}^{y}{\frac {1}{t}}\,dt.}$$

Al resolver la ecuación diferencial ordinaria con la condición inicial utilizando el método de Euler se obtiene la fórmula límite del producto, válida para todos los valores complejos de : ^{[9] [8]} ${\displaystyle y'(x)=y(x)}$ ${\displaystyle y'(0)=1}$ ${\displaystyle x}$

$${\displaystyle \exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.}$$

Se puede demostrar que toda solución continua , distinta de cero, de la ecuación funcional para es una función exponencial, con ${\displaystyle f(x+y)=f(x)f(y)}$ ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ ${\displaystyle f(x)=e^{kx}}$ ${\displaystyle k\in \mathbb {R} .}$

Descripción general

La curva roja es la función exponencial. Las líneas horizontales negras muestran dónde cruza las líneas verticales verdes.

La función exponencial surge siempre que una cantidad crece o decrece a un ritmo proporcional a su valor actual. Una de esas situaciones es el interés compuesto continuo y, de hecho, fue esta observación la que llevó a Jacob Bernoulli en 1683 ^[10] a la cifra

$${\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}$$

eJohann Bernoulli^[10]

Si un monto principal de 1 genera intereses a una tasa anual de x compuesta mensualmente, entonces el interés ganado cada mes esX/12veces el valor actual, por lo que cada mes el valor total se multiplica por (1 +X/12) , y el valor al final del año es (1 +X/12) ¹² . Si en cambio el interés se capitaliza diariamente, éste se convierte en (1 +X/365) ³⁶⁵ . Dejar que el número de intervalos de tiempo por año crezca sin límite conduce a la definición límite de la función exponencial,

$${\displaystyle \exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}$$

Leonhard Euler^[9]caracterizaciones de la función exponencialseriesecuaciones diferenciales

A partir de cualquiera de estas definiciones se puede demostrar que e ^{− x} es el recíproco de e ^x . Por ejemplo, de la definición de ecuación diferencial, e ^x e ^{− x} = 1 cuando x = 0 y su derivada usando la regla del producto es e ^x e ^{− x} − e ^x e ^{− x} = 0 para todo x , entonces e ^x e ^{− x} = 1 para todo x .

A partir de cualquiera de estas definiciones se puede demostrar que la función exponencial obedece a la identidad de exponenciación básica . Por ejemplo, de la definición de serie de potencias,

$${\displaystyle \exp(x+y)=\sum _{m=0}^{\infty }{\frac {(x+y)^{m}}{m!}}=\sum _{m=0}^{\infty }\sum _{k=0}^{m}{\frac {m!}{k!(m-k)!}}{\frac {x^{k}y^{m-k}}{m!}}=\sum _{n=0}^{\infty }\sum _{k=0}^{\infty }{\frac {x^{k}y^{n}}{k!n!}}=\exp x\cdot \exp y\,.}$$

e ^xexp x

La derivada (tasa de cambio) de la función exponencial es la función exponencial misma. De manera más general, una función con una tasa de cambio proporcional a la función misma (en lugar de igual a ella) se puede expresar en términos de la función exponencial. Esta propiedad de la función conduce a un crecimiento exponencial o a una caída exponencial .

La función exponencial se extiende a una función completa en el plano complejo . La fórmula de Euler relaciona sus valores en argumentos puramente imaginarios con funciones trigonométricas . La función exponencial también tiene análogos cuyo argumento es una matriz , o incluso un elemento de un álgebra de Banach o de un álgebra de Lie .

Derivadas y ecuaciones diferenciales

La derivada de la función exponencial es igual al valor de la función. Desde cualquier punto P de la curva (azul), dibuje una línea tangente (roja) y una línea vertical (verde) con altura h , formando un triángulo rectángulo con una base b en el eje x . Dado que la pendiente de la recta tangente roja (la derivada) en P es igual a la relación entre la altura del triángulo y la base del triángulo (elevación sobre el recorrido), y la derivada es igual al valor de la función, h debe ser igual a la relación de h a b . Por tanto, la base b siempre debe ser 1.

La importancia de la función exponencial en matemáticas y ciencias proviene principalmente de su propiedad como función única que es igual a su derivada y es igual a 1 cuando x = 0 . Eso es,

$${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}\quad {\text{and}}\quad e^{0}=1.}$$

Las funciones de la forma ce ^x para c constante son las únicas funciones que son iguales a su derivada (según el teorema de Picard-Lindelöf ). Otras formas de decir lo mismo incluyen:

• La pendiente de la gráfica en cualquier punto es la altura de la función en ese punto.
• La tasa de aumento de la función en x es igual al valor de la función en x .
• La función resuelve la ecuación diferencial y ′ = y .
• exp es un punto fijo de derivada como funcional .

Si la tasa de crecimiento o decaimiento de una variable es proporcional a su tamaño, como es el caso del crecimiento poblacional ilimitado (ver catástrofe maltusiana ), el interés compuesto continuo o la desintegración radiactiva , entonces la variable se puede escribir como una constante multiplicada por una función exponencial del tiempo. . Explícitamente para cualquier constante real k , una función f : R → R satisface f ′ = kf si y sólo si f ( x ) = ce ^kx para alguna constante c . La constante k se llama constante de desintegración , constante de desintegración , ^[11] constante de velocidad , ^[12] o constante de transformación . ^[13]

Además, para cualquier función diferenciable f , encontramos, por la regla de la cadena :

$${\displaystyle {\frac {d}{dx}}e^{f(x)}=f'(x)e^{f(x)}.}$$

Fracciones continuas para e x

Se puede obtener una fracción continua para e ^x mediante una identidad de Euler :

$${\displaystyle e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-\ddots }}}}}}}}}$$

La siguiente fracción continua generalizada para e ^z converge más rápidamente: ^[14]

$${\displaystyle e^{z}=1+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{10+{\cfrac {z^{2}}{14+\ddots }}}}}}}}}$$

o, aplicando la sustitución z =X/y:

$${\displaystyle e^{\frac {x}{y}}=1+{\cfrac {2x}{2y-x+{\cfrac {x^{2}}{6y+{\cfrac {x^{2}}{10y+{\cfrac {x^{2}}{14y+\ddots }}}}}}}}}$$

z = 2

$${\displaystyle e^{2}=1+{\cfrac {4}{0+{\cfrac {2^{2}}{6+{\cfrac {2^{2}}{10+{\cfrac {2^{2}}{14+\ddots \,}}}}}}}}=7+{\cfrac {2}{5+{\cfrac {1}{7+{\cfrac {1}{9+{\cfrac {1}{11+\ddots \,}}}}}}}}}$$

Esta fórmula también converge, aunque más lentamente, para z > 2 . Por ejemplo:

$${\displaystyle e^{3}=1+{\cfrac {6}{-1+{\cfrac {3^{2}}{6+{\cfrac {3^{2}}{10+{\cfrac {3^{2}}{14+\ddots \,}}}}}}}}=13+{\cfrac {54}{7+{\cfrac {9}{14+{\cfrac {9}{18+{\cfrac {9}{22+\ddots \,}}}}}}}}}$$

Plano complejo

La función exponencial e^z trazada en el plano complejo desde -2-2i hasta 2+2i

Una trama compleja de , con el argumento representado por distintos tonos. La transición de colores oscuros a claros muestra que aumenta sólo hacia la derecha. Las bandas horizontales periódicas correspondientes a una misma tonalidad indican que es periódica en la parte imaginaria de . ${\displaystyle z\mapsto \exp z}$ ${\displaystyle \operatorname {Arg} \exp z}$ ${\displaystyle \left|\exp z\right|}$ ${\displaystyle z\mapsto \exp z}$ ${\displaystyle z}$

Como en el caso real , la función exponencial se puede definir en el plano complejo de varias formas equivalentes.

La definición más común de función exponencial compleja es paralela a la definición de serie de potencias para argumentos reales, donde la variable real se reemplaza por una compleja:

$${\displaystyle \exp z:=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}}$$

Alternativamente, la función exponencial compleja se puede definir modelando la definición del límite para argumentos reales, pero con la variable real reemplazada por una compleja:

$${\displaystyle \exp z:=\lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}}$$

Para la definición de la serie de potencias, la multiplicación por términos de dos copias de esta serie de potencias en el sentido de Cauchy , permitida por el teorema de Mertens , muestra que la propiedad multiplicativa definitoria de las funciones exponenciales continúa siendo válida para todos los argumentos complejos:

$${\displaystyle \exp(w+z)=\exp w\exp z{\text{ for all }}w,z\in \mathbb {C} }$$

La definición de la función exponencial compleja conduce a su vez a definiciones apropiadas que extienden las funciones trigonométricas a argumentos complejos.

En particular, cuando z = it ( t real), la definición de la serie produce la expansión

$${\displaystyle \exp(it)=\left(1-{\frac {t^{2}}{2!}}+{\frac {t^{4}}{4!}}-{\frac {t^{6}}{6!}}+\cdots \right)+i\left(t-{\frac {t^{3}}{3!}}+{\frac {t^{5}}{5!}}-{\frac {t^{7}}{7!}}+\cdots \right).}$$

En esta expansión, la reordenación de los términos en partes reales e imaginarias se justifica por la convergencia absoluta de la serie. Las partes real e imaginaria de la expresión anterior corresponden de hecho a las expansiones en serie de cos t y sin t , respectivamente.

Esta correspondencia proporciona motivación para definir el coseno y el seno de todos los argumentos complejos en términos de y la serie de potencias equivalente: ^[15] ${\displaystyle \exp(\pm iz)}$

$${\displaystyle {\begin{aligned}&\cos z:={\frac {\exp(iz)+\exp(-iz)}{2}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k}}{(2k)!}},\\[5pt]{\text{and }}\quad &\sin z:={\frac {\exp(iz)-\exp(-iz)}{2i}}=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k+1}}{(2k+1)!}}\end{aligned}}}$$

para todos ${\textstyle z\in \mathbb {C} .}$

Las funciones exp , cos y sin así definidas tienen radios de convergencia infinitos según la prueba de la razón y, por lo tanto, son funciones enteras (es decir, holomorfas en ). El rango de la función exponencial es , mientras que los rangos de las funciones complejas seno y coseno son ambos en su totalidad, de acuerdo con el teorema de Picard , que afirma que el rango de una función entera no constante es todo o excluye un valor lacunar . ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} \setminus \{0\}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$ ${\displaystyle \mathbb {C} }$

Estas definiciones de las funciones exponencial y trigonométrica conducen trivialmente a la fórmula de Euler :

$${\displaystyle \exp(iz)=\cos z+i\sin z{\text{ for all }}z\in \mathbb {C} .}$$

Alternativamente, podríamos definir la función exponencial compleja basándose en esta relación. Si z = x + iy , donde x e y son reales, entonces podríamos definir su exponencial como

$${\displaystyle \exp z=\exp(x+iy):=(\exp x)(\cos y+i\sin y)}$$

expcossin^[dieciséis]

Para , la relación se cumple, de modo que para real y mapea la recta real (mod 2 π ) al círculo unitario en el plano complejo. Además, yendo de a , la curva definida por traza un segmento del círculo unitario de longitud ${\displaystyle t\in \mathbb {R} }$ ${\displaystyle {\overline {\exp(it)}}=\exp(-it)}$ ${\displaystyle \left|\exp(it)\right|=1}$ ${\displaystyle t}$ ${\displaystyle t\mapsto \exp(it)}$ ${\displaystyle t=0}$ ${\displaystyle t=t_{0}}$ ${\displaystyle \gamma (t)=\exp(it)}$

$${\displaystyle \int _{0}^{t_{0}}|\gamma '(t)|\,dt=\int _{0}^{t_{0}}|i\exp(it)|\,dt=t_{0},}$$

z = 1

La función exponencial compleja es periódica con período 2 πi y se cumple para todos . ${\displaystyle \exp(z+2\pi ik)=\exp z}$ ${\displaystyle z\in \mathbb {C} ,k\in \mathbb {Z} }$

Cuando su dominio se extiende desde la recta real al plano complejo, la función exponencial conserva las siguientes propiedades:

$${\displaystyle {\begin{aligned}&e^{z+w}=e^{z}e^{w}\,\\[5pt]&e^{0}=1\,\\[5pt]&e^{z}\neq 0\\[5pt]&{\frac {d}{dz}}e^{z}=e^{z}\\[5pt]&\left(e^{z}\right)^{n}=e^{nz},n\in \mathbb {Z} \end{aligned}}}$$

para todos ${\textstyle w,z\in \mathbb {C} .}$

Extendiendo el logaritmo natural a argumentos complejos se obtiene el logaritmo complejo log z , que es una función multivaluada .

Entonces podemos definir una exponenciación más general:

$${\displaystyle z^{w}=e^{w\log z}}$$

zwzlog zz ^wz

( e ^z )^w
≠ e ^zw , sino más bien ( e ^z )^w
= e ^{( z + 2 niπ ) w} multivalorado sobre números enteros n

Consulte falla de potencia e identidades de logaritmos para obtener más información sobre los problemas con la combinación de potencias.

La función exponencial asigna cualquier línea en el plano complejo a una espiral logarítmica en el plano complejo con el centro en el origen . Existen dos casos especiales: cuando la línea original es paralela al eje real, la espiral resultante nunca se cierra sobre sí misma; cuando la línea original es paralela al eje imaginario, la espiral resultante es un círculo de cierto radio.

• Gráficos 3D de parte real, parte imaginaria y módulo de la función exponencial
• 
  z = Re( e ^{x + iy} )
• 
  z = Im( e ^{x + iy} )
• 
  z = | e ^{x + iy} |

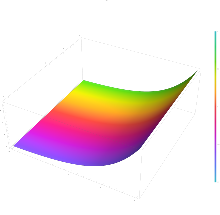
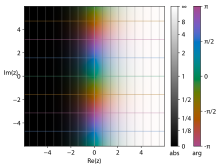
Considerando la función exponencial compleja como una función que involucra cuatro variables reales:

$${\displaystyle v+iw=\exp(x+iy)}$$

Comenzando con una parte del dominio codificada por colores, las siguientes son representaciones del gráfico proyectado de diversas formas en dos o tres dimensiones. ${\displaystyle xy}$

• Gráficas de la función exponencial compleja.
• 
  Clave del tablero de ajedrez:
  ${\displaystyle x>0:\;{\text{green}}}$
  ${\displaystyle x<0:\;{\text{red}}}$
  ${\displaystyle y>0:\;{\text{yellow}}}$
  ${\displaystyle y<0:\;{\text{blue}}}$
• 
  Proyección en el plano complejo de rango (V/W). Compare con la siguiente imagen en perspectiva.
• 
  Proyección en las dimensiones , , y , produciendo una forma de embudo o cuerno ensanchado (imaginado como una imagen en perspectiva 2D). ${\displaystyle x}$ ${\displaystyle v}$ ${\displaystyle w}$
• 
  Proyección en las dimensiones , , y , produciendo una forma de espiral. ( rango ampliado a ±2 π , nuevamente como imagen en perspectiva 2D). ${\displaystyle y}$ ${\displaystyle v}$ ${\displaystyle w}$ ${\displaystyle y}$

La segunda imagen muestra cómo el plano complejo de dominio se asigna al plano complejo de rango:

• cero se asigna a 1
• el eje real se asigna al eje real positivo ${\displaystyle x}$ ${\displaystyle v}$
• El eje imaginario gira alrededor del círculo unitario con una velocidad angular constante. ${\displaystyle y}$
• los valores con partes reales negativas se asignan dentro del círculo unitario
• los valores con partes reales positivas se asignan fuera del círculo unitario
• los valores con una parte real constante se asignan a círculos centrados en cero
• los valores con una parte imaginaria constante se asignan a rayos que se extienden desde cero

La tercera y cuarta imágenes muestran cómo el gráfico de la segunda imagen se extiende a una de las otras dos dimensiones que no se muestran en la segunda imagen.

La tercera imagen muestra el gráfico extendido a lo largo del eje real. Muestra que la gráfica es una superficie de revolución alrededor del eje de la gráfica de la función exponencial real, produciendo una forma de cuerno o embudo. ${\displaystyle x}$ ${\displaystyle x}$

La cuarta imagen muestra el gráfico extendido a lo largo del eje imaginario. Muestra que la superficie del gráfico para valores positivos y negativos en realidad no se encuentra a lo largo del eje real negativo, sino que forma una superficie en espiral alrededor del eje. Debido a que sus valores se han ampliado a ±2 π , esta imagen también representa mejor la periodicidad 2π en el valor imaginario. ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle v}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle y}$

Cálculo de a b donde tanto a como b son complejos

La exponenciación compleja a ^b se puede definir convirtiendo a a coordenadas polares y usando la identidad ( e ^{ln a} )^b
= a ^b :

$${\displaystyle a^{b}=\left(re^{\theta i}\right)^{b}=\left(e^{(\ln r)+\theta i}\right)^{b}=e^{\left((\ln r)+\theta i\right)b}}$$

Sin embargo, cuando b no es un número entero, esta función es multivaluada , porque θ no es única (ver Exponenciación § Fallo de identidades de potencia y logaritmos ).

Matrices y álgebras de Banach

La definición de serie de potencias de la función exponencial tiene sentido para matrices cuadradas (para las cuales la función se llama matriz exponencial ) y, más generalmente, en cualquier álgebra B de Banach unital . En esta configuración, e ⁰ = 1 , y e ^x es invertible con e inversa e ^{− x} para cualquier x en B. Si xy = yx , entonces e ^{x + y} = e ^x e ^y , pero esta identidad puede fallar para x e y que no conmutan .

Algunas definiciones alternativas conducen a la misma función. Por ejemplo, e ^x se puede definir como

$${\displaystyle \lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.}$$

O e ^x se puede definir como f _x (1) , donde f _x  : R → B es la solución de la ecuación diferencialdfx _{_}/dt( t ) = x  f _x ( t ) , con condición inicial f _x (0) = 1 ; se deduce que f _x ( t ) = e ^tx para cada t en R .

Álgebras de mentira

Dado un grupo de Lie G y su álgebra de Lie asociada , el mapa exponencial es un mapa ↦ G que satisface propiedades similares. De hecho, dado que R es el álgebra de Lie del grupo de Lie de todos los números reales positivos bajo multiplicación, la función exponencial ordinaria para argumentos reales es un caso especial de la situación del álgebra de Lie. De manera similar, dado que el grupo de Lie GL( n , R ) de matrices invertibles n × n tiene como álgebra de Lie M( n , R ) , el espacio de todas las matrices n × n , la función exponencial para matrices cuadradas es un caso especial de la Mapa exponencial de álgebra de mentira. ${\displaystyle {\mathfrak {g}}}$ ${\displaystyle {\mathfrak {g}}}$

La identidad puede fallar para los elementos xey del álgebra de Lie que no conmutan ; la fórmula de Baker-Campbell-Hausdorff proporciona los términos de corrección necesarios. ${\displaystyle \exp(x+y)=\exp(x)\exp(y)}$

Trascendencia

La función e ^z no está en el anillo de funciones racionales : no es el cociente de dos polinomios con coeficientes complejos. ${\displaystyle \mathbb {C} (z)}$

Si a ₁ , ..., a _n son números complejos distintos, entonces e ^{a ₁ z} , ..., e ^{a _n z} son linealmente independientes y, por tanto , e ^z es trascendental sobre . ${\displaystyle \mathbb {C} (z)}$ ${\displaystyle \mathbb {C} (z)}$

Cálculo

Al calcular (una aproximación de) la función exponencial cerca del argumento 0 , el resultado será cercano a 1, y calcular el valor de la diferencia con aritmética de punto flotante puede llevar a la pérdida de (posiblemente todas) las cifras significativas , produciendo una gran error de cálculo, posiblemente incluso un resultado sin sentido. ${\displaystyle e^{x}-1}$

Siguiendo una propuesta de William Kahan , puede ser útil tener una rutina dedicada, a menudo llamada expm1, para calcular e ^x − 1 directamente, sin pasar por el cálculo de e ^x . Por ejemplo, si la exponencial se calcula usando su serie de Taylor

$${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots +{\frac {x^{n}}{n!}}+\cdots ,}$$

${\displaystyle e^{x}-1}$

$${\displaystyle e^{x}-1=x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots +{\frac {x^{n}}{n!}}+\cdots .}$$

Esto se implementó por primera vez en 1979 en la calculadora Hewlett-Packard HP-41C y fue proporcionado por varias calculadoras, ^{[17] [18]} sistemas operativos (por ejemplo Berkeley UNIX 4.3BSD ^[19] ), sistemas de álgebra informática y lenguajes de programación ( por ejemplo C99 ). ^[20]

Además de la base e , el estándar IEEE 754-2008 define funciones exponenciales similares cerca de 0 para la base 2 y 10: y . ${\displaystyle 2^{x}-1}$ ${\displaystyle 10^{x}-1}$

Se ha utilizado un enfoque similar para el logaritmo (ver lnp1 ). ^{[nota 3]}

Una identidad en términos de la tangente hiperbólica ,

$${\displaystyle \operatorname {expm1} (x)=e^{x}-1={\frac {2\tanh(x/2)}{1-\tanh(x/2)}},}$$

xexpm1( x )

Ver también

• Portal de matemáticas

• Exponencial de Carlitz , un análogo característico de p
• Función exponencial doble  – Función exponencial de una función exponencial
• Campo exponencial  : campo matemático con una operación adicional.
• función gaussiana
• Función semiexponencial , raíz cuadrada composicional de una función exponencial
• Lambert_W_function#Solving_equations  – Función multivalor en matemáticas: se utiliza para resolver ecuaciones exponenciales
• Lista de temas exponenciales
• Lista de integrales de funciones exponenciales.
• Función Mittag-Leffler , una generalización de la función exponencial
• p -función exponencial ádica
• Tabla de Padé para función exponencial - Aproximación de Padé de función exponencial por una fracción de funciones polinómicas
• factor de fase

Notas

1. La notación ln x es el estándar ISO y prevalece en las ciencias naturales y la educación secundaria (EE. UU.). Sin embargo, algunos matemáticos (por ejemplo, Paul Halmos ) han criticado esta notación y prefieren utilizar log x para el logaritmo natural de x .
2. En matemáticas puras, la notación log x generalmente se refiere al logaritmo natural de x o a un logaritmo en general si la base es inmaterial.
3. Un enfoque similar para reducir los errores de redondeo de los cálculos para ciertos valores de entrada de funciones trigonométricas consiste en utilizar las funciones trigonométricas menos comunes versine , vercosine , coversine , covercosine , haversine , havercosine , hacoversine , hacovercosine , exsecante y excosecante .

Referencias

1. Rudin, Walter (1987). Análisis real y complejo (3ª ed.). Nueva York: McGraw-Hill . pag. 1.ISBN _ 978-0-07-054234-1.
2. Meier, Juan; Smith, Derek (7 de agosto de 2017). Explorando las Matemáticas . Prensa de la Universidad de Cambridge. pag. 167.ISBN _ 978-1-107-12898-9.
3. Conversar, Henry Augustus; Durell, Fletcher (1911). Trigonometría plana y esférica. Serie matemática de Durell. Compañía CE Merrill. pag. 12. Uso Inverso de una Tabla de Logaritmos; es decir, dado un logaritmo, encontrar el número que le corresponde, (llamado antilogaritmo)...[1]
4. "Referencia de función exponencial". www.mathsisfun.com . Consultado el 28 de agosto de 2020 .
5. Sloane, Nueva Jersey (ed.). "Secuencia A001113 (Expansión decimal de e)". La enciclopedia en línea de secuencias enteras . Fundación OEIS.
6. Goldstein, Larry Joel; Lay, David C.; Schneider, David I.; Asmar, Nakhle H. (2006). Cálculo breve y sus aplicaciones (11ª ed.). Prentice Hall. ISBN 978-0-13-191965-5.(467 páginas)
7. Corriente; Robbins (1996). Stewart (ed.). ¿Qué son las matemáticas? Un enfoque elemental de ideas y métodos (2ª edición revisada). Prensa de la Universidad de Oxford . pag. 448.ISBN _ 978-0-13-191965-5. Esta función exponencial natural es idéntica a su derivada. Esta es realmente la fuente de todas las propiedades de la función exponencial, y la razón básica de su importancia en las aplicaciones...
8. Weisstein, Eric W. "Función exponencial". mathworld.wolfram.com . Consultado el 28 de agosto de 2020 .
9. Maor, Eli . e: la historia de un número . pag. 156.
10. O'Connor, John J.; Robertson, Edmund F. (septiembre de 2001). "El número e". Escuela de Matemáticas y Estadística . Universidad de St Andrews, Escocia . Consultado el 13 de junio de 2011 .
11. Serway, Raymond A.; Moisés, Clemente J.; Moyer, Curt A. (1989). Física Moderna . "Fort Worth: Harcourt Brace Jovanovich" . pag. 384.ISBN _ 0-03-004844-3.
12. Simmons, George F. (1972). Ecuaciones diferenciales con aplicaciones y notas históricas . Nueva York: McGraw-Hill . pag. 15.LCCN 75173716  .
13. Enciclopedia McGraw-Hill de ciencia y tecnología (10ª ed.). Nueva York: McGraw-Hill . 2007.ISBN _ 978-0-07-144143-8.
14. Lorentzen, L .; Waadeland, H. (2008). "A.2.2 La función exponencial". Fracciones continuas . Estudios de la Atlántida en Matemáticas. vol. 1. pág. 268. doi :10.2991/978-94-91216-37-4. ISBN 978-94-91216-37-4.
15. Rudin, Walter (1976). Principios del análisis matemático. Nueva York: McGraw-Hill . pag. 182.ISBN _ 978-0-07-054235-8.
16. Apóstol, Tom M. (1974). Análisis matemático (2ª ed.). Lectura, Massachusetts: Addison Wesley . págs.19. ISBN 978-0-201-00288-1.
17. Serie HP 48G: manual de referencia del usuario avanzado (AUR) (4 ed.). Hewlett Packard . Diciembre de 1994 [1993]. HP 00048-90136, 0-88698-01574-2 . Consultado el 6 de septiembre de 2015 .
18. Manual de referencia del usuario avanzado (AUR) de la calculadora gráfica HP 50g / 49g+ / 48gII (2 ed.). Hewlett Packard . 2009-07-14 [2005]. HPF2228-90010 . Consultado el 10 de octubre de 2015 .[2]
19. Beebe, Nelson HF (22 de agosto de 2017). "Capítulo 10.2. Exponencial cercano a cero". Manual de computación de funciones matemáticas: programación utilizando la biblioteca de software portátil MathCW (1 ed.). Salt Lake City, UT, EE.UU.: Springer International Publishing AG . págs. 273–282. doi :10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN  2017947446. S2CID  30244721. Berkeley UNIX 4.3BSD introdujo la función expm1() en 1987.
20. Beebe, Nelson HF (9 de julio de 2002). "Cálculo de expm1 = exp(x)−1" (PDF) . 1.00. Salt Lake City, Utah, EE.UU.: Departamento de Matemáticas, Centro de Computación Científica, Universidad de Utah . Consultado el 2 de noviembre de 2015 .

enlaces externos

• "Función exponencial", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]