
En geometría , un lápiz es una familia de objetos geométricos con una propiedad común, por ejemplo, el conjunto de líneas que pasan por un punto dado en un plano , o el conjunto de círculos que pasan por dos puntos dados en un plano.
Aunque la definición de un lápiz es bastante vaga, la característica común es que el lápiz está completamente determinado por dos de sus miembros. Análogamente, un conjunto de objetos geométricos que están determinados por tres de sus miembros se llama haz . [ 1] Por lo tanto, el conjunto de todas las líneas que pasan por un punto en el espacio tridimensional es un haz de líneas, dos de las cuales determinan un lápiz de líneas. Para enfatizar la naturaleza bidimensional de un lápiz de este tipo, a veces se lo denomina lápiz plano . [2]
Cualquier objeto geométrico puede utilizarse en un lápiz. Los más comunes son líneas, planos, círculos, cónicas, esferas y curvas generales. Incluso se pueden utilizar puntos. Un lápiz de puntos es el conjunto de todos los puntos de una línea dada. [1] Un término más común para este conjunto es rango de puntos.
En un plano , sean u y v dos rectas distintas que se cortan. Para ser más concretos, supongamos que u tiene la ecuación aX + bY + c = 0 y que v tiene la ecuación a'X + b'Y + c′ = 0. Entonces
representa, para escalares adecuados λ y μ , cualquier línea que pase por la intersección de u = 0 y v = 0. Este conjunto de líneas que pasan por un punto común se llama lápiz de líneas . [3] El punto común de un lápiz de líneas se llama vértice del lápiz.
En un plano afín con la variante reflexiva del paralelismo , un conjunto de líneas paralelas forma una clase de equivalencia llamada lápiz de líneas paralelas . [4] Esta terminología es consistente con la definición anterior ya que en la extensión proyectiva única del plano afín a un plano proyectivo se agrega un solo punto ( punto en el infinito ) a cada línea en el lápiz de líneas paralelas, convirtiéndolo así en un lápiz en el sentido anterior en el plano proyectivo.
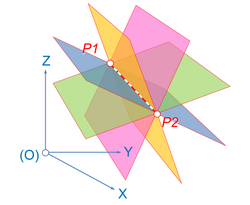
Un lápiz de planos es el conjunto de planos que pasan por una línea recta dada en el espacio tridimensional, llamado eje del lápiz. El lápiz a veces se denomina lápiz axial [5] o abanico de planos o haz de planos . [6] Por ejemplo, los meridianos del globo terráqueo están definidos por el lápiz de planos sobre el eje de rotación de la Tierra.
Dos planos que se intersectan se encuentran en una línea en el espacio tridimensional y, por lo tanto, determinan el eje y, por lo tanto, todos los planos del lápiz.
El cuatriespacio de cuaterniones puede verse como un lápiz axial de planos complejos que comparten todos la misma línea real. De hecho, los cuaterniones contienen una esfera de unidades imaginarias , y un par de puntos antípodas en esta esfera, junto con el eje real, generan un plano complejo. La unión de todos estos planos complejos constituye la 4-álgebra de cuaterniones.

Dos círculos cualesquiera en el plano tienen un eje radical común , que es la línea que consiste en todos los puntos que tienen la misma potencia con respecto a los dos círculos. Un lápiz de círculos (o sistema coaxial ) es el conjunto de todos los círculos en el plano con el mismo eje radical. [7] Para ser inclusivos, se dice que los círculos concéntricos tienen la línea en el infinito como eje radical.
Existen cinco tipos de círculos de lápiz, [8] las dos familias de círculos apolíneos de la ilustración anterior representan dos de ellos. Cada tipo está determinado por dos círculos llamados generadores del lápiz. Cuando se describen algebraicamente, es posible que las ecuaciones admitan soluciones imaginarias. Los tipos son:
Un círculo que es ortogonal a dos círculos fijos es ortogonal a cada círculo en el lápiz que ellos determinan. [11]
Los círculos ortogonales a dos círculos fijos forman un lápiz de círculos. [11]
Dos círculos determinan dos lápices, el único lápiz que los contiene y el lápiz de los círculos ortogonales a ellos. El eje radical de un lápiz está formado por los centros de los círculos del otro lápiz. Si un lápiz es de tipo elíptico, el otro es de tipo hiperbólico y viceversa. [11]
El eje radical de cualquier par de círculos, interpretado como un círculo de radio infinito, pertenece al lápiz. Tres círculos cualesquiera pertenecen a un lápiz común siempre que los tres pares compartan el mismo eje radical y sus centros sean colineales .
Existe una correspondencia natural entre círculos en el plano y puntos en el espacio proyectivo tridimensional ; una línea en este espacio corresponde a una familia continua unidimensional de círculos, por lo tanto, un lápiz de puntos en este espacio es un lápiz de círculos en el plano.
En concreto, la ecuación de un círculo de radio r centrado en un punto ( p , q ),
puede reescribirse como
donde α = 1, β = p , γ = q , y δ = p 2 + q 2 − r 2 . En esta forma, multiplicar el cuádruple ( α,β,γ,δ ) por un escalar produce un cuádruple diferente que representa el mismo círculo; por lo tanto, estos cuádruples pueden considerarse coordenadas homogéneas para el espacio de círculos. [12] Las líneas rectas también pueden representarse con una ecuación de este tipo en la que α = 0 y deben considerarse como una forma degenerada de un círculo. Cuando α ≠ 0 , podemos resolver para p = β/α, q = γ/α , y r =√( p 2 + q 2 − δ/α) ; La última fórmula puede dar r = 0 (en cuyo caso el círculo degenera en un punto) o r igual a un número imaginario (en cuyo caso se dice que el cuádruple ( α, β, γ, δ ) representa un círculo imaginario ).
El conjunto de combinaciones afines de dos círculos ( α 1 ,β 1 ,γ 1 ,δ 1 ), ( α 2 ,β 2 ,γ 2 ,δ 2 ), es decir, el conjunto de círculos representados por la cuádruple
para algún valor del parámetro z , forma un lápiz; los dos círculos son los generadores del lápiz.

Otro tipo de lápiz de círculos se puede obtener de la siguiente manera. Considérese un círculo dado (llamado círculo generador ) y un punto distinguido P en el círculo generador. El conjunto de todos los círculos que pasan por P y tienen sus centros en el círculo generador forman un lápiz de círculos. La envolvente de este lápiz es un cardioide .
Una esfera está determinada de forma única por cuatro puntos que no son coplanares . En términos más generales, una esfera está determinada de forma única por cuatro condiciones, como pasar por un punto, ser tangente a un plano, etc. [13] Esta propiedad es análoga a la propiedad de que tres puntos no coplanares determinan un círculo único en un plano.
En consecuencia, una esfera está determinada únicamente por (es decir, pasa a través de) un círculo y un punto que no está en el plano de ese círculo.
Al examinar las soluciones comunes de las ecuaciones de dos esferas , se puede ver que dos esferas se intersecan en un círculo y el plano que contiene ese círculo se llama plano radical de las esferas que se intersecan. [14] Aunque el plano radical es un plano real, el círculo puede ser imaginario (las esferas no tienen ningún punto real en común) o constar de un solo punto (las esferas son tangentes en ese punto). [15]
Si f ( x , y , z ) = 0 y g ( x , y , z ) = 0 son las ecuaciones de dos esferas distintas entonces
es también la ecuación de una esfera para valores arbitrarios de los parámetros λ y μ . El conjunto de todas las esferas que satisfacen esta ecuación se denomina lápiz de esferas determinado por las dos esferas originales. En esta definición, se permite que una esfera sea un plano (radio infinito, centro en el infinito) y si ambas esferas originales son planos, entonces todas las esferas del lápiz son planos; de lo contrario, solo hay un plano (el plano radical) en el lápiz. [16]
Si el lápiz de esferas no consta de todos los planos, entonces hay tres tipos de lápices: [15]
Todas las líneas tangentes desde un punto fijo del plano radical a las esferas de un lápiz tienen la misma longitud. [15]
El plano radical es el lugar geométrico de los centros de todas las esferas que son ortogonales a todas las esferas de un lápiz. Además, una esfera ortogonal a dos esferas cualesquiera de un lápiz de esferas es ortogonal a todas ellas y su centro se encuentra en el plano radical del lápiz. [15]
Una cónica (no degenerada) está completamente determinada por cinco puntos en posición general (no hay tres colineales) en un plano y el sistema de cónicas que pasa por un conjunto fijo de cuatro puntos (de nuevo en un plano y no hay tres colineales) se llama lápiz de cónicas . [17] Los cuatro puntos comunes se denominan puntos base del lápiz. Por cualquier punto que no sea un punto base, pasa una única cónica del lápiz. Este concepto generaliza un lápiz de círculos.
En un plano proyectivo definido sobre un cuerpo algebraicamente cerrado, dos cónicas cualesquiera se encuentran en cuatro puntos (contados con multiplicidad) y, por lo tanto, se determina el eje de cónicas en función de estos cuatro puntos. Además, los cuatro puntos base determinan tres pares de líneas ( cónicas degeneradas que pasan por los puntos base, cada línea del par contiene exactamente dos puntos base) y, por lo tanto, cada eje de cónicas contendrá como máximo tres cónicas degeneradas. [18]
Un lápiz de cónicas se puede representar algebraicamente de la siguiente manera. Sean C 1 y C 2 dos cónicas distintas en un plano proyectivo definido sobre un cuerpo algebraicamente cerrado K . Para cada par λ , μ de elementos de K , no ambos cero, la expresión:
representa una cónica en el lápiz determinada por C 1 y C 2 . Esta representación simbólica se puede concretar con un ligero abuso de notación (usando la misma notación para denotar el objeto así como la ecuación que define el objeto). Pensando en C 1 , digamos, como una forma cuadrática ternaria , entonces C 1 = 0 es la ecuación de la "cónica C 1 ". Otra realización concreta se obtendría al pensar en C 1 como la matriz simétrica 3×3 que la representa. Si C 1 y C 2 tienen tales realizaciones concretas, entonces cada miembro del lápiz anterior también las tendrá. Dado que la configuración utiliza coordenadas homogéneas en un plano proyectivo, dos representaciones concretas (ya sean ecuaciones o matrices) dan la misma cónica si difieren en una constante multiplicativa distinta de cero.
De manera más general, un lápiz es el caso especial de un sistema lineal de divisores en el que el espacio de parámetros es una línea proyectiva . Los lápices típicos de curvas en el plano proyectivo , por ejemplo, se escriben como
donde C = 0 , C ′ = 0 son curvas planas.
A Desargues se le atribuye la invención del término "lápiz de líneas" ( ordonnance de lignes ). [19]
Uno de los primeros autores de la geometría proyectiva moderna, GB Halsted, introdujo los términos copuntual y lápiz plano para definir el ángulo : "Las rectas con la misma cruz son copuntuales". También "El conjunto de todas las rectas copuntuales y coplanares se denomina lápiz plano " y "Un trozo de lápiz plano limitado por dos de las rectas como lados se denomina ángulo ". [20]