Juan Napier

Matemático escocés (1550-1617)

Estatua de John Napier, Galería Nacional de Retratos de Escocia

John Napier de Merchiston ( / ˈn eɪ p i ər / NAY -pee -ər ; ^[1] latinizado como Ioannes Neper ; 1 de febrero de 1550 - 4 de abril de 1617), apodado Marvellous Merchiston , fue un terrateniente escocés conocido como matemático , físico y astrónomo . Fue el octavo Laird de Merchiston .

John Napier es más conocido como el descubridor de los logaritmos . También inventó los llamados " huesos de Napier " y popularizó el uso del punto decimal en aritmética y matemáticas.

El lugar de nacimiento de Napier, la Torre Merchiston en Edimburgo , ahora forma parte de las instalaciones de la Universidad Napier de Edimburgo . Hay un monumento en su memoria en la iglesia de St Cuthbert, en el lado oeste de Edimburgo. ^[2]

Vida

El padre de Napier era Sir Archibald Napier del castillo de Merchiston, y su madre era Janet Bothwell, hija del político y juez Francis Bothwell , ^[3] y hermana de Adam Bothwell, que se convirtió en obispo de Orkney . Archibald Napier tenía 16 años cuando nació John Napier. ^[3]

Castillo de Merchiston en un grabado en madera de 1834

No hay registros de los primeros estudios de Napier, pero muchos creen que recibió clases particulares durante su infancia. A los 13 años, se matriculó en el St Salvator's College, St Andrews . Cerca del momento de su matriculación, la calidad de la educación proporcionada por la universidad era pobre, debido en parte a que la Reforma provocó conflictos entre los de la antigua fe y el creciente número de protestantes. No hay registros que muestren que John Napier completó su educación en St Andrews. ^[4] Se cree que dejó Escocia para continuar su educación en Europa continental, siguiendo el consejo dado por su tío Adam Bothwell en una carta escrita al padre de John Napier el 5 de diciembre de 1560, diciendo: "Le ruego, señor, que envíe a John a las escuelas ya sea en Francia o Flandes , porque no puede aprender nada bueno en casa". ^[5] No se sabe a qué universidad asistió Napier en Europa, pero cuando regresó a Escocia en 1571 hablaba griego con fluidez, un idioma que no se enseñaba comúnmente en las universidades europeas en ese momento. Tampoco hay registros que demuestren su inscripción en las principales universidades de París o Ginebra durante esta época. ^{[6] [4]}

En 1571, Napier, con 21 años, regresó a Escocia y compró un castillo en Gartness en 1574. A la muerte de su padre en 1608, Napier y su familia se mudaron al castillo de Merchiston en Edimburgo, donde residió el resto de su vida. También tenía una propiedad dentro de la ciudad de Edimburgo, en Borthwick's Close, junto a la Royal Mile . ^[7]

Monumento a John Napier en la iglesia de St Cuthbert, Edimburgo

El 7 de junio de 1596, Napier escribió un artículo titulado Invenciones secretas, útiles y necesarias en aquellos días para la defensa de esta isla . Describe dos tipos de espejos de combustión para usar contra barcos a distancia, un tipo especial de proyectil de artillería y un carro de metal a prueba de mosquetes. ^[8]

Napier murió a causa de los efectos de la gota en su casa del castillo de Merchiston a la edad de 67 años. Fue enterrado en el cementerio de St Giles en Edimburgo. Tras la pérdida del cementerio de St Giles para construir la Casa del Parlamento , sus restos fueron trasladados a una bóveda subterránea en el lado norte de la iglesia parroquial de St Cuthbert en el lado oeste de Edimburgo. ^[2] También hay un monumento mural a Napier en St Cuthbert. ^[2]

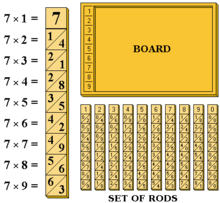
En aquella época, muchos matemáticos eran muy conscientes de los problemas de la computación y se dedicaban a aliviar a los profesionales de la carga de cálculo. Napier era famoso por sus dispositivos para ayudar con estos problemas de computación. Inventó un artefacto matemático muy conocido, las ingeniosas barras de numeración, más curiosamente conocidas como "huesos de Napier", ^[9] que ofrecían medios mecánicos para facilitar el cálculo.

Además, Napier reconoció el potencial de los recientes avances en matemáticas, en particular los de la prostaféresis , las fracciones decimales y la aritmética de índices simbólicos, para abordar la cuestión de la reducción de los cálculos. Comprendió que, en su mayor parte, los profesionales que tenían cálculos laboriosos generalmente los hacían en el contexto de la trigonometría. Por lo tanto, además de desarrollar la relación logarítmica, Napier la situó en un contexto trigonométrico para que fuera aún más relevante.

Matemáticas

Los huesos de Napier

Los huesos de Napier

Su obra Mirifici Logarithmorum Canonis Descriptio (1614) contenía cincuenta y siete páginas de material explicativo y noventa páginas de tablas que enumeraban los logaritmos naturales de las funciones trigonométricas . ^{[10] : Cap. III} El libro también tiene una discusión de teoremas en trigonometría esférica , usualmente conocidos como Reglas de partes circulares de Napier.

Se pueden encontrar en la web traducciones modernas al inglés de ambos libros de Napier sobre logaritmos y su descripción, así como un análisis de los huesos de Napier y del Promptuary (otro dispositivo de cálculo temprano). ^[11]

Su invención de los logaritmos fue rápidamente adoptada en el Gresham College , y el destacado matemático inglés Henry Briggs visitó a Napier en 1615. Entre los asuntos que discutieron se encontraba una nueva escala de los logaritmos de Napier, en la que la presencia de la constante matemática ahora conocida como e (más exactamente, e multiplicado por una gran potencia de 10 redondeada a un entero) era una dificultad práctica. Ni Napier ni Briggs descubrieron realmente la constante e ; ese descubrimiento lo hizo décadas después Jacob Bernoulli .

Napier delegó en Briggs el cálculo de una tabla revisada. El avance computacional disponible a través de los logaritmos, la inversa de los números potenciados o la notación exponencial , era tal que hacía que los cálculos a mano fueran mucho más rápidos. ^[12] Se abrió el camino a los avances científicos posteriores, en astronomía , dinámica y otras áreas de la física .

Napier realizó más contribuciones. Mejoró la notación decimal de Simon Stevin , introduciendo el punto (.) como delimitador de la parte fraccionaria. ^{[13] : p. 8, archivo p. 32)} La multiplicación reticular , utilizada por Fibonacci , se hizo más conveniente con la introducción de los huesos de Napier , una herramienta de multiplicación que utiliza un conjunto de varillas numeradas.

Napier puede haber trabajado en gran medida de forma aislada, pero tenía contacto con Tycho Brahe , quien se carteaba con su amigo John Craig . Craig ciertamente anunció el descubrimiento de los logaritmos a Brahe en la década de 1590 (el nombre en sí vino después); hay una historia de Anthony à Wood , tal vez no bien fundamentada, de que Napier recibió una pista de Craig de que Longomontanus , un seguidor de Brahe, estaba trabajando en una dirección similar. Craig tenía notas sobre un método de Paul Wittich que usaba identidades trigonométricas para reducir una fórmula de multiplicación para la función seno a sumas. ^[14]

Trigonometría

Cuando uno de los ángulos, digamos C , de un triángulo esférico es igual a π /2 las distintas identidades dadas anteriormente se simplifican considerablemente. Hay diez identidades que relacionan tres elementos elegidos del conjunto a , b , c , A , B.

Napier ^[15] proporcionó una elegante ayuda mnemotécnica para las diez ecuaciones independientes: la mnemotecnia se llama círculo de Napier o pentágono de Napier (cuando el círculo en la figura anterior, a la derecha, se reemplaza por un pentágono).

Primero, escribe las seis partes del triángulo (tres ángulos de vértice, tres ángulos de arco para los lados) en el orden en que ocurren alrededor de cualquier circuito del triángulo: para el triángulo que se muestra arriba a la izquierda, yendo en el sentido de las agujas del reloj comenzando con a da aCbAcB . Luego reemplaza las partes que no son adyacentes a C (es decir, A, c, B ) por sus complementos y luego elimina el ángulo C de la lista. Las partes restantes se pueden dibujar como cinco rebanadas iguales y ordenadas de un pentagrama o círculo, como se muestra en la figura anterior (derecha). Para cualquier elección de tres partes contiguas, una (la parte del medio ) será adyacente a dos partes y opuesta a las otras dos partes. Las diez reglas de Napier están dadas por

• seno de la parte media = producto de las tangentes de las partes adyacentes
• seno de la parte media = el producto de los cosenos de las partes opuestas

La clave para recordar qué función trigonométrica corresponde a cada parte es observar la primera vocal del tipo de parte: las partes del medio toman el seno, las partes adyacentes toman la tangente y las partes opuestas toman el coseno. Por ejemplo, comenzando con el sector que contiene tenemos: ${\displaystyle a}$

${\displaystyle \sin a=\tan(\pi /2-B)\,\tan b=\cos(\pi /2-c)\,\cos(\pi /2-A)=\cot B\,\tan b=\sin c\,\sin A.}$

El conjunto completo de reglas para el triángulo esférico rectángulo es (Todhunter, ^[16] Art.62)

${\displaystyle {\begin{alignedat}{4}&{\text{(R1)}}&\qquad \cos c&=\cos a\,\cos b,&\qquad \qquad &{\text{(R6)}}&\qquad \tan b&=\cos A\,\tan c,\\&{\text{(R2)}}&\sin a&=\sin A\,\sin c,&&{\text{(R7)}}&\tan a&=\cos B\,\tan c,\\&{\text{(R3)}}&\sin b&=\sin B\,\sin c,&&{\text{(R8)}}&\cos A&=\sin B\,\cos a,\\&{\text{(R4)}}&\tan a&=\tan A\,\sin b,&&{\text{(R9)}}&\cos B&=\sin A\,\cos b,\\&{\text{(R5)}}&\tan b&=\tan B\,\sin a,&&{\text{(R10)}}&\cos c&=\cot A\,\cot B.\end{alignedat}}}$

Un triángulo esférico cuadrantal junto con el círculo de Napier para utilizarlo en sus mnemotecnias

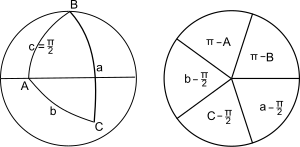
Un triángulo esférico cuadrantal se define como un triángulo esférico en el que uno de los lados subtiende un ángulo de π /2 radianes en el centro de la esfera: en la esfera unidad, el lado tiene una longitud de π /2. En el caso de que el lado c tenga una longitud de π /2 en la esfera unidad, las ecuaciones que rigen los lados y ángulos restantes se pueden obtener aplicando las reglas para el triángulo esférico rectángulo de la sección anterior al triángulo polar A'B'C' con lados a',b',c' tales que A' = π  −  a ,  a' =  π  −  A etc. Los resultados son:

${\displaystyle {\begin{alignedat}{4}&{\text{(Q1)}}&\qquad \cos C&=-\cos A\,\cos B,&\qquad \qquad &{\text{(Q6)}}&\qquad \tan B&=-\cos a\,\tan C,\\&{\text{(Q2)}}&\sin A&=\sin a\,\sin C,&&{\text{(Q7)}}&\tan A&=-\cos b\,\tan C,\\&{\text{(Q3)}}&\sin B&=\sin b\,\sin C,&&{\text{(Q8)}}&\cos a&=\sin b\,\cos A,\\&{\text{(Q4)}}&\tan A&=\tan a\,\sin B,&&{\text{(Q9)}}&\cos b&=\sin a\,\cos B,\\&{\text{(Q5)}}&\tan B&=\tan b\,\sin A,&&{\text{(Q10)}}&\cos C&=-\cot a\,\cot b.\end{alignedat}}}$

Logaritmo

Dado un número real positivo b tal que b ≠ 1, el logaritmo de un número real positivo x con respecto a la base b es el exponente por el cual b debe ser elevado para obtener x . En otras palabras, el logaritmo de x en base b es el único número real y tal que b ^y = x .

El logaritmo se denota "log _b  x " (pronunciado como "el logaritmo de x en base b ", "el logaritmo en base b de x " o, más comúnmente, "el logaritmo, base b , de x ").

Una definición equivalente y más sucinta es que la función es la función inversa de la función ${\displaystyle f\colon x\to log_{b}x}$ ${\displaystyle f\colon x\to b^{x}.}$

Teología

Portada de Mirifici logarithmorum canonis descriptio (1614)

Página de Mirifici logarithmorum canonis descriptio, para 45 grados

Napier se interesó por el Apocalipsis desde sus días de estudiante en el St. Salvator's College, St. Andrews . Bajo la influencia de los sermones de Christopher Goodman , desarrolló una lectura fuertemente antipapal, llegando tan lejos como para decir que el Papa era el Anticristo en algunos de sus escritos. ^{[12] [17]}

Napier consideró que A Plaine Discovery of the Whole Revelation of St. John (1593) era su obra más importante. Fue escrita en inglés, a diferencia de sus otras publicaciones, para llegar a la audiencia más amplia y para que, según Napier, "los simples de esta isla puedan ser instruidos". ^[17] A Plaine Discovery utilizó el análisis matemático del Libro del Apocalipsis para intentar predecir la fecha del Apocalipsis . Napier identificó eventos en orden cronológico que creía que eran paralelos a los eventos descritos en el Libro del Apocalipsis creyendo que la estructura del Apocalipsis implicaba que las profecías se cumplirían de manera incremental. ^[17] En esta obra, Napier fechó la séptima trompeta en 1541 y predijo que el fin del mundo ocurriría en 1688 o 1700. Napier no creía que la gente pudiera saber la verdadera fecha del Apocalipsis, pero afirmó que, dado que la Biblia contenía tantas pistas sobre el fin, Dios quería que la Iglesia supiera cuándo llegaría el fin. ^[17]

En su dedicatoria del Plaine Discovery a Jacobo VI , fechada el 29 de enero de 1594, ^[18] Napier instó al rey a que se ocupara de "que se hiciera justicia contra los enemigos de la iglesia de Dios", y aconsejó al rey "que reformara las enormidades universales de su país, y que primero comenzara por su propia casa, familia y corte". El volumen incluye nueve páginas de versos ingleses de Napier. Tuvo éxito en su país y en el extranjero. En 1600, Michiel Panneel produjo una traducción al holandés, que alcanzó una segunda edición en 1607. En 1602, la obra apareció en La Rochelle en una versión francesa, de Georges Thomson, revisada por Napier, y que también pasó por varias ediciones (1603, 1605 y 1607). En 1611 se solicitó una nueva edición del original en inglés, que fue revisada y corregida por el autor y ampliada con la adición de With a solving certain doubts, suggested by some well affect brethren [Con la resolución de ciertas dudas, propuesta por algunos hermanos bien afectados] ; ^[19] esta apareció simultáneamente en Edimburgo y Londres. El autor declaró que todavía tenía la intención de publicar una edición en latín, pero nunca apareció. Una traducción alemana, realizada por Leo de Dromna, de la primera parte de la obra de Napier apareció en Gera en 1611, y de la totalidad por Wolfgang Meyer en Frankfurt-am-Main , en 1615. ^[12] Entre los seguidores de Napier se encontraba Matthew Cotterius ( Matthieu Cottière ). ^[20]

Interés por lo oculto

Además de sus intereses matemáticos y religiosos, Napier era considerado a menudo un mago, y se cree que incursionó en la alquimia y la nigromancia . Se decía que viajaba con una araña negra en una pequeña caja, y que su gallo negro era su espíritu familiar . ^{[21] [22] [23]}

Algunos vecinos de Napier lo acusaron de ser un hechicero y estar en complicidad con el diablo, creyendo que todo el tiempo que pasaba en su estudio lo estaba utilizando para aprender el arte negro. Estos rumores se avivaron cuando Napier utilizó su gallo negro para atrapar a un ladrón. Napier les dijo a sus sirvientes que entraran en una habitación oscura y acariciaran al gallo, alegando que el pájaro cantaría si ellos eran los que robaban su propiedad. Sin que lo supieran los sirvientes, Napier había cubierto el pájaro con hollín y cuando los sirvientes salieron de la habitación, Napier inspeccionó sus manos para encontrar al que había tenido demasiado miedo de tocar el gallo. ^[24]

Otro acto que se dice que Napier llevó a cabo, y que puede haber parecido místico a los lugareños, fue cuando Napier sacó a las palomas de su propiedad porque estaban comiendo su grano. Napier atrapó a las palomas esparciendo grano mezclado con alcohol por todo el campo y luego capturó a las palomas una vez que estaban demasiado borrachas para volar. ^[25]

Todavía existe un contrato para una búsqueda del tesoro , realizado entre Napier y Robert Logan de Restalrig . Napier debía buscar en el castillo de Fast un tesoro supuestamente escondido allí, en el que se establece que Napier debería "hacer su máxima diligencia para buscar y descubrir, y por todos los medios para descubrirlo, o asegurarse de que tal cosa no ha estado allí". ^{[12] [26]} Este contrato nunca fue cumplido por Napier, y no se encontró oro cuando la Sociedad Arqueológica de Edimburgo excavó el castillo entre 1971 y 1986. ^[26]

Influencia

Entre los primeros seguidores de Napier se encontraban los fabricantes de instrumentos Edmund Gunter y John Speidell . ^{[27] [28] [29]} Se le atribuye al desarrollo de los logaritmos el mérito de ser el factor individual más importante en la adopción general de la aritmética decimal . ^[30] Las Trissotetras (1645) de Thomas Urquhart se basan en el trabajo de Napier en trigonometría . ^[31]

Henry Briggs fue uno de los primeros en adoptar el logaritmo neperiano. Más tarde calculó una nueva tabla de logaritmos de base 10, con una precisión de 14 decimales. ^[32]

Epónimos

Una unidad alternativa al decibelio utilizada en ingeniería eléctrica , el neper , recibe su nombre de Napier, al igual que la Universidad Napier de Edimburgo, en Edimburgo, Escocia.

El cráter Neper en la Luna lleva su nombre. ^[33]

En francés, español y portugués, el logaritmo natural lleva su nombre (respectivamente, Logarithme Népérien y Logaritmos Neperianos para español y portugués). En finés e italiano, la constante matemática e lleva su nombre ( Neperin luku y Numero di Nepero ).

Familia

En 1572, Napier se casó con Elizabeth, de 16 años, hija de James Stirling, cuarto Laird de Keir y de Cadder . ^[34] Tuvieron dos hijos. Elizabeth murió en 1579 y Napier se casó con Agnes Chisholm, con quien tuvo diez hijos más.

El suegro de Napier, Sir James Chisholm de Cromlix, fue uno de los muchos excomulgados por la Asamblea General del partido presbiteriano tras el complot de los blancos españoles . Napier formó parte de la Asamblea General que excomulgó a los conspiradores y solicitó al rey Jaime VI y a Jaime I que aplicaran el castigo a los conspiradores, pero finalmente fue ignorado ya que el rey creía que los ministros estaban actuando con crueldad y estaba a favor de seguir políticas de mayor apaciguamiento. ^{[17] [35]}

Su medio hermano (a través del nuevo matrimonio de su padre) fue Alexander Napier, Lord Laurieston .

Lista de obras

• (1593) Un descubrimiento claro de toda la revelación de San Juan
• (1614) Mirifici logarithmorum canonis descriptio Archivado el 27 de abril de 2023 en Wayback Machine – La traducción al inglés de Edward Wright se publicó en 1616. ^[10]
• (1617) Rabdologiæ seu Numerationis per Virgulas libri duo (enlace de Google Books) (publicado póstumamente) Rabdology (Wikipedia)
• (1619) Mirifici logarithmorum canonis constructio –escrito antes de la Descriptio , pero publicado póstumamente por su hijo Robert. Traducido al inglés en 1889. ^[36]
• (1839) De arte logístico

Véase también

• Lista de colegios y universidades que llevan el nombre de personas
• Aritmética de ubicación
• Las analogías de Napier
• Logaritmo neperiano
• Rabdología

Notas

1. "Napier" Archivado el 5 de marzo de 2016 en Wayback Machine . Random House Webster's Unabridged Dictionary .
2. Monumentos e inscripciones monumentales en Escocia: The Grampian Society, 1871
3. Chisholm, Hugh , ed. (1911). "Napier, John"  . Encyclopædia Britannica . Vol. 19 (11.ª ed.). Cambridge University Press. págs. 171–175.
4. Rice, Brian; González-Velasco, Enrique; Corrigan, Alexander (2017), "John Napier", La vida y las obras de John Napier , Springer International Publishing, p. 12, doi :10.1007/978-3-319-53282-0_1, ISBN 9783319532813
5. Napier, Mark, 1798-1879. (1834). Memorias de John Napier de Merchiston: su linaje, vida y época, con una historia de la invención de los logaritmos . W. Blackwood. pág. 67. OCLC  5167671.{{cite book}}: CS1 maint: nombres múltiples: lista de autores ( enlace ) CS1 maint: nombres numéricos: lista de autores ( enlace )
6. Havil, Julian, 1952- (5 de octubre de 2014). John Napier: vida, logaritmos y legado . Princeton. págs. 13-17. ISBN 9781400852185.OCLC 889552514  .{{cite book}}: CS1 maint: falta la ubicación del editor ( enlace ) CS1 maint: varios nombres: lista de autores ( enlace ) CS1 maint: nombres numéricos: lista de autores ( enlace )
7. Cassell's Old and New Edinburgh vol.II pág. 242.
8. Thomas Birch , Memorias de Thomas Birch , vol. 2 (Londres, 1754), págs. 28-9.
9. Caulfield, Michael J. (julio de 2010). «John Napier: His Life, His Logs, and His Bones - Introduction» (John Napier: su vida, sus registros y sus huesos: introducción). Convergencia . Washington, DC: Asociación Matemática de Estados Unidos. Archivado desde el original el 2 de mayo de 2023 . Consultado el 10 de marzo de 2019 .
10. Napier, John (1614). La descripción del maravilloso canon de logaritmos (PDF) . Traducido por Wright, Edward; Bruce, Ian. 17centurymaths.com. Archivado (PDF) del original el 22 de abril de 2023. Consultado el 14 de marzo de 2022 .
11. "17th Century Maths.com". 17centurymaths.com. 25 de marzo de 2011. Archivado desde el original el 17 de mayo de 2011. Consultado el 3 de abril de 2022 .
12. «Napier, John»  . Diccionario de biografía nacional . Londres: Smith, Elder & Co. 1885–1900.
13. Napier, John (1889) [1620]. La construcción del maravilloso canon de logaritmos . Traducido por Macdonald, William Rae. Edimburgo: Blackwood & Sons – vía Internet Archive. En los números que se distinguen así por un punto en medio, lo que se escribe después del punto es una fracción, cuyo denominador es la unidad con tantas cifras después de ella como cifras haya después del punto.
14. Molland, George. "Napier, John". Oxford Dictionary of National Biography (edición en línea). Oxford University Press. doi :10.1093/ref:odnb/19758. (Se requiere suscripción o membresía a una biblioteca pública del Reino Unido).
15. Napier, J (1614). Mirifici Logarithmorum Canonis Constructio. pag. 50. Archivado desde el original el 30 de abril de 2013 . Consultado el 14 de mayo de 2016 .Una traducción de 1889 de La construcción del maravilloso canon de logaritmos está disponible como libro electrónico en Abe Books. Archivado el 3 de marzo de 2020 en Wayback Machine.
16. Todhunter, I. (1886). Trigonometría esférica (5.ª ed.). MacMillan. Archivado desde el original el 14 de abril de 2020. Consultado el 28 de julio de 2013 .
17. Rice, Brian; González-Velasco, Enrique; Corrigan, Alexander (2017), "John Napier", La vida y las obras de John Napier , Springer International Publishing, pp. 1–60, doi :10.1007/978-3-319-53282-0_1, ISBN 9783319532813
18. "Plaine Discovery of the Whole Revelation of Saint John, obra de Napier". Encyclopædia Britannica . Consultado el 12 de junio de 2024 .
19. Un simple descubrimiento... Archivado el 7 de febrero de 2015 en Wayback Machine , Universiteitsbibliotheek Gent.
20. Arthur H. Williamson, La conciencia nacional escocesa en la época de Jacobo VI (1979), pág. 34.
21. Johnston, Ian (14 de mayo de 2005). «El genio escocés que abrió el camino a los descubrimientos de Newton». The Scotsman . Archivado desde el original el 27 de diciembre de 2005. Consultado el 29 de marzo de 2011 .
22. Springer, Will (14 de febrero de 2005). «Las raíces mágicas de Napier: artículo sobre el interés de Napier por lo oculto». The Scotsman . Archivado desde el original el 21 de octubre de 2007. Consultado el 29 de marzo de 2011 .
23. "Los huesos de Napier". Museos Nacionales de Escocia. Archivado desde el original el 24 de septiembre de 2023. Consultado el 23 de diciembre de 2017 .
24. Havil, Julian, 1952- (5 de octubre de 2014). John Napier: vida, logaritmos y legado . Princeton. pag. 21.ISBN​ 9781400852185.OCLC 889552514  .{{cite book}}: CS1 maint: falta la ubicación del editor ( enlace ) CS1 maint: varios nombres: lista de autores ( enlace ) CS1 maint: nombres numéricos: lista de autores ( enlace )
25. Havil, Julian (31 de enero de 2014). Juan Napier . Princeton: Prensa de la Universidad de Princeton. pag. 20.doi :10.1515/9781400852185 . ISBN 9781400852185.
26. Havil, Julian, 1952- (5 de octubre de 2014). John Napier: vida, logaritmos y legado . Princeton. pp. 22, 23. ISBN 9781400852185.OCLC 889552514  .{{cite book}}: CS1 maint: falta la ubicación del editor ( enlace ) CS1 maint: varios nombres: lista de autores ( enlace ) CS1 maint: nombres numéricos: lista de autores ( enlace )
27. The London encyclopaedia: or Universal dictionary of science, art, literature, and practical mechanical, including a popular view of the present state of knowledge. 1829. p. 498. Consultado el 23 de mayo de 2012 .
28. Florian Cajori (1991). Una historia de las matemáticas. American Mathematical Soc. pág. 152. ISBN 978-0-8218-2102-2. Recuperado el 23 de mayo de 2012 .
29. Ivor Grattan-Guinness (1 de agosto de 2003). Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences [Enciclopedia complementaria de la historia y la filosofía de las ciencias matemáticas]. JHU Press. pág. 1129. ISBN. 978-0-8018-7397-3. Recuperado el 23 de mayo de 2012 .
30. David Eugene Smith (1 de junio de 1958). Historia de las matemáticas . Courier Dover Publications. pág. 244. ISBN 978-0-486-20430-7. Recuperado el 23 de mayo de 2012 .
31. Garrett A. Sullivan; Alan Stewart (1 de febrero de 2012). La enciclopedia de la literatura renacentista inglesa. John Wiley & Sons. pág. 995. ISBN 978-1-4051-9449-5. Recuperado el 23 de mayo de 2012 .
32. Rice, Brian; González-Velasco, Enrique; Corrigan, Alexander (2017), "John Napier", La vida y las obras de John Napier , Springer International Publishing, p. 37, doi :10.1007/978-3-319-53282-0_1, ISBN 9783319532813
33. Neper Archivado el 16 de junio de 2010 en Wayback Machine Diccionario geográfico de nomenclatura planetaria – Astrogeología del USGS
34. Rice, Brian; González-Velasco, Enrique; Corrigan, Alexander (2017), "John Napier", La vida y las obras de John Napier , Springer International Publishing, pp. 12–14, doi :10.1007/978-3-319-53282-0_1, ISBN 9783319532813
35. Clouse, Robert G. (abril de 1974). "John Napier y el pensamiento apocalíptico". Revista del siglo XVI . 5 (1): 105. doi :10.2307/2539589. ISSN  0361-0160. JSTOR  2539589.
36. Napier, John (1889) [1619]. La construcción del maravilloso canon de logaritmos . Traducido por Macdonald, William Rae. Edimburgo: Blackwood & Sons – vía Internet Archive.

Referencias

• O'Connor, John J.; Robertson, Edmund F. , "John Napier", Archivo de Historia de las Matemáticas MacTutor , Universidad de St Andrews
• Diploudis, Alexandros. Desempolvando los huesos de Napier. Universidad Heriot-Watt, 1997
• "John Napier". Matemáticas y matemáticos: la historia de los descubrimientos matemáticos en todo el mundo. 2 vols. U*X*L, 1999
• John Napier Archivado el 8 de septiembre de 2015 en Wayback Machine Proyecto Historia de la Computación
• John Napier: breve biografía y traducción de su trabajo sobre logaritmos Archivado el 28 de diciembre de 2008 en Wayback Machine
• Introducción a la trigonometría esférica. Archivado el 29 de marzo de 2006 en Wayback Machine. Incluye un análisis del círculo de Napier y las reglas de Napier.
• EEBO (Early English Books Online) Archivado el 28 de diciembre de 2017 en Wayback Machine tiene copias electrónicas de algunos de sus trabajos, en facsímiles de ediciones de la época de Napier (se requiere suscripción o inicio de sesión en Athens)
• Mirifici logarithmorum canonis descriptio Archivado el 11 de septiembre de 2019 en Wayback Machine Descriptio De Arte Logistica Traducción al inglés por Ian Bruce

Atribución

•  Este artículo incorpora texto de una publicación que ahora es de dominio público :  «Napier, John». Dictionary of National Biography . Londres: Smith, Elder & Co. 1885–1900.

Lectura adicional

• Napier, John. La construcción del maravilloso canon de logaritmos  – vía Wikisource ., la traducción inglesa de 1889.
• Napier, Mark (1834). Memorias de John Napier de Merchiston, su linaje, vida y época, con una historia de la invención de los logaritmos. Edimburgo: William Blackwood.

Enlaces externos

• Medios relacionados con John Napier (matemático) en Wikimedia Commons
• Obras de o sobre John Napier en Wikisource
• Citas relacionadas con John Napier en Wikiquote