
Una superficie de energía potencial ( PES ) o paisaje energético describe la energía de un sistema , especialmente una colección de átomos, en términos de ciertos parámetros , normalmente las posiciones de los átomos. La superficie puede definir la energía como una función de una o más coordenadas; si solo hay una coordenada, la superficie se denomina curva de energía potencial o perfil de energía . Un ejemplo es el potencial de Morse/de largo alcance .
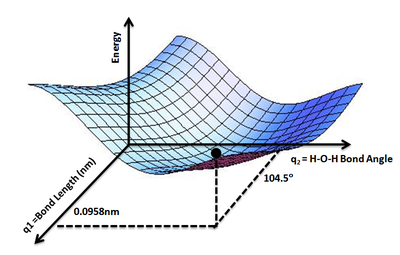
Es útil utilizar la analogía de un paisaje: para un sistema con dos grados de libertad (por ejemplo, dos longitudes de enlace), el valor de la energía (analogía: la altura del terreno) es una función de dos longitudes de enlace (analogía: las coordenadas de la posición en el suelo). [1]
El concepto PES encuentra aplicación en campos como la física , la química y la bioquímica , especialmente en las subramas teóricas de estas materias. Puede utilizarse para explorar teóricamente las propiedades de las estructuras compuestas de átomos, por ejemplo, encontrando la forma de energía mínima de una molécula o calculando las velocidades de una reacción química . Puede utilizarse para describir todas las conformaciones posibles de una entidad molecular , o las posiciones espaciales de las moléculas que interactúan en un sistema, o los parámetros y sus niveles de energía correspondientes, típicamente la energía libre de Gibbs . Geométricamente, el paisaje energético es el gráfico de la función de energía a través del espacio de configuración del sistema. El término también se utiliza de forma más general en perspectivas geométricas para la optimización matemática , cuando el dominio de la función de pérdida es el espacio de parámetros de algún sistema.
La geometría de un conjunto de átomos puede describirse mediante un vector, r , cuyos elementos representan las posiciones de los átomos. El vector r puede ser el conjunto de coordenadas cartesianas de los átomos, o también puede ser un conjunto de distancias y ángulos interatómicos.
Dado r , la energía en función de las posiciones, E ( r ) , es el valor de E ( r ) para todos los r de interés. Utilizando la analogía del paisaje de la introducción, E da la altura en el "paisaje energético", de modo que surge el concepto de una superficie de energía potencial .
Para estudiar una reacción química utilizando el PES como función de las posiciones atómicas, es necesario calcular la energía para cada disposición atómica de interés. Los métodos para calcular la energía de una disposición atómica particular de átomos están bien descritos en el artículo de química computacional , y el énfasis aquí estará en encontrar aproximaciones de E ( r ) para obtener información detallada de la posición y la energía.
Para sistemas químicos muy simples o cuando se realizan aproximaciones simplificadas sobre interacciones interatómicas, a veces es posible utilizar una expresión derivada analíticamente para la energía en función de las posiciones atómicas. Un ejemplo es el potencial de London - Eyring - Polanyi - Sato [2] [3] [4] para el sistema H + H 2 en función de las tres distancias HH.
En el caso de sistemas más complejos, el cálculo de la energía de una determinada disposición de átomos suele ser demasiado costoso desde el punto de vista computacional como para que sea posible realizar representaciones a gran escala de la superficie. Para estos sistemas, un enfoque posible es calcular solo un conjunto reducido de puntos en el PES y luego utilizar un método de interpolación computacionalmente más económico, por ejemplo, la interpolación de Shepard , para completar los espacios vacíos. [5]
Un PES es una herramienta conceptual para ayudar al análisis de la geometría molecular y la dinámica de las reacciones químicas . Una vez que se evalúan los puntos necesarios en un PES, los puntos se pueden clasificar de acuerdo con la primera y segunda derivadas de la energía con respecto a la posición, que son respectivamente el gradiente y la curvatura . Los puntos estacionarios (o puntos con un gradiente cero) tienen un significado físico: los mínimos de energía corresponden a especies químicas físicamente estables y los puntos de silla corresponden a estados de transición , el punto de energía más alto en la coordenada de reacción (que es la vía de energía más baja que conecta un reactivo químico con un producto químico).
El término es útil cuando se examina el plegamiento de proteínas ; si bien una proteína puede existir teóricamente en un número casi infinito de conformaciones a lo largo de su paisaje energético, en realidad las proteínas se pliegan (o "relajan") en estructuras secundarias y terciarias que poseen la energía libre más baja posible . El concepto clave en el enfoque del paisaje energético para el plegamiento de proteínas es la hipótesis del embudo de plegamiento .
En catálisis , al diseñar nuevos catalizadores o refinar los existentes, se consideran los paisajes energéticos para evitar intermedios de baja o alta energía que podrían detener la reacción o demandar energía excesiva para alcanzar los productos finales. [6]
En los modelos de vidrio, los mínimos locales de un paisaje energético corresponden a estados metaestables de baja temperatura de un sistema termodinámico . [7] [8]
En el aprendizaje automático , las redes neuronales artificiales pueden analizarse utilizando enfoques análogos. [9] Por ejemplo, una red neuronal puede ser capaz de ajustarse perfectamente al conjunto de entrenamiento , lo que corresponde a un mínimo global de pérdida cero, pero sobreajustando el modelo ("aprendiendo el ruido" o "memorizando el conjunto de entrenamiento"). La comprensión de cuándo sucede esto se puede estudiar utilizando la geometría del paisaje energético correspondiente. [10]
Las superficies de energía potencial para reacciones químicas pueden clasificarse como atractivas o repulsivas comparando las extensiones de las longitudes de enlace en el complejo activado en relación con las de los reactivos y productos. [11] [12] Para una reacción de tipo A + B—C → A—B + C, la extensión de la longitud de enlace para el enlace A—B recién formado se define como R* AB = R AB − R 0 AB , donde R AB es la longitud del enlace A—B en el estado de transición y R 0 AB en la molécula del producto. De manera similar, para el enlace que se rompe en la reacción, R* BC = R BC − R 0 BC , donde R 0 BC se refiere a la molécula del reactivo. [13]
Para las reacciones exotérmicas , una PES se clasifica como atractiva (o de descenso temprano ) si R* AB > R* BC , de modo que el estado de transición se alcanza mientras los reactivos se aproximan entre sí. Después del estado de transición, la longitud del enlace A—B continúa disminuyendo, de modo que gran parte de la energía de reacción liberada se convierte en energía vibracional del enlace A—B. [13] [14] Un ejemplo es la reacción del arpón K + Br 2 → K—Br + Br, en la que la atracción inicial de largo alcance de los reactivos conduce a un complejo activado que se asemeja a K + •••Br − •••Br. [13] Las poblaciones vibracionalmente excitadas de moléculas de producto se pueden detectar mediante quimioluminiscencia infrarroja . [15] [16]
En contraste, el PES para la reacción H + Cl 2 → HCl + Cl es repulsivo (o cuesta abajo tardío ) porque R* HCl < R* ClCl y el estado de transición se alcanza cuando los productos se están separando. [13] [14] Para esta reacción en la que el átomo A (aquí H) es más ligero que B y C, la energía de reacción se libera principalmente como energía cinética traslacional de los productos. [13] Para una reacción como F + H 2 → HF + H en la que el átomo A es más pesado que B y C, hay una liberación de energía mixta , tanto vibracional como traslacional, aunque el PES es repulsivo. [13]
En el caso de las reacciones endotérmicas , el tipo de superficie determina el tipo de energía más eficaz para provocar la reacción. La energía traslacional de los reactivos es más eficaz para inducir reacciones con una superficie atractiva, mientras que la excitación vibracional (a un número cuántico vibracional más alto v) es más eficaz para las reacciones con una superficie repulsiva. [13] Como ejemplo del último caso, la reacción F + HCl(v=1) → Cl + HF es aproximadamente cinco veces más rápida que F + HCl(v=0) → Cl + HF para la misma energía total de HCl. [17]
El concepto de una superficie de energía potencial para reacciones químicas fue sugerido por primera vez por el físico francés René Marcelin en 1913. [18] El primer cálculo semiempírico de una superficie de energía potencial fue propuesto para la reacción H + H 2 por Henry Eyring y Michael Polanyi en 1931. Eyring utilizó superficies de energía potencial para calcular constantes de velocidad de reacción en la teoría del estado de transición en 1935.
Las superficies de energía potencial se muestran comúnmente como gráficos tridimensionales, pero también se pueden representar mediante gráficos bidimensionales, en los que el avance de la reacción se traza mediante el uso de líneas isoenergéticas. El sistema colineal H + H 2 es una reacción simple que permite trazar una PES bidimensional de una manera fácil y comprensible. En esta reacción, un átomo de hidrógeno (H) reacciona con una molécula de dihidrógeno (H 2 ) formando un nuevo enlace con un átomo de la molécula, que a su vez rompe el enlace de la molécula original. Esto se simboliza como H a + H b –H c → H a –H b + H c . La progresión de la reacción desde los reactivos (H+H₂) hasta los productos (HHH), así como la energía de las especies que participan en la reacción, están bien definidas en la superficie de energía potencial correspondiente. Los perfiles de energía describen la energía potencial como una función de variables geométricas (las PES en cualquier dimensión son independientes del tiempo y la temperatura).

Disponemos de diferentes elementos relevantes en el PES 2-D: