grupo fundamental

Grupo matemático de las clases de homotopía de bucles en un espacio topológico.

En el campo matemático de la topología algebraica , el grupo fundamental de un espacio topológico es el grupo de las clases de equivalencia bajo homotopía de los bucles contenidos en el espacio. Registra información sobre la forma básica, o agujeros, del espacio topológico. El grupo fundamental es el primer y más simple grupo de homotopía . El grupo fundamental es un invariante de homotopía: los espacios topológicos que son equivalentes de homotopía (o el caso más fuerte de homeomórficos ) tienen grupos fundamentales isomórficos . El grupo fundamental de un espacio topológico se denota por . ${\displaystyle X}$ ${\displaystyle \pi _{1}(X)}$

Intuición

Comience con un espacio (por ejemplo, una superficie ), y algún punto en él, y todos los bucles que comienzan y terminan en este punto: caminos que comienzan en este punto, deambulan y finalmente regresan al punto de partida. Se pueden combinar dos bucles de una manera obvia: recorra el primer bucle y luego el segundo. Dos bucles se consideran equivalentes si uno puede deformarse en el otro sin romperse. El conjunto de todos esos bucles con este método de combinación y esta equivalencia entre ellos es el grupo fundamental para ese espacio en particular.

Historia

Henri Poincaré definió el grupo fundamental en 1895 en su artículo " Análisis situs ". ^[1] El concepto surgió en la teoría de las superficies de Riemann , en los trabajos de Bernhard Riemann , Poincaré y Felix Klein . Describe las propiedades de monodromía de funciones de valores complejos , además de proporcionar una clasificación topológica completa de superficies cerradas .

Definición

A lo largo de este artículo, X es un espacio topológico. Un ejemplo típico es una superficie como la que se muestra a la derecha. Además, hay un punto en X llamado punto base . (Como se explica más adelante, su función es más bien auxiliar). La idea de la definición del grupo de homotopía es medir cuántas curvas (en términos generales) en X se pueden deformar entre sí. La definición precisa depende de la noción de homotopía de bucles, que se explica primero. ${\displaystyle x_{0}}$

Homotopía de bucles

Dado un espacio topológico X , un bucle basado en ${\displaystyle x_{0}}$ se define como una función continua (también conocida como mapa continuo)

${\displaystyle \gamma \colon [0,1]\to X}$

tal que el punto inicial y el punto final sean ambos iguales a . ${\displaystyle \gamma (0)}$ ${\displaystyle \gamma (1)}$ ${\displaystyle x_{0}}$

Homotopía de bucles

Una homotopía es una interpolación continua entre dos bucles. Más precisamente, una homotopía entre dos bucles (basados ​​en el mismo punto ) es un mapa continuo ${\displaystyle \gamma ,\gamma '\colon [0,1]\to X}$ ${\displaystyle x_{0}}$

${\displaystyle h\colon [0,1]\times [0,1]\to X,}$

tal que

• ${\displaystyle h(0,t)=x_{0}}$por todo lo que es, el punto de partida de la homotopía es para todo t (que a menudo se considera un parámetro de tiempo). ${\displaystyle t\in [0,1],}$ ${\displaystyle x_{0}}$
• ${\displaystyle h(1,t)=x_{0}}$para todo lo que es, de manera similar el punto final permanece en para todo t . ${\displaystyle t\in [0,1],}$ ${\displaystyle x_{0}}$
• ${\displaystyle h(r,0)=\gamma (r),\,h(r,1)=\gamma '(r)}$para todos . ${\displaystyle r\in [0,1]}$

Si tal homotopía h existe, se dice que es homotópica . La relación " es homotópica a " es una relación de equivalencia por lo que el conjunto de clases de equivalencia puede considerarse: ${\displaystyle \gamma }$ ${\displaystyle \gamma '}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma '}$

${\displaystyle \pi _{1}(X,x_{0}):=\{{\text{all loops }}\gamma {\text{ based at }}x_{0}\}/{\text{homotopy}}}$.

Este conjunto (con la estructura de grupo que se describe a continuación) se denomina grupo fundamental del espacio topológico X en el punto base . El propósito de considerar las clases de equivalencia de bucles hasta la homotopía, a diferencia del conjunto de todos los bucles (el llamado espacio de bucles de X ) es que este último, si bien es útil para diversos propósitos, es un objeto bastante grande y difícil de manejar. . Por el contrario, el cociente anterior es, en muchos casos, más manejable y computable. ${\displaystyle x_{0}}$

Estructura de grupo

Adición de bucles

Según la definición anterior, es solo un conjunto. Se convierte en un grupo (y por tanto merece el nombre de grupo fundamental ) mediante la concatenación de bucles. Más precisamente, dados dos bucles , su producto se define como el bucle ${\displaystyle \pi _{1}(X,x_{0})}$ ${\displaystyle \gamma _{0},\gamma _{1}}$

${\displaystyle \gamma _{0}\cdot \gamma _{1}\colon [0,1]\to X}$

${\displaystyle (\gamma _{0}\cdot \gamma _{1})(t)={\begin{cases}\gamma _{0}(2t)&0\leq t\leq {\tfrac {1}{2}}\\\gamma _{1}(2t-1)&{\tfrac {1}{2}}\leq t\leq 1.\end{cases}}}$

Por lo tanto, el bucle primero sigue al bucle con "el doble de velocidad" y luego sigue con "el doble de velocidad". ${\displaystyle \gamma _{0}\cdot \gamma _{1}}$ ${\displaystyle \gamma _{0}}$ ${\displaystyle \gamma _{1}}$

El producto de dos clases de bucles de homotopía y luego se define como . Se puede demostrar que este producto no depende de la elección de los representantes y por tanto da un funcionamiento bien definido en el conjunto . Esta operación se convierte en un grupo. Su elemento neutro es el bucle constante, que permanece en todo momento t . El inverso de un bucle (clase de homotopía de a) es el mismo bucle, pero recorrido en la dirección opuesta. Más formalmente, ${\displaystyle [\gamma _{0}]}$ ${\displaystyle [\gamma _{1}]}$ ${\displaystyle [\gamma _{0}\cdot \gamma _{1}]}$ ${\displaystyle \pi _{1}(X,x_{0})}$ ${\displaystyle \pi _{1}(X,x_{0})}$ ${\displaystyle x_{0}}$

${\displaystyle \gamma ^{-1}(t):=\gamma (1-t)}$.

Dados tres bucles basados ​​en el producto ${\displaystyle \gamma _{0},\gamma _{1},\gamma _{2},}$

${\displaystyle (\gamma _{0}\cdot \gamma _{1})\cdot \gamma _{2}}$

es la concatenación de estos bucles, atravesando y luego con velocidad cuádruple, y luego con velocidad doble. En comparación, ${\displaystyle \gamma _{0}}$ ${\displaystyle \gamma _{1}}$ ${\displaystyle \gamma _{2}}$

${\displaystyle \gamma _{0}\cdot (\gamma _{1}\cdot \gamma _{2})}$

recorre los mismos caminos (en el mismo orden), pero con el doble de velocidad y con el cuádruple de velocidad. Por tanto, debido a las diferentes velocidades, los dos caminos no son idénticos. El axioma de asociatividad ${\displaystyle \gamma _{0}}$ ${\displaystyle \gamma _{1},\gamma _{2}}$

${\displaystyle [\gamma _{0}]\cdot \left([\gamma _{1}]\cdot [\gamma _{2}]\right)=\left([\gamma _{0}]\cdot [\gamma _{1}]\right)\cdot [\gamma _{2}]}$

por lo tanto, depende crucialmente del hecho de que los caminos se consideren hasta la homotopía. De hecho, los dos compuestos anteriores son homotópicos, por ejemplo, al bucle que atraviesa los tres bucles con triple velocidad. Por lo tanto, el conjunto de bucles basados ​​hasta la homotopía, equipados con la operación anterior, se convierte en un grupo. ${\displaystyle \gamma _{0},\gamma _{1},\gamma _{2}}$ ${\displaystyle \pi _{1}(X,x_{0})}$

Dependencia del punto base.

Aunque el grupo fundamental en general depende de la elección del punto base, resulta que, hasta el isomorfismo (en realidad, incluso hasta el isomorfismo interno ), esta elección no supone ninguna diferencia siempre que el espacio X esté conexo por caminos . Por lo tanto, para espacios conectados por caminos, muchos autores escriben en lugar de ${\displaystyle \pi _{1}(X)}$ ${\displaystyle \pi _{1}(X,x_{0}).}$

Ejemplos concretos

Un dominio en estrella está simplemente conectado ya que cualquier bucle puede contraerse al centro del dominio, denotado . ${\displaystyle x_{0}}$

Esta sección enumera algunos ejemplos básicos de grupos fundamentales. Para empezar, en el espacio euclidiano ( ) o cualquier subconjunto convexo de hay solo una clase de bucles de homotopía y, por tanto, el grupo fundamental es el grupo trivial con un elemento. De manera más general, cualquier dominio estelar –y aún más generalmente, cualquier espacio contráctil– tiene un grupo fundamental trivial. Por tanto, el grupo fundamental no distingue entre dichos espacios. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n},}$

Las 2 esferas

Un bucle en una esfera de 2 (la superficie de una pelota) que se contrae hasta un punto

Un espacio conexo por caminos cuyo grupo fundamental es trivial se llama simplemente conexo . Por ejemplo, las 2 esferas representadas a la derecha, y también todas las esferas de dimensiones superiores , están simplemente conectadas. La figura ilustra una homotopía que contrae un bucle particular al bucle constante. Esta idea se puede adaptar a todos los bucles tales que haya un punto que no esté en la imagen de Sin embargo, dado que hay bucles tales que (construidos a partir de la curva de Peano , por ejemplo), una demostración completa requiere un análisis más cuidadoso con herramientas de topología algebraica, como el teorema de Seifert-van Kampen o el teorema de aproximación celular . ${\displaystyle S^{2}=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid x^{2}+y^{2}+z^{2}=1\right\}}$ ${\displaystyle \gamma }$ ${\displaystyle (x,y,z)\in S^{2}}$ ${\displaystyle \gamma .}$ ${\displaystyle \gamma ([0,1])=S^{2}}$

El círculo

Elementos del grupo de homotopía del círculo.

El círculo (también conocido como 1 esfera)

${\displaystyle S^{1}=\left\{(x,y)\in \mathbb {R} ^{2}\mid x^{2}+y^{2}=1\right\}}$

no está simplemente conectado. En cambio, cada clase de homotopía consta de todos los bucles que se enrollan alrededor del círculo un número determinado de veces (que puede ser positivo o negativo, dependiendo de la dirección de enrollamiento). El producto de un bucle que gira m veces y otro que gira n veces es un bucle que gira m + n veces. Por tanto, el grupo fundamental del círculo es isomorfo al grupo aditivo de los números enteros . Este hecho se puede utilizar para demostrar el teorema del punto fijo de Brouwer ^[2] y el teorema de Borsuk-Ulam en la dimensión 2. ^[3] ${\displaystyle (\mathbb {Z} ,+),}$

la figura ocho

El grupo fundamental de la figura ocho es el grupo libre de dos generadores a y b .

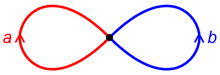
El grupo fundamental del ocho es el grupo libre de dos letras. La idea para probar esto es la siguiente: eligiendo el punto base como el punto donde se encuentran los dos círculos (punteado en negro en la imagen de la derecha), cualquier bucle se puede descomponer como ${\displaystyle \gamma }$

${\displaystyle \gamma =a^{n_{1}}b^{m_{1}}\cdots a^{n_{k}}b^{m_{k}}}$

donde a y b son los dos bucles que rodean cada mitad de la figura como se muestra, y los exponentes son números enteros. A diferencia del grupo fundamental del ocho no es abeliano : las dos formas de componer a y b no son homotópicas entre sí: ${\displaystyle n_{1},\dots ,n_{k},m_{1},\dots ,m_{k}}$ ${\displaystyle \pi _{1}(S^{1}),}$

${\displaystyle [a]\cdot [b]\neq [b]\cdot [a].}$

De manera más general, el grupo fundamental de un ramo de r círculos es el grupo libre de r letras.

El grupo fundamental de una suma de cuña de dos espacios X e Y conectados por trayectorias se puede calcular como el producto libre de los grupos fundamentales individuales:

${\displaystyle \pi _{1}(X\vee Y)\cong \pi _{1}(X)*\pi _{1}(Y).}$

Esto generaliza las observaciones anteriores ya que la figura ocho es la suma de cuña de dos círculos.

El grupo fundamental del avión perforado en n puntos es también el grupo libre con n generadores. El i -ésimo generador es la clase del bucle que rodea el i -ésimo pinchazo sin rodear ningún otro pinchazo.

Graficos

El grupo fundamental también se puede definir para estructuras discretas. En particular, considere un gráfico conexo G = ( V , E ) , con un vértice designado v ₀ en V. Los bucles en G son los ciclos que comienzan y terminan en v ₀ . ^[4] Sea T un árbol generador de G . Cada bucle simple en G contiene exactamente una arista en E \ T ; cada bucle en G es una concatenación de bucles tan simples. Por tanto, el grupo fundamental de un gráfico es un grupo libre , en el que el número de generadores es exactamente el número de aristas en E \ T . Este número es igual a | mi | − | V | + 1 . ^[5]

Por ejemplo, supongamos que G tiene 16 vértices dispuestos en 4 filas de 4 vértices cada una, con aristas que conectan vértices adyacentes horizontal o verticalmente. Entonces G tiene 24 aristas en total, y el número de aristas en cada árbol de expansión es 16 − 1 = 15 , por lo que el grupo fundamental de G es el grupo libre con 9 generadores. ^[6] Tenga en cuenta que G tiene 9 "agujeros", de forma similar a un ramo de 9 círculos, que tiene el mismo grupo fundamental.

Grupos de nudos

Un nudo de trébol .

Los grupos de nudos son, por definición, el grupo fundamental del complemento de un nudo K incrustado en.Por ejemplo, se sabe que el grupo de nudos del nudo trébol es el grupo trenzado , lo que da otro ejemplo de un grupo fundamental no abeliano. La presentación de Wirtinger describe explícitamente grupos de nudos en términos de generadores y relaciones basadas en un diagrama del nudo. Por lo tanto, los grupos de nudos tienen algún uso en la teoría de nudos para distinguir entre nudos: sino es isomorfo a algún otro grupo de nudosde otro nudo K′ , entonces K no se puede transformar en K′ . Así, el nudo trébol no puede transformarse continuamente en el círculo (también conocido como desanudado ), ya que este último tiene grupo de nudos. Sin embargo, hay nudos que no se pueden deformar entre sí, sino que tienen grupos de nudos isomórficos. ${\displaystyle \mathbb {R} ^{3}.}$ ${\displaystyle B_{3},}$ ${\displaystyle \pi _{1}(\mathbb {R} ^{3}\setminus K)}$ ${\displaystyle \pi _{1}(\mathbb {R} ^{3}\setminus K')}$ ${\displaystyle \mathbb {Z} }$

Superficies orientadas

El grupo fundamental de una superficie orientable de género n se puede calcular en términos de generadores y relaciones como

${\displaystyle \left\langle A_{1},B_{1},\ldots ,A_{n},B_{n}\left|A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}\right.\right\rangle .}$

Esto incluye al toro , siendo el caso del género 1, cuyo grupo fundamental es

${\displaystyle \left\langle A_{1},B_{1}\left|A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}\right.\right\rangle \cong \mathbb {Z} ^{2}.}$

Grupos topológicos

El grupo fundamental de un grupo topológico X (con respecto al punto base que es el elemento neutro) es siempre conmutativo. En particular, el grupo fundamental de un grupo de Lie es conmutativo. De hecho, la estructura de grupo en X dota de otra estructura de grupo: dados dos bucles y en X , se puede definir otro bucle utilizando la multiplicación de grupos en X : ${\displaystyle \pi _{1}(X)}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma '}$ ${\displaystyle \gamma \star \gamma '}$

${\displaystyle (\gamma \star \gamma ')(x)=\gamma (x)\cdot \gamma '(x).}$

Esta operación binaria sobre el conjunto de todos los bucles es a priori independiente de la descrita anteriormente. Sin embargo, el argumento de Eckmann-Hilton muestra que, de hecho, concuerda con la concatenación de bucles anterior y, además, que la estructura de grupo resultante es abeliana. ^{[7] [8]} ${\displaystyle \star }$

Una inspección de la prueba muestra que, de manera más general, es abeliano para cualquier H-espacio X , es decir, la multiplicación no necesita tener una inversa ni tiene que ser asociativa. Por ejemplo, esto muestra que el grupo fundamental de un espacio de bucle de otro espacio topológico Y , es abeliano. Ideas relacionadas conducen al cálculo de Heinz Hopf de la cohomología de un grupo de Lie . ${\displaystyle \pi _{1}(X)}$ ${\displaystyle X=\Omega (Y),}$

Funcionalidad

Si es un mapa continuo , y entonces cada bucle con punto base se puede componer para producir un bucle con punto base. Esta operación es compatible con la relación de equivalencia de homotopía y con la composición de bucles. El homomorfismo de grupo resultante , llamado homomorfismo inducido , se escribe como o, más comúnmente, ${\displaystyle f\colon X\to Y}$ ${\displaystyle x_{0}\in X}$ ${\displaystyle y_{0}\in Y}$ ${\displaystyle f(x_{0})=y_{0},}$ ${\displaystyle X}$ ${\displaystyle x_{0}}$ ${\displaystyle f}$ ${\displaystyle Y}$ ${\displaystyle y_{0}.}$ ${\displaystyle \pi (f)}$

${\displaystyle f_{*}\colon \pi _{1}(X,x_{0})\to \pi _{1}(Y,y_{0}).}$

Este mapeo de mapas continuos a homomorfismos de grupo es compatible con la composición de mapas y morfismos de identidad . En el lenguaje de la teoría de categorías , la formación de asociar a un espacio topológico su grupo fundamental es, por tanto, un funtor.

${\displaystyle {\begin{aligned}\pi _{1}\colon \mathbf {Top} _{*}&\to \mathbf {Grp} \\(X,x_{0})&\mapsto \pi _{1}(X,x_{0})\end{aligned}}}$

de la categoría de espacios topológicos junto con un punto base a la categoría de grupos . Resulta que este functor no distingue aplicaciones que son homotópicas con respecto al punto base: si son aplicaciones continuas con , y f y g son homotópicas con respecto a { x ₀ }, entonces f _∗ = g _∗ . Como consecuencia, dos espacios conectados por caminos equivalentes de homotopía tienen grupos fundamentales isomórficos: ${\displaystyle f,g:X\to Y}$ ${\displaystyle f(x_{0})=g(x_{0})=y_{0}}$

${\displaystyle X\simeq Y\implies \pi _{1}(X,x_{0})\cong \pi _{1}(Y,y_{0}).}$

Por ejemplo, la inclusión del círculo en el plano perforado.

${\displaystyle S^{1}\subset \mathbb {R} ^{2}\setminus \{0\}}$

es una equivalencia de homotopía y por lo tanto produce un isomorfismo de sus grupos fundamentales.

El funtor de grupo fundamental lleva productos a productos y coproductos a coproductos . Es decir, si X e Y están conectados por caminos, entonces

${\displaystyle \pi _{1}(X\times Y,(x_{0},y_{0}))\cong \pi _{1}(X,x_{0})\times \pi _{1}(Y,y_{0})}$

y si también son contraíbles localmente , entonces

${\displaystyle \pi _{1}(X\vee Y)\cong \pi _{1}(X)*\pi _{1}(Y).}$

(En la última fórmula, denota la suma de cuña de espacios topológicos puntiagudos y el producto libre de grupos). La última fórmula es un caso especial del teorema de Seifert-van Kampen , que establece que el funtor de grupo fundamental toma expulsiones a lo largo de inclusiones para expulsiones. ${\displaystyle \vee }$ ${\displaystyle *}$

Resultados abstractos

Como se mencionó anteriormente, calcular el grupo fundamental incluso de espacios topológicos relativamente simples tiende a no ser del todo trivial, pero requiere algunos métodos de topología algebraica .

Relación con el primer grupo de homología

La abelianización del grupo fundamental se puede identificar con el primer grupo de homología del espacio.

Un caso especial del teorema de Hurewicz afirma que el primer grupo de homología singular es, coloquialmente hablando, la aproximación más cercana al grupo fundamental mediante un grupo abeliano. Con más detalle, mapear la clase de homotopía de cada bucle con la clase de homología del bucle da un homomorfismo de grupo. ${\displaystyle H_{1}(X)}$

${\displaystyle \pi _{1}(X)\to H_{1}(X)}$

desde el grupo fundamental de un espacio topológico X hasta su primer grupo de homología singular. Este homomorfismo no es en general un isomorfismo ya que el grupo fundamental puede ser no abeliano, pero el grupo de homología es, por definición, siempre abeliano. Sin embargo, esta diferencia es la única: si X es conexo por caminos, este homomorfismo es sobreyectivo y su núcleo es el subgrupo conmutador del grupo fundamental, por lo que es isomorfo a la abelianización del grupo fundamental. ^[9] ${\displaystyle H_{1}(X).}$ ${\displaystyle H_{1}(X)}$

Pegado de espacios topológicos

Generalizando la afirmación anterior, para una familia de espacios conexos de caminos, el grupo fundamental es el producto libre de los grupos fundamentales de ^[10] Este hecho es un caso especial del teorema de Seifert-van Kampen , que permite calcular, de manera más general, grupos fundamentales de espacios que se pegan entre sí desde otros espacios. Por ejemplo, las 2 esferas se pueden obtener pegando dos copias de medias esferas ligeramente superpuestas a lo largo de una vecindad del ecuador . En este caso el resultado del teorema es trivial, ya que las dos semiesferas son contráctiles y por tanto tienen un grupo fundamental trivial. Los grupos fundamentales de superficies, como se mencionó anteriormente, también se pueden calcular usando este teorema. ${\displaystyle X_{i},}$ ${\textstyle \pi _{1}\left(\bigvee _{i\in I}X_{i}\right)}$ ${\displaystyle X_{i}.}$ ${\displaystyle S^{2}}$ ${\displaystyle \pi _{1}(S^{2})}$

En el lenguaje de la teoría de categorías, el teorema se puede expresar de manera concisa diciendo que el functor de grupo fundamental toma expulsiones (en la categoría de espacios topológicos) a lo largo de inclusiones hasta expulsiones (en la categoría de grupos). ^[11]

Revestimientos

El mapa es una cobertura: la preimagen de U ( resaltada en gris) es una unión inconexa de copias de U. Además, es una cobertura universal ya que es contraíble y por tanto de fácil conexión. ${\displaystyle \mathbb {R} \times [0,1]\to S^{1}\times [0,1]}$ ${\displaystyle \mathbb {R} \times [0,1]}$

Dado un espacio topológico B , un mapa continuo

${\displaystyle f:E\to B}$

se llama cobertura o E se llama espacio de cobertura de B si cada punto b en B admite una vecindad abierta U tal que existe un homeomorfismo entre la preimagen de U y una unión disjunta de copias de U (indexada por algún conjunto I ) ,

${\displaystyle \varphi :\bigsqcup _{i\in I}U\to f^{-1}(U)}$

de tal manera que sea el mapa de proyección estándar ^[12] ${\displaystyle \pi \circ \varphi }$ ${\displaystyle \bigsqcup _{i\in I}U\to U.}$

Revestimiento universal

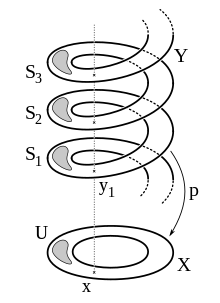
Una cubierta se llama cubierta universal si E , además de la condición anterior, es simplemente conexa. ^[13] Es universal en el sentido de que todas las demás coberturas pueden construirse identificando adecuadamente los puntos en E. Conociendo una cobertura universal

${\displaystyle p:{\widetilde {X}}\to X}$

de un espacio topológico X es útil para comprender su grupo fundamental de varias maneras: primero, se identifica con el grupo de transformaciones de deck , es decir, el grupo de homeomorfismos que conmutan con el mapa de X , es decir, otra relación con el grupo fundamental es que Se puede identificar con la fibra. Por ejemplo, el mapa. ${\displaystyle \pi _{1}(X)}$ ${\displaystyle \varphi :{\widetilde {X}}\to {\widetilde {X}}}$ ${\displaystyle p\circ \varphi =p.}$ ${\displaystyle \pi _{1}(X,x)}$ ${\displaystyle p^{-1}(x).}$

${\displaystyle p:\mathbb {R} \to S^{1},\,t\mapsto \exp(2\pi it)}$

(o, de manera equivalente, ) es una cobertura universal. Las transformaciones de la plataforma son los mapas de Esto está en línea con la identificación en particular, esto prueba la afirmación anterior. ${\displaystyle \pi :\mathbb {R} \to \mathbb {R} /\mathbb {Z} ,\ t\mapsto [t]}$ ${\displaystyle t\mapsto t+n}$ ${\displaystyle n\in \mathbb {Z} .}$ ${\displaystyle p^{-1}(1)=\mathbb {Z} ,}$ ${\displaystyle \pi _{1}(S^{1})\cong \mathbb {Z} .}$

Cualquier camino conectado, camino conectado localmente y espacio topológico X simplemente conectado localmente admite una cobertura universal. ^[14] Una construcción abstracta procede de manera análoga al grupo fundamental tomando pares ( x , γ), donde x es un punto en X y γ es una clase de homotopía de caminos de x ₀ a x . El paso de un espacio topológico a su cobertura universal puede utilizarse para comprender la geometría de X. Por ejemplo, el teorema de uniformización muestra que cualquier superficie de Riemann simplemente conectada es (isomorfa a) cualquiera de los dos o el semiplano superior . ^[15] Las superficies generales de Riemann surgen entonces como cocientes de acciones grupales sobre estas tres superficies. ${\displaystyle S^{2},}$ ${\displaystyle \mathbb {C} ,}$

El cociente de una acción libre de un grupo discreto G sobre un espacio simplemente conexo Y tiene grupo fundamental

${\displaystyle \pi _{1}(Y/G)\cong G.}$

Como ejemplo, el espacio proyectivo real de n dimensiones se obtiene como el cociente de la esfera unitaria de n dimensiones por la acción antípoda del grupo que envía a As es simplemente conexo para n ≥ 2, es una cobertura universal de en estos casos, lo que implica para n ≥ 2. ${\displaystyle \mathbb {R} \mathrm {P} ^{n}}$ ${\displaystyle S^{n}}$ ${\displaystyle \mathbb {Z} /2}$ ${\displaystyle x\in S^{n}}$ ${\displaystyle -x.}$ ${\displaystyle S^{n}}$ ${\displaystyle \mathbb {R} \mathrm {P} ^{n}}$ ${\displaystyle \pi _{1}(\mathbb {R} \mathrm {P} ^{n})\cong \mathbb {Z} /2}$

grupos de mentiras

Sea G un grupo de Lie compacto conexo, simplemente conexo , por ejemplo, el grupo unitario especial SU( n ), y sea Γ un subgrupo finito de G. Entonces el espacio homogéneo X  =  G /Γ tiene grupo fundamental Γ, que actúa por multiplicación recta sobre el espacio de cobertura universal G . Entre las muchas variantes de esta construcción, una de las más importantes está dada por los espacios localmente simétricos X  = Γ \ G / K , donde

• G es un grupo de Lie conectado, no compacto, simplemente conectado (a menudo semisimple ),
• K es un subgrupo compacto máximo de G
• Γ es un subgrupo discreto contable y libre de torsión de G .

En este caso, el grupo fundamental es Γ y el espacio de cobertura universal G / K es en realidad contráctil (mediante la descomposición de Cartan para grupos de Lie).

Como ejemplo, tomemos G  = SL(2, R ), K  = SO(2) y Γ cualquier subgrupo de congruencia libre de torsión del grupo modular SL(2, Z ).

De la realización explícita, también se deduce que el espacio de cobertura universal de un grupo topológico conectado por caminos H es nuevamente un grupo topológico conectado por caminos G. Además, el mapa de cobertura es un homomorfismo abierto continuo de G sobre H con núcleo Γ, un subgrupo normal discreto cerrado de G :

${\displaystyle 1\to \Gamma \to G\to H\to 1.}$

Dado que G es un grupo conexo con una acción continua por conjugación sobre un grupo discreto Γ, debe actuar de manera trivial, por lo que Γ tiene que ser un subgrupo del centro de G. En particular π ₁ ( H ) = Γ es un grupo abeliano ; esto también se puede ver fácilmente directamente sin utilizar espacios de cobertura. El grupo G se llama grupo de cobertura universal de  H.

Como sugiere el grupo de cobertura universal, existe una analogía entre el grupo fundamental de un grupo topológico y el centro de un grupo; esto se elabora en Celosía de grupos de cobertura .

Fibraciones

Las fibraciones proporcionan un medio muy poderoso para calcular grupos de homotopía. Una fibración del llamado espacio total y del espacio base B tiene, en particular, la propiedad de que todas sus fibrasson equivalentes en homotopía y, por tanto, no pueden distinguirse utilizando grupos fundamentales (y grupos de homotopía superiores), siempre que B sea un camino -conectado. ^[16] Por lo tanto, el espacio E puede considerarse como un " producto retorcido " del espacio base B y la fibra. La gran importancia de las fibraciones para el cálculo de grupos de homotopía proviene de una secuencia larga y exacta. ${\displaystyle f^{-1}(b)}$ ${\displaystyle F=f^{-1}(b).}$

${\displaystyle \dots \to \pi _{2}(B)\to \pi _{1}(F)\to \pi _{1}(E)\to \pi _{1}(B)\to \pi _{0}(F)\to \pi _{0}(E)}$

siempre que B esté conectado por camino. ^[17] El término es el segundo grupo de homotopía de B , que se define como el conjunto de clases de homotopía de aplicaciones desde a B , en directa analogía con la definición de ${\displaystyle \pi _{2}(B)}$ ${\displaystyle S^{2}}$ ${\displaystyle \pi _{1}.}$

Si E resulta ser conexo por caminos y simplemente conexo, esta secuencia se reduce a un isomorfismo

${\displaystyle \pi _{1}(B)\cong \pi _{0}(F)}$

lo que generaliza el hecho anterior sobre la cobertura universal (que equivale al caso en el que la fibra F también es discreta). Si, en cambio, F resulta ser conexo y simplemente conexo, se reduce a un isomorfismo

${\displaystyle \pi _{1}(E)\cong \pi _{1}(B).}$

Es más, la secuencia puede continuar a la izquierda con los grupos de homotopía más altos de los tres espacios, lo que da cierto acceso a calcular dichos grupos en la misma línea. ${\displaystyle \pi _{n}}$

Grupos de mentira clásica

Estas secuencias de fibras se pueden utilizar para calcular inductivamente grupos fundamentales de grupos de Lie clásicos compactos , como el grupo unitario especial con Este grupo actúa transitivamente sobre la esfera unitaria interior El estabilizador de un punto en la esfera es isomorfo a Entonces se puede demostrar ^{[18 ]} que esto produce una secuencia de fibras ${\displaystyle \mathrm {SU} (n),}$ ${\displaystyle n\geq 2.}$ ${\displaystyle S^{2n-1}}$ ${\displaystyle \mathbb {C} ^{n}=\mathbb {R} ^{2n}.}$ ${\displaystyle \mathrm {SU} (n-1).}$

${\displaystyle \mathrm {SU} (n-1)\to \mathrm {SU} (n)\to S^{2n-1}.}$

Dado que la esfera tiene dimensión al menos 3, lo que implica ${\displaystyle n\geq 2,}$ ${\displaystyle S^{2n-1}}$

${\displaystyle \pi _{1}(S^{2n-1})\cong \pi _{2}(S^{2n-1})=1.}$

La larga secuencia exacta muestra entonces un isomorfismo

${\displaystyle \pi _{1}(\mathrm {SU} (n))\cong \pi _{1}(\mathrm {SU} (n-1)).}$

Dado que es un solo punto, eso es trivial, esto muestra que es simplemente conexo para todos ${\displaystyle \mathrm {SU} (1)}$ ${\displaystyle \pi _{1}(\mathrm {SU} (1))}$ ${\displaystyle \mathrm {SU} (n)}$ ${\displaystyle n.}$

El grupo fundamental de grupos de Lie no compactos se puede reducir al caso compacto, ya que dicho grupo es homotópico a su subgrupo compacto máximo. ^[19] Estos métodos dan los siguientes resultados: ^[20]

Un segundo método para calcular grupos fundamentales se aplica a todos los grupos de Lie compactos conectados y utiliza la maquinaria del toro máximo y el sistema de raíces asociado . Específicamente, sea un toro máximo en un grupo de Lie compacto conectado y sea el álgebra de Lie del mapa exponencial ${\displaystyle T}$ ${\displaystyle K,}$ ${\displaystyle {\mathfrak {t}}}$ ${\displaystyle T.}$

${\displaystyle \exp :{\mathfrak {t}}\to T}$

es una fibración y por lo tanto su núcleo se identifica con The map ${\displaystyle \Gamma \subset {\mathfrak {t}}}$ ${\displaystyle \pi _{1}(T).}$

${\displaystyle \pi _{1}(T)\to \pi _{1}(K)}$

Se puede demostrar que es sobreyectivo ^[21] con el núcleo dado por el conjunto I de combinación lineal entera de raíces . Esto lleva al cálculo

${\displaystyle \pi _{1}(K)\cong \Gamma /I.}$^[22]

Este método muestra, por ejemplo, que cualquier grupo de Lie compacto conectado para el cual el sistema raíz asociado sea del tipo ${\displaystyle G_{2}}$ está simplemente conectado. ^[23] Por lo tanto, hay (hasta el isomorfismo) sólo un grupo de Lie compacto conectado que tiene álgebra de Lie de tipo ; este grupo es simplemente conexo y tiene centro trivial. ${\displaystyle G_{2}}$

Grupo de ruta de borde de un complejo simplicial

Cuando el espacio topológico es homeomorfo a un complejo simplicial , su grupo fundamental puede describirse explícitamente en términos de generadores y relaciones .

Si X es un complejo simplicial conectado , una ruta de borde en X se define como una cadena de vértices conectados por aristas en X. Se dice que dos trayectorias de aristas son equivalentes a aristas si una se puede obtener a partir de la otra cambiando sucesivamente entre una arista y las dos aristas opuestas de un triángulo en X. Si v es un vértice fijo en X , un bucle de borde en v es una ruta de borde que comienza y termina en v . El grupo de ruta de borde E ( X ,  v ) se define como el conjunto de clases de equivalencia de borde de bucles de borde en v , con el producto y la inversa definidos por la concatenación e inversión de bucles de borde.

El grupo de trayectoria de borde es naturalmente isomorfo a π ₁ (| X  |,  v ), el grupo fundamental de la realización geométrica | X  | de X. _ ^[24] Dado que depende sólo del 2-esqueleto X ² de X (es decir, los vértices, aristas y triángulos de X ), los grupos π ₁ (| X  |, v ) y π ₁ (| X ² | ,  v ) son isomorfos.

El grupo de ruta de borde se puede describir explícitamente en términos de generadores y relaciones . Si T es un árbol de expansión máximo en el esqueleto 1 de X , entonces E ( X ,  v ) es canónicamente isomorfo al grupo con generadores (las rutas de borde orientadas de X que no ocurren en T ) y relaciones (las equivalencias de borde correspondiente a triángulos en X ). Un resultado similar se cumple si T se reemplaza por cualquier subcomplejo simplemente conexo , en particular contráctil , de X. Esto a menudo proporciona una forma práctica de calcular grupos fundamentales y puede usarse para mostrar que cada grupo presentado finitamente surge como el grupo fundamental de un complejo simplicial finito. También es uno de los métodos clásicos utilizados para superficies topológicas , las cuales se clasifican por sus grupos fundamentales.

El espacio de cobertura universal de un complejo simplicial finito conectado X también se puede describir directamente como un complejo simplicial utilizando caminos de borde. Sus vértices son pares ( w , γ ) donde w es un vértice de X y γ es una clase de caminos de equivalencia de aristas de v a w . Los k -símplices que contienen ( w ,γ ) corresponden naturalmente a los k -símplices que contienen w . Cada nuevo vértice u del k -simplex da una arista wu y por tanto, por concatenación, un nuevo camino γ _u desde v hasta u . Los puntos ( w , γ ) y ( u , γ _u ) son los vértices del simplex "transportado" en el espacio de cobertura universal. El grupo de ruta de borde actúa naturalmente mediante concatenación, preservando la estructura simplicial, y el espacio cociente es solo X.

Es bien sabido que este método también se puede utilizar para calcular el grupo fundamental de un espacio topológico arbitrario. Esto sin duda lo sabían Eduard Čech y Jean Leray y apareció explícitamente como comentario en un artículo de André Weil ; ^[25] Varios otros autores como Lorenzo Calabi, Wu Wen-tsün y Nodar Berikashvili también han publicado pruebas. En el caso más simple de un espacio compacto X con una cobertura abierta finita en el que todas las intersecciones finitas no vacías de conjuntos abiertos en la cobertura son contráctiles, el grupo fundamental se puede identificar con el grupo de caminos de borde del complejo simplicial correspondiente al Nervio de la cubierta .

Realizabilidad

• Cada grupo puede realizarse como el grupo fundamental de un complejo CW conectado de dimensión 2 (o superior). Sin embargo, como se señaló anteriormente, solo los grupos libres pueden ocurrir como grupos fundamentales de complejos CW unidimensionales (es decir, gráficos).
• Cada grupo presentado finitamente puede realizarse como el grupo fundamental de una variedad compacta , conectada y suave de dimensión 4 (o superior). Pero existen severas restricciones sobre qué grupos ocurren como grupos fundamentales de variedades de baja dimensión. Por ejemplo, ningún grupo abeliano libre de rango 4 o superior puede realizarse como grupo fundamental de una variedad de dimensión 3 o menos. Se puede demostrar que cada grupo puede considerarse como el grupo fundamental de un espacio compacto de Hausdorff si y sólo si no existe un cardinal mensurable . ^[26]

Conceptos relacionados

Grupos de mayor homotopía

En términos generales, el grupo fundamental detecta la estructura de agujeros unidimensionales de un espacio, pero no los agujeros en dimensiones superiores, como en el caso de las 2 esferas. Estos "agujeros de dimensiones superiores" se pueden detectar utilizando los grupos de homotopía superior, que se definen como clases de homotopía de mapas (que preservan el punto de base) desde a X. Por ejemplo, el teorema de Hurewicz implica que para todo el n -ésimo grupo de homotopía de la n -esfera es ${\displaystyle \pi _{n}(X)}$ ${\displaystyle S^{n}}$ ${\displaystyle n\geq 1}$

${\displaystyle \pi _{n}(S^{n})=\mathbb {Z} .}$^[27]

Como se mencionó en el cálculo anterior de los grupos de Lie clásicos, los grupos de homotopía superior pueden ser relevantes incluso para calcular grupos fundamentales. ${\displaystyle \pi _{1}}$

Espacio de bucle

El conjunto de bucles basados ​​(tal cual, es decir, no llevados a la homotopía) en un espacio puntiagudo X , dotado de topología abierta compacta , se conoce como espacio de bucles , denotado como el grupo fundamental de X está en biyección con el conjunto de caminos. componentes de su espacio de bucle: ^[28] ${\displaystyle \Omega X.}$

${\displaystyle \pi _{1}(X)\cong \pi _{0}(\Omega X).}$

grupoide fundamental

El grupoide fundamental es una variante del grupo fundamental que resulta útil en situaciones en las que la elección de un punto base no es deseable. Se define considerando primero la categoría de caminos , es decir, funciones continuas ${\displaystyle x_{0}\in X}$ ${\displaystyle X,}$

${\displaystyle \gamma \colon [0,r]\to X}$,

donde r es un número real arbitrario no negativo. Dado que la longitud r es variable en este enfoque, dichos caminos pueden concatenarse tal como están (es decir, sin alcanzar la homotopía) y, por lo tanto, producen una categoría. ^[29] Dos de estos caminos con los mismos puntos finales y longitud r , resp. r' se consideran equivalentes si existen números reales tales que y son homotópicos con respecto a sus puntos finales, donde ^{[30] [31]} ${\displaystyle \gamma ,\gamma '}$ ${\displaystyle u,v\geqslant 0}$ ${\displaystyle r+u=r'+v}$ ${\displaystyle \gamma _{u},\gamma '_{v}\colon [0,r+u]\to X}$ ${\displaystyle \gamma _{u}(t)={\begin{cases}\gamma (t),&t\in [0,r]\\\gamma (r),&t\in [r,r+u].\end{cases}}}$

La categoría de caminos hasta esta relación de equivalencia se denota. Cada morfismo es un isomorfismo , con la inversa dada por el mismo camino recorrido en la dirección opuesta. Esta categoría se llama grupoide . Reproduce el grupo fundamental ya que ${\displaystyle \Pi (X).}$ ${\displaystyle \Pi (X)}$

${\displaystyle \pi _{1}(X,x_{0})=\mathrm {Hom} _{\Pi (X)}(x_{0},x_{0})}$.

De manera más general, se puede considerar el grupoide fundamental sobre un conjunto A de puntos base, elegidos según la geometría de la situación; por ejemplo, en el caso del círculo, que se puede representar como la unión de dos conjuntos abiertos conectados cuya intersección tiene dos componentes, se puede elegir un punto base en cada componente. El teorema de van Kampen admite una versión para grupoides fundamentales que proporciona, por ejemplo, otra forma de calcular el grupo fundamental (oide) de ^[32] ${\displaystyle S^{1}.}$

Sistemas locales

En términos generales, las representaciones pueden servir para exhibir características de un grupo mediante sus acciones sobre otros objetos matemáticos, a menudo espacios vectoriales . Las representaciones del grupo fundamental tienen un significado muy geométrico: cualquier sistema local (es decir, un haz en X con la propiedad de que localmente en una vecindad U suficientemente pequeña de cualquier punto en X , la restricción de F es un haz constante de la forma ) da lugar a la llamada representación monodromía, una representación del grupo fundamental en un espacio vectorial de n dimensiones . Por el contrario , cualquier representación de este tipo en un espacio X conectado por un camino surge de esta manera. ^[33] Esta equivalencia de categorías entre representaciones de y sistemas locales se utiliza, por ejemplo, en el estudio de ecuaciones diferenciales , como las ecuaciones de Knizhnik-Zamolodchikov . ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}|_{U}=\mathbb {Q} ^{n}}$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \pi _{1}(X)}$

grupo fundamental étale

En geometría algebraica , el llamado grupo fundamental étale se utiliza como reemplazo del grupo fundamental. ^[34] Dado que la topología de Zariski en una variedad algebraica o esquema X es mucho más burda que, digamos, la topología de subconjuntos abiertos, ya no tiene sentido considerar aplicaciones continuas desde un intervalo hasta X. En cambio, el enfoque desarrollado por Grothendieck consiste en construir considerando todas las cubiertas de étale finitas de X. Éstos sirven como un análogo álgebro-geométrico de los revestimientos con fibras finitas. ${\displaystyle \mathbb {R} ^{n},}$ ${\displaystyle \pi _{1}^{\text{et}}}$

Esto produce una teoría aplicable en situaciones en las que no se dispone de intuición topológica clásica de gran generalidad, por ejemplo, para variedades definidas en un campo finito . Además, el grupo fundamental étale de un campo es su grupo de Galois ( absoluto ) . Por otro lado, para variedades suaves X sobre números complejos, el grupo fundamental étale retiene gran parte de la información inherente al grupo fundamental clásico: el primero es la terminación finita del segundo. ^[35]

Grupo fundamental de grupos algebraicos.

Se define el grupo fundamental de un sistema de raíces , de forma análoga al cálculo de los grupos de Lie. ^[36] Esto permite definir y utilizar el grupo fundamental de un grupo algebraico lineal semisimple G , que es una herramienta básica útil en la clasificación de grupos algebraicos lineales. ^[37]

Grupo fundamental de conjuntos simpliciales.

La relación de homotopía entre 1-simplices de un conjunto simplicial X es una relación de equivalencia si X es un complejo de Kan , pero no necesariamente así en general. ^[38] Por lo tanto, un complejo de Kan se puede definir como el conjunto de clases de homotopía de 1-símplices. El grupo fundamental de un conjunto simplicial arbitrario X se define como el grupo de homotopía de su realización topológica, es decir, el espacio topológico obtenido pegando simplices topológicos según lo prescrito por la estructura del conjunto simplicial de X. ^[39] ${\displaystyle \pi _{1}}$ ${\displaystyle |X|,}$

Ver también

• Grupo fundamental Orbifold
• Esquema de grupo fundamental

Notas

1. Poincaré, Henri (1895). "Análisis situs". Revista de la Escuela Politécnica . (2) (en francés). 1 : 1–123.Traducido en Poincaré, Henri (2009). «Análisis situs» (PDF) . Artículos sobre topología: análisis situs y sus cinco suplementos . Traducido por John Stillwell . págs. 18–99. Archivado (PDF) desde el original el 27 de marzo de 2012.
2. Mayo (1999, capítulo 1, §6)
3. Massey (1991, capítulo V, §9)
4. "Significado del grupo fundamental de un gráfico". Intercambio de pilas de matemáticas . Consultado el 28 de julio de 2020 .
5. Simón, J (2008). «Ejemplo de cálculo del grupo fundamental de un gráfico G» (PDF) . Archivado (PDF) desde el original el 28 de julio de 2020.
6. "Los grupos fundamentales de gráficos conectados - Mathonline". mathonline.wikidot.com . Consultado el 28 de julio de 2020 .
7. Strom (2011, Problema 9.30, 9.31), Hall (2015, Ejercicio 13.7)
8. Prueba: Dados dos bucles en defina el mapeo multiplicado puntualmente en Considere la familia de caminos homotópicos en el rectángulo desde hasta que comienza con el camino horizontal y luego vertical, se mueve a través de varios caminos diagonales y termina con el camino vertical y luego vertical. camino horizontal. Componer esta familia da una homotopía que muestra que el grupo fundamental es abeliano. ${\displaystyle \alpha ,\beta :[0,1]\to G}$ ${\displaystyle \pi _{1}(G),}$ ${\displaystyle A\colon [0,1]\times [0,1]\to G}$ ${\displaystyle A(s,t)=\alpha (s)\cdot \beta (t),}$ ${\displaystyle G.}$ ${\displaystyle (s,t)=(0,0)}$ ${\displaystyle (1,1)}$ ${\displaystyle A}$ ${\displaystyle \alpha *\beta \sim \beta *\alpha ,}$
9. Fulton (1995, propuesta 12.22)
10. Mayo (1999, capítulo 2, §8, propuesta)
11. Mayo (1999, capítulo 2, §7)
12. Hatcher (2002, §1.3)
13. Hatcher (2002, pág.65)
14. Hatcher (2002, Proposición 1.36)
15. Forster (1981, teorema 27.9)
16. Hatcher (2002, propuesta 4.61)
17. Hatcher (2002, teorema 4.41)
18. Salón (2015, Proposición 13.8)
19. Salón (2015, Sección 13.3)
20. Salón (2015, Proposición 13.10)
21. Golpe (2013, Proposición 23.7)
22. Salón (2015, Corolario 13.18)
23. Salón (2015, ejemplo 13.45)
24. Cantante, Isadore ; Thorpe, John A. (1967). Apuntes de conferencias sobre topología y geometría elementales . Springer-Verlag. pag. 98.ISBN _ 0-387-90202-3.
25. André Weil , Sobre subgrupos discretos de grupos de Lie , Annals of Mathematics 72 (1960), 369-384.
26. Adam Przezdziecki, Cardenales mensurables y grupos fundamentales de espacios compactos, Fundamenta Mathematicae 192 (2006), 87-92 [1]
27. Hatcher (2002, §4.1)
28. Adams (1978, pág.5)
29. Marrón (2006, §6.1)
30. Marrón (2006, §6.2)
31. Crowell y Fox (1963) utilizan una definición diferente al reparar los caminos a la longitud 1 .
32. Marrón (2006, §6.7)
33. El Zein et al. (2010, pág. 117, Proposición 1.7)
34. Grothendieck y Raynaud (2003).
35. Grothendieck y Raynaud (2003, Exposé XII, Cor. 5.2).
36. Humphreys (1972, §13.1)
37. Humphreys (2004, §31.1)
38. Goerss y Jardine (1999, §I.7)
39. Goerss y Jardine (1999, §I.11)

Referencias

• Adams, John Frank (1978), Espacios de bucle infinito , Annals of Mathematics Studies, vol. 90, Prensa de la Universidad de Princeton , ISBN 978-0-691-08207-3, señor  0505692
• Brown, Ronald (2006), Topología y grupoides, Booksurge, ISBN 1-4196-2722-8
• Bump, Daniel (2013), Grupos de mentiras , Textos de Posgrado en Matemáticas, vol. 225 (2ª ed.), Springer, doi :10.1007/978-1-4614-8024-2, ISBN 978-1-4614-8023-5
• Crowell, Richard H.; Fox, Ralph (1963), Introducción a la teoría de nudos , Springer
• El Zein, Fouad; Suciu, Alejandro I.; Tosun, Meral; Uludağ, Mahoma; Yuzvinsky, Sergey (2010), Arreglos, sistemas locales y singularidades: Escuela de verano CIMPA, Universidad Galatasaray, Estambul, 2007 , ISBN 978-3-0346-0208-2
• Forster, Otto (1981), Conferencias sobre superficies de Riemann , ISBN 0-387-90617-7
• Fulton, William (1995), Topología algebraica: un primer curso , Springer, ISBN 9780387943275
• Goerss, Paul G.; Jardine, John F. (1999), Teoría de la homotopía simple , Progreso en Matemáticas, vol. 174, Basilea, Boston, Berlín: Birkhäuser, ISBN 978-3-7643-6064-1
• Grothendieck, Alejandro ; Raynaud, Michèle (2003) [1971], Séminaire de Géométrie Algébrique du Bois Marie - 1960-61 - Revêtements étales et groupe fondamental - (SGA 1) (Documents Mathématiques 3 ) , París: Société Mathématique de France , págs. xviii+327 , ver exp. V, IX, X, arXiv : math.AG/0206203 , ISBN 978-2-85629-141-2
• Hall, Brian C. (2015), Grupos de mentiras, álgebras de mentiras y representaciones: una introducción elemental , Textos de posgrado en matemáticas, vol. 222 (2ª ed.), Springer, ISBN 978-3319134666
• Hatcher, Allen (2002), Topología algebraica, Cambridge University Press, ISBN 0-521-79540-0
• Peter Hilton y Shaun Wylie , Homology Theory , Cambridge University Press (1967) [advertencia: estos autores utilizan contrahomología para cohomología ]
• Humphreys, James E. (2004), Grupos algebraicos lineales , Textos de posgrado en matemáticas, Springer, ISBN 9780387901084
• Humphreys, James E. (1972), Introducción a las álgebras de mentiras y la teoría de la representación , ISBN 0-387-90052-7
• Maunder, CRF (enero de 1996), Topología algebraica , Publicaciones de Dover , ISBN 0-486-69131-4
• Massey, William S. (1991), Un curso básico en topología algebraica , Springer, ISBN 038797430X
• May, J. Peter (1999), Un curso conciso en topología algebraica , ISBN 9780226511832
• Deane Montgomery y Leo Zippin, Grupos de transformación topológica , Interscience Publishers (1955)
• Munkres, James R. (2000), Topología , Prentice Hall , ISBN 0-13-181629-2
• Rotman, Joseph (22 de julio de 1998), Introducción a la topología algebraica , Springer-Verlag , ISBN 0-387-96678-1
• Rubei, Elena (2014), Geometría algebraica, un diccionario conciso , Berlín/Boston: Walter De Gruyter, ISBN 978-3-11-031622-3
• Seifert, Herbert ; Threlfall, William (1980), Un libro de texto de topología , traducido por Heil, Wolfgang, Academic Press , ISBN 0-12-634850-2
• Cantante, Isadore. M. ; Thorpe, JA (10 de diciembre de 1976), Apuntes de conferencias sobre topología y geometría elementales , ISBN 0-387-90202-3
• Spanier, Edwin H. (1989), Topología algebraica , Springer, ISBN 0-387-94426-5
• Strom, Jeffrey (2011), Teoría de la homotopía clásica moderna , AMS, ISBN 9780821852866

enlaces externos

• Weisstein, Eric W. "Grupo fundamental". MundoMatemático .
• Dylan GL Allegretti, Conjuntos simpliciales y teorema de van Kampen: una discusión sobre el grupoide fundamental de un espacio topológico y el grupoide fundamental de un conjunto simplicial
• Animaciones para presentar el grupo fundamental de Nicolas Delanoue.
• Conjuntos de puntos base y grupoides fundamentales: discusión de mathoverflow
• Grupoides en matemáticas