En lógica proposicional , una fórmula proposicional es un tipo de fórmula sintáctica que está bien formada y tiene un valor de verdad . Si se dan los valores de todas las variables en una fórmula proposicional, se determina un valor de verdad único. Una fórmula proposicional también puede denominarse expresión proposicional , oración o fórmula oracional .
Una fórmula proposicional se construye a partir de proposiciones simples , como "cinco es mayor que tres" o variables proposicionales como p y q , utilizando conectivos u operadores lógicos como NOT, AND, OR o IMPLIES; Por ejemplo:
En matemáticas , una fórmula proposicional a menudo se denomina más brevemente " proposición ", pero, más precisamente, una fórmula proposicional no es una proposición sino una expresión formal que denota una proposición , un objeto formal en discusión, al igual que una expresión como ya que " x + y " no es un valor, pero denota un valor. En algunos contextos, mantener la distinción puede ser importante.
A los efectos del cálculo proposicional, las proposiciones (enunciados, oraciones, afirmaciones) se consideran simples o compuestas. [1] Se considera que las proposiciones compuestas están unidas por conectivos oracionales, algunos de los más comunes son "Y", "O", "SI... ENTONCES...", "NI... NI... ", "... ES EQUIVALENTE A ..." . El punto y coma de enlace ";" y el conectivo "PERO" se consideran expresiones de "Y". Se considera que una secuencia de oraciones discretas está unida por "Y", y el análisis formal aplica una "regla de paréntesis" recursiva con respecto a secuencias de proposiciones simples (ver más abajo sobre fórmulas bien formadas).
Las proposiciones simples son de naturaleza declarativa, es decir, hacen afirmaciones sobre la condición o naturaleza de un objeto de sensación particular , por ejemplo, "Esta vaca es azul", "¡Hay un coyote!" ("Ese coyote ESTÁ ahí , detrás de las rocas"). [2] Así, las afirmaciones "primitivas" simples deben referirse a objetos específicos o estados mentales específicos. Cada uno debe tener al menos un sujeto (un objeto inmediato de pensamiento u observación), un verbo (preferiblemente en voz activa y tiempo presente) y tal vez un adjetivo o adverbio. "¡Perro!" probablemente implique "Veo un perro", pero debería rechazarse por ser demasiado ambiguo.
A los efectos del cálculo proposicional, una proposición compuesta normalmente puede reformularse en una serie de oraciones simples, aunque el resultado probablemente suene forzado.
El cálculo de predicados va un paso más allá que el cálculo proposicional hacia un "análisis de la estructura interna de las proposiciones" [3] Divide una oración simple en dos partes (i) su sujeto (el objeto ( singular o plural) del discurso) y (ii) un predicado (un verbo o posiblemente una cláusula verbal que afirma una cualidad o atributo del objeto(s)). El cálculo de predicados luego generaliza la forma "sujeto|predicado" (donde | simboliza la concatenación (encadenamiento) de símbolos) en una forma con la siguiente estructura de sujeto en blanco " ___|predicado", y el predicado a su vez se generaliza a todas las cosas con esa propiedad.
La generalización de "este cerdo" a un miembro (potencial) de dos clases "cosas aladas" y "cosas azules" significa que tiene una relación de verdad con ambas clases. En otras palabras, dado un dominio del discurso "cosas aladas", se considera que p es miembro de este dominio o no. Por lo tanto, existe una relación W (alado) entre p (cerdo) y { T, F }, W(p) se evalúa como { T, F } donde { T, F } es el conjunto de los valores booleanos "verdadero" y " FALSO". Lo mismo ocurre con B (azul) y p (cerdo) y { T, F }: B(p) se evalúa como { T, F }. Así que ahora podemos analizar las afirmaciones conectadas "B(p) Y W(p)" para determinar su valor de verdad general, es decir:
En particular, el cálculo de predicados trata las oraciones simples que emplean nociones de "todos", "algunos", "unos pocos", "uno de", etc., llamadas cuantificadores lógicos . Junto con el nuevo simbolismo de la función "F(x)" se introducen dos nuevos símbolos: ∀ (Para todos) y ∃ (Existe..., Existe al menos uno de..., etc.). El cálculo de predicados, pero no el cálculo proposicional, puede establecer la validez formal del siguiente enunciado:
Tarski afirma que la noción de IDENTIDAD (a diferencia de la EQUIVALENCIA LÓGICA) se encuentra fuera del cálculo proposicional; sin embargo, señala que si una lógica ha de ser útil para las matemáticas y las ciencias debe contener una "teoría" de la IDENTIDAD. [4] Algunos autores se refieren a "lógica de predicados con identidad" para enfatizar esta extensión. Vea más sobre esto a continuación.
Un álgebra (y hay muchos diferentes), definido de manera vaga, es un método mediante el cual se combina una colección de símbolos llamados variables junto con algunos otros símbolos como paréntesis (,) y algún subconjunto de símbolos como *, +, ~. , &, ∨, =, ≡, ∧, ¬ se manipulan dentro de un sistema de reglas. Se dice que estos símbolos, y sus cadenas bien formadas, representan objetos, pero en un sistema algebraico específico estos objetos no tienen significado. Así, el trabajo dentro del álgebra se convierte en un ejercicio de obediencia a ciertas leyes (reglas) de la sintaxis del álgebra (formación de símbolos) más que en la semántica (significado) de los símbolos. Los significados se encuentran fuera del álgebra.
Para que una secuencia bien formada de símbolos en el álgebra —una fórmula— tenga alguna utilidad fuera del álgebra, a los símbolos se les asignan significados y eventualmente a las variables se les asignan valores; luego mediante una serie de reglas se evalúa la fórmula.
Cuando los valores se restringen a sólo dos y se aplican a la noción de oraciones simples (por ejemplo, expresiones habladas o afirmaciones escritas) unidas por conectivos proposicionales, todo este sistema algebraico de símbolos, reglas y métodos de evaluación suele denominarse cálculo proposicional o cálculo oracional. .
Si bien algunas de las reglas familiares del álgebra aritmética continúan siendo válidas en el álgebra de proposiciones (por ejemplo, las leyes conmutativas y asociativas para AND y OR), otras no (por ejemplo, las leyes distributivas para AND, OR y NOT).
Análisis: En el razonamiento deductivo , los filósofos, retóricos y matemáticos reducen los argumentos a fórmulas y luego los estudian (generalmente con tablas de verdad ) para determinar su corrección (solidez). Por ejemplo: ¿Es sólido el siguiente argumento?
Los ingenieros analizan los circuitos lógicos que han diseñado utilizando técnicas de síntesis y luego aplican diversas técnicas de reducción y minimización para simplificar sus diseños.
Síntesis: los ingenieros en particular sintetizan fórmulas proposicionales (que eventualmente terminan como circuitos de símbolos) a partir de tablas de verdad . Por ejemplo, se podría escribir una tabla de verdad sobre cómo debería comportarse la suma binaria dada la suma de las variables "b" y "a" y "carry_in" "ci", y los resultados "carry_out" "co" y "sum" Σ :
El tipo más simple de fórmula proposicional es una variable proposicional . Las proposiciones que son simples ( atómicas ), las expresiones simbólicas a menudo se denotan mediante variables denominadas p , q , o P , Q , etc. Una variable proposicional pretende representar una proposición atómica (afirmación), como "Es sábado" = p (aquí el símbolo = significa "... se le asigna la variable nombrada...") o "Sólo voy al cine los lunes" = q .
La evaluación de una fórmula proposicional comienza con la asignación de un valor de verdad a cada variable. Debido a que cada variable representa una oración simple, los valores de verdad se aplican a la "verdad" o "falsedad" de estas oraciones simples.
Valores de verdad en retórica, filosofía y matemáticas.
Los valores de verdad son sólo dos: {VERDAD "T", FALSIDAD "F" }. Un empirista clasifica todas las proposiciones en dos grandes clases: analíticas —verdaderas pase lo que pase (por ejemplo, tautología ), y sintéticas —derivadas de la experiencia y, por tanto, susceptibles de confirmación por terceros (la teoría de la verificación del significado). [5] Los empiristas sostienen que, en general, para llegar al valor de verdad de una proposición sintética , primero se deben aplicar significados (plantillas de coincidencia de patrones) a las palabras, y luego estas plantillas de significado deben compararse con lo que sea que sea. eso se está afirmando. Por ejemplo, mi expresión "¡Esa vaca es azul !" ¿Es esta afirmación una VERDAD? En verdad lo dije. Y tal vez esté viendo una vaca azul; a menos que esté mintiendo, mi afirmación es una VERDAD en relación con el objeto de mi (quizás defectuosa) percepción. ¿Pero la vaca azul está "realmente ahí"? ¿Qué ves cuando miras por la misma ventana? Para proceder con una verificación, necesitará una noción previa (una plantilla) tanto de "vaca" como de " azul ", y la capacidad de hacer coincidir las plantillas con el objeto de sensación (si es que existe uno). [ cita necesaria ]
Valores de verdad en ingeniería.
Los ingenieros intentan evitar las nociones de verdad y falsedad que atormentan a los filósofos, pero en última instancia, los ingenieros deben confiar en sus instrumentos de medición. En su búsqueda de robustez , los ingenieros prefieren extraer objetos conocidos de una pequeña biblioteca: objetos que tienen comportamientos bien definidos y predecibles incluso en grandes combinaciones (de ahí el nombre del cálculo proposicional: "lógica combinatoria"). La menor cantidad de comportamientos de un solo objeto son dos (por ejemplo, {OFF, ON}, {abrir, cerrar}, {ARRIBA, ABAJO}, etc.), y estos se ponen en correspondencia con {0, 1}. Estos elementos se denominan digitales ; aquellos con una gama continua de comportamientos se denominan analógicos . Siempre que se deben tomar decisiones en un sistema analógico, muy a menudo un ingeniero convertirá un comportamiento analógico (la puerta está 45,32146% ARRIBA) a digital (por ejemplo, ABAJO=0) mediante el uso de un comparador . [6]
Así, una asignación de significado de las variables y de los dos símbolos de valor { 0, 1 } proviene "de fuera" de la fórmula que representa el comportamiento del objeto (normalmente) compuesto. Un ejemplo es una puerta de garaje con dos "interruptores de límite", uno para ARRIBA con la etiqueta SW_U y otro para ABAJO con la etiqueta SW_D, y cualquier otra cosa que esté en el circuito de la puerta. La inspección del circuito (ya sea el diagrama o los objetos reales: puerta, interruptores, cables, placa de circuito, etc.) puede revelar que, en la placa de circuito, el "nodo 22" llega a +0 voltios cuando los contactos del interruptor "SW_D " están mecánicamente en contacto ("cerrado") y la puerta está en la posición "abajo" (95% abajo), y el "nodo 29" pasa a +0 voltios cuando la puerta está 95% ARRIBA y los contactos del interruptor SW_U están en contacto mecánico ("cerrado"). [7] El ingeniero debe definir los significados de estos voltajes y todas las combinaciones posibles (las 4), incluidas las "malas" (por ejemplo, ambos nodos 22 y 29 a 0 voltios, lo que significa que la puerta está abierta y cerrada en el Mismo tiempo). El circuito responde sin pensar a cualquier voltaje que experimente sin ninguna conciencia de VERDAD o FALSEIDAD, CORRECTO o INCORRECTO, SEGURO o PELIGROSO. [ cita necesaria ]
Las fórmulas proposicionales arbitrarias se construyen a partir de variables proposicionales y otras fórmulas proposicionales que utilizan conectivos proposicionales . Ejemplos de conectivos incluyen:
Los siguientes son los conectivos comunes a la retórica, la filosofía y las matemáticas junto con sus tablas de verdad . Los símbolos utilizados variarán de un autor a otro y entre campos de actividad. En general, las abreviaturas "T" y "F" representan las evaluaciones VERDAD y FALSIDAD aplicadas a las variables en la fórmula proposicional (por ejemplo, la afirmación: "Esa vaca es azul" tendrá el valor de verdad "T" para Verdad o " F" de Falsedad, según sea el caso).
Los conectivos tienen distintos usos de palabras, por ejemplo, "a IMPLICA b" también se dice "SI a ENTONCES b". Algunos de estos se muestran en la tabla.
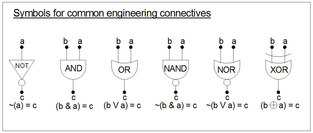
En general, los conectivos de ingeniería son iguales que los conectivos de matemáticas, excepto que tienden a evaluarse con "1" = "T" y "0" = "F". Esto se hace con el fin de analizar/minimizar y sintetizar fórmulas mediante el uso de la noción de mintérminos y mapas de Karnaugh (ver más abajo). Los ingenieros también utilizan las palabras producto lógico de la noción de Boole (a*a = a) y suma lógica de la noción de Jevons (a+a = a). [8]
El conectivo SI... ENTONCES... ELSE... aparece como la forma más simple de operador CASO de la teoría de la recursividad y la teoría de la computación y es el conectivo responsable de los goto condicionales (saltos, ramas). A partir de este conectivo se pueden construir todos los demás conectivos (ver más abajo). Aunque "IF c THEN b ELSE a" suena como una implicación, es, en su forma más reducida, un cambio que toma una decisión y ofrece como resultado sólo una de dos alternativas "a" o "b" (de ahí el nombre de declaración de cambio) . en el lenguaje de programación C ). [9]
Las siguientes tres proposiciones son equivalentes (como lo indica el signo de equivalencia lógica ≡):
Por lo tanto, SI... ENTONCES... ELSE—a diferencia de la implicación—no se evalúa como una "VERDAD" ambigua cuando la primera proposición es falsa, es decir, c = F en (c → b). Por ejemplo, la mayoría de la gente rechazaría la siguiente proposición compuesta como un non sequitur sin sentido porque la segunda oración no está conectada en significado con la primera. [10]
En reconocimiento de este problema, el signo → de la implicación formal en el cálculo proposicional se llama implicación material para distinguirla de la implicación intuitiva cotidiana. [a]
El uso de la construcción SI... ENTONCES... ELSE evita la controversia porque ofrece una elección completamente determinista entre dos alternativas declaradas; ofrece dos "objetos" (las dos alternativas b y a), y selecciona entre ellos de forma exhaustiva e inequívoca. [12] En la siguiente tabla de verdad, d1 es la fórmula: ((SI c ENTONCES b) Y (SI NO-c ENTONCES a)). Su forma completamente reducida d2 es la fórmula: ( (c Y b) O (NO-c Y a). Las dos fórmulas son equivalentes como lo muestran las columnas "=d1" y "=d2". Los ingenieros eléctricos llaman a la forma completamente reducida formula el operador AND-OR-SELECT. El operador CASE (o SWITCH) es una extensión de la misma idea a n resultados posibles, pero mutuamente excluyentes. Los ingenieros eléctricos llaman al operador CASE multiplexor .
La primera tabla de esta sección incluye *** la entrada equivalencia lógica para señalar el hecho de que " equivalencia lógica " no es lo mismo que "identidad". Por ejemplo, la mayoría estaría de acuerdo en que la afirmación "Esa vaca es azul" es idéntica a la afirmación "Esa vaca es azul". Por otro lado, a veces aparece equivalencia lógica en el habla, como en este ejemplo: "'El sol brilla' significa 'Estoy en bicicleta'". Traducidas a una fórmula proposicional, las palabras se convierten en: "SI 'el sol brilla' ENTONCES ' Estoy en bicicleta', Y SI 'estoy en bicicleta' ENTONCES 'el sol brilla'": [13]
Diferentes autores utilizan diferentes signos para la equivalencia lógica: ↔ (por ejemplo, Suppes, Goodstein, Hamilton), ≡ (por ejemplo, Robbin), ⇔ (por ejemplo, Bender y Williamson). Normalmente, la identidad se escribe como el signo igual =. Una excepción a esta regla se encuentra en Principia Mathematica . Para más información sobre la filosofía de la noción de IDENTIDAD, consulte la ley de Leibniz .
Como se señaló anteriormente, Tarski considera que la IDENTIDAD se encuentra fuera del cálculo proposicional, pero afirma que sin la noción, la "lógica" es insuficiente para las matemáticas y las ciencias deductivas. De hecho, el signo entra en el cálculo proposicional cuando se va a evaluar una fórmula. [14]
En algunos sistemas no hay tablas de verdad, sino simplemente axiomas formales (por ejemplo, cadenas de símbolos de un conjunto { ~, →, (,), variables p 1 , p 2 , p 3 , ... } y reglas de formación de fórmulas. (reglas sobre cómo hacer más cadenas de símbolos a partir de cadenas anteriores mediante el uso de, por ejemplo, sustitución y modus ponens ). El resultado de dicho cálculo será otra fórmula (es decir, una cadena de símbolos bien formada). Sin embargo, eventualmente, si uno quiere Para utilizar el cálculo para estudiar las nociones de validez y verdad, hay que agregar axiomas que definen el comportamiento de los símbolos llamados "los valores de verdad" {T, F} (o {1, 0}, etc.) con respecto a los demás símbolos.
Por ejemplo, Hamilton usa dos símbolos = y ≠ cuando define la noción de valoración v de cualquier fórmula bien formada (wffs) A y B en su "cálculo de enunciados formales" L. Una valoración v es una función de las wffs de su sistema L al rango (salida) { T, F }, dado que a cada variable p 1 , p 2 , p 3 en un wff se le asigna un valor de verdad arbitrario { T, F }.
Las dos definiciones ( i ) y ( ii ) definen el equivalente de las tablas de verdad para los conectivos ~ (NOT) y → (IMPLICACIÓN) de su sistema. Del primero se deriva F ≠ T y T ≠ F, es decir " v ( A ) no significa v (~ A )". La definición ( ii ) especifica la tercera fila de la tabla de verdad, y las otras tres filas provienen de una aplicación de la definición ( i ). En particular ( ii ) asigna el valor F (o un significado de "F") a la expresión completa. Las definiciones también sirven como reglas de formación que permiten la sustitución de un valor previamente derivado en una fórmula:
Algunos sistemas formales especifican estos axiomas de valoración desde el principio en forma de ciertas fórmulas como la ley de contradicción o las leyes de identidad y nulidad. La elección de cuáles usar, junto con leyes como las de conmutación y distribución, depende del diseñador del sistema siempre que el conjunto de axiomas esté completo (es decir, suficiente para formar y evaluar cualquier fórmula bien formada creada en el sistema). .
Como se muestra arriba, el conectivo CASO (SI c ENTONCES b ELSE a) se construye a partir de los conectivos de 2 argumentos SI... ENTONCES... y Y o de O y Y y el argumento NO. Los conectivos como el argumento n AND (a & b & c & ... & n), OR (a ∨ b ∨ c ∨ ... ∨ n) se construyen a partir de cadenas de dos argumentos AND y OR y se escriben en forma abreviada sin paréntesis. Estos, y también otros conectivos, pueden usarse como bloques de construcción para otros conectivos aún más. Los retóricos, filósofos y matemáticos utilizan tablas de verdad y diversos teoremas para analizar y simplificar sus fórmulas.
La ingeniería eléctrica utiliza símbolos dibujados y los conecta con líneas que representan el acto matemático de sustitución y reemplazo. Luego verifican sus dibujos con tablas de verdad y simplifican las expresiones como se muestra a continuación mediante el uso de mapas de Karnaugh o los teoremas. De esta manera, los ingenieros han creado una gran cantidad de "lógica combinatoria" (es decir, conectivos sin retroalimentación) como "decodificadores", "codificadores", "puertas multifunción", "lógica mayoritaria", "sumadores binarios", "unidades lógicas aritméticas", etc.
Una definición crea un nuevo símbolo y su comportamiento, a menudo con fines de abreviatura. Una vez presentada la definición, se puede utilizar cualquier forma del símbolo equivalente o fórmula. El siguiente simbolismo = Df sigue la convención de Reichenbach. [15] Algunos ejemplos de definiciones convenientes extraídas del conjunto de símbolos { ~, &, (, ) } y variables. Cada definición produce una fórmula lógicamente equivalente que puede usarse para sustitución o reemplazo.
Las definiciones anteriores para OR, IMPLICACIÓN, XOR y equivalencia lógica son en realidad esquemas (o "esquemas"), es decir, son modelos (demostraciones, ejemplos) para un formato de fórmula general pero que se muestran (con fines ilustrativos) con letras específicas a. , b, c para las variables, mientras que cualquier letra variable puede ir en su lugar siempre que las sustituciones de letras sigan la regla de sustitución siguiente.
Sustitución : La variable o subfórmula que se va a sustituir por otra variable, constante o subfórmula debe reemplazarse en todos los casos a lo largo de la fórmula general.
Reemplazo : (i) la fórmula a reemplazar debe estar dentro de una tautología, es decir, lógicamente equivalente (conectada por ≡ o ↔) a la fórmula que la reemplaza, y (ii) a diferencia de la sustitución, se permite que el reemplazo ocurra solo en un lugar (es decir, para una fórmula).
La presentación clásica de la lógica proposicional (ver Enderton 2002) utiliza los conectivos . El conjunto de fórmulas sobre un conjunto dado de variables proposicionales se define inductivamente como el conjunto más pequeño de expresiones tales que:
Esta definición inductiva se puede ampliar fácilmente para cubrir conectivos adicionales.
La definición inductiva también puede reformularse en términos de operación de cierre (Enderton 2002). Sea V un conjunto de variables proposicionales y X V el conjunto de todas las cadenas de un alfabeto, incluidos los símbolos en V , los paréntesis izquierdo y derecho y todos los conectivos lógicos considerados. Cada conectivo lógico corresponde a una operación de construcción de fórmulas, una función de XX V a XX V :
El conjunto de fórmulas sobre V se define como el subconjunto más pequeño de XX V que contiene V y está cerrado bajo todas las operaciones de construcción de fórmulas.
Las siguientes "leyes" del cálculo proposicional se utilizan para "reducir" fórmulas complejas. Las "leyes" se pueden verificar fácilmente con tablas de verdad. Para cada ley, el conectivo principal (más externo) está asociado con equivalencia lógica ≡ o identidad =. Un análisis completo de las 2 n combinaciones de valores de verdad para sus n variables distintas dará como resultado una columna de unos (T) debajo de este conectivo. Este hallazgo convierte a cada ley, por definición, en una tautología. Y, para una ley dada, debido a que sus fórmulas a la izquierda y a la derecha son equivalentes (o idénticas), pueden sustituirse entre sí.
Los lectores emprendedores podrían desafiarse a sí mismos a inventar un "sistema axiomático" que utilice los símbolos { ∨, &, ~, (, ), variables a, b, c }, las reglas de formación especificadas anteriormente y la menor cantidad posible de leyes enumeradas. a continuación, y luego derivar como teoremas los demás, así como las valoraciones de la tabla de verdad para ∨, & y ~. Un conjunto atribuido a Huntington (1904) (Suppes:204) utiliza ocho de las leyes definidas a continuación.
Si se usan en un sistema axiomático, los símbolos 1 y 0 (o T y F) se consideran fórmulas bien formadas y, por lo tanto, obedecen las mismas reglas que las variables. Por tanto, las leyes que se enumeran a continuación son en realidad esquemas axiomáticos , es decir, sustituyen a un número infinito de casos. Por lo tanto, ( x ∨ y ) ≡ ( y ∨ x ) podría usarse en un caso, ( p ∨ 0 ) ≡ ( 0 ∨ p ) y en otro caso ( 1 ∨ q ) ≡ ( q ∨ 1 ), etc.
En general, para evitar confusión durante el análisis y evaluación de fórmulas proposicionales, se puede hacer un uso liberal de los paréntesis. Sin embargo, muy a menudo los autores los omiten. Para analizar una fórmula complicada, primero es necesario conocer la antigüedad o rango que tiene cada uno de los conectivos (excepto *) sobre los demás. Para "formar bien" una fórmula, comience con el conectivo con el rango más alto y agregue paréntesis alrededor de sus componentes, luego baje de rango (prestando mucha atención al alcance del conectivo sobre el cual está trabajando). De mayor a menor rango, con los signos de predicado ∀x y ∃x, IDENTIDAD = y signos aritméticos agregados para completar: [b]
Por lo tanto, la fórmula se puede analizar, pero como NOT no obedece la ley distributiva, el paréntesis alrededor de la fórmula interna (~c & ~d) es obligatorio:
Tanto AND como OR obedecen la ley conmutativa y la ley asociativa :
Omitir paréntesis en cadenas de AND y OR : las conectivas se consideran unarias (de una variable, por ejemplo, NOT) y binarias (es decir, AND, OR, DE dos variables, IMPLICA). Por ejemplo:
Sin embargo, una demostración con una tabla de verdad muestra que la forma sin paréntesis adicionales es perfectamente adecuada.
Omitir paréntesis con respecto a una variable única NOT : Si bien ~(a) donde a es una variable única está perfectamente claro, ~a es adecuado y es la forma habitual en que aparecería este literal . Cuando el NOT está sobre una fórmula con más de un símbolo, entonces los paréntesis son obligatorios, por ejemplo ~(a ∨ b).
OR distribuye sobre AND y AND distribuye sobre OR. NOT no se distribuye sobre AND u OR. Vea a continuación sobre la ley de De Morgan:
NOT, cuando se distribuye sobre OR o AND, hace algo peculiar (nuevamente, esto se puede verificar con una tabla de verdad):
La absorción, en particular la primera, hace que las "leyes" de la lógica difieran de las "leyes" de la aritmética:
El signo " = " (a diferencia de la equivalencia lógica ≡, alternativamente ↔ o ⇔) simboliza la asignación de valor o significado. Por lo tanto, la cadena (a & ~(a)) simboliza "0", es decir, significa lo mismo que el símbolo "0" ". En algunos "sistemas" esto será un axioma (definición) que tal vez se muestre como ( (a & ~ (a)) = Df 0); en otros sistemas, se puede derivar de la siguiente tabla de verdad:
Una propiedad clave de las fórmulas es que pueden analizarse de forma única para determinar la estructura de la fórmula en términos de sus variables proposicionales y conectivos lógicos. Cuando las fórmulas se escriben en notación infija , como se indicó anteriormente, se garantiza una legibilidad única mediante el uso apropiado de paréntesis en la definición de las fórmulas. Alternativamente, las fórmulas se pueden escribir en notación polaca o en notación polaca inversa , eliminando por completo la necesidad de paréntesis.
La definición inductiva de fórmulas infijas de la sección anterior se puede convertir a una gramática formal en la forma Backus-Naur :
< fórmula > ::= < variable proposicional >
| ( ¬ < fórmula > )| ( < fórmula > ∧ < fórmula > )| ( < fórmula > ∨ < fórmula > )| ( < fórmula > → < fórmula > )| ( < fórmula > ↔ < fórmula > )Se puede demostrar que cualquier expresión que coincida con la gramática tiene un número equilibrado de paréntesis izquierdo y derecho, y cualquier segmento inicial no vacío de una fórmula tiene más paréntesis izquierdo que derecho. [17] Este hecho se puede utilizar para proporcionar un algoritmo para analizar fórmulas. Por ejemplo, supongamos que una expresión x comienza con . Comenzando después del segundo símbolo, haga coincidir la subexpresión y más corta de x que tenga paréntesis equilibrados. Si x es una fórmula, queda exactamente un símbolo después de esta expresión, este símbolo es un paréntesis de cierre e y en sí es una fórmula. Esta idea se puede utilizar para generar un analizador de descenso recursivo para fórmulas.
Ejemplo de conteo entre paréntesis :
Este método ubica como "1" el conectivo principal , el conectivo bajo el cual ocurre la evaluación general de la fórmula para los paréntesis más externos (que a menudo se omiten). [18] También localiza el conectivo más interno donde se comenzaría la evaluación de la fórmula sin el uso de una tabla de verdad, por ejemplo en el "nivel 6".
La noción de argumento válido generalmente se aplica a inferencias en argumentos, pero los argumentos se reducen a fórmulas proposicionales y pueden evaluarse de la misma manera que cualquier otra fórmula proposicional. Aquí una inferencia válida significa: "La fórmula que representa la inferencia se evalúa como "verdad" debajo de su conectivo principal, sin importar qué valores de verdad se asignen a sus variables", es decir, la fórmula es una tautología. [19] Es muy posible que una fórmula esté bien formada pero no sea válida. Otra forma de decir esto es: “Estar bien formado es necesario para que una fórmula sea válida pero no es suficiente ”. La única manera de saber si está bien formado y es válido es someterlo a verificación con una tabla de verdad o mediante el uso de las "leyes":

Un conjunto de conectivos lógicos se llama completo si cada fórmula proposicional es tautológicamente equivalente a una fórmula con solo los conectivos de ese conjunto. Hay muchos conjuntos completos de conectivos, incluidos , y . Hay dos conectivos binarios que son completos por sí solos, correspondientes a NAND y NOR, respectivamente. [20] Algunos pares no están completos, por ejemplo .
El conectivo binario correspondiente a NAND se llama trazo de Sheffer y se escribe con una barra vertical | o flecha vertical ↑. La integridad de este conectivo se observó en Principia Mathematica (1927: xvii). Dado que es completo por sí solo, todos los demás conectivos se pueden expresar utilizando únicamente el trazo. Por ejemplo, donde el símbolo " ≡ " representa equivalencia lógica :
En particular, los conectivos cero-arios (que representan la verdad) y (que representan la falsedad) se pueden expresar usando el trazo:
Este conectivo junto con { 0, 1 }, (o { F, T } o { , } ) forma un conjunto completo. A continuación, la relación SI...ENTONCES...ELSE (c, b, a) = d representa ( (c → b) ∨ (~c → a) ) ≡ ( (c & b) ∨ (~c & a) ) = d
Ejemplo: A continuación se muestra cómo procedería una prueba basada en teoremas de "(c, b, 1) ≡ (c → b)", debajo de la prueba está su verificación de la tabla de verdad. (Nota: (c → b) se define como (~c ∨ b) ):
En la siguiente tabla de verdad, la columna denominada "tensa" para tautología evalúa la equivalencia lógica (simbolizada aquí por ≡) entre las dos columnas denominadas d. Debido a que las cuatro filas debajo de "tenso" son unos, la equivalencia de hecho representa una tautología.
Una fórmula proposicional arbitraria puede tener una estructura muy complicada. A menudo resulta conveniente trabajar con fórmulas que tienen formas más simples, conocidas como formas normales . Algunas formas normales comunes incluyen la forma normal conjuntiva y la forma normal disyuntiva . Cualquier fórmula proposicional puede reducirse a su forma normal conjuntiva o disyuntiva.

La reducción a la forma normal es relativamente sencilla una vez que se prepara una tabla de verdad para la fórmula. Pero nuevos intentos de minimizar el número de literales (ver más abajo) requieren algunas herramientas: la reducción mediante las leyes de De Morgan y las tablas de verdad puede ser difícil de manejar, pero los mapas de Karnaugh son muy adecuados para un número pequeño de variables (5 o menos). Existen algunos métodos tabulares sofisticados para circuitos más complejos con múltiples salidas, pero están fuera del alcance de este artículo; Para obtener más información, consulte Algoritmo de Quine-McCluskey .
En ingeniería eléctrica, una variable x o su negación ~(x) puede denominarse literal . Una cadena de literales conectados mediante AND se denomina término. Una cadena de literales conectados por OR se llama alterm. Normalmente, el literal ~(x) se abrevia ~x. A veces, el símbolo & se omite por completo en la forma de multiplicación algebraica.
De la misma manera que una tabla de verdad de 2 n filas muestra la evaluación de una fórmula proposicional para los 2 n valores posibles de sus variables, n variables produce un mapa de Karnaugh de 2 n cuadrados (aunque no podemos dibujarlo en su totalidad). realización dimensional). Por ejemplo, 3 variables producen 2 3 = 8 filas y 8 cuadrados de Karnaugh; 4 variables producen 16 filas de la tabla de verdad y 16 cuadrados y, por lo tanto, 16 mintérminos . Cada cuadrado del mapa de Karnaugh y su correspondiente evaluación de la tabla de verdad representan un minitérmino.
Cualquier fórmula proposicional puede reducirse a la "suma lógica" (OR) de los mintérminos activos (es decir, con valor "1" o "T"). Cuando está en esta forma se dice que la fórmula está en forma normal disyuntiva . Pero aunque tenga esta forma, no necesariamente se minimiza con respecto al número de términos ni al número de literales.
En la siguiente tabla observa la peculiar numeración de las filas: (0, 1, 3, 2, 6, 7, 5, 4, 0). La primera columna es el equivalente decimal del equivalente binario de los dígitos "cba", es decir:
Esta numeración se produce porque a medida que uno avanza en la tabla de una fila a otra, solo una variable a la vez cambia su valor. El código Gray se deriva de esta noción. Esta noción se puede extender a hipercubos de tres y cuatro dimensiones llamados diagramas de Hasse , donde las variables de cada esquina cambian solo una a la vez a medida que uno se mueve alrededor de los bordes del cubo. Los diagramas de Hasse (hipercubos) aplanados en dos dimensiones son diagramas de Veitch o mapas de Karnaugh (son prácticamente lo mismo).
Cuando se trabaja con mapas de Karnaugh, siempre se debe tener en cuenta que el borde superior "se envuelve" hasta el borde inferior, y el borde izquierdo se envuelve hasta el borde derecho; el diagrama de Karnaugh es en realidad un diagrama de tres, cuatro o n dimensiones. objeto aplanado.
Veitch mejoró la noción de diagramas de Venn al convertir los círculos en cuadrados contiguos, y Karnaugh simplificó el diagrama de Veitch al convertir los minitérminos, escritos en su forma literal (por ejemplo, ~abc~d) en números. [21] El método procede de la siguiente manera:
Elabora la tabla de verdad de la fórmula. Numere sus filas usando los equivalentes binarios de las variables (generalmente solo secuencialmente de 0 a n-1) para n variables.
Ejemplo: ((c & d) ∨ (p & ~(c & (~d)))) = q en forma normal conjuntiva es:
Sin embargo, esta fórmula se reducirá tanto en el número de términos (de 4 a 3) como en el cómputo total de sus literales (12 a 6).

Utilice los valores de la fórmula (por ejemplo, "p") encontrados mediante el método de la tabla de verdad y colóquelos en sus respectivos cuadrados de Karnaugh (asociados) (éstos están numerados según la convención del código Gray). Si en la tabla aparecen valores de "d" para "no me importa", esto añade flexibilidad durante la fase de reducción.
Los minitérminos de 1 cuadrados adyacentes (contiguos) (cuadrados T) se pueden reducir con respecto al número de sus literales , y los términos numéricos también se reducirán en el proceso. Dos cuadrados contiguos (2 x 1 horizontal o 1 x 2 vertical, incluso los bordes representan cuadrados contiguos) pierden un literal, cuatro cuadrados en un rectángulo de 4 x 1 (horizontal o vertical) o un cuadrado de 2 x 2 (incluso las cuatro esquinas representan cuadrados) pierden dos literales, ocho cuadrados en un rectángulo pierden 3 literales, etc. (Se busca el cuadrado o rectángulos más grande e ignora los cuadrados o rectángulos más pequeños contenidos totalmente en él). Este proceso continúa hasta que se contabilizan todos los cuadrados contiguos, momento en el que se minimiza la fórmula proposicional.
Por ejemplo, los cuadrados 3 y 7 colindan. Estos dos cuadrados contiguos pueden perder un literal (por ejemplo, "p" de los cuadrados #3 y #7), cuatro cuadrados en un rectángulo o cuadrado pierden dos literales, ocho cuadrados en un rectángulo pierden 3 literales, etc. (Se busca el más grande cuadrado o rectángulos.) Este proceso continúa hasta que se tienen en cuenta todos los cuadrados contiguos, momento en el que se dice que la fórmula proposicional está minimizada.
Ejemplo: el método del mapa generalmente se realiza mediante inspección. El siguiente ejemplo amplía el método algebraico para mostrar el "truco" detrás de la combinación de términos en un mapa de Karnaugh:
Observe que por la ley de Idempotencia (A ∨ A) = A, podemos crear más términos. Luego, mediante leyes de asociación y distributivas, las variables que desaparecerán se pueden emparejar y luego "desaparecer" con la Ley de contradicción (x & ~x)=0. A continuación se utilizan corchetes [y] sólo para realizar un seguimiento de los términos; no tienen ningún significado especial:
Dados los siguientes ejemplos-como-definiciones, ¿qué se hace con el razonamiento siguiente?
Luego asigne la variable "s" a la oración más a la izquierda "Esta oración es simple". Defina "compuesto" c = "no simple" ~s y asigne c = ~s a "Esta oración es compuesta"; asigne "j" a "Esta oración está unida por AND". La segunda oración se puede expresar como:
Si se van a colocar valores de verdad en las oraciones c = ~s y j, entonces todas son claramente FALSEDADES: por ejemplo, "Esta oración es compleja" es una FALSA (es simple , por definición). Entonces su conjunción (Y) es una falsedad. Pero cuando se toma en su forma ensamblada, la oración es una VERDAD.
Este es un ejemplo de las paradojas que resultan de una definición impredicativa , es decir, cuando un objeto m tiene una propiedad P, pero el objeto m se define en términos de la propiedad P. [22] El mejor consejo para un retórico o alguien involucrado En el análisis deductivo se trata de evitar definiciones impredicativas pero al mismo tiempo estar atento a ellas porque de hecho pueden crear paradojas. Los ingenieros, en cambio, las ponen en práctica en forma de fórmulas proposicionales con retroalimentación.
La noción de una fórmula proposicional que aparece como una de sus propias variables requiere una regla de formación que permita la asignación de la fórmula a una variable. En general, no existe ninguna estipulación (ya sea sistemas de objetos y relaciones axiomáticos o de tablas de verdad) que prohíba que esto suceda. [23]
El caso más simple ocurre cuando una fórmula OR se convierte en una de sus propias entradas, por ejemplo, p = q. Comience con (p ∨ s) = q, luego sea p = q. Observe que la "definición" de q depende de sí mismo "q" así como de "s" y del conectivo OR; esta definición de q es, por tanto, impredicativa. Puede resultar cualquiera de dos condiciones: [24] oscilación o memoria.
Es útil pensar en la fórmula como una caja negra . Sin conocimiento de lo que sucede "dentro" de la "caja" de fórmulas desde el exterior, parecería que la salida ya no es función únicamente de las entradas. Es decir, a veces uno mira q y ve 0 y otras veces 1. Para evitar este problema hay que conocer el estado (condición) de la variable "oculta" p dentro del cuadro (es decir, el valor de q realimentado y asignado a pag). Cuando se sabe esto, la aparente inconsistencia desaparece.
Para comprender [predecir] el comportamiento de las fórmulas con retroalimentación se requiere un análisis más sofisticado de los circuitos secuenciales . Las fórmulas proposicionales con retroalimentación conducen, en su forma más simple, a máquinas de estados; también conducen a recuerdos en forma de cintas de Turing y contadores de contramáquinas. A partir de combinaciones de estos elementos se puede construir cualquier tipo de modelo computacional acotado (por ejemplo, máquinas de Turing , máquinas de contador , máquinas de registro , computadoras Macintosh , etc.).
En el caso abstracto (ideal), la fórmula oscilante más simple es NO retroalimentada a sí misma: ~(~(p=q)) = q. El análisis de una fórmula proposicional abstracta (ideal) en una tabla de verdad revela una inconsistencia tanto para los casos p=1 como para p=0: cuando p=1, q=0, esto no puede ser porque p=q; Lo mismo ocurre cuando p=0 y q=1.

Oscilación con retraso : si se inserta un retraso [25] (ideal o no ideal) en la fórmula abstracta entre p y q, entonces p oscilará entre 1 y 0: 101010...101... ad infinitum . Si cualquiera de los retardos y NOT no son abstractos (es decir, no son ideales), el tipo de análisis a utilizar dependerá de la naturaleza exacta de los objetos que componen el oscilador; cosas así quedan fuera de las matemáticas y dentro de la ingeniería.
El análisis requiere que se inserte un retraso y luego se corte el bucle entre el retraso y la entrada "p". El retraso debe verse como un tipo de proposición que tiene "qd" (q-retrasado) como salida y "q" como entrada. Esta nueva proposición añade otra columna a la tabla de verdad. La inconsistencia ahora está entre "qd" y "p", como se muestra en rojo; dos estados estables resultantes:

Sin demora, deben eliminarse las inconsistencias de un análisis de tabla de verdad. Con la noción de "retraso", esta condición se presenta como una inconsistencia momentánea entre la variable de salida retroalimentada q y p = q retrasado .
Una tabla de verdad revela las filas donde ocurren inconsistencias entre p = q retrasado en la entrada y q en la salida. Después de "romper" la retroalimentación, [26] la construcción de la tabla de verdad continúa de la manera convencional. Pero después, en cada fila la salida q se compara con la entrada p, ahora independiente, y se observa cualquier inconsistencia entre p y q (es decir, p=0 junto con q=1, o p=1 y q=0); cuando la "línea" se "rehace", ambas se vuelven imposibles por la Ley de contradicción ~(p & ~p)). Las filas que revelan inconsistencias se consideran estados transitorios o simplemente se eliminan como inconsistentes y, por lo tanto, "imposibles".
Acerca de la memoria más simple resulta cuando la salida de un OR se retroalimenta a una de sus entradas, en este caso la salida "q" se retroalimenta a "p". Dado que la fórmula se evalúa (inicializa) primero con p=0 y q=0, se "volteará" una vez cuando se "establezca" en s=1. A partir de entonces, la salida "q" mantendrá "q" en la condición "invertida" (estado q=1). Este comportamiento, ahora dependiente del tiempo, se muestra en el diagrama de estado a la derecha del cambio único.
El siguiente caso más simple es el flip-flop "set-reset" que se muestra debajo del flip-flop una vez. Dado que r=0 & s=0 y q=0 al principio, se "establece" (s=1) de una manera similar al cambio único. Sin embargo, tiene una disposición para "restablecer" q=0 cuando "r"=1. Y se produce una complicación adicional si tanto set=1 como reset=1. En esta fórmula, set=1 fuerza la salida q=1, de modo que cuando y si (s=0 y r=1), el flip-flop se reinicie. O, si (s=1 & r=0), se configurará el flip-flop. En el caso abstracto (ideal) en el que s=1 ⇒ s=0 y r=1 ⇒ r=0 simultáneamente, la fórmula q será indeterminada (indecidible). Debido a retrasos en el OR, el Y y el NO "reales", el resultado será desconocido al principio, pero a partir de entonces será predecible.
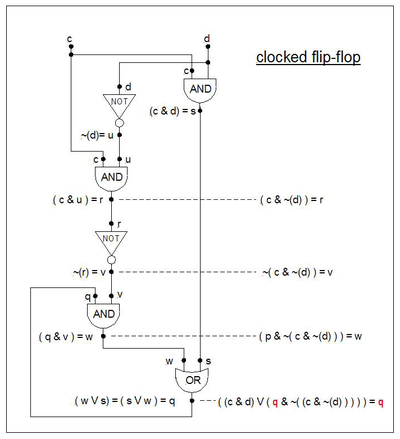
A continuación se proporciona la fórmula conocida como memoria " flip-flop sincronizada " ("c" es el "reloj" y "d" son los "datos"). Funciona de la siguiente manera: cuando c = 0, los datos d (ya sea 0 o 1) no pueden "transmitirse" para afectar la salida q. Cuando c = 1, los datos d "pasan" y la salida q "sigue" el valor de d. Cuando c pasa de 1 a 0, el último valor de los datos permanece "atrapado" en la salida "q". Siempre que c = 0, d puede cambiar de valor sin provocar que q cambie.
El diagrama de estado tiene una forma similar al diagrama de estado del flip-flop, pero con etiquetas diferentes en las transiciones.
Bertrand Russell (1912:74) enumera tres leyes de pensamiento que se derivan de Aristóteles : (1) La ley de identidad : "Todo lo que es, es", (2) La ley de no contradicción : "Nada puede ser y no ser al mismo tiempo". y (3) La ley del tercero excluido : "Todo debe ser o no ser".
El uso de la palabra "todo" en la ley del tercero excluido deja abierta al debate la expresión que hace Russell de esta ley. Si se restringe a una expresión sobre el SER o la CALIDAD con referencia a una colección finita de objetos (un "universo de discurso" finito) -cuyos miembros pueden ser investigados uno tras otro por la presencia o ausencia de la afirmación- entonces la ley se considera intuicionistamente apropiado. Por lo tanto, una afirmación como: "Este objeto debe SER o NO SER (en la colección)", o "Este objeto debe tener esta CALIDAD o NO tener esta CALIDAD (en relación con los objetos de la colección)" es aceptable. Ver más en el diagrama de Venn .
Aunque el cálculo proposicional se originó con Aristóteles, la noción de álgebra aplicada a proposiciones tuvo que esperar hasta principios del siglo XIX. En una reacción (adversa) a la tradición de 2000 años de silogismos de Aristóteles , el Ensayo sobre la comprensión humana (1690) de John Locke utilizó la palabra semiótica (teoría del uso de símbolos). En 1826 , Richard Whately había analizado críticamente la lógica silogística con simpatía hacia la semiótica de Locke. El trabajo de George Bentham (1827) dio como resultado la noción de "cuantificación del predicado" (1827) (hoy simbolizado como ∀ ≡ "para todos"). Una "disputa" instigada por William Hamilton sobre una disputa de prioridad con Augustus De Morgan "inspiró a George Boole a escribir sus ideas sobre lógica y publicarlas como MAL [Análisis matemático de la lógica] en 1847" (Grattin-Guinness y Bornet 1997). :xxviii).
Sobre su aportación Grattin-Guinness y Bornet comentan:
La enorme empresa de Gottlob Frege (1879) dio como resultado un cálculo formal de proposiciones, pero su simbolismo es tan desalentador que tuvo poca influencia excepto en una persona: Bertrand Russell . Primero, como alumno de Alfred North Whitehead, estudió la obra de Frege y sugirió una (famosa y notoria) enmienda con respecto a ella (1904) en torno al problema de una antinomia que descubrió en el tratamiento de Frege (cf. la paradoja de Russell ). El trabajo de Russell dio lugar a una colaboración con Whitehead que, en el año 1912, produjo el primer volumen de Principia Mathematica (PM). Es aquí donde apareció por primera vez lo que consideramos lógica proposicional "moderna". En particular, PM introduce NOT y OR y el símbolo de afirmación ⊦ como primitivas. En términos de estas nociones, definen IMPLICACIÓN → ( def. *1.01: ~p ∨ q ), luego Y (def. *3.01: ~(~p ∨ ~q) ), luego EQUIVALENCIA p ←→ q (*4.01: ( p → q) & ( q → p ) ).
Lógica de cálculo y conmutación :