

La resta (que se representa con el signo menos − ) es una de las cuatro operaciones aritméticas junto con la suma , la multiplicación y la división . La resta es una operación que representa la eliminación de objetos de una colección. [1] Por ejemplo, en la imagen adyacente, hay 5 − 2 duraznos, es decir, 5 duraznos a los que se les quitaron 2, lo que da un total de 3 duraznos. Por lo tanto, la diferencia de 5 y 2 es 3; es decir, 5 − 2 = 3 . Si bien se asocia principalmente con los números naturales en aritmética , la resta también puede representar la eliminación o disminución de cantidades físicas y abstractas utilizando diferentes tipos de objetos, incluidos números negativos , fracciones , números irracionales , vectores , decimales, funciones y matrices. [2]
En cierto sentido, la resta es la inversa de la suma. Es decir, c = a − b si y solo si c + b = a . En palabras: la diferencia de dos números es el número que da el primero al sumarlo al segundo.
La resta sigue varios patrones importantes. Es anticonmutativa , lo que significa que al cambiar el orden se cambia el signo del resultado. Tampoco es asociativa , lo que significa que cuando se restan más de dos números, el orden en el que se realiza la resta es importante. Como es la identidad aditiva , restarlo no cambia el número. La resta también obedece a reglas predecibles sobre operaciones relacionadas, como la suma y la multiplicación . Todas estas reglas se pueden demostrar , comenzando con la resta de números enteros y generalizando hasta los números reales y más allá. Las operaciones binarias generales que siguen estos patrones se estudian en álgebra abstracta .
En la teoría de la computabilidad , considerando que la resta no está bien definida sobre números naturales , las operaciones entre números en realidad se definen utilizando "resta truncada" o monus . [3]

La resta se escribe generalmente utilizando el signo menos "−" entre los términos; es decir, en notación infija . El resultado se expresa con un signo igual . Por ejemplo,
También hay situaciones en las que se "entiende" la resta, aunque no aparezca ningún símbolo: [ cita requerida ]
Formalmente, el número que se resta se conoce como sustraendo , [4] [5] mientras que el número del que se resta es el minuendo . [4] [5] El resultado es la diferencia . [4] [5] [2] [6] Es decir,
Toda esta terminología deriva del latín . "Substracción" es una palabra inglesa derivada del verbo latino subtrahere , que a su vez es un compuesto de sub "de debajo" y trahere "tirar". Por lo tanto, sustraer es sacar desde abajo , o quitar . [7] El uso del sufijo gerundivo -nd da como resultado "subtraendo", "cosa que se ha de sustraer". [a] Del mismo modo, de minuere "reducir o disminuir", se obtiene "minuendo", que significa "cosa que se ha de disminuir".
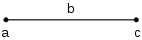
Imaginemos un segmento de línea de longitud b con el extremo izquierdo etiquetado como a y el extremo derecho etiquetado como c . Partiendo de a , se necesitan b pasos hacia la derecha para llegar a c . Este movimiento hacia la derecha se modela matemáticamente mediante la suma :
Desde c , se dan b pasos hacia la izquierda para volver a a . Este movimiento hacia la izquierda se modela mediante la resta:

Ahora, un segmento de línea etiquetado con los números 1 , 2 y 3. Desde la posición 3, no se necesitan pasos hacia la izquierda para permanecer en 3, por lo que 3 − 0 = 3. Se necesitan 2 pasos hacia la izquierda para llegar a la posición 1, por lo que 3 − 2 = 1. Esta imagen es inadecuada para describir lo que sucedería después de dar 3 pasos hacia la izquierda de la posición 3. Para representar tal operación, la línea debe extenderse.
Para restar números naturales arbitrarios , se comienza con una línea que contiene todos los números naturales (0, 1, 2, 3, 4, 5, 6, ...). Desde 3, se dan 3 pasos hacia la izquierda para llegar a 0, por lo que 3 − 3 = 0. Pero 3 − 4 sigue siendo inválido, ya que nuevamente sale de la línea. Los números naturales no son un contexto útil para la resta.
La solución es considerar la recta de números enteros (..., −3, −2, −1, 0, 1, 2, 3, ...). De esta manera, se dan 4 pasos hacia la izquierda desde 3 para llegar a −1:
La resta de números naturales no es cerrada : la diferencia no es un número natural a menos que el minuendo sea mayor o igual que el sustraendo. Por ejemplo, no se puede restar 26 de 11 para obtener un número natural. En este caso se utiliza uno de dos enfoques:
El campo de los números reales puede definirse especificando sólo dos operaciones binarias, la suma y la multiplicación, junto con operaciones unarias que dan lugar a inversos aditivos y multiplicativos . La resta de un número real (el sustraendo) de otro (el minuendo) puede definirse entonces como la suma del minuendo y el inverso aditivo del sustraendo. Por ejemplo, 3 − π = 3 + (− π ) . Alternativamente, en lugar de requerir estas operaciones unarias, las operaciones binarias de resta y división pueden tomarse como básicas.
La resta es anticonmutativa , lo que significa que si se invierten los términos de una diferencia de izquierda a derecha, el resultado es el negativo del resultado original. Simbólicamente, si a y b son dos números cualesquiera, entonces
La resta no es asociativa , lo que surge cuando se intenta definir la resta repetida. En general, la expresión
puede definirse como ( a − b ) − c o a − ( b − c ), pero estas dos posibilidades conducen a respuestas diferentes. Para resolver este problema, se debe establecer un orden de operaciones , en el que órdenes diferentes producen resultados diferentes.
En el contexto de los números enteros, la resta de uno también juega un papel especial: para cualquier número entero a , el número entero ( a − 1) es el mayor número entero menor que a , también conocido como el predecesor de a .
Al restar dos números con unidades de medida como kilogramos o libras , deben tener la misma unidad. En la mayoría de los casos, la diferencia tendrá la misma unidad que los números originales.
Los cambios en porcentajes se pueden informar en al menos dos formas: cambio porcentual y cambio porcentual en puntos . El cambio porcentual representa el cambio relativo entre las dos cantidades como porcentaje, mientras que el cambio porcentual en puntos es simplemente el número obtenido al restar los dos porcentajes. [8] [9] [10]
Por ejemplo, supongamos que el 30 % de los aparatos fabricados en una fábrica son defectuosos. Seis meses después, el 20 % de los aparatos son defectuosos. El cambio porcentual es 20% - 30%/30% = − 1/3 = −33+1/3 %, mientras que el cambio en puntos porcentuales es de -10 puntos porcentuales.
El método de complementos es una técnica que se utiliza para restar un número de otro utilizando únicamente la suma de números positivos. Este método se utilizaba comúnmente en calculadoras mecánicas y todavía se utiliza en computadoras modernas .
Para restar un número binario y (el sustraendo) de otro número x (el minuendo), se suma el complemento a uno de y a x y se suma uno a la suma. Luego se descarta el dígito inicial "1" del resultado.
El método de los complementos es especialmente útil en binario (base 2) ya que el complemento a uno se obtiene muy fácilmente invirtiendo cada bit (cambiando "0" por "1" y viceversa). Y la adición de 1 para obtener el complemento a dos se puede realizar simulando un acarreo en el bit menos significativo. Por ejemplo:
01100100 (x, es igual al decimal 100)- 00010110 (y, igual al decimal 22)
se convierte en la suma:
01100100 (x)+ 11101001 (complemento a uno de y)+ 1 (para obtener el complemento a dos)—————————— 101001110
Si eliminamos el "1" inicial, obtenemos la respuesta: 01001110 (equivale al decimal 78)
Los métodos que se utilizan para enseñar la resta en la escuela primaria varían de un país a otro y, dentro de un mismo país, se adoptan distintos métodos en diferentes momentos. En lo que se conoce en Estados Unidos como matemáticas tradicionales , se enseña a los estudiantes un proceso específico al final del primer año (o durante el segundo año) para utilizarlo con números enteros de varios dígitos, y se amplía en el cuarto o quinto grado para incluir representaciones decimales de números fraccionarios.
Casi todas las escuelas estadounidenses enseñan actualmente un método de resta que utiliza préstamos o reagrupación (el algoritmo de descomposición) y un sistema de marcas llamadas muletas. [11] [12] Aunque ya se conocía y se había publicado en libros de texto un método de préstamos, el uso de muletas en las escuelas estadounidenses se extendió después de que William A. Brownell publicara un estudio en el que afirmaba que las muletas eran beneficiosas para los estudiantes que usaban este método. [13] Este sistema se popularizó rápidamente y desplazó a los otros métodos de resta que se usaban en Estados Unidos en ese momento.
Algunas escuelas europeas emplean un método de resta llamado método austríaco, también conocido como método de adición. En este método no se toman prestadas las cantidades. También existen muletas (marcas para ayudar a la memoria), que varían según el país. [14] [15]
Ambos métodos dividen la resta en un proceso de restas de un dígito por valor posicional. Comenzando con el dígito menos significativo, se realiza una resta del sustraendo:
Desde el minuendo
donde cada s i y m i es un dígito, se procede escribiendo m 1 − s 1 , m 2 − s 2 , y así sucesivamente, siempre que s i no exceda a m i . De lo contrario, m i se incrementa en 10 y se modifica algún otro dígito para corregir este aumento. El método americano corrige intentando disminuir el dígito minuendo m i +1 en uno (o continuando el préstamo hacia la izquierda hasta que haya un dígito distinto de cero del cual tomar prestado). El método europeo corrige aumentando el dígito sustraendo s i +1 en uno.
Ejemplo: 704 − 512.
El minuendo es 704, el sustraendo es 512. Los dígitos del minuendo son m 3 = 7 , m 2 = 0 y m 1 = 4 . Los dígitos del sustraendo son s 3 = 5 , s 2 = 1 y s 1 = 2 . Comenzando en el lugar de las unidades, 4 no es menor que 2, por lo que la diferencia 2 se escribe en el lugar de las unidades del resultado. En el lugar de las decenas, 0 es menor que 1, por lo que el 0 se incrementa en 10, y la diferencia con 1, que es 9, se escribe en el lugar de las decenas. El método americano corrige el aumento de diez reduciendo el dígito en el lugar de las centenas del minuendo en uno. Es decir, se tacha el 7 y se reemplaza por un 6. Luego se procede a la resta en el lugar de las centenas, donde 6 no es menor que 5, por lo que la diferencia se escribe en el lugar de las centenas del resultado. Ya hemos terminado, el resultado es 192.
El método austriaco no reduce el 7 a 6, sino que aumenta en uno la cifra de las centenas del sustraendo. Se hace una pequeña marca cerca o debajo de esta cifra (según la escuela). Luego se procede a la resta preguntando qué número, cuando se aumenta en 1 y se le suma 5, da como resultado 7. La respuesta es 1 y se escribe en el lugar de las centenas del resultado.
Existe una sutileza adicional en el método americano, ya que el estudiante siempre emplea una tabla de resta mental. El método austriaco a menudo anima al estudiante a utilizar mentalmente la tabla de adición a la inversa. En el ejemplo anterior, en lugar de sumar 1 a 5, obtener 6 y restarlo de 7, se le pide al estudiante que considere qué número, cuando se aumenta en 1 y se le suma 5, da como resultado 7.
Ejemplo: [ cita requerida ]
Ejemplo: [ cita requerida ]
En este método, cada dígito del sustraendo se resta del dígito superior comenzando de derecha a izquierda. Si el número superior es demasiado pequeño para restarle el número inferior, le sumamos 10; este 10 se "toma prestado" del dígito superior de la izquierda, al que restamos 1. Luego pasamos a restar el siguiente dígito y tomamos prestado según sea necesario, hasta que se hayan restado todos los dígitos. Ejemplo: [ cita requerida ]
Una variante del método americano donde todo préstamo se realiza antes de toda resta. [16]
Ejemplo:
El método de diferencias parciales se diferencia de otros métodos de sustracción vertical porque no se toman prestados ni se llevan. En su lugar, se colocan signos más o menos dependiendo de si el minuendo es mayor o menor que el sustraendo. La suma de las diferencias parciales es la diferencia total. [17]
Ejemplo:
En lugar de encontrar la diferencia dígito por dígito, uno puede contar los números entre el sustraendo y el minuendo. [18]
Ejemplo: 1234 − 567 = se puede encontrar siguiendo los siguientes pasos:
Sume el valor de cada paso para obtener la diferencia total: 3 + 30 + 400 + 234 = 667 .
Otro método útil para el cálculo mental es dividir la resta en pequeños pasos. [19]
Ejemplo: 1234 − 567 = se puede resolver de la siguiente manera:
El mismo método de cambio utiliza el hecho de que sumar o restar el mismo número del minuendo y del sustraendo no cambia el resultado. Uno simplemente suma la cantidad necesaria para obtener ceros en el sustraendo. [20]
Ejemplo:
"1234 − 567 =" se puede resolver de la siguiente manera: