Transversalidad (matemáticas)

En matemáticas , la transversalidad es una noción que describe cómo los espacios pueden cruzarse ; la transversalidad puede verse como lo "opuesto" de la tangencia y juega un papel en la posición general . Formaliza la idea de una intersección genérica en topología diferencial . Se define considerando las linealizaciones de los espacios que se cruzan en los puntos de intersección.

Definición

Curvas transversales en la superficie de una esfera.

Curvas no transversales en la superficie de una esfera.

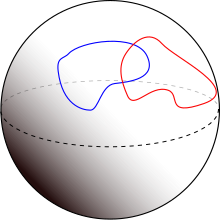
Se dice que dos subvariedades de una variedad suave de dimensión finita dada se cruzan transversalmente si en cada punto de intersección , sus espacios tangentes separados en ese punto generan juntos el espacio tangente de la variedad ambiental en ese punto. ^[1] Las variedades que no se cruzan son vacíamente transversales. Si las variedades son de dimensión complementaria (es decir, sus dimensiones suman la dimensión del espacio ambiental ), la condición significa que el espacio tangente a la variedad ambiental es la suma directa de los dos espacios tangentes más pequeños. Si una intersección es transversal, entonces la intersección será una subvariedad cuya codimensión es igual a las sumas de las codimensiones de las dos variedades. En ausencia de la condición de transversalidad, la intersección puede no ser una subvariedad y tener algún tipo de punto singular .

En particular, esto significa que las subvariedades transversales de dimensión complementaria se cruzan en puntos aislados (es decir, una variedad 0 ). Si ambas subvariedades y la variedad ambiental están orientadas , su intersección está orientada. Cuando la intersección es de dimensión cero, la orientación es simplemente más o menos para cada punto.

Una notación para la intersección transversal de dos subvariedades y de una variedad dada es . Esta notación se puede leer de dos maneras: ya sea como “ y se cruzan transversalmente” o como una notación alternativa para la intersección teórica de conjuntos de y cuando esa intersección es transversal. En esta notación, la definición de transversalidad dice ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$ ${\displaystyle M}$ ${\displaystyle L_{1}\pitchfork L_{2}}$ ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$ ${\displaystyle L_{1}\cap L_{2}}$ ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$

${\displaystyle L_{1}\pitchfork L_{2}\iff \forall p\in L_{1}\cap L_{2},T_{p}M=T_{p}L_{1}+T_{p}L_{2}.}$

Transversalidad de mapas

La noción de transversalidad de un par de subvariedades se extiende fácilmente a la transversalidad de una subvariedad y un mapa a la variedad ambiental, o a un par de mapas a la variedad ambiental, preguntando si los avances de los espacios tangentes a lo largo de la preimagen de puntos de intersección de las imágenes generan todo el espacio tangente de la variedad ambiental. ^[2] Si los mapas son incrustaciones , esto es equivalente a la transversalidad de subvariedades.

Significado de transversalidad para diferentes dimensiones

La transversalidad depende del espacio ambiental. Las dos curvas mostradas son transversales cuando se consideran incrustadas en el plano, pero no si las consideramos incrustadas en un plano en el espacio tridimensional.

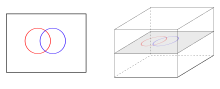
Supongamos que tenemos mapas transversales y donde y son variedades con dimensiones y respectivamente. ${\displaystyle f_{1}:L_{1}\to M}$ ${\displaystyle f_{2}:L_{2}\to M}$ ${\displaystyle L_{1},L_{2}}$ ${\displaystyle M}$ ${\displaystyle \ell _{1},\ell _{2}}$ ${\displaystyle m}$

El significado de transversalidad difiere mucho dependiendo de las dimensiones relativas de y . La relación entre transversalidad y tangencia es más clara cuando . ${\displaystyle M,L_{1}}$ ${\displaystyle L_{2}}$ ${\displaystyle \ell _{1}+\ell _{2}=m}$

Podemos considerar tres casos separados:

1. Cuando , es imposible que la imagen de los espacios tangentes de y abarque el espacio tangente de s en cualquier punto. Por tanto, cualquier intersección entre y no puede ser transversal. Sin embargo, las variedades que no se cruzan satisfacen vacíamente la condición, por lo que se puede decir que se cruzan transversalmente. ${\displaystyle \ell _{1}+\ell _{2}<m}$ ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$ ${\displaystyle M}$ ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$
2. Cuando , la imagen de los espacios tangentes de y debe sumar directamente al espacio tangente de s en cualquier punto de intersección. Por tanto, su intersección consta de puntos aislados con signo, es decir, una variedad de dimensión cero. ${\displaystyle \ell _{1}+\ell _{2}=m}$ ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$ ${\displaystyle M}$
3. Cuando esta suma no tiene por qué ser directa. De hecho no puede ser directo si y son inmersiones en su punto de intersección, como ocurre en el caso de las subvariedades incrustadas. Si los mapas son inmersiones, la intersección de sus imágenes será una multiplicidad de dimensiones. ${\displaystyle \ell _{1}+\ell _{2}>m}$ ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$ ${\displaystyle \ell _{1}+\ell _{2}-m.}$

Producto de intersección

Dadas dos subvariedades suaves cualesquiera, es posible perturbar cualquiera de ellas en una cantidad arbitrariamente pequeña de modo que la subvariedad resultante se cruce transversalmente con la subvariedad fija. Tales perturbaciones no afectan la clase de homología de las variedades ni de sus intersecciones. Por ejemplo, si variedades de dimensión complementaria se cruzan transversalmente, la suma con signo del número de sus puntos de intersección no cambia incluso si isotopizamos las variedades con otra intersección transversal. (Los puntos de intersección se pueden contar módulo 2, ignorando los signos, para obtener una invariante más burda). Esto desciende a un producto de intersección bilineal en clases de homología de cualquier dimensión, que es dual de Poincaré al producto de copa en cohomología . Al igual que el producto de copa, el producto de intersección es conmutativo graduado .

Ejemplos de intersecciones transversales.

El ejemplo no trivial más simple de transversalidad es el de los arcos en una superficie . Un punto de intersección entre dos arcos es transversal si y sólo si no es tangencia, es decir, sus rectas tangentes dentro del plano tangente a la superficie son distintas.

En un espacio tridimensional, las curvas transversales no se cruzan. Las curvas transversales a las superficies se cruzan en puntos y las superficies transversales entre sí se cruzan en curvas. Las curvas que son tangentes a una superficie en un punto (por ejemplo, curvas que se encuentran sobre una superficie) no intersecan la superficie transversalmente.

Aquí hay un ejemplo más especializado: supongamos que es un grupo de Lie simple y es su álgebra de Lie. Según el teorema de Jacobson-Morozov, todo elemento nilpotente puede incluirse en un triple . La teoría de la representación de nos dice que . El espacio es el espacio tangente a la órbita adjunta y, por lo tanto, el espacio afín cruza la órbita de transversalmente. El espacio se conoce como "rebanada de Slodowy" en honor a Peter Slodowy . ${\displaystyle G}$ ${\displaystyle {\mathfrak {g}}}$ ${\displaystyle e\in {\mathfrak {g}}}$ ${\displaystyle {\mathfrak {sl_{2}}}}$ ${\displaystyle (e,h,f)}$ ${\displaystyle {\mathfrak {sl_{2}}}}$ ${\displaystyle {\mathfrak {g}}=[{\mathfrak {g}},e]\oplus {\mathfrak {g}}_{f}}$ ${\displaystyle [{\mathfrak {g}},e]}$ ${\displaystyle e}$ ${\displaystyle {\rm {{Ad}(G)e}}}$ ${\displaystyle e+{\mathfrak {g}}_{f}}$ ${\displaystyle e}$ ${\displaystyle e+{\mathfrak {g}}_{f}}$

Aplicaciones

Control óptimo

En campos que utilizan el cálculo de variaciones o el principio máximo de Pontryagin relacionado , la condición de transversalidad se usa frecuentemente para controlar los tipos de soluciones encontradas en problemas de optimización. Por ejemplo, es una condición necesaria para las curvas solución de problemas de la forma:

Minimice cuando uno o ambos puntos finales de la curva no sean fijos. ${\displaystyle \int {F(x,y,y^{\prime })}dx}$

En muchos de estos problemas, la solución satisface la condición de que la curva de solución debe cruzar transversalmente la nulaclina o alguna otra curva que describa condiciones terminales.

Suavidad de los espacios de solución.

Utilizando el teorema de Sard , cuya hipótesis es un caso especial de la transversalidad de aplicaciones, se puede demostrar que las intersecciones transversales entre subvariedades de un espacio de dimensiones complementarias o entre subvariedades y aplicaciones de un espacio son en sí mismas subvariedades suaves. Por ejemplo, si una sección suave del paquete tangente de una variedad orientada , es decir, un campo vectorial , se ve como un mapa desde la base hasta el espacio total y corta la sección cero (vista como un mapa o como una subvariedad) transversalmente , entonces el conjunto cero de la sección, es decir, las singularidades del campo vectorial, forma una subvariedad suave de dimensión 0 de la base, es decir, un conjunto de puntos con signo. Los signos concuerdan con los índices del campo vectorial y, por tanto, la suma de los signos (es decir, la clase fundamental del conjunto cero) es igual a la característica de Euler de la variedad. De manera más general, para un paquete de vectores sobre una variedad de dimensión finita cerrada, suave y orientada, el conjunto cero de una sección transversal a la sección cero será una subvariedad de la base de codimensión igual al rango del paquete de vectores y su clase de homología. será Poincaré dual a la clase de Euler del paquete.

Un caso extremadamente especial de esto es el siguiente: si una función diferenciable de reales a reales tiene una derivada distinta de cero en un cero de la función, entonces el cero es simple, es decir, si la gráfica es transversal al eje x en ese cero; una derivada cero significaría una tangente horizontal a la curva, que concordaría con el espacio tangente al eje x .

Para un ejemplo de dimensión infinita, el operador de barra d es una sección de un determinado paquete espacial de Banach sobre el espacio de mapas desde una superficie de Riemann hasta una variedad casi compleja . El conjunto cero de esta sección consta de mapas holomorfos. Si se puede demostrar que el operador de barra d es transversal a la sección cero, este espacio de módulos será una variedad suave. Estas consideraciones juegan un papel fundamental en la teoría de curvas pseudoholomorfas y la teoría de Gromov-Witten . (¡Tenga en cuenta que para este ejemplo, la definición de transversalidad debe refinarse para poder tratar con espacios de Banach !)

Gramática

"Transversal" es un sustantivo; el adjetivo es "transversal".

cita de JHC Whitehead, 1959 ^[3]

Ver también

• Teorema de transversalidad

Notas

1. Guillemin y Pollack 1974, p.30.
2. Guillemin y Pollack 1974, p.28.
3. Hirsch (1976), página 66

Referencias

• Thom, René (1954). "Quelques propriétés globales des variétés diferenciables". Comentario. Matemáticas. Helv. 28 (1): 17–86. doi :10.1007/BF02566923. S2CID  120243638.
• Guillemin, Víctor; Pollack, Alan (1974). Topología diferencial . Prentice Hall. ISBN 0-13-212605-2.
• Hirsch, Morris (1976). Topología diferencial . Springer-Verlag. ISBN 0-387-90148-5.