Análisis de supervivencia

El análisis de supervivencia es una rama de la estadística que analiza la duración esperada del tiempo hasta que ocurre un evento, como la muerte en organismos biológicos o la falla en sistemas mecánicos. Este tema se llama teoría de la confiabilidad , análisis de la confiabilidad o ingeniería de la confiabilidad en ingeniería , análisis de la duración o modelado de la duración en economía y análisis del historial de eventos en sociología . El análisis de supervivencia intenta responder ciertas preguntas, como ¿cuál es la proporción de una población que sobrevivirá más allá de cierto tiempo? De los que sobreviven, ¿a qué tasa morirán o fallarán? ¿Se pueden tener en cuenta múltiples causas de muerte o falla? ¿Cómo aumentan o disminuyen las circunstancias o características particulares la probabilidad de supervivencia ?

Para responder a estas preguntas, es necesario definir el concepto de "duración de la vida". En el caso de la supervivencia biológica, la muerte es inequívoca, pero en el caso de la fiabilidad mecánica, el fallo puede no estar bien definido, ya que puede haber sistemas mecánicos en los que el fallo sea parcial, una cuestión de grado o no localizado en el tiempo . Incluso en los problemas biológicos, algunos acontecimientos (por ejemplo, un ataque cardíaco o una falla de otro órgano) pueden tener la misma ambigüedad. La teoría que se describe a continuación supone acontecimientos bien definidos en momentos específicos; otros casos pueden tratarse mejor con modelos que tengan en cuenta explícitamente los acontecimientos ambiguos.

En términos más generales, el análisis de supervivencia implica la modelización de los datos de tiempo hasta el evento; en este contexto, la muerte o el fracaso se consideran un "evento" en la literatura de análisis de supervivencia; tradicionalmente, solo ocurre un único evento para cada sujeto, después del cual el organismo o mecanismo muere o se rompe. Los modelos de eventos recurrentes o eventos repetidos flexibilizan ese supuesto. El estudio de eventos recurrentes es relevante en la confiabilidad de los sistemas y en muchas áreas de las ciencias sociales y la investigación médica.

Introducción al análisis de supervivencia

El análisis de supervivencia se utiliza de varias maneras:

Para describir los tiempos de supervivencia de los miembros de un grupo.
Para comparar los tiempos de supervivencia de dos o más grupos
- Prueba de rango logarítmico
Para describir el efecto de variables categóricas o cuantitativas sobre la supervivencia.
- Regresión de riesgos proporcionales de Cox
- Modelos paramétricos de supervivencia
- Árboles de supervivencia
- Bosques aleatorios de supervivencia

Definiciones de términos comunes en el análisis de supervivencia

Los siguientes términos se utilizan comúnmente en los análisis de supervivencia:

Evento: Muerte, aparición de una enfermedad, recurrencia de una enfermedad, recuperación u otra experiencia de interés.
Tiempo: El tiempo desde el comienzo de un período de observación (como una cirugía o el comienzo de un tratamiento) hasta (i) un evento, (ii) el final del estudio, o (iii) la pérdida de contacto o el retiro del estudio.
Censura / Observación censurada: La censura se produce cuando tenemos alguna información sobre el tiempo de supervivencia de un individuo, pero no sabemos exactamente el tiempo de supervivencia. El sujeto está censurado en el sentido de que no se observa ni se sabe nada sobre él después del tiempo de censura. Un sujeto censurado puede o no tener un evento después del final del tiempo de observación.
Función de supervivencia S(t): La probabilidad de que un sujeto sobreviva más tiempo que el tiempo t.

Ejemplo: Datos de supervivencia de la leucemia mieloide aguda

Este ejemplo utiliza el conjunto de datos de supervivencia de leucemia mielógena aguda "aml" del paquete "survival" de R. El conjunto de datos es de Miller (1997) ^[1] y la pregunta es si el tratamiento estándar de quimioterapia debería extenderse ('mantenerse') durante ciclos adicionales.

El conjunto de datos aml ordenados por tiempo de supervivencia se muestra en el cuadro.

El tiempo se indica mediante la variable "tiempo", que es el tiempo de supervivencia o censura.
El evento (recurrencia del cáncer de leucemia mieloide aguda) se indica mediante la variable "estado". 0 = sin evento (censurado), 1 = evento (recurrencia)
Grupo de tratamiento: la variable “x” indica si se administró quimioterapia de mantenimiento

La última observación (11), a las 161 semanas, está censurada. La censura indica que el paciente no tuvo un evento (no hubo recurrencia del cáncer de leucemia mieloide aguda). Otro sujeto, la observación 3, fue censurado a las 13 semanas (indicado por el estado = 0). Este sujeto estuvo en el estudio solo durante 13 semanas, y el cáncer de leucemia mieloide aguda no recurrió durante esas 13 semanas. Es posible que este paciente haya sido incluido cerca del final del estudio, de modo que pudiera ser observado solo durante 13 semanas. También es posible que el paciente haya sido incluido al principio del estudio, pero se haya perdido el seguimiento o se haya retirado del estudio. La tabla muestra que otros sujetos fueron censurados a las 16, 28 y 45 semanas (observaciones 17, 6 y 9 con estado = 0). Todos los sujetos restantes experimentaron eventos (recurrencia del cáncer de leucemia mieloide aguda) mientras estaban en el estudio. La pregunta de interés es si la recurrencia ocurre más tarde en los pacientes mantenidos que en los pacientes no mantenidos.

Diagrama de Kaplan-Meier para los datos de aml

La función de supervivencia S ( t ) es la probabilidad de que un sujeto sobreviva más tiempo que t . S ( t ) es teóricamente una curva suave, pero normalmente se estima utilizando la curva de Kaplan-Meier (KM). El gráfico muestra la curva de KM para los datos de aml y se puede interpretar de la siguiente manera:

El eje x es el tiempo, desde cero (cuando comenzó la observación) hasta el último punto de tiempo observado.
El eje y es la proporción de sujetos que sobreviven. En el momento cero, el 100 % de los sujetos están vivos sin que haya ocurrido ningún evento.
La línea continua (similar a una escalera) muestra la progresión de la ocurrencia de eventos.
Una caída vertical indica un evento. En la tabla de aml que se muestra arriba, dos sujetos tuvieron eventos a las cinco semanas, dos tuvieron eventos a las ocho semanas, uno tuvo un evento a las nueve semanas, y así sucesivamente. Estos eventos a las cinco semanas, ocho semanas, etc., se indican mediante caídas verticales en el gráfico KM en esos puntos temporales.
En el extremo derecho del gráfico KM hay una marca de verificación en las 161 semanas. La marca de verificación vertical indica que un paciente fue censurado en ese momento. En la tabla de datos aml, cinco sujetos fueron censurados, en las semanas 13, 16, 28, 45 y 161. Hay cinco marcas de verificación en el gráfico KM, que corresponden a estas observaciones censuradas.

Tabla de vida para los datos aml

Una tabla de vida resume los datos de supervivencia en términos de la cantidad de eventos y la proporción de sobrevivientes en cada punto temporal del evento. Se muestra la tabla de vida para los datos de aml, creada con el software R.

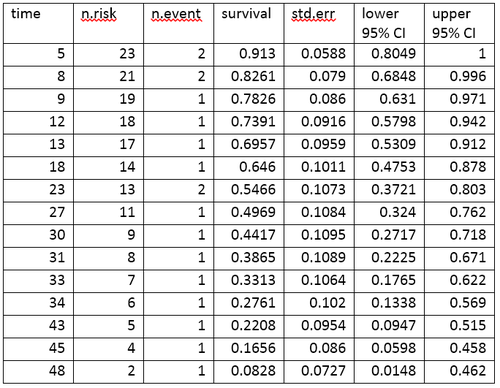
La tabla de vida resume los eventos y la proporción de sobrevivientes en cada momento del evento. Las columnas de la tabla de vida tienen la siguiente interpretación:

El tiempo da los puntos de tiempo en los que ocurren los eventos.
n.risk es el número de sujetos en riesgo inmediatamente antes del momento t. Estar "en riesgo" significa que el sujeto no ha tenido ningún evento antes del momento t y no está censurado antes o en el momento t.
n.event es el número de sujetos que tienen eventos en el tiempo t.
La supervivencia es la proporción de supervivientes, determinada mediante la estimación del límite del producto de Kaplan-Meier.
std.err es el error estándar de la supervivencia estimada. El error estándar de la estimación del límite del producto de Kaplan-Meier se calcula utilizando la fórmula de Greenwood y depende del número de personas en riesgo (n.riesgo en la tabla), el número de muertes (n.evento en la tabla) y la proporción de sobrevivientes (supervivencia en la tabla).
El IC del 95% inferior y el IC del 95% superior son los límites de confianza del 95% inferior y superior para la proporción de sobrevivientes.

Prueba de rangos logarítmicos: prueba de diferencias en la supervivencia en los datos de leucemia mieloide aguda

La prueba de rangos logarítmicos compara los tiempos de supervivencia de dos o más grupos. Este ejemplo utiliza una prueba de rangos logarítmicos para determinar la diferencia en la supervivencia entre los grupos de tratamiento mantenido y no mantenido en los datos de leucemia mieloide aguda. El gráfico muestra los gráficos de KM para los datos de leucemia mieloide aguda desglosados por grupo de tratamiento, lo que se indica mediante la variable "x" en los datos.

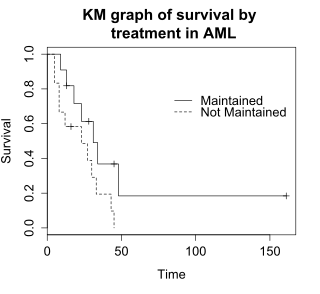
La hipótesis nula para una prueba de log-rank es que los grupos tienen la misma supervivencia. El número esperado de sujetos que sobreviven en cada punto temporal de cada uno se ajusta al número de sujetos en riesgo en los grupos en cada momento del evento. La prueba de log-rank determina si el número observado de eventos en cada grupo es significativamente diferente del número esperado. La prueba formal se basa en una estadística de chi-cuadrado. Cuando la estadística de log-rank es grande, es evidencia de una diferencia en los tiempos de supervivencia entre los grupos. La estadística de log-rank tiene aproximadamente una distribución de chi-cuadrado con un grado de libertad, y el valor p se calcula utilizando la prueba de chi-cuadrado .

Para los datos de ejemplo, la prueba de log-rank para la diferencia en supervivencia arroja un valor p de p=0,0653, lo que indica que los grupos de tratamiento no difieren significativamente en cuanto a supervivencia, suponiendo un nivel alfa de 0,05. El tamaño de la muestra de 23 sujetos es modesto, por lo que hay poco poder para detectar diferencias entre los grupos de tratamiento. La prueba de chi-cuadrado se basa en una aproximación asintótica, por lo que el valor p debe considerarse con cautela para tamaños de muestra pequeños .

Análisis de regresión de riesgos proporcionales (PH) de Cox

Las curvas de Kaplan-Meier y las pruebas de log-rank son más útiles cuando la variable predictora es categórica (p. ej., fármaco frente a placebo) o toma una pequeña cantidad de valores (p. ej., dosis de fármaco de 0, 20, 50 y 100 mg/día) que pueden tratarse como categóricas. La prueba de log-rank y las curvas KM no funcionan fácilmente con predictores cuantitativos como la expresión genética, el recuento de glóbulos blancos o la edad. Para las variables predictoras cuantitativas, un método alternativo es el análisis de regresión de riesgos proporcionales de Cox . Los modelos de Cox PH también funcionan con variables predictoras categóricas, que se codifican como variables indicadoras {0,1} o variables ficticias. La prueba de log-rank es un caso especial de un análisis de Cox PH y se puede realizar utilizando el software de Cox PH.

Ejemplo: análisis de regresión de riesgos proporcionales de Cox para el melanoma

Este ejemplo utiliza el conjunto de datos de melanoma del Capítulo 14 de Dalgaard. ^[2]

Los datos se encuentran en el paquete R ISwR. La regresión de riesgos proporcionales de Cox con R arroja los resultados que se muestran en el recuadro.

Los resultados de la regresión de Cox se interpretan de la siguiente manera.

El sexo se codifica como un vector numérico (1: femenino, 2: masculino). El resumen R del modelo de Cox proporciona el cociente de riesgo (HR) para el segundo grupo en relación con el primero, es decir, masculino frente a femenino.
coef = 0,662 es el logaritmo estimado del cociente de riesgo para hombres frente a mujeres.
exp(coef) = 1,94 = exp(0,662) - El logaritmo del cociente de riesgo (coef = 0,662) se transforma en el cociente de riesgo utilizando exp(coef). El resumen del modelo de Cox proporciona el cociente de riesgo para el segundo grupo en relación con el primero, es decir, hombres frente a mujeres. El cociente de riesgo estimado de 1,94 indica que los hombres tienen un mayor riesgo de muerte (menores tasas de supervivencia) que las mujeres, en estos datos.
se(coef) = 0,265 es el error estándar del logaritmo del cociente de riesgo.
z = 2,5 = coef/se(coef) = 0,662/0,265. Dividiendo el coef por su error estándar se obtiene la puntuación z.
p=0,013. El valor p correspondiente a z=2,5 para el sexo es p=0,013, lo que indica que existe una diferencia significativa en la supervivencia en función del sexo.

El resultado resumido también proporciona intervalos de confianza superior e inferior del 95 % para el cociente de riesgo: límite inferior del 95 % = 1,15; límite superior del 95 % = 3,26.

Finalmente, el resultado proporciona valores p para tres pruebas alternativas de significancia general del modelo:

Prueba de razón de verosimilitud = 6,15 en 1 gl, p = 0,0131
Prueba de Wald = 6,24 en 1 gl, p = 0,0125
Prueba de puntuación (log-rank) = 6,47 en 1 gl, p=0,0110

Estas tres pruebas son asintóticamente equivalentes. Para un N suficientemente grande, darán resultados similares. Para un N pequeño, pueden diferir un poco. La última fila, "Prueba de puntuación (logrank)" es el resultado de la prueba log-rank, con p=0,011, el mismo resultado que la prueba log-rank, porque la prueba log-rank es un caso especial de una regresión de Cox PH. La prueba de razón de verosimilitud tiene un mejor comportamiento para tamaños de muestra pequeños, por lo que generalmente se prefiere.

Modelo de Cox que utiliza una covariable en los datos de melanoma

El modelo de Cox extiende la prueba de log-rank al permitir la inclusión de covariables adicionales. ^[3] Este ejemplo utiliza el conjunto de datos de melanoma donde las variables predictoras incluyen una covariable continua, el grosor del tumor (nombre de la variable = "grueso").

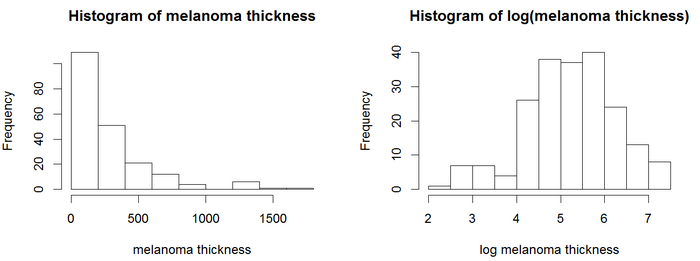
En los histogramas, los valores de espesor están sesgados positivamente y no tienen una distribución de probabilidad simétrica similar a la de Gauss . Los modelos de regresión, incluido el modelo de Cox, generalmente brindan resultados más confiables con variables distribuidas normalmente. ^[^{cita requerida}^] Para este ejemplo, podemos usar una transformación logarítmica . El logaritmo del espesor del tumor parece estar distribuido de manera más normal, por lo que los modelos de Cox usarán el logaritmo del espesor. El análisis de pH de Cox brinda los resultados en el recuadro.

El valor p para las tres pruebas generales (probabilidad, Wald y puntuación) es significativo, lo que indica que el modelo es significativo. El valor p para log(thick) es 6,9e-07, con un cociente de riesgo HR = exp(coef) = 2,18, lo que indica una fuerte relación entre el grosor del tumor y un mayor riesgo de muerte.

En cambio, el valor p para el sexo es ahora p=0,088. El cociente de riesgo HR = exp(coef) = 1,58, con un intervalo de confianza del 95% de 0,934 a 2,68. Como el intervalo de confianza para el HR incluye 1, estos resultados indican que el sexo hace una contribución menor a la diferencia en el HR después de controlar el grosor del tumor, y solo tiende hacia la significación. El examen de los gráficos de log(grosor) por sexo y una prueba t de log(grosor) por sexo indican que existe una diferencia significativa entre hombres y mujeres en el grosor del tumor cuando ven por primera vez al médico.

El modelo de Cox supone que los riesgos son proporcionales. La hipótesis de riesgo proporcional se puede probar utilizando la función R cox.zph(). Un valor p inferior a 0,05 indica que los riesgos no son proporcionales. Para los datos de melanoma obtenemos p=0,222. Por lo tanto, no podemos rechazar la hipótesis nula de que los riesgos sean proporcionales. En los libros de texto citados se describen pruebas y gráficos adicionales para examinar un modelo de Cox.

Extensiones a los modelos de Cox

Los modelos de Cox se pueden ampliar para abordar variaciones en el análisis simple.

Estratificación. Los sujetos se pueden dividir en estratos, donde se espera que los sujetos dentro de un estrato sean relativamente más similares entre sí que con sujetos elegidos al azar de otros estratos. Se supone que los parámetros de regresión son los mismos en todos los estratos, pero puede existir un riesgo de referencia diferente para cada estrato. La estratificación es útil para los análisis que utilizan sujetos emparejados, para tratar con subconjuntos de pacientes, como diferentes clínicas, y para tratar las violaciones del supuesto de riesgo proporcional.
Covariables que varían con el tiempo. Algunas variables, como el género y el grupo de tratamiento, generalmente permanecen invariables en un ensayo clínico. Otras variables clínicas, como los niveles de proteínas séricas o la dosis de medicamentos concomitantes, pueden cambiar a lo largo de un estudio. Los modelos de Cox pueden ampliarse para estas covariables que varían con el tiempo.

Modelos de supervivencia estructurados en forma de árbol

El modelo de regresión de Cox PH es un modelo lineal. Es similar a la regresión lineal y a la regresión logística. En concreto, estos métodos suponen que una única línea, curva, plano o superficie es suficiente para separar grupos (vivos, muertos) o para estimar una respuesta cuantitativa (tiempo de supervivencia).

En algunos casos, las particiones alternativas brindan una clasificación o estimaciones cuantitativas más precisas. Un conjunto de métodos alternativos son los modelos de supervivencia estructurados en árbol ^[4]^[5]^[6], incluidos los bosques aleatorios de supervivencia. ^[7] Los modelos de supervivencia estructurados en árbol pueden brindar predicciones más precisas que los modelos de Cox. Examinar ambos tipos de modelos para un conjunto de datos determinado es una estrategia razonable.

Ejemplo de análisis de árbol de supervivencia

Este ejemplo de análisis de árbol de supervivencia utiliza el paquete R "rpart". ^[8] El ejemplo se basa en 146 pacientes con cáncer de próstata en estadio C del conjunto de datos stagec en rpart. Rpart y el ejemplo stagec se describen en Atkinson y Therneau (1997), ^[9] que también se distribuye como una viñeta del paquete rpart. ^[8]

Las variables en etapas son:

pgtime : tiempo hasta la progresión, o último seguimiento libre de progresión
pgstat : estado en el último seguimiento (1=progresado, 0=censurado)
edad : edad en el momento del diagnóstico
eet : terapia endocrina temprana (1=no, 0=sí)
Ploidía : patrón de ADN diploide/tetraploide/aneuploide
g2 : % de células en fase G2
grado : grado del tumor (1-4)
Gleason : Grado Gleason (3-10)

El árbol de supervivencia producido por el análisis se muestra en la figura.

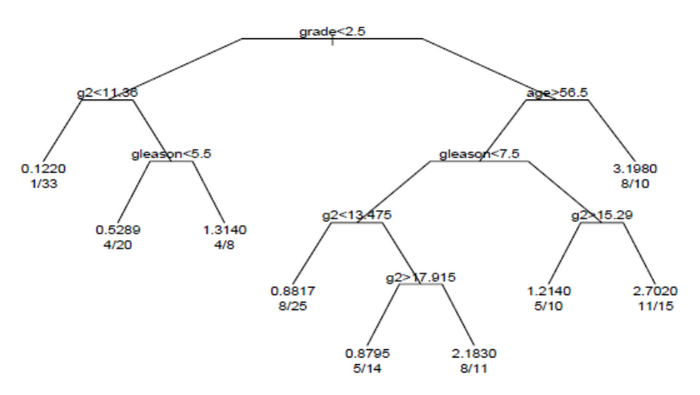
Cada rama del árbol indica una división en el valor de una variable. Por ejemplo, la raíz del árbol divide a los sujetos con una calificación < 2,5 frente a los sujetos con una calificación 2,5 o superior. Los nodos terminales indican la cantidad de sujetos del nodo, la cantidad de sujetos que tienen eventos y la tasa relativa de eventos en comparación con la raíz. En el nodo del extremo izquierdo, los valores 1/33 indican que uno de los 33 sujetos del nodo tuvo un evento y que la tasa relativa de eventos es 0,122. En el nodo del extremo inferior derecho, los valores 11/15 indican que 11 de los 15 sujetos del nodo tuvieron un evento y la tasa relativa de eventos es 2,7.

Bosques aleatorios de supervivencia

Una alternativa a la construcción de un único árbol de supervivencia es construir muchos árboles de supervivencia, donde cada árbol se construye utilizando una muestra de los datos y se promedian los árboles para predecir la supervivencia. ^[7] Este es el método subyacente a los modelos de bosque aleatorio de supervivencia. El análisis de bosque aleatorio de supervivencia está disponible en el paquete R "randomForestSRC". ^[10]

El paquete randomForestSRC incluye un ejemplo de análisis de bosque aleatorio de supervivencia utilizando el conjunto de datos pbc. Estos datos proceden del ensayo de cirrosis biliar primaria (CBP) de la Clínica Mayo realizado entre 1974 y 1984. En el ejemplo, el modelo de supervivencia de bosque aleatorio proporciona predicciones de supervivencia más precisas que el modelo de PH de Cox. Los errores de predicción se calculan mediante un nuevo muestreo bootstrap .

Modelos de supervivencia de aprendizaje profundo

Los avances recientes en el aprendizaje de representaciones profundas se han extendido a la estimación de supervivencia. El modelo DeepSurv ^[11] propone reemplazar la parametrización log-lineal del modelo CoxPH con un perceptrón multicapa. Otras extensiones como Deep Survival Machines ^[12] y Deep Cox Mixtures ^[13] implican el uso de modelos de mezcla de variables latentes para modelar la distribución del tiempo hasta el evento como una mezcla de distribuciones paramétricas o semiparamétricas mientras se aprenden conjuntamente representaciones de las covariables de entrada. Los enfoques de aprendizaje profundo han demostrado un rendimiento superior, especialmente en modalidades de datos de entrada complejos, como imágenes y series temporales clínicas.

Formulación general

Función de supervivencia

El objeto de interés principal es la función de supervivencia , convencionalmente denominada S , que se define como

$S(t)=\Pr(T>t)$ donde t es un tiempo, T es una variable aleatoria que denota el momento de la muerte y "Pr" representa la probabilidad . Es decir, la función de supervivencia es la probabilidad de que el momento de la muerte sea posterior a un tiempo especificado t . La función de supervivencia también se denomina función de supervivencia o función de supervivencia en problemas de supervivencia biológica, y función de confiabilidad en problemas de supervivencia mecánica. En este último caso, la función de confiabilidad se denota R ( t ).

Generalmente se supone que S (0) = 1, aunque podría ser menor que 1 si existe la posibilidad de muerte o falla inmediata.

La función de supervivencia debe ser no creciente: S ( u ) ≤ S ( t ) si u ≥ t . Esta propiedad se deduce directamente porque T > u implica T > t . Esto refleja la noción de que la supervivencia hasta una edad posterior es posible solo si se alcanzan todas las edades más jóvenes. Dada esta propiedad, la función de distribución de la vida útil y la densidad de eventos ( F y f a continuación) están bien definidas.

Generalmente se supone que la función de supervivencia se acerca a cero a medida que aumenta la edad sin límite (es decir, S ( t ) → 0 cuando t → ∞), aunque el límite podría ser mayor que cero si es posible la vida eterna. Por ejemplo, podríamos aplicar el análisis de supervivencia a una mezcla de isótopos de carbono estables e inestables ; los isótopos inestables se desintegrarían tarde o temprano, pero los isótopos estables durarían indefinidamente.

Función de distribución de la duración de vida y densidad de eventos

Las cantidades relacionadas se definen en términos de la función de supervivencia.

La función de distribución de vida útil , convencionalmente denominada F , se define como el complemento de la función de supervivencia,

$F(t)=\Pr(T\leq t)=1-S(t).$ Si F es diferenciable , entonces la derivada, que es la función de densidad de la distribución de vida útil, se denota convencionalmente f ,

$f(t)=F'(t)={\frac {d}{dt}}F(t).$ La función f a veces se denomina densidad de eventos ; es la tasa de eventos de muerte o falla por unidad de tiempo.

La función de supervivencia se puede expresar en términos de funciones de distribución de probabilidad y de densidad de probabilidad.

$S(t)=\Pr(T>t)=\int _{t}^{\infty }f(u)\,du=1-F(t).$ De manera similar, una función de densidad de eventos de supervivencia se puede definir como

$s(t)=S'(t)={\frac {d}{dt}}S(t)={\frac {d}{dt}}\int _{t}^{\infty }f(u)\,du={\frac {d}{dt}}[1-F(t)]=-f(t).$ En otros campos, como la física estadística, la función de densidad de eventos de supervivencia se conoce como densidad de tiempo de primer paso .

Función de riesgo y función de riesgo acumulativo

La función de riesgo , convencionalmente denominada como , se define como la tasa de eventos en el momento condicional a la supervivencia hasta el momento o más tarde (es decir, ). Supongamos que un elemento ha sobrevivido durante un tiempo y deseamos la probabilidad de que no sobreviva durante un tiempo adicional : $\lambda$ $h$ $t$ $t$ $T\geq t$ $t$ $dt$

$h(t)=\lim _{dt\rightarrow 0}{\frac {\Pr(t\leq T<t+dt)}{dt\cdot S(t)}}={\frac {f(t)}{S(t)}}=-{\frac {S'(t)}{S(t)}}.$ La fuerza de mortalidad es un sinónimo de función de riesgo que se utiliza particularmente en demografía y ciencia actuarial , donde se denota por . El término tasa de riesgo es otro sinónimo. $\mu$

La fuerza de mortalidad de la función de supervivencia se define como $\mu (x)=-{d \over dx}\ln(S(x))={\frac {f(x)}{S(x)}}$

La fuerza de la mortalidad también se denomina fuerza del fracaso. Es la función de densidad de probabilidad de la distribución de la mortalidad.

En la ciencia actuarial, la tasa de riesgo es la tasa de muerte para las personas mayores de . Para una persona mayor de , la fuerza de mortalidad años después es la fuerza de mortalidad para una persona de – años. La tasa de riesgo también se denomina tasa de fracaso. La tasa de riesgo y la tasa de fracaso son nombres que se utilizan en la teoría de la confiabilidad. $x$ $x$ $t$ $(x+t)$

Cualquier función es una función de riesgo si y sólo si satisface las siguientes propiedades: $h$

$\forall x\geq 0\left(h(x)\geq 0\right)$ ,
$\int _{0}^{\infty }h(x)dx=\infty$ .

De hecho, la tasa de riesgo suele ser más informativa acerca del mecanismo subyacente del fallo que las otras representaciones de una distribución a lo largo de la vida.

La función de riesgo debe ser no negativa, , y su integral debe ser infinita, pero no está restringida de ninguna otra manera; puede ser creciente o decreciente, no monótona o discontinua. Un ejemplo es la función de riesgo de la curva de la bañera , que es grande para valores pequeños de , decreciente hasta un mínimo y luego creciente nuevamente; esto puede modelar la propiedad de algunos sistemas mecánicos de fallar poco después de la operación o mucho más tarde, a medida que el sistema envejece. $\lambda (t)\geq 0$ $[0,\infty ]$ $t$

La función de riesgo se puede representar alternativamente en términos de la función de riesgo acumulativo , denotada convencionalmente como : $\Lambda$ $H$

$\,\Lambda (t)=-\log S(t)$ Así que transponiendo signos y exponenciando

$\,S(t)=\exp(-\Lambda (t))$ o diferenciando (con la regla de la cadena)

${\frac {d}{dt}}\Lambda (t)=-{\frac {S'(t)}{S(t)}}=\lambda (t).$ El nombre "función de riesgo acumulativo" se deriva del hecho de que

$\Lambda (t)=\int _{0}^{t}\lambda (u)\,du$ que es la “acumulación” del peligro a lo largo del tiempo.

De la definición de , vemos que aumenta sin límite cuando t tiende a infinito (suponiendo que tiende a cero). Esto implica que no debe disminuir demasiado rápido, ya que, por definición, el riesgo acumulado tiene que divergir. Por ejemplo, no es la función de riesgo de ninguna distribución de supervivencia, porque su integral converge a 1. $\Lambda (t)$ $S(t)$ $\lambda (t)$ $\exp(-t)$

La función de supervivencia , la función de riesgo acumulativo , la densidad , la función de riesgo y la función de distribución de vida útil están relacionadas a través de $S(t)$ $\Lambda (t)$ $f(t)$ $\lambda (t)$ $F(t)$ $S(t)=\exp[-\Lambda (t)]={\frac {f(t)}{\lambda (t)}}=1-F(t),\quad t>0.$

Magnitudes derivadas de la distribución de supervivencia

La vida futura en un momento dado es el tiempo restante hasta la muerte, dada la supervivencia hasta la edad . Por lo tanto, está en la notación actual. La vida futura esperada es el valor esperado de la vida futura. La probabilidad de muerte a la edad o antes , dada la supervivencia hasta la edad , es simplemente $t_{0}$ $t_{0}$ $T-t_{0}$ $t_{0}+t$ $t_{0}$

$P(T\leq t_{0}+t\mid T>t_{0})={\frac {P(t_{0}<T\leq t_{0}+t)}{P(T>t_{0})}}={\frac {F(t_{0}+t)-F(t_{0})}{S(t_{0})}}.$ Por lo tanto, la densidad de probabilidad de la vida futura es

${\frac {d}{dt}}{\frac {F(t_{0}+t)-F(t_{0})}{S(t_{0})}}={\frac {f(t_{0}+t)}{S(t_{0})}}$ y la vida útil futura esperada es

${\frac {1}{S(t_{0})}}\int _{0}^{\infty }t\,f(t_{0}+t)\,dt={\frac {1}{S(t_{0})}}\int _{t_{0}}^{\infty }S(t)\,dt,$ donde la segunda expresión se obtiene mediante integración por partes .

Porque , es decir, al nacer, esto se reduce al tiempo de vida esperado. $t_{0}=0$

En los problemas de confiabilidad, la vida útil esperada se denomina tiempo medio hasta el fallo , y la vida útil futura esperada se denomina vida útil residual media .

Como la probabilidad de que un individuo sobreviva hasta la edad t o más es S ( t ), por definición, el número esperado de sobrevivientes a la edad t de una población inicial de n recién nacidos es n × S ( t ), asumiendo la misma función de supervivencia para todos los individuos. Por lo tanto, la proporción esperada de sobrevivientes es S ( t ). Si la supervivencia de diferentes individuos es independiente, el número de sobrevivientes a la edad t tiene una distribución binomial con parámetros n y S ( t ), y la varianza de la proporción de sobrevivientes es S ( t ) × (1- S ( t ))/ n .

La edad a la que sobreviven una determinada proporción de supervivientes se puede determinar resolviendo la ecuación S ( t ) = q para t , donde q es el cuantil en cuestión. Normalmente, se interesa por la mediana de vida , para la que q = 1/2, u otros cuantiles como q = 0,90 o q = 0,99.

Censura

La censura es una forma de problema de datos faltantes en el que no se observa el tiempo transcurrido hasta el evento por razones como la finalización del estudio antes de que todos los sujetos reclutados hayan mostrado el evento de interés o el sujeto haya abandonado el estudio antes de experimentar un evento. La censura es común en el análisis de supervivencia.

Si solo se conoce el límite inferior l para el tiempo real del evento T , de modo que T > l , esto se denomina censura derecha . La censura derecha se producirá, por ejemplo, para aquellos sujetos cuya fecha de nacimiento se conoce, pero que aún están vivos cuando se pierden para el seguimiento o cuando finaliza el estudio. Generalmente nos encontramos con datos censurados por la derecha.

Si el evento de interés ya ocurrió antes de que el sujeto fuera incluido en el estudio pero no se sabe cuándo ocurrió, se dice que los datos están censurados por la izquierda . ^[14] Cuando solo se puede decir que el evento ocurrió entre dos observaciones o exámenes, esto es censura de intervalo .

La censura a la izquierda se produce, por ejemplo, cuando un diente permanente ya ha salido antes de que se inicie un estudio odontológico cuyo objetivo es estimar la distribución de su aparición. En el mismo estudio, se censura el intervalo de tiempo de aparición cuando el diente permanente está presente en la boca en el examen actual pero todavía no en el examen anterior. La censura a intervalos se produce a menudo en los estudios sobre el VIH/SIDA. De hecho, el tiempo hasta la seroconversión al VIH solo se puede determinar mediante una evaluación de laboratorio que generalmente se inicia después de una visita al médico. En ese caso, solo se puede concluir que la seroconversión al VIH se ha producido entre dos exámenes. Lo mismo se aplica al diagnóstico del SIDA, que se basa en los síntomas clínicos y debe confirmarse mediante un examen médico.

También puede ocurrir que los sujetos con una vida útil inferior a un cierto umbral no sean observados en absoluto: esto se llama truncamiento . Obsérvese que el truncamiento es diferente de la censura a la izquierda, ya que para un dato censurado a la izquierda, sabemos que el sujeto existe, pero para un dato truncado, podemos ignorar por completo al sujeto. El truncamiento también es común. En un llamado estudio de entrada retrasada , los sujetos no son observados en absoluto hasta que han alcanzado una cierta edad. Por ejemplo, es posible que las personas no sean observadas hasta que hayan alcanzado la edad para ingresar a la escuela. Cualquier sujeto fallecido en el grupo de edad preescolar sería desconocido. Los datos truncados a la izquierda son comunes en el trabajo actuarial para seguros de vida y pensiones . ^[15]

Los datos censurados a la izquierda pueden aparecer cuando el tiempo de supervivencia de una persona se vuelve incompleto en el lado izquierdo del período de seguimiento de la misma. Por ejemplo, en un ejemplo epidemiológico, podemos hacer un seguimiento de un paciente para detectar un trastorno infeccioso a partir del momento en que da positivo en la prueba de la infección. Aunque podemos conocer el lado derecho de la duración de interés, es posible que nunca sepamos el tiempo exacto de exposición al agente infeccioso. ^[16]

Ajuste de parámetros a los datos

Los modelos de supervivencia pueden considerarse modelos de regresión ordinarios en los que la variable de respuesta es el tiempo. Sin embargo, el cálculo de la función de verosimilitud (necesaria para ajustar parámetros o hacer otros tipos de inferencias) se complica por la censura. La función de verosimilitud para un modelo de supervivencia, en presencia de datos censurados, se formula de la siguiente manera. Por definición, la función de verosimilitud es la probabilidad condicional de los datos dados los parámetros del modelo. Es habitual suponer que los datos son independientes dados los parámetros. Entonces, la función de verosimilitud es el producto de la verosimilitud de cada dato. Es conveniente dividir los datos en cuatro categorías: sin censura, censurados por la izquierda, censurados por la derecha y censurados por intervalo. Estas se denotan "unc.", "lc", "rc" e "ic" en la ecuación siguiente.

$L(\theta )=\prod _{T_{i}\in unc.}\Pr(T=T_{i}\mid \theta )\prod _{i\in l.c.}\Pr(T<T_{i}\mid \theta )\prod _{i\in r.c.}\Pr(T>T_{i}\mid \theta )\prod _{i\in i.c.}\Pr(T_{i,l}<T<T_{i,r}\mid \theta ).$ Para datos sin censura, con igual edad al momento de la muerte, tenemos $T_{i}$

$\Pr(T=T_{i}\mid \theta )=f(T_{i}\mid \theta ).$ Para los datos censurados a la izquierda, de modo que se sabe que la edad al momento de la muerte es menor que , tenemos $T_{i}$

$\Pr(T<T_{i}\mid \theta )=F(T_{i}\mid \theta )=1-S(T_{i}\mid \theta ).$ Para los datos censurados a la derecha, de modo que se sabe que la edad al momento de la muerte es mayor que , tenemos $T_{i}$

$\Pr(T>T_{i}\mid \theta )=1-F(T_{i}\mid \theta )=S(T_{i}\mid \theta ).$ Para un dato censurado por intervalo, tal que se sabe que la edad al momento de la muerte es menor que y mayor que , tenemos $T_{i,r}$ $T_{i,l}$

$\Pr(T_{i,l}<T<T_{i,r}\mid \theta )=S(T_{i,l}\mid \theta )-S(T_{i,r}\mid \theta ).$ Una aplicación importante donde surgen datos censurados por intervalos son los datos de estado actual, donde se sabe que un evento no ocurrió antes de un tiempo de observación y que ocurrió antes del siguiente tiempo de observación. $T_{i}$

Estimación no paramétrica

El estimador de Kaplan-Meier se puede utilizar para estimar la función de supervivencia. El estimador de Nelson-Aalen se puede utilizar para proporcionar una estimación no paramétrica de la función de tasa de riesgo acumulada. Estos estimadores requieren datos de toda la vida. Los recuentos periódicos de casos (cohortes) y muertes (y recuperación) son estadísticamente suficientes para realizar estimaciones no paramétricas de máxima verosimilitud y mínimos cuadrados de las funciones de supervivencia, sin datos de toda la vida.

Modelos de supervivencia en tiempo discreto

Si bien muchos modelos pramétricos asumen un tiempo continuo, los modelos de supervivencia de tiempo discreto se pueden mapear a un problema de clasificación binaria. En un modelo de supervivencia de tiempo discreto, el período de supervivencia se remuestrea artificialmente en intervalos donde para cada intervalo se registra un indicador objetivo binario si el evento tiene lugar en un cierto horizonte de tiempo. ^{[17] Si}se calibra un clasificador binario (potencialmente mejorado con una probabilidad diferente para tener más en cuenta la estructura del problema) , entonces la puntuación del clasificador es la función de riesgo (es decir, la probabilidad condicional de falla). ^[17]

Los modelos de supervivencia en tiempo discreto están conectados con la probabilidad empírica . ^[18]^[19]

Bondad de ajuste

La bondad de ajuste de los modelos de supervivencia se puede evaluar utilizando reglas de puntuación . ^[20]

Software informático para análisis de supervivencia

El libro de texto de Kleinbaum tiene ejemplos de análisis de supervivencia utilizando SAS, R y otros paquetes. ^[21] Los libros de texto de Brostrom, ^[22] Dalgaard ^[2] y Tableman y Kim ^[23] dan ejemplos de análisis de supervivencia utilizando R (o utilizando S, y que se ejecutan en R).

Distribuciones utilizadas en el análisis de supervivencia

Aplicaciones

Riesgo de crédito ^[24]^[25]
Tasa de condenas falsas de reclusos condenados a muerte ^[26]
Plazos de entrega de componentes metálicos en la industria aeroespacial ^[27]
Predictores de reincidencia delictiva ^[28]
Distribución de supervivencia de animales marcados con radio ^[29]
Muerte violenta de los emperadores romanos en el tiempo ^[30]
Tiempos de espera entre transacciones de acciones negociadas electrónicamente en una bolsa de valores ^[31]

Véase también

Referencias

^ Miller, Rupert G. (1997), Análisis de supervivencia , John Wiley & Sons, ISBN 0-471-25218-2
^ ab Dalgaard, Peter (2008), Introducción a la estadística con R (segunda edición), Springer, ISBN 978-0387790534
^ Saegusa, Takumi; Di, Chongzhi; Chen, Ying Qing (septiembre de 2014). "Prueba de hipótesis para un modelo de Cox extendido con coeficientes que varían en el tiempo". Biometrics . 70 (3): 619–628. doi :10.1111/biom.12185. ISSN 0006-341X. PMC 4247822 .
^ Segal, Mark Robert (1988). "Árboles de regresión para datos censurados". Biometrics . 44 (1): 35–47. doi :10.2307/2531894. JSTOR 2531894. S2CID 60974957.
^ Leblanc, Michael; Crowley, John (1993). "Árboles de supervivencia por bondad de división". Revista de la Asociación Estadounidense de Estadística . 88 (422): 457–467. doi :10.1080/01621459.1993.10476296. ISSN 0162-1459.
^ Ritschard, Gilbert; Gabadinho, Alexis; Muller, Nicolas S.; Studer, Matthias (2008). "Historias de eventos mineros: una perspectiva de las ciencias sociales". Revista internacional de minería de datos, modelado y gestión . 1 (1): 68. doi :10.1504/IJDMMM.2008.022538. ISSN 1759-1163.
^ ab Ishwaran, Hemant; Kogalur, Udaya B.; Blackstone, Eugene H.; Lauer, Michael S. (1 de septiembre de 2008). "Bosques de supervivencia aleatorios". Anales de estadística aplicada . 2 (3). arXiv : 0811.1645 . doi : 10.1214/08-AOAS169 . ISSN 1932-6157. S2CID 2003897.
^ ab Therneau, Terry J.; Atkinson, Elizabeth J. "rpart: Particionamiento recursivo y árboles de regresión". CRAN . Consultado el 12 de noviembre de 2021 .
^ Atkinson, Elizabeth J.; Therneau, Terry J. (1997). Introducción al particionamiento recursivo mediante las rutinas RPART. Mayo Foundation.
^ Ishwaran, Hemant; Kogalur, Udaya B. "randomForestSRC: Bosques aleatorios unificados rápidos para supervivencia, regresión y clasificación (RF-SRC)". CRAN . Consultado el 12 de noviembre de 2021 .
^ Singh, Jared; Katzman, L. (2018). "DeepSurv: sistema de recomendación de tratamiento personalizado que utiliza una red neuronal profunda de riesgos proporcionales de Cox". Metodología de investigación médica de BMC .
^ Nagpal, Chirag (2021). "Máquinas de supervivencia profunda: regresión de supervivencia totalmente paramétrica y aprendizaje de representación para datos censurados con riesgos competitivos". Revista IEEE de informática biomédica y sanitaria . 25 (8): 3163–3175. arXiv : 2003.01176 . doi :10.1109/JBHI.2021.3052441. PMID 33460387. S2CID 211817982.
^ Nagpal, Chirag (2021). "Mezclas de Cox profundas para la regresión de supervivencia". Conferencia sobre aprendizaje automático para la atención médica . arXiv : 2101.06536 .
^ Darity, William A. Jr., ed. (2008). "Censura, izquierda y derecha". Enciclopedia Internacional de las Ciencias Sociales . Vol. 1 (2.ª ed.). Macmillan. págs. 473–474 . Consultado el 6 de noviembre de 2016 .
^ Richards, SJ (2012). "Un manual de modelos de supervivencia paramétricos para uso actuarial". Scandinavian Actuarial Journal . 2012 (4): 233–257. doi :10.1080/03461238.2010.506688. S2CID 119577304.
^ Singh, R.; Mukhopadhyay, K. (2011). "Análisis de supervivencia en ensayos clínicos: aspectos básicos y áreas que se deben conocer". Perspect Clin Res . 2 (4): 145–148. doi : 10.4103/2229-3485.86872 . PMC 3227332 . PMID 22145125.
^ ab Suresh, K., Severn, C. y Ghosh, D. Modelos de predicción de supervivencia: una introducción al modelado de tiempo discreto. BMC Med Res Methodol 22, 207 (2022). https://doi.org/10.1186/s12874-022-01679-6 , https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/s12874-022-01679-6
^ Probabilidad empírica en el análisis de supervivencia, Gang Li (EE. UU.), Runze Li (EE. UU.) y Mai Zhou (EE. UU.), Análisis multivariante contemporáneo y diseño de experimentos. Marzo de 2005, 337-349, https://www.ms.uky.edu/~mai/research/llz.pdf
^ La función de distribución empírica con datos agrupados, censurados y truncados arbitrariamente, Bruce W. Turnbull, Journal of the Royal Statistical Society. Serie B (Metodológica) Vol. 38, N.º 3 (1976), págs. 290-295 (6 páginas), https://apps.dtic.mil/sti/tr/pdf/ADA030940.pdf
^ Reglas de puntuación adecuadas para el análisis de supervivencia, Hiroki Yanagisawa, https://arxiv.org/abs/2305.00621v3
^ Kleinbaum, David G.; Klein, Mitchel (2012), Análisis de supervivencia: un texto de autoaprendizaje (tercera edición), Springer, ISBN 978-1441966452
^ Brostrom, Göran (2012), Análisis del historial de eventos con R (primera edición), Chapman & Hall/CRC, ISBN 978-1439831649
^ Tableman, Mara; Kim, Jong Sung (2003), Análisis de supervivencia utilizando S (Primera edición), Chapman y Hall/CRC, ISBN 978-1584884088
^ Stepanova, Maria; Thomas, Lyn (1 de abril de 2002). "Métodos de análisis de supervivencia para datos de préstamos personales". Investigación de operaciones . 50 (2): 277–289. doi :10.1287/opre.50.2.277.426. ISSN 0030-364X.
^ Glennon, Dennis; Nigro, Peter (2005). "Medición del riesgo de impago de los préstamos a pequeñas empresas: un enfoque de análisis de supervivencia". Journal of Money, Credit and Banking . 37 (5): 923–947. doi :10.1353/mcb.2005.0051. ISSN 0022-2879. JSTOR 3839153. S2CID 154615623.
^ Kennedy, Edward H.; Hu, Chen; O'Brien, Barbara; Gross, Samuel R. (20 de mayo de 2014). "Tasa de condenas falsas de acusados penales que son sentenciados a muerte". Actas de la Academia Nacional de Ciencias . 111 (20): 7230–7235. Bibcode :2014PNAS..111.7230G. doi : 10.1073/pnas.1306417111 . ISSN 0027-8424. PMC 4034186 . PMID 24778209.
^ de Cos Juez, FJ; García Nieto, PJ; Martínez Torres, J.; Taboada Castro, J. (2010-10-01). "Análisis de tiempos de entrega de componentes metálicos en la industria aeroespacial mediante un modelo de máquina vectorial soportada". Modelado matemático y computacional . Modelos matemáticos en medicina, negocios e ingeniería 2009. 52 (7): 1177–1184. doi : 10.1016/j.mcm.2010.03.017 . ISSN 0895-7177.
^ Spivak, Andrew L.; Damphousse, Kelly R. (2006). "¿Quién vuelve a prisión? Un análisis de supervivencia de la reincidencia entre los delincuentes adultos liberados en Oklahoma, 1985-2004". Investigación y política de justicia . 8 (2): 57–88. doi :10.3818/jrp.8.2.2006.57. ISSN 1525-1071. S2CID 144566819.
^ Pollock, Kenneth H.; Winterstein, Scott R.; Bunck, Christine M.; Curtis, Paul D. (1989). "Análisis de supervivencia en estudios de telemetría: el diseño de entrada escalonada". Revista de gestión de la vida silvestre . 53 (1): 7–15. doi :10.2307/3801296. ISSN 0022-541X. JSTOR 3801296.
^ Saleh, Joseph Homer (23 de diciembre de 2019). «Análisis de fiabilidad estadística para una ocupación muy peligrosa: emperador romano». Palgrave Communications . 5 (1): 1–7. doi : 10.1057/s41599-019-0366-y . ISSN 2055-1045.
^ Kreer, Markus; Kizilersu, Ayse; Thomas, Anthony W. (2022). "Algoritmo de maximización de expectativas censuradas para mezclas: aplicación a tiempos de espera entre transacciones". Physica A: Mecánica estadística y sus aplicaciones . 587 (1): 126456. Bibcode :2022PhyA..58726456K. doi :10.1016/j.physa.2021.126456. ISSN 0378-4371. S2CID 244198364.

Lectura adicional

Collett, David (2003). Modelado de datos de supervivencia en la investigación médica (segunda edición). Boca Raton: Chapman & Hall/CRC. ISBN 1584883251.
Elandt-Johnson, Regina; Johnson, Norman (1999). Modelos de supervivencia y análisis de datos . Nueva York: John Wiley & Sons. ISBN 0471349925.
Kalbfleisch, JD; Prentice, Ross L. (2002). El análisis estadístico de los datos del tiempo de falla . Nueva York: John Wiley & Sons. ISBN 047136357X.
Lawless, Jerald F. (2003). Modelos y métodos estadísticos para datos de vida (2.ª ed.). Hoboken: John Wiley and Sons. ISBN 0471372153.
Rausand, M.; Hoyland, A. (2004). Teoría de la confiabilidad de sistemas: modelos, métodos estadísticos y aplicaciones . Hoboken: John Wiley & Sons. ISBN 047147133X.

Enlaces externos

Therneau, Terry. "Un paquete para el análisis de supervivencia en S". Archivado desde el original el 7 de septiembre de 2006.A través de la página del Dr. Therneau en el sitio web de Mayo Clinic
"Manual de estadística de ingeniería". NIST/SEMATEK.
SOCR , subprograma de análisis de supervivencia y actividad de aprendizaje interactiva.
Análisis del tiempo de supervivencia/falla en la página del libro de texto de estadística
Análisis de supervivencia en R
Lifelines, un paquete de Python para el análisis de supervivencia
Análisis de supervivencia en la biblioteca Fortran de NAG