Regresión logística

Modelo estadístico para una variable dependiente binaria

Ejemplo de gráfico de una curva de regresión logística ajustada a los datos. La curva muestra la probabilidad estimada de aprobar un examen (variable dependiente binaria) en función de las horas de estudio (variable independiente escalar). Consulte el § Ejemplo para obtener detalles del trabajo.

En estadística , el modelo logístico (o modelo logit ) es un modelo estadístico que modela las probabilidades logarítmicas de un evento como una combinación lineal de una o más variables independientes . En el análisis de regresión , la regresión logística ^[1] (o regresión logit ) estima los parámetros de un modelo logístico (los coeficientes en las combinaciones lineales o no lineales). En la regresión logística binaria hay una única variable dependiente binaria , codificada por una variable indicadora , donde los dos valores están etiquetados como "0" y "1", mientras que las variables independientes pueden ser cada una una variable binaria (dos clases, codificadas por una variable indicadora) o una variable continua (cualquier valor real). La probabilidad correspondiente del valor etiquetado como "1" puede variar entre 0 (ciertamente el valor "0") y 1 (ciertamente el valor "1"), de ahí el etiquetado; ^[2] la función que convierte las probabilidades logarítmicas en probabilidad es la función logística , de ahí el nombre. La unidad de medida para la escala de probabilidades logarítmicas se denomina logit , de log istic unit , de ahí los nombres alternativos. Consulte § Antecedentes y § Definición para matemáticas formales, y § Ejemplo para un ejemplo resuelto.

Las variables binarias se utilizan ampliamente en estadística para modelar la probabilidad de que ocurra una determinada clase o evento, como la probabilidad de que gane un equipo, de que un paciente esté sano, etc. (ver § Aplicaciones), y el modelo logístico ha sido el modelo más comúnmente utilizado para la regresión binaria desde aproximadamente 1970. ^[3] Las variables binarias se pueden generalizar a variables categóricas cuando hay más de dos valores posibles (por ejemplo, si una imagen es de un gato, un perro, un león, etc.), y la regresión logística binaria se puede generalizar a la regresión logística multinomial . Si se ordenan las categorías múltiples , se puede utilizar la regresión logística ordinal (por ejemplo, el modelo logístico ordinal de probabilidades proporcionales ^[4] ). Ver § Extensiones para extensiones adicionales. El modelo de regresión logística en sí mismo simplemente modela la probabilidad de salida en términos de entrada y no realiza una clasificación estadística (no es un clasificador), aunque puede usarse para hacer un clasificador, por ejemplo, eligiendo un valor de corte y clasificando las entradas con probabilidad mayor que el corte como una clase, y por debajo del corte como la otra; esta es una forma común de hacer un clasificador binario .

También se pueden utilizar modelos lineales análogos para variables binarias con una función sigmoidea diferente en lugar de la función logística (para convertir la combinación lineal en una probabilidad), en particular el modelo probit ; véase § Alternativas. La característica definitoria del modelo logístico es que al aumentar una de las variables independientes se escalan multiplicativamente las probabilidades del resultado dado a una tasa constante , y cada variable independiente tiene su propio parámetro; para una variable dependiente binaria, esto generaliza la razón de probabilidades . De manera más abstracta, la función logística es el parámetro natural de la distribución de Bernoulli y, en este sentido, es la forma "más simple" de convertir un número real en una probabilidad. En particular, maximiza la entropía (minimiza la información agregada) y, en este sentido, hace la menor cantidad de suposiciones de los datos que se están modelando; véase § Entropía máxima.

Los parámetros de una regresión logística se estiman más comúnmente mediante la estimación de máxima verosimilitud (MLE). Esta no tiene una expresión de forma cerrada, a diferencia de los mínimos cuadrados lineales ; consulte § Ajuste de modelos. La regresión logística por MLE juega un papel básico similar para las respuestas binarias o categóricas al que juega la regresión lineal por mínimos cuadrados ordinarios (MCO) para las respuestas escalares : es un modelo de referencia simple y bien analizado; consulte § Comparación con la regresión lineal para una discusión. La regresión logística como modelo estadístico general fue desarrollada originalmente y popularizada principalmente por Joseph Berkson , ^[5] comenzando en Berkson (1944), donde acuñó el término "logit"; consulte § Historia.

Aplicaciones

General

La regresión logística se utiliza en varios campos, incluido el aprendizaje automático, la mayoría de los campos médicos y las ciencias sociales. Por ejemplo, el Trauma and Injury Severity Score ( TRISS ), que se usa ampliamente para predecir la mortalidad en pacientes lesionados, fue desarrollado originalmente por Boyd et al. utilizando regresión logística. ^[6] Muchas otras escalas médicas utilizadas para evaluar la gravedad de un paciente se han desarrollado utilizando regresión logística. ^{[7] [8] [9] [10]} La regresión logística se puede utilizar para predecir el riesgo de desarrollar una enfermedad determinada (por ejemplo, diabetes ; enfermedad cardíaca coronaria ), según las características observadas del paciente (edad, sexo, índice de masa corporal , resultados de varios análisis de sangre , etc.). ^{[11] [12]} Otro ejemplo podría ser predecir si un votante nepalí votará al Congreso Nepalí o al Partido Comunista de Nepal o cualquier otro partido, en función de la edad, los ingresos, el sexo, la raza, el estado de residencia, los votos en elecciones anteriores, etc. ^[13] La técnica también se puede utilizar en ingeniería , especialmente para predecir la probabilidad de fallo de un proceso, sistema o producto determinado. ^{[14] [15]} También se utiliza en aplicaciones de marketing , como la predicción de la propensión de un cliente a comprar un producto o detener una suscripción, etc. ^[16] En economía , se puede utilizar para predecir la probabilidad de que una persona acabe en la fuerza laboral, y una aplicación empresarial sería predecir la probabilidad de que un propietario incumpla con una hipoteca . Los campos aleatorios condicionales , una extensión de la regresión logística a los datos secuenciales, se utilizan en el procesamiento del lenguaje natural . Los planificadores y los ingenieros de desastres confían en estos modelos para predecir la toma de decisiones por parte de los propietarios o los ocupantes de edificios en evacuaciones de pequeña y gran escala, como incendios de edificios, incendios forestales, huracanes, entre otros. ^{[17] [18] [19]} Estos modelos ayudan en el desarrollo de planes confiables de gestión de desastres y un diseño más seguro para el entorno construido .

Aprendizaje automático supervisado

La regresión logística es un algoritmo de aprendizaje automático supervisado que se utiliza ampliamente para tareas de clasificación binaria , como identificar si un correo electrónico es spam o no y diagnosticar enfermedades evaluando la presencia o ausencia de afecciones específicas según los resultados de las pruebas del paciente. Este enfoque utiliza la función logística (o sigmoidea) para transformar una combinación lineal de características de entrada en un valor de probabilidad que oscila entre 0 y 1. Esta probabilidad indica la probabilidad de que una entrada dada corresponda a una de dos categorías predefinidas. El mecanismo esencial de la regresión logística se basa en la capacidad de la función logística para modelar la probabilidad de resultados binarios con precisión. Con su distintiva curva en forma de S, la función logística asigna de manera efectiva cualquier número de valor real a un valor dentro del intervalo de 0 a 1. Esta característica la hace particularmente adecuada para tareas de clasificación binaria, como clasificar los correos electrónicos en "spam" o "no spam". Al calcular la probabilidad de que la variable dependiente se clasifique en un grupo específico, la regresión logística proporciona un marco probabilístico que respalda la toma de decisiones informada. ^[20]

Ejemplo

Problema

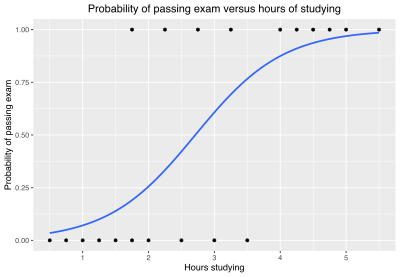
Como ejemplo simple, podemos utilizar una regresión logística con una variable explicativa y dos categorías para responder la siguiente pregunta:

Un grupo de 20 estudiantes dedica entre 0 y 6 horas a estudiar para un examen. ¿Cómo afecta el número de horas dedicadas al estudio a la probabilidad de que el estudiante apruebe el examen?

La razón para utilizar la regresión logística para este problema es que los valores de la variable dependiente, aprobado y reprobado, si bien están representados por "1" y "0", no son números cardinales . Si se cambiara el problema de modo que aprobar/reprobar se reemplazara por la calificación 0-100 (números cardinales), entonces se podría utilizar un análisis de regresión simple.

La tabla muestra el número de horas que cada estudiante dedicó al estudio y si aprobó (1) o reprobó (0).

Queremos ajustar una función logística a los datos que consisten en las horas estudiadas ( x _k ) y el resultado del examen ( y _k  = 1 para aprobado, 0 para reprobado). Los puntos de datos están indexados por el subíndice k que va de a . La variable x se llama la " variable explicativa ", y la variable y se llama la " variable categórica " ​​que consta de dos categorías: "aprobado" o "reprobado" correspondientes a los valores categóricos 1 y 0 respectivamente. ${\displaystyle k=1}$ ${\displaystyle k=K=20}$

Modelo

Gráfica de una curva de regresión logística ajustada a los datos ( x _m , y _m ). La curva muestra la probabilidad de aprobar un examen en función de las horas de estudio.

La función logística es de la forma:

${\displaystyle p(x)={\frac {1}{1+e^{-(x-\mu )/s}}}}$

donde μ es un parámetro de ubicación (el punto medio de la curva, donde ) y s es un parámetro de escala . Esta expresión puede reescribirse como: ${\displaystyle p(\mu )=1/2}$

${\displaystyle p(x)={\frac {1}{1+e^{-(\beta _{0}+\beta _{1}x)}}}}$

donde y se conoce como la intersección (es la intersección vertical o intersección con el eje y de la línea ), y (parámetro de escala inversa o parámetro de velocidad ): estos son la intersección con el eje y y la pendiente de las probabilidades logarítmicas en función de x . Por el contrario, y . ${\displaystyle \beta _{0}=-\mu /s}$ ${\displaystyle y=\beta _{0}+\beta _{1}x}$ ${\displaystyle \beta _{1}=1/s}$ ${\displaystyle \mu =-\beta _{0}/\beta _{1}}$ ${\displaystyle s=1/\beta _{1}}$

Observación: Este modelo es en realidad una simplificación excesiva, ya que supone que todos aprobarán si aprenden lo suficiente (límite = 1). El valor límite también debería ser un parámetro variable, si se desea que sea más realista.

Adaptar

La medida habitual de bondad de ajuste para una regresión logística utiliza la pérdida logística (o pérdida logarítmica ), la verosimilitud logarítmica negativa . Para unos x _k y y _k dados , escriba . Las ⁠ ⁠ son las probabilidades de que los ⁠ ⁠ correspondientes sean iguales a uno y ⁠ ⁠ son las probabilidades de que sean cero (véase la distribución de Bernoulli ). Deseamos encontrar los valores de ⁠ ⁠ y ⁠ ⁠ que den el "mejor ajuste" a los datos. En el caso de la regresión lineal, la suma de las desviaciones al cuadrado del ajuste de los puntos de datos ( y _k ), la pérdida de error al cuadrado , se toma como una medida de la bondad del ajuste, y el mejor ajuste se obtiene cuando esa función se minimiza . ${\displaystyle p_{k}=p(x_{k})}$ ${\displaystyle p_{k}}$ ${\displaystyle y_{k}}$ ${\displaystyle 1-p_{k}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{1}}$

La pérdida logarítmica para el punto k es : ${\displaystyle \ell _{k}}$

${\displaystyle \ell _{k}={\begin{cases}-\ln p_{k}&{\text{ if }}y_{k}=1,\\-\ln(1-p_{k})&{\text{ if }}y_{k}=0.\end{cases}}}$

La pérdida logarítmica puede interpretarse como la " sorpresa " del resultado real ⁠ ⁠ ${\displaystyle y_{k}}$ en relación con la predicción ⁠ ⁠ ${\displaystyle p_{k}}$ , y es una medida del contenido de información . La pérdida logarítmica siempre es mayor o igual a 0, es igual a 0 solo en el caso de una predicción perfecta (es decir, cuando y , o y ), y se acerca al infinito a medida que la predicción empeora (es decir, cuando y o y ), lo que significa que el resultado real es "más sorprendente". Dado que el valor de la función logística siempre está estrictamente entre cero y uno, la pérdida logarítmica siempre es mayor que cero y menor que infinito. A diferencia de una regresión lineal, donde el modelo puede tener pérdida cero en un punto al pasar por un punto de datos (y pérdida cero en general si todos los puntos están en una línea), en una regresión logística no es posible tener pérdida cero en ningún punto, ya que ⁠ ⁠ es 0 o 1, pero ⁠ ⁠ . ${\displaystyle p_{k}=1}$ ${\displaystyle y_{k}=1}$ ${\displaystyle p_{k}=0}$ ${\displaystyle y_{k}=0}$ ${\displaystyle y_{k}=1}$ ${\displaystyle p_{k}\to 0}$ ${\displaystyle y_{k}=0}$ ${\displaystyle p_{k}\to 1}$ ${\displaystyle y_{k}}$ ${\displaystyle 0<p_{k}<1}$

Estos se pueden combinar en una sola expresión:

${\displaystyle \ell _{k}=-y_{k}\ln p_{k}-(1-y_{k})\ln(1-p_{k}).}$

Esta expresión se conoce más formalmente como la entropía cruzada de la distribución predicha a partir de la distribución real , como distribuciones de probabilidad en el espacio de dos elementos de (aprueba, no aprueba). ${\displaystyle {\big (}p_{k},(1-p_{k}){\big )}}$ ${\displaystyle {\big (}y_{k},(1-y_{k}){\big )}}$

La suma de estos, la pérdida total, es la verosimilitud negativa general ⁠ ⁠ ${\displaystyle -\ell }$ , y el mejor ajuste se obtiene para aquellas opciones de ⁠ ⁠ ${\displaystyle \beta _{0}}$ y ⁠ ⁠ ${\displaystyle \beta _{1}}$ para las que ⁠ ⁠ ${\displaystyle -\ell }$ se minimiza .

Alternativamente, en lugar de minimizar la pérdida, se puede maximizar su inversa, la log-verosimilitud (positiva):

${\displaystyle \ell =\sum _{k:y_{k}=1}\ln(p_{k})+\sum _{k:y_{k}=0}\ln(1-p_{k})=\sum _{k=1}^{K}\left(\,y_{k}\ln(p_{k})+(1-y_{k})\ln(1-p_{k})\right)}$

o equivalentemente maximizar la función de verosimilitud en sí, que es la probabilidad de que el conjunto de datos dado sea producido por una función logística particular:

${\displaystyle L=\prod _{k:y_{k}=1}p_{k}\,\prod _{k:y_{k}=0}(1-p_{k})}$

Este método se conoce como estimación de máxima verosimilitud .

Estimación de parámetros

Dado que ℓ no es lineal en ⁠ ⁠ ${\displaystyle \beta _{0}}$ y ⁠ ⁠ ${\displaystyle \beta _{1}}$ , determinar sus valores óptimos requerirá métodos numéricos. Un método para maximizar ℓ es exigir que las derivadas de ℓ con respecto a ⁠ ⁠ ${\displaystyle \beta _{0}}$ y ⁠ ⁠ ${\displaystyle \beta _{1}}$ sean cero:

${\displaystyle 0={\frac {\partial \ell }{\partial \beta _{0}}}=\sum _{k=1}^{K}(y_{k}-p_{k})}$

${\displaystyle 0={\frac {\partial \ell }{\partial \beta _{1}}}=\sum _{k=1}^{K}(y_{k}-p_{k})x_{k}}$

y el procedimiento de maximización se puede lograr resolviendo las dos ecuaciones anteriores para ⁠ ⁠ ${\displaystyle \beta _{0}}$ y ⁠ ⁠ ${\displaystyle \beta _{1}}$ , lo que, nuevamente, generalmente requerirá el uso de métodos numéricos.

Los valores de ⁠ ⁠ ${\displaystyle \beta _{0}}$ y ⁠ ⁠ ${\displaystyle \beta _{1}}$ que maximizan ℓ y L utilizando los datos anteriores son:

${\displaystyle \beta _{0}\approx -4.1}$

${\displaystyle \beta _{1}\approx 1.5}$

lo que produce un valor para μ y s de:

${\displaystyle \mu =-\beta _{0}/\beta _{1}\approx 2.7}$

${\displaystyle s=1/\beta _{1}\approx 0.67}$

Predicciones

Los coeficientes ⁠ ⁠ ${\displaystyle \beta _{0}}$ y ⁠ ⁠ ${\displaystyle \beta _{1}}$ se pueden ingresar en la ecuación de regresión logística para estimar la probabilidad de aprobar el examen.

Por ejemplo, para un estudiante que estudia 2 horas, al introducir el valor en la ecuación se obtiene una probabilidad estimada de aprobar el examen de 0,25: ${\displaystyle x=2}$

${\displaystyle t=\beta _{0}+2\beta _{1}\approx -4.1+2\cdot 1.5=-1.1}$

${\displaystyle p={\frac {1}{1+e^{-t}}}\approx 0.25={\text{Probability of passing exam}}}$

De manera similar, para un estudiante que estudia 4 horas, la probabilidad estimada de aprobar el examen es de 0,87:

${\displaystyle t=\beta _{0}+4\beta _{1}\approx -4.1+4\cdot 1.5=1.9}$

${\displaystyle p={\frac {1}{1+e^{-t}}}\approx 0.87={\text{Probability of passing exam}}}$

Esta tabla muestra la probabilidad estimada de aprobar el examen para varios valores de horas de estudio.

Evaluación del modelo

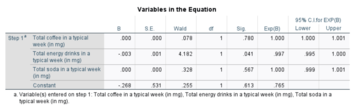
El análisis de regresión logística arroja el siguiente resultado.

Según la prueba de Wald , el resultado indica que las horas de estudio están significativamente asociadas con la probabilidad de aprobar el examen ( ). En lugar del método de Wald, el método recomendado ^[21] para calcular el valor p para la regresión logística es la prueba de razón de verosimilitud (LRT), que para estos datos arroja (ver § Pruebas de desviación y razón de verosimilitud a continuación). ${\displaystyle p=0.017}$ ${\displaystyle p\approx 0.00064}$

Generalizaciones

Este modelo simple es un ejemplo de regresión logística binaria y tiene una variable explicativa y una variable categórica binaria que puede asumir uno de dos valores categóricos. La regresión logística multinomial es la generalización de la regresión logística binaria para incluir cualquier número de variables explicativas y cualquier número de categorías.

Fondo

Figura 1. La función logística estándar ; para todos . ${\displaystyle \sigma (t)}$ ${\displaystyle \sigma (t)\in (0,1)}$ ${\displaystyle t}$

Definición de la función logística

Una explicación de la regresión logística puede comenzar con una explicación de la función logística estándar . La función logística es una función sigmoidea , que toma cualquier entrada real y genera un valor entre cero y uno. ^[2] Para el logit, esto se interpreta como tomar la entrada log-odds y tener una salida de probabilidad . La función logística estándar se define de la siguiente manera: ${\displaystyle t}$ ${\displaystyle \sigma :\mathbb {R} \rightarrow (0,1)}$

${\displaystyle \sigma (t)={\frac {e^{t}}{e^{t}+1}}={\frac {1}{1+e^{-t}}}}$

En la Figura 1 se muestra un gráfico de la función logística en el intervalo t (−6,6).

Supongamos que es una función lineal de una única variable explicativa (el caso en el que es una combinación lineal de múltiples variables explicativas se trata de manera similar). Podemos expresarlo de la siguiente manera: ${\displaystyle t}$ ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle t}$

${\displaystyle t=\beta _{0}+\beta _{1}x}$

Y la función logística general ahora se puede escribir como: ${\displaystyle p:\mathbb {R} \rightarrow (0,1)}$

${\displaystyle p(x)=\sigma (t)={\frac {1}{1+e^{-(\beta _{0}+\beta _{1}x)}}}}$

En el modelo logístico, se interpreta como la probabilidad de que la variable dependiente sea igual a un éxito/caso en lugar de un fracaso/no caso. Es evidente que las variables de respuesta no se distribuyen de forma idéntica: difieren de un punto de datos a otro, aunque son independientes dada la matriz de diseño y los parámetros compartidos . ^[11] ${\displaystyle p(x)}$ ${\displaystyle Y}$ ${\displaystyle Y_{i}}$ ${\displaystyle P(Y_{i}=1\mid X)}$ ${\displaystyle X_{i}}$ ${\displaystyle X}$ ${\displaystyle \beta }$

Definición de la inversa de la función logística

Ahora podemos definir la función logit (log odds) como la inversa de la función logística estándar. Es fácil ver que satisface: ${\displaystyle g=\sigma ^{-1}}$

${\displaystyle g(p(x))=\sigma ^{-1}(p(x))=\operatorname {logit} p(x)=\ln \left({\frac {p(x)}{1-p(x)}}\right)=\beta _{0}+\beta _{1}x,}$

y equivalentemente, después de exponenciar ambos lados tenemos las probabilidades:

${\displaystyle {\frac {p(x)}{1-p(x)}}=e^{\beta _{0}+\beta _{1}x}.}$

Interpretación de estos términos

En las ecuaciones anteriores, los términos son los siguientes:

• ${\displaystyle g}$es la función logit. La ecuación para ilustra que el logit (es decir, el logaritmo de las probabilidades o el logaritmo natural de las probabilidades) es equivalente a la expresión de regresión lineal. ${\displaystyle g(p(x))}$
• ${\displaystyle \ln }$denota el logaritmo natural .
• ${\displaystyle p(x)}$es la probabilidad de que la variable dependiente sea igual a un caso, dada alguna combinación lineal de los predictores. La fórmula para ilustra que la probabilidad de que la variable dependiente sea igual a un caso es igual al valor de la función logística de la expresión de regresión lineal. Esto es importante porque muestra que el valor de la expresión de regresión lineal puede variar de negativo a infinito positivo y, sin embargo, después de la transformación, la expresión resultante para la probabilidad varía entre 0 y 1. ${\displaystyle p(x)}$ ${\displaystyle p(x)}$
• ${\displaystyle \beta _{0}}$es la intersección de la ecuación de regresión lineal (el valor del criterio cuando el predictor es igual a cero).
• ${\displaystyle \beta _{1}x}$es el coeficiente de regresión multiplicado por algún valor del predictor.
• base denota la función exponencial. ${\displaystyle e}$

Definición de las probabilidades

La probabilidad de que la variable dependiente sea igual a un caso (dada alguna combinación lineal de los predictores) es equivalente a la función exponencial de la expresión de regresión lineal. Esto ilustra cómo el logit sirve como una función de enlace entre la probabilidad y la expresión de regresión lineal. Dado que el logit varía entre el infinito negativo y el positivo, proporciona un criterio adecuado sobre el cual realizar la regresión lineal y el logit se convierte fácilmente de nuevo en probabilidades. ^[2] ${\displaystyle x}$

Así, definimos las probabilidades de que la variable dependiente sea igual a un caso (dada una combinación lineal de los predictores) de la siguiente manera: ${\displaystyle x}$

${\displaystyle {\text{odds}}=e^{\beta _{0}+\beta _{1}x}.}$

La razón de probabilidades

Para una variable independiente continua, la razón de probabilidades se puede definir como:

La imagen representa un esquema de cómo se ve un odds ratio en la escritura, a través de una plantilla además del ejemplo de la puntuación del examen en la sección "Ejemplo" del contenido. En términos simples, si hipotéticamente obtenemos un odds ratio de 2 a 1, podemos decir... "Por cada aumento de una unidad en las horas estudiadas, las probabilidades de aprobar (grupo 1) o suspender (grupo 0) son (esperadamente) de 2 a 1 (Denis, 2019).

${\displaystyle \mathrm {OR} ={\frac {\operatorname {odds} (x+1)}{\operatorname {odds} (x)}}={\frac {\left({\frac {p(x+1)}{1-p(x+1)}}\right)}{\left({\frac {p(x)}{1-p(x)}}\right)}}={\frac {e^{\beta _{0}+\beta _{1}(x+1)}}{e^{\beta _{0}+\beta _{1}x}}}=e^{\beta _{1}}}$

Esta relación exponencial proporciona una interpretación para : Las probabilidades se multiplican por cada aumento de 1 unidad en x. ^[22] ${\displaystyle \beta _{1}}$ ${\displaystyle e^{\beta _{1}}}$

Para una variable independiente binaria, la razón de probabilidades se define como donde a , b , c y d son celdas en una tabla de contingencia de 2×2 . ^[23] ${\displaystyle {\frac {ad}{bc}}}$

Variables explicativas múltiples

Si hay múltiples variables explicativas, la expresión anterior se puede revisar a . Luego, cuando se utiliza en la ecuación que relaciona las probabilidades logarítmicas de éxito con los valores de los predictores, la regresión lineal será una regresión múltiple con m explicadores; los parámetros para todos son estimados. ${\displaystyle \beta _{0}+\beta _{1}x}$ ${\displaystyle \beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots +\beta _{m}x_{m}=\beta _{0}+\sum _{i=1}^{m}\beta _{i}x_{i}}$ ${\displaystyle \beta _{i}}$ ${\displaystyle i=0,1,2,\dots ,m}$

Nuevamente, las ecuaciones más tradicionales son:

${\displaystyle \log {\frac {p}{1-p}}=\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots +\beta _{m}x_{m}}$

y

${\displaystyle p={\frac {1}{1+b^{-(\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots +\beta _{m}x_{m})}}}}$

donde usualmente . ${\displaystyle b=e}$

Definición

Un conjunto de datos contiene N puntos. Cada punto i consta de un conjunto de m variables de entrada x _{1, i} ... x _{m, i} (también llamadas variables independientes , variables explicativas, variables predictoras, características o atributos) y una variable de resultado binaria Y _i (también conocida como variable dependiente , variable de respuesta, variable de salida o clase), es decir, puede asumir solo los dos valores posibles 0 (que a menudo significa "no" o "fracaso") o 1 (que a menudo significa "sí" o "éxito"). El objetivo de la regresión logística es utilizar el conjunto de datos para crear un modelo predictivo de la variable de resultado.

Al igual que en la regresión lineal, se supone que las variables de resultado Y _i dependen de las variables explicativas x _{1, i} ... x _m,i .

Variables explicativas

Las variables explicativas pueden ser de cualquier tipo : reales , binarias , categóricas , etc. La principal distinción es entre variables continuas y variables discretas .

(Las variables discretas que hacen referencia a más de dos opciones posibles normalmente se codifican utilizando variables ficticias (o variables indicadoras ), es decir, se crean variables explicativas separadas que toman el valor 0 o 1 para cada valor posible de la variable discreta, donde 1 significa "la variable tiene el valor dado" y 0 significa "la variable no tiene ese valor").

Variables de resultado

Formalmente, los resultados Y _i se describen como datos distribuidos según Bernoulli , donde cada resultado está determinado por una probabilidad no observada p _i que es específica del resultado en cuestión, pero relacionada con las variables explicativas. Esto se puede expresar en cualquiera de las siguientes formas equivalentes:

${\displaystyle {\begin{aligned}Y_{i}\mid x_{1,i},\ldots ,x_{m,i}\ &\sim \operatorname {Bernoulli} (p_{i})\\[5pt]\operatorname {\mathbb {E} } [Y_{i}\mid x_{1,i},\ldots ,x_{m,i}]&=p_{i}\\[5pt]\Pr(Y_{i}=y\mid x_{1,i},\ldots ,x_{m,i})&={\begin{cases}p_{i}&{\text{if }}y=1\\1-p_{i}&{\text{if }}y=0\end{cases}}\\[5pt]\Pr(Y_{i}=y\mid x_{1,i},\ldots ,x_{m,i})&=p_{i}^{y}(1-p_{i})^{(1-y)}\end{aligned}}}$

Los significados de estas cuatro líneas son:

1. La primera línea expresa la distribución de probabilidad de cada Y _i  : condicionada a las variables explicativas, sigue una distribución de Bernoulli con parámetros p _i , la probabilidad del resultado 1 para el ensayo i . Como se señaló anteriormente, cada ensayo por separado tiene su propia probabilidad de éxito, al igual que cada ensayo tiene sus propias variables explicativas. La probabilidad de éxito p _i no se observa, solo el resultado de un ensayo de Bernoulli individual que utiliza esa probabilidad.
2. La segunda línea expresa el hecho de que el valor esperado de cada Y _i es igual a la probabilidad de éxito p _i , que es una propiedad general de la distribución de Bernoulli. En otras palabras, si realizamos una gran cantidad de ensayos de Bernoulli utilizando la misma probabilidad de éxito p _i , y luego tomamos el promedio de todos los resultados 1 y 0, entonces el resultado sería cercano a p _i . Esto se debe a que al hacer un promedio de esta manera simplemente se calcula la proporción de éxitos observados, que esperamos que converjan a la probabilidad subyacente de éxito.
3. La tercera línea escribe la función de masa de probabilidad de la distribución de Bernoulli, especificando la probabilidad de ver cada uno de los dos resultados posibles.
4. La cuarta línea es otra forma de escribir la función de masa de probabilidad, que evita tener que escribir casos separados y es más conveniente para ciertos tipos de cálculos. Esto se basa en el hecho de que Y _i puede tomar solo el valor 0 o 1. En cada caso, uno de los exponentes será 1, "eligiendo" el valor debajo de él, mientras que el otro es 0, "cancelando" el valor debajo de él. Por lo tanto, el resultado es p _i o 1 −  p _i , como en la línea anterior.

Función predictora lineal

La idea básica de la regresión logística es utilizar el mecanismo ya desarrollado para la regresión lineal mediante la modelización de la probabilidad p _i utilizando una función predictora lineal , es decir, una combinación lineal de las variables explicativas y un conjunto de coeficientes de regresión que son específicos del modelo en cuestión pero los mismos para todos los ensayos. La función predictora lineal para un punto de datos particular i se escribe como: ${\displaystyle f(i)}$

${\displaystyle f(i)=\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{m}x_{m,i},}$

donde son coeficientes de regresión que indican el efecto relativo de una variable explicativa particular sobre el resultado. ${\displaystyle \beta _{0},\ldots ,\beta _{m}}$

El modelo suele presentarse de forma más compacta, como sigue:

• Los coeficientes de regresión β ₀ , β ₁ , ..., β _m se agrupan en un único vector β de tamaño m  + 1.
• Para cada punto de datos i , se añade una pseudovariable explicativa adicional x _{0, i} , con un valor fijo de 1, correspondiente al coeficiente de intersección β ₀ .
• Las variables explicativas resultantes x _{0, i} , x _{1, i} , ..., x _m,i se agrupan luego en un único vector _Xi de tamaño m  + 1.

Esto permite escribir la función predictora lineal de la siguiente manera:

${\displaystyle f(i)={\boldsymbol {\beta }}\cdot \mathbf {X} _{i},}$

utilizando la notación de un producto escalar entre dos vectores.

Este es un ejemplo de una salida de SPSS para un modelo de regresión logística que utiliza tres variables explicativas (consumo de café por semana, consumo de bebidas energéticas por semana y consumo de gaseosas por semana) y dos categorías (masculino y femenino).

Muchas variables explicativas, dos categorías

El ejemplo anterior de regresión logística binaria en una variable explicativa se puede generalizar a una regresión logística binaria en cualquier número de variables explicativas x ₁ , x ₂ ,... y cualquier número de valores categóricos . ${\displaystyle y=0,1,2,\dots }$

Para empezar, podemos considerar un modelo logístico con M variables explicativas, x ₁ , x ₂ ... x _M y, como en el ejemplo anterior, dos valores categóricos ( y = 0 y 1). Para el modelo de regresión logística binaria simple, asumimos una relación lineal entre la variable predictora y las probabilidades logarítmicas (también llamadas logit ) del evento que . Esta relación lineal puede extenderse al caso de M variables explicativas: ${\displaystyle y=1}$

${\displaystyle t=\log _{b}{\frac {p}{1-p}}=\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}+\cdots +\beta _{M}x_{M}}$

donde t es el logaritmo de las probabilidades y son los parámetros del modelo. Se ha introducido una generalización adicional en la que la base del modelo ( b ) no está restringida al número de Euler e . En la mayoría de las aplicaciones, la base del logaritmo se suele tomar como e . Sin embargo, en algunos casos puede ser más fácil comunicar los resultados trabajando en base 2 o base 10. ${\displaystyle \beta _{i}}$ ${\displaystyle b}$

Para una notación más compacta, especificaremos las variables explicativas y los coeficientes β como vectores ⁠ -dimensionales : ${\displaystyle (M+1)}$

${\displaystyle {\boldsymbol {x}}=\{x_{0},x_{1},x_{2},\dots ,x_{M}\}}$

${\displaystyle {\boldsymbol {\beta }}=\{\beta _{0},\beta _{1},\beta _{2},\dots ,\beta _{M}\}}$

con una variable explicativa añadida x ₀ = 1. El logit ahora puede escribirse como:

${\displaystyle t=\sum _{m=0}^{M}\beta _{m}x_{m}={\boldsymbol {\beta }}\cdot x}$

Resolviendo la probabilidad p obtenemos : ${\displaystyle y=1}$

${\displaystyle p({\boldsymbol {x}})={\frac {b^{{\boldsymbol {\beta }}\cdot {\boldsymbol {x}}}}{1+b^{{\boldsymbol {\beta }}\cdot {\boldsymbol {x}}}}}={\frac {1}{1+b^{-{\boldsymbol {\beta }}\cdot {\boldsymbol {x}}}}}=S_{b}(t)}$,

donde es la función sigmoidea con base . La fórmula anterior muestra que una vez que se fijan, podemos calcular fácilmente las probabilidades logarítmicas de que para una observación dada, o la probabilidad de que para una observación dada. El caso de uso principal de un modelo logístico es recibir una observación y estimar la probabilidad de que . Los coeficientes beta óptimos se pueden encontrar nuevamente maximizando la verosimilitud logarítmica. Para las mediciones K , que se definen como el vector explicativo de la medición k -ésima, y ​​como el resultado categórico de esa medición, la verosimilitud logarítmica se puede escribir en una forma muy similar al caso simple anterior: ${\displaystyle S_{b}}$ ${\displaystyle b}$ ${\displaystyle \beta _{m}}$ ${\displaystyle y=1}$ ${\displaystyle y=1}$ ${\displaystyle {\boldsymbol {x}}}$ ${\displaystyle p({\boldsymbol {x}})}$ ${\displaystyle y=1}$ ${\displaystyle {\boldsymbol {x}}_{k}}$ ${\displaystyle y_{k}}$ ${\displaystyle M=1}$

${\displaystyle \ell =\sum _{k=1}^{K}y_{k}\log _{b}(p({\boldsymbol {x_{k}}}))+\sum _{k=1}^{K}(1-y_{k})\log _{b}(1-p({\boldsymbol {x_{k}}}))}$

Como en el ejemplo simple anterior, para encontrar los parámetros β óptimos se necesitarán métodos numéricos. Una técnica útil es igualar a cero las derivadas de la verosimilitud con respecto a cada uno de los parámetros β , lo que da como resultado un conjunto de ecuaciones que se mantendrán en el valor máximo de la verosimilitud:

${\displaystyle {\frac {\partial \ell }{\partial \beta _{m}}}=0=\sum _{k=1}^{K}y_{k}x_{mk}-\sum _{k=1}^{K}p({\boldsymbol {x}}_{k})x_{mk}}$

donde x _mk es el valor de la variable explicativa x _m de la k-ésima medición.

Consideremos un ejemplo con variables explicativas, , y coeficientes , , y que se han determinado mediante el método anterior. Para ser más concretos, el modelo es: ${\displaystyle M=2}$ ${\displaystyle b=10}$ ${\displaystyle \beta _{0}=-3}$ ${\displaystyle \beta _{1}=1}$ ${\displaystyle \beta _{2}=2}$

${\displaystyle t=\log _{10}{\frac {p}{1-p}}=-3+x_{1}+2x_{2}}$

${\displaystyle p={\frac {b^{{\boldsymbol {\beta }}\cdot {\boldsymbol {x}}}}{1+b^{{\boldsymbol {\beta }}\cdot x}}}={\frac {b^{\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}}}{1+b^{\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2}}}}={\frac {1}{1+b^{-(\beta _{0}+\beta _{1}x_{1}+\beta _{2}x_{2})}}}}$,

donde p es la probabilidad del evento que . Esto se puede interpretar de la siguiente manera: ${\displaystyle y=1}$

• ${\displaystyle \beta _{0}=-3}$es la intersección con el eje y . Son las probabilidades logarítmicas del evento que , cuando los predictores . Al exponenciar, podemos ver que cuando las probabilidades del evento que son de 1 a 1000, o . De manera similar, la probabilidad del evento que cuando se puede calcular como ${\displaystyle y=1}$ ${\displaystyle x_{1}=x_{2}=0}$ ${\displaystyle x_{1}=x_{2}=0}$ ${\displaystyle y=1}$ ${\displaystyle 10^{-3}}$ ${\displaystyle y=1}$ ${\displaystyle x_{1}=x_{2}=0}$ ${\displaystyle 1/(1000+1)=1/1001.}$
• ${\displaystyle \beta _{1}=1}$significa que al aumentar en 1, las probabilidades logarítmicas aumentan en . Por lo tanto, si aumenta en 1, las probabilidades de que aumenten en un factor de . La probabilidad de también ha aumentado, pero no ha aumentado tanto como las probabilidades. ${\displaystyle x_{1}}$ ${\displaystyle 1}$ ${\displaystyle x_{1}}$ ${\displaystyle y=1}$ ${\displaystyle 10^{1}}$ ${\displaystyle y=1}$
• ${\displaystyle \beta _{2}=2}$significa que aumentar en 1 aumenta las probabilidades logarítmicas en . Entonces, si aumenta en 1, las probabilidades que aumentan en un factor de Nótese cómo el efecto de en las probabilidades logarítmicas es el doble que el efecto de , pero el efecto en las probabilidades es 10 veces mayor. Pero el efecto en la probabilidad de no es tanto como 10 veces mayor, es solo el efecto en las probabilidades que es 10 veces mayor. ${\displaystyle x_{2}}$ ${\displaystyle 2}$ ${\displaystyle x_{2}}$ ${\displaystyle y=1}$ ${\displaystyle 10^{2}.}$ ${\displaystyle x_{2}}$ ${\displaystyle x_{1}}$ ${\displaystyle y=1}$

Regresión logística multinomial: muchas variables explicativas y muchas categorías

En los casos anteriores de dos categorías (regresión logística binomial), las categorías se indexaron con "0" y "1", y teníamos dos probabilidades: la probabilidad de que el resultado estuviera en la categoría 1 estaba dada por y la probabilidad de que el resultado estuviera en la categoría 0 estaba dada por . La suma de estas probabilidades es igual a 1, lo cual debe ser cierto, ya que "0" y "1" son las únicas categorías posibles en esta configuración. ${\displaystyle p({\boldsymbol {x}})}$ ${\displaystyle 1-p({\boldsymbol {x}})}$

En general, si tenemos variables explicativas ${\displaystyle M+1}$ (incluyendo x ₀ ) y categorías ${\displaystyle N+1}$ , necesitaremos probabilidades separadas ${\displaystyle N+1}$ , una para cada categoría, indexadas por n , que describan la probabilidad de que el resultado categórico y esté en la categoría y = n , condicional al vector de covariables x . La suma de estas probabilidades para todas las categorías debe ser igual a 1. Usando la base matemáticamente conveniente e , estas probabilidades son:

${\displaystyle p_{n}({\boldsymbol {x}})={\frac {e^{{\boldsymbol {\beta }}_{n}\cdot {\boldsymbol {x}}}}{1+\sum _{u=1}^{N}e^{{\boldsymbol {\beta }}_{u}\cdot {\boldsymbol {x}}}}}}$para ${\displaystyle n=1,2,\dots ,N}$

${\displaystyle p_{0}({\boldsymbol {x}})=1-\sum _{n=1}^{N}p_{n}({\boldsymbol {x}})={\frac {1}{1+\sum _{u=1}^{N}e^{{\boldsymbol {\beta }}_{u}\cdot {\boldsymbol {x}}}}}}$

Cada una de las probabilidades excepto tendrá su propio conjunto de coeficientes de regresión . Se puede ver que, como se requiere, la suma de todas las categorías n es 1. La selección de para ser definida en términos de las otras probabilidades es artificial. Se podría haber seleccionado cualquiera de las probabilidades para ser definida de esa manera. Este valor especial de n se denomina "índice pivote", y las probabilidades logarítmicas ( t _n ) se expresan en términos de la probabilidad pivote y se expresan nuevamente como una combinación lineal de las variables explicativas: ${\displaystyle p_{0}({\boldsymbol {x}})}$ ${\displaystyle {\boldsymbol {\beta }}_{n}}$ ${\displaystyle p_{n}({\boldsymbol {x}})}$ ${\displaystyle p_{0}({\boldsymbol {x}})}$

${\displaystyle t_{n}=\ln \left({\frac {p_{n}({\boldsymbol {x}})}{p_{0}({\boldsymbol {x}})}}\right)={\boldsymbol {\beta }}_{n}\cdot {\boldsymbol {x}}}$

Obsérvese también que para el caso simple de , se recupera el caso de dos categorías, con y . ${\displaystyle N=1}$ ${\displaystyle p({\boldsymbol {x}})=p_{1}({\boldsymbol {x}})}$ ${\displaystyle p_{0}({\boldsymbol {x}})=1-p_{1}({\boldsymbol {x}})}$

Ahora se puede calcular la probabilidad logarítmica de que un conjunto particular de K mediciones o puntos de datos se generen a partir de las probabilidades anteriores. Indexando cada medición por k , denotemos el k -ésimo conjunto de variables explicativas medidas por y sus resultados categóricos por que pueden ser iguales a cualquier número entero en [0,N]. La probabilidad logarítmica es entonces: ${\displaystyle {\boldsymbol {x}}_{k}}$ ${\displaystyle y_{k}}$

${\displaystyle \ell =\sum _{k=1}^{K}\sum _{n=0}^{N}\Delta (n,y_{k})\,\ln(p_{n}({\boldsymbol {x}}_{k}))}$

donde es una función indicadora que es igual a 1 si y _k = n y cero en caso contrario. En el caso de dos variables explicativas, esta función indicadora se definió como y _k cuando n = 1 y 1-y _k cuando n = 0. Esto era conveniente, pero no necesario. ^[24] Nuevamente, los coeficientes beta óptimos se pueden encontrar maximizando la función de log-verosimilitud generalmente utilizando métodos numéricos. Un posible método de solución es establecer las derivadas de la log-verosimilitud con respecto a cada coeficiente beta igual a cero y resolver para los coeficientes beta: ${\displaystyle \Delta (n,y_{k})}$

${\displaystyle {\frac {\partial \ell }{\partial \beta _{nm}}}=0=\sum _{k=1}^{K}\Delta (n,y_{k})x_{mk}-\sum _{k=1}^{K}p_{n}({\boldsymbol {x}}_{k})x_{mk}}$

donde es el coeficiente m -ésimo del vector y es la variable explicativa m -ésima de la medición k -ésima. Una vez que se hayan estimado los coeficientes beta a partir de los datos, podremos estimar la probabilidad de que cualquier conjunto posterior de variables explicativas dé como resultado cualquiera de las posibles categorías de resultados. ${\displaystyle \beta _{nm}}$ ${\displaystyle {\boldsymbol {\beta }}_{n}}$ ${\displaystyle x_{mk}}$

Interpretaciones

Existen varias especificaciones e interpretaciones equivalentes de la regresión logística, que se ajustan a diferentes tipos de modelos más generales y permiten diferentes generalizaciones.

Como modelo lineal generalizado

El modelo particular utilizado por la regresión logística, que la distingue de la regresión lineal estándar y de otros tipos de análisis de regresión utilizados para resultados con valores binarios , es la forma en que la probabilidad de un resultado particular se vincula a la función predictora lineal:

${\displaystyle \operatorname {logit} (\operatorname {\mathbb {E} } [Y_{i}\mid x_{1,i},\ldots ,x_{m,i}])=\operatorname {logit} (p_{i})=\ln \left({\frac {p_{i}}{1-p_{i}}}\right)=\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{m}x_{m,i}}$

Escrito utilizando la notación más compacta descrita anteriormente, esto es:

${\displaystyle \operatorname {logit} (\operatorname {\mathbb {E} } [Y_{i}\mid \mathbf {X} _{i}])=\operatorname {logit} (p_{i})=\ln \left({\frac {p_{i}}{1-p_{i}}}\right)={\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}$

Esta formulación expresa la regresión logística como un tipo de modelo lineal generalizado , que predice variables con varios tipos de distribuciones de probabilidad ajustando una función predictora lineal de la forma anterior a algún tipo de transformación arbitraria del valor esperado de la variable.

La intuición para transformar usando la función logit (el logaritmo natural de las probabilidades) se explicó anteriormente ^{[ aclaración necesaria ]} . También tiene el efecto práctico de convertir la probabilidad (que está limitada a estar entre 0 y 1) en una variable que varía en el rango , coincidiendo así con el rango potencial de la función de predicción lineal en el lado derecho de la ecuación. ${\displaystyle (-\infty ,+\infty )}$

Tanto las probabilidades p _i como los coeficientes de regresión no son observables, y los medios para determinarlos no son parte del modelo en sí. Por lo general, se determinan mediante algún tipo de procedimiento de optimización, por ejemplo, la estimación de máxima verosimilitud , que encuentra los valores que mejor se ajustan a los datos observados (es decir, que dan las predicciones más precisas para los datos ya observados), generalmente sujetos a condiciones de regularización que buscan excluir valores improbables, por ejemplo, valores extremadamente grandes para cualquiera de los coeficientes de regresión. El uso de una condición de regularización es equivalente a hacer una estimación máxima a posteriori (MAP), una extensión de la máxima verosimilitud. (La regularización se realiza más comúnmente utilizando una función de regularización al cuadrado , que es equivalente a colocar una distribución previa gaussiana de media cero en los coeficientes, pero también son posibles otros regularizadores). Independientemente de si se utiliza o no la regularización, por lo general no es posible encontrar una solución de forma cerrada; En su lugar, se debe utilizar un método numérico iterativo, como los mínimos cuadrados reponderados iterativamente (IRLS) o, más comúnmente en estos días, un método cuasi-Newton como el método L-BFGS . ^[25]

La interpretación de las estimaciones del parámetro β _j es como el efecto aditivo sobre el logaritmo de las probabilidades de un cambio unitario en la variable explicativa j . En el caso de una variable explicativa dicotómica, por ejemplo, el género es la estimación de las probabilidades de tener el resultado para, digamos, los hombres en comparación con las mujeres. ${\displaystyle e^{\beta }}$

Una fórmula equivalente utiliza la inversa de la función logit, que es la función logística , es decir:

${\displaystyle \operatorname {\mathbb {E} } [Y_{i}\mid \mathbf {X} _{i}]=p_{i}=\operatorname {logit} ^{-1}({\boldsymbol {\beta }}\cdot \mathbf {X} _{i})={\frac {1}{1+e^{-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}}$

La fórmula también se puede escribir como una distribución de probabilidad (específicamente, utilizando una función de masa de probabilidad ):

${\displaystyle \Pr(Y_{i}=y\mid \mathbf {X} _{i})={p_{i}}^{y}(1-p_{i})^{1-y}=\left({\frac {e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}{1+e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}\right)^{y}\left(1-{\frac {e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}{1+e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}\right)^{1-y}={\frac {e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}\cdot y}}{1+e^{{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}}$

Como modelo de variable latente

El modelo logístico tiene una formulación equivalente a la de un modelo de variable latente . Esta formulación es común en la teoría de modelos de elección discreta y facilita su extensión a ciertos modelos más complicados con múltiples elecciones correlacionadas, así como la comparación de la regresión logística con el modelo probit, estrechamente relacionado .

Imaginemos que, para cada ensayo i , hay una variable latente continua Y _i ^* (es decir, una variable aleatoria no observada ) que se distribuye de la siguiente manera:

${\displaystyle Y_{i}^{\ast }={\boldsymbol {\beta }}\cdot \mathbf {X} _{i}+\varepsilon _{i}\,}$

dónde

${\displaystyle \varepsilon _{i}\sim \operatorname {Logistic} (0,1)\,}$

es decir, la variable latente puede escribirse directamente en términos de la función predictora lineal y una variable de error aleatorio aditivo que se distribuye de acuerdo con una distribución logística estándar .

Entonces Y _i puede verse como un indicador de si esta variable latente es positiva:

${\displaystyle Y_{i}={\begin{cases}1&{\text{if }}Y_{i}^{\ast }>0\ {\text{ i.e. }}{-\varepsilon _{i}}<{\boldsymbol {\beta }}\cdot \mathbf {X} _{i},\\0&{\text{otherwise.}}\end{cases}}}$

La elección de modelar la variable de error específicamente con una distribución logística estándar, en lugar de una distribución logística general con la ubicación y la escala establecidas en valores arbitrarios, parece restrictiva, pero de hecho no lo es. Debe tenerse en cuenta que podemos elegir nosotros mismos los coeficientes de regresión y, muy a menudo, podemos usarlos para compensar los cambios en los parámetros de la distribución de la variable de error. Por ejemplo, una distribución logística de la variable de error con un parámetro de ubicación distinto de cero μ (que establece la media) es equivalente a una distribución con un parámetro de ubicación cero, donde μ se ha añadido al coeficiente de intersección. Ambas situaciones producen el mismo valor para Y _i ^* independientemente de la configuración de las variables explicativas. De manera similar, un parámetro de escala arbitrario s es equivalente a establecer el parámetro de escala en 1 y luego dividir todos los coeficientes de regresión por s . En el último caso, el valor resultante de Y _i ^* será menor por un factor de s que en el primer caso, para todos los conjuntos de variables explicativas, pero fundamentalmente, siempre permanecerá en el mismo lado de 0 y, por lo tanto, conducirá a la misma elección de Y _{i .}

(Esto predice que la irrelevancia del parámetro de escala puede no trasladarse a modelos más complejos donde hay más de dos opciones disponibles).

Resulta que esta formulación es exactamente equivalente a la anterior, expresada en términos del modelo lineal generalizado y sin ninguna variable latente . Esto se puede demostrar de la siguiente manera, utilizando el hecho de que la función de distribución acumulativa (CDF) de la distribución logística estándar es la función logística , que es la inversa de la función logit , es decir

${\displaystyle \Pr(\varepsilon _{i}<x)=\operatorname {logit} ^{-1}(x)}$

Entonces:

${\displaystyle {\begin{aligned}\Pr(Y_{i}=1\mid \mathbf {X} _{i})&=\Pr(Y_{i}^{\ast }>0\mid \mathbf {X} _{i})\\[5pt]&=\Pr({\boldsymbol {\beta }}\cdot \mathbf {X} _{i}+\varepsilon _{i}>0)\\[5pt]&=\Pr(\varepsilon _{i}>-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})\\[5pt]&=\Pr(\varepsilon _{i}<{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&&{\text{(because the logistic distribution is symmetric)}}\\[5pt]&=\operatorname {logit} ^{-1}({\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&\\[5pt]&=p_{i}&&{\text{(see above)}}\end{aligned}}}$

Esta formulación, que es estándar en los modelos de elección discreta , deja en claro la relación entre la regresión logística (el "modelo logit") y el modelo probit , que utiliza una variable de error distribuida de acuerdo con una distribución normal estándar en lugar de una distribución logística estándar. Tanto la distribución logística como la distribución normal son simétricas con una forma básica unimodal de "curva de campana". La única diferencia es que la distribución logística tiene colas algo más pesadas , lo que significa que es menos sensible a los datos atípicos (y, por lo tanto, algo más robusta a las especificaciones incorrectas del modelo o a los datos erróneos).

Modelo de variable latente de dos vías

Otra formulación utiliza dos variables latentes separadas:

${\displaystyle {\begin{aligned}Y_{i}^{0\ast }&={\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}+\varepsilon _{0}\,\\Y_{i}^{1\ast }&={\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}+\varepsilon _{1}\,\end{aligned}}}$

dónde

${\displaystyle {\begin{aligned}\varepsilon _{0}&\sim \operatorname {EV} _{1}(0,1)\\\varepsilon _{1}&\sim \operatorname {EV} _{1}(0,1)\end{aligned}}}$

donde EV _{1 (0,1) es una} distribución de valor extremo tipo 1 estándar : es decir

${\displaystyle \Pr(\varepsilon _{0}=x)=\Pr(\varepsilon _{1}=x)=e^{-x}e^{-e^{-x}}}$

Entonces

${\displaystyle Y_{i}={\begin{cases}1&{\text{if }}Y_{i}^{1\ast }>Y_{i}^{0\ast },\\0&{\text{otherwise.}}\end{cases}}}$

Este modelo tiene una variable latente separada y un conjunto separado de coeficientes de regresión para cada resultado posible de la variable dependiente. La razón de esta separación es que facilita la extensión de la regresión logística a variables categóricas de múltiples resultados, como en el modelo logit multinomial . En un modelo de este tipo, es natural modelar cada resultado posible utilizando un conjunto diferente de coeficientes de regresión. También es posible motivar cada una de las variables latentes separadas como la utilidad teórica asociada con la toma de la elección asociada, y así motivar la regresión logística en términos de la teoría de la utilidad . (En términos de la teoría de la utilidad, un actor racional siempre elige la opción con la mayor utilidad asociada). Este es el enfoque adoptado por los economistas al formular modelos de elección discreta , porque proporciona una base teóricamente sólida y facilita intuiciones sobre el modelo, lo que a su vez facilita la consideración de varios tipos de extensiones. (Véase el ejemplo siguiente).

La elección de la distribución de valores extremos de tipo 1 parece bastante arbitraria, pero hace que las matemáticas funcionen y puede ser posible justificar su uso a través de la teoría de la elección racional .

Resulta que este modelo es equivalente al anterior, aunque esto no parece obvio, ya que ahora hay dos conjuntos de coeficientes de regresión y variables de error, y las variables de error tienen una distribución diferente. De hecho, este modelo se reduce directamente al anterior con las siguientes sustituciones:

${\displaystyle {\boldsymbol {\beta }}={\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0}}$

${\displaystyle \varepsilon =\varepsilon _{1}-\varepsilon _{0}}$

Una intuición para esto proviene del hecho de que, dado que elegimos en función del máximo de dos valores, solo importa su diferencia, no los valores exactos, y esto efectivamente elimina un grado de libertad . Otro hecho crítico es que la diferencia de dos variables distribuidas por valores extremos de tipo 1 es una distribución logística, es decir, podemos demostrar el equivalente de la siguiente manera: ${\displaystyle \varepsilon =\varepsilon _{1}-\varepsilon _{0}\sim \operatorname {Logistic} (0,1).}$

${\displaystyle {\begin{aligned}\Pr(Y_{i}=1\mid \mathbf {X} _{i})={}&\Pr \left(Y_{i}^{1\ast }>Y_{i}^{0\ast }\mid \mathbf {X} _{i}\right)&\\[5pt]={}&\Pr \left(Y_{i}^{1\ast }-Y_{i}^{0\ast }>0\mid \mathbf {X} _{i}\right)&\\[5pt]={}&\Pr \left({\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}+\varepsilon _{1}-\left({\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}+\varepsilon _{0}\right)>0\right)&\\[5pt]={}&\Pr \left(({\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}-{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i})+(\varepsilon _{1}-\varepsilon _{0})>0\right)&\\[5pt]={}&\Pr(({\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0})\cdot \mathbf {X} _{i}+(\varepsilon _{1}-\varepsilon _{0})>0)&\\[5pt]={}&\Pr(({\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0})\cdot \mathbf {X} _{i}+\varepsilon >0)&&{\text{(substitute }}\varepsilon {\text{ as above)}}\\[5pt]={}&\Pr({\boldsymbol {\beta }}\cdot \mathbf {X} _{i}+\varepsilon >0)&&{\text{(substitute }}{\boldsymbol {\beta }}{\text{ as above)}}\\[5pt]={}&\Pr(\varepsilon >-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&&{\text{(now, same as above model)}}\\[5pt]={}&\Pr(\varepsilon <{\boldsymbol {\beta }}\cdot \mathbf {X} _{i})&\\[5pt]={}&\operatorname {logit} ^{-1}({\boldsymbol {\beta }}\cdot \mathbf {X} _{i})\\[5pt]={}&p_{i}\end{aligned}}}$

Ejemplo

Como ejemplo, considere una elección a nivel provincial donde la elección es entre un partido de centroderecha, un partido de centroizquierda y un partido secesionista (por ejemplo, el Parti Québécois , que quiere que Quebec se separe de Canadá ). Entonces usaríamos tres variables latentes, una para cada opción. Luego, de acuerdo con la teoría de la utilidad , podemos interpretar las variables latentes como expresión de la utilidad que resulta de hacer cada una de las opciones. También podemos interpretar los coeficientes de regresión como indicadores de la fuerza que el factor asociado (es decir, la variable explicativa) tiene para contribuir a la utilidad, o más correctamente, la cantidad en la que un cambio unitario en una variable explicativa cambia la utilidad de una opción dada. Un votante podría esperar que el partido de centroderecha reduzca los impuestos, especialmente a las personas ricas. Esto no daría ningún beneficio a las personas de bajos ingresos, es decir, ningún cambio en la utilidad (ya que generalmente no pagan impuestos); causaría un beneficio moderado (es decir, algo más de dinero o un aumento moderado de la utilidad) para las personas de ingresos medios; Esto causaría beneficios significativos para las personas de altos ingresos. Por otra parte, se podría esperar que el partido de centro-izquierda aumentara los impuestos y compensara esto con un aumento del bienestar y otras ayudas para las clases bajas y medias. Esto causaría un beneficio positivo significativo para las personas de bajos ingresos, tal vez un beneficio débil para las personas de ingresos medios y un beneficio negativo significativo para las personas de ingresos altos. Finalmente, el partido secesionista no tomaría medidas directas sobre la economía, sino que simplemente se separaría. Un votante de ingresos bajos o medios podría esperar básicamente no obtener ninguna ganancia o pérdida de utilidad clara de esto, pero un votante de ingresos altos podría esperar una utilidad negativa ya que es probable que sea dueño de empresas, que tendrán más dificultades para hacer negocios en un entorno así y probablemente perderán dinero.

Estas intuiciones pueden expresarse de la siguiente manera:

Esto demuestra claramente que

1. Es necesario que existan conjuntos separados de coeficientes de regresión para cada opción. Si se expresa en términos de utilidad, esto se puede ver muy fácilmente. Diferentes opciones tienen diferentes efectos sobre la utilidad neta; además, los efectos varían de maneras complejas que dependen de las características de cada individuo, por lo que es necesario que existan conjuntos separados de coeficientes para cada característica, no simplemente una característica adicional por opción.
2. Aunque el ingreso es una variable continua, su efecto sobre la utilidad es demasiado complejo para tratarlo como una variable única. O bien se lo debe dividir directamente en rangos, o bien se deben sumar potencias de ingreso más altas para que la regresión polinómica sobre el ingreso se realice de manera efectiva.

Como modelo "log-lineal"

Otra formulación combina la formulación de variable latente bidireccional anterior con la formulación original anterior sin variables latentes y en el proceso proporciona un vínculo a una de las formulaciones estándar del logit multinomial .

Aquí, en lugar de escribir el logit de las probabilidades p _i como un predictor lineal, separamos el predictor lineal en dos, uno para cada uno de los dos resultados:

${\displaystyle {\begin{aligned}\ln \Pr(Y_{i}=0)&={\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}-\ln Z\\\ln \Pr(Y_{i}=1)&={\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}-\ln Z\end{aligned}}}$

Se han introducido dos conjuntos separados de coeficientes de regresión, al igual que en el modelo de variable latente de dos vías, y las dos ecuaciones aparecen en una forma que escribe el logaritmo de la probabilidad asociada como un predictor lineal, con un término adicional al final. Este término, como se ve, sirve como factor de normalización que garantiza que el resultado sea una distribución. Esto se puede ver al exponenciar ambos lados: ${\displaystyle -\ln Z}$

${\displaystyle {\begin{aligned}\Pr(Y_{i}=0)&={\frac {1}{Z}}e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}\\[5pt]\Pr(Y_{i}=1)&={\frac {1}{Z}}e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}\end{aligned}}}$

De esta forma, queda claro que el propósito de Z es asegurar que la distribución resultante sobre Y _i sea de hecho una distribución de probabilidad , es decir, que sume 1. Esto significa que Z es simplemente la suma de todas las probabilidades no normalizadas y, al dividir cada probabilidad por Z , las probabilidades se " normalizan ". Es decir:

${\displaystyle Z=e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}$

y las ecuaciones resultantes son

${\displaystyle {\begin{aligned}\Pr(Y_{i}=0)&={\frac {e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}\\[5pt]\Pr(Y_{i}=1)&={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}.\end{aligned}}}$

O en general:

${\displaystyle \Pr(Y_{i}=c)={\frac {e^{{\boldsymbol {\beta }}_{c}\cdot \mathbf {X} _{i}}}{\sum _{h}e^{{\boldsymbol {\beta }}_{h}\cdot \mathbf {X} _{i}}}}}$

Esto muestra claramente cómo generalizar esta formulación a más de dos resultados, como en el logit multinomial . Esta formulación general es exactamente la función softmax como en

${\displaystyle \Pr(Y_{i}=c)=\operatorname {softmax} (c,{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i},{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i},\dots ).}$

Para demostrar que esto es equivalente al modelo anterior, el modelo anterior está sobreespecificado, en el sentido de que y no se pueden especificar de forma independiente: más bien , conocer uno determina automáticamente el otro. Como resultado, el modelo no es identificable , en el sentido de que múltiples combinaciones de β ₀ y β ₁ producirán las mismas probabilidades para todas las posibles variables explicativas. De hecho, se puede ver que agregar cualquier vector constante a ambos producirá las mismas probabilidades: ${\displaystyle \Pr(Y_{i}=0)}$ ${\displaystyle \Pr(Y_{i}=1)}$ ${\displaystyle \Pr(Y_{i}=0)+\Pr(Y_{i}=1)=1}$

${\displaystyle {\begin{aligned}\Pr(Y_{i}=1)&={\frac {e^{({\boldsymbol {\beta }}_{1}+\mathbf {C} )\cdot \mathbf {X} _{i}}}{e^{({\boldsymbol {\beta }}_{0}+\mathbf {C} )\cdot \mathbf {X} _{i}}+e^{({\boldsymbol {\beta }}_{1}+\mathbf {C} )\cdot \mathbf {X} _{i}}}}\\[5pt]&={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}e^{\mathbf {C} \cdot \mathbf {X} _{i}}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}e^{\mathbf {C} \cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}e^{\mathbf {C} \cdot \mathbf {X} _{i}}}}\\[5pt]&={\frac {e^{\mathbf {C} \cdot \mathbf {X} _{i}}e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}{e^{\mathbf {C} \cdot \mathbf {X} _{i}}(e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}})}}\\[5pt]&={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}{e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}.\end{aligned}}}$

Como resultado, podemos simplificar las cosas y restaurar la identificabilidad eligiendo un valor arbitrario para uno de los dos vectores. Elegimos establecer Entonces, ${\displaystyle {\boldsymbol {\beta }}_{0}=\mathbf {0} .}$

${\displaystyle e^{{\boldsymbol {\beta }}_{0}\cdot \mathbf {X} _{i}}=e^{\mathbf {0} \cdot \mathbf {X} _{i}}=1}$

y entonces

${\displaystyle \Pr(Y_{i}=1)={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}{1+e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}={\frac {1}{1+e^{-{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}}=p_{i}}$

lo que demuestra que esta formulación es de hecho equivalente a la formulación anterior. (Como en la formulación de variable latente bidireccional, cualquier configuración donde producirá resultados equivalentes). ${\displaystyle {\boldsymbol {\beta }}={\boldsymbol {\beta }}_{1}-{\boldsymbol {\beta }}_{0}}$

La mayoría de los tratamientos del modelo logit multinomial comienzan extendiendo la formulación "log-lineal" presentada aquí o la formulación de variable latente de dos vías presentada anteriormente, ya que ambas muestran claramente la forma en que el modelo podría extenderse a resultados multidireccionales. En general, la presentación con variables latentes es más común en econometría y ciencias políticas , donde reinan los modelos de elección discreta y la teoría de la utilidad , mientras que la formulación "log-lineal" aquí es más común en ciencias de la computación , por ejemplo, aprendizaje automático y procesamiento del lenguaje natural .

Como un perceptrón de una sola capa

El modelo tiene una formulación equivalente

${\displaystyle p_{i}={\frac {1}{1+e^{-(\beta _{0}+\beta _{1}x_{1,i}+\cdots +\beta _{k}x_{k,i})}}}.\,}$

Esta forma funcional se denomina comúnmente perceptrón de una sola capa o red neuronal artificial de una sola capa . Una red neuronal de una sola capa calcula una salida continua en lugar de una función escalonada . La derivada de p _i con respecto a X  = ( x ₁ , ..., x _k ) se calcula a partir de la forma general:

${\displaystyle y={\frac {1}{1+e^{-f(X)}}}}$

donde f ( X ) es una función analítica en X . Con esta elección, la red neuronal de una sola capa es idéntica al modelo de regresión logística. Esta función tiene una derivada continua, lo que permite utilizarla en retropropagación . Esta función también es preferida porque su derivada se calcula fácilmente:

${\displaystyle {\frac {\mathrm {d} y}{\mathrm {d} X}}=y(1-y){\frac {\mathrm {d} f}{\mathrm {d} X}}.\,}$

En términos de datos binomiales

Un modelo estrechamente relacionado supone que cada i está asociado no con un único ensayo de Bernoulli sino con n _i ensayos independientes distribuidos de forma idéntica , donde la observación Y _i es el número de éxitos observados (la suma de las variables aleatorias individuales distribuidas según Bernoulli) y, por lo tanto, sigue una distribución binomial :

${\displaystyle Y_{i}\,\sim \operatorname {Bin} (n_{i},p_{i}),{\text{ for }}i=1,\dots ,n}$

Un ejemplo de esta distribución es la fracción de semillas ( p _i ) que germinan después de plantar n _{i .}

En términos de valores esperados , este modelo se expresa de la siguiente manera:

${\displaystyle p_{i}=\operatorname {\mathbb {E} } \left[\left.{\frac {Y_{i}}{n_{i}}}\,\right|\,\mathbf {X} _{i}\right]\,,}$

de modo que

${\displaystyle \operatorname {logit} \left(\operatorname {\mathbb {E} } \left[\left.{\frac {Y_{i}}{n_{i}}}\,\right|\,\mathbf {X} _{i}\right]\right)=\operatorname {logit} (p_{i})=\ln \left({\frac {p_{i}}{1-p_{i}}}\right)={\boldsymbol {\beta }}\cdot \mathbf {X} _{i}\,,}$

O equivalentemente:

${\displaystyle \Pr(Y_{i}=y\mid \mathbf {X} _{i})={n_{i} \choose y}p_{i}^{y}(1-p_{i})^{n_{i}-y}={n_{i} \choose y}\left({\frac {1}{1+e^{-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}\right)^{y}\left(1-{\frac {1}{1+e^{-{\boldsymbol {\beta }}\cdot \mathbf {X} _{i}}}}\right)^{n_{i}-y}\,.}$

Este modelo se puede ajustar utilizando los mismos tipos de métodos que el modelo más básico mencionado anteriormente.

Ajuste del modelo

Estimación de máxima verosimilitud (EMV)

Los coeficientes de regresión se estiman generalmente utilizando la estimación de máxima verosimilitud . ^{[26] [27]} A diferencia de la regresión lineal con residuos distribuidos normalmente, no es posible encontrar una expresión de forma cerrada para los valores de los coeficientes que maximicen la función de verosimilitud, por lo que se debe utilizar un proceso iterativo; por ejemplo, el método de Newton . Este proceso comienza con una solución tentativa, la revisa ligeramente para ver si se puede mejorar y repite esta revisión hasta que no se realicen más mejoras, momento en el que se dice que el proceso ha convergido. ^[26]

En algunos casos, el modelo puede no alcanzar la convergencia. La no convergencia de un modelo indica que los coeficientes no son significativos porque el proceso iterativo no pudo encontrar soluciones apropiadas. La falta de convergencia puede ocurrir por varias razones: tener una gran proporción de predictores a casos, multicolinealidad , escasez o separación completa .

• Tener una gran proporción de variables por caso da como resultado una estadística de Wald demasiado conservadora (que se analiza más adelante) y puede conducir a una falta de convergencia. La regresión logística regularizada está específicamente diseñada para usarse en esta situación.
• La multicolinealidad se refiere a correlaciones inaceptablemente altas entre predictores. A medida que aumenta la multicolinealidad, los coeficientes permanecen imparciales, pero los errores estándar aumentan y la probabilidad de convergencia del modelo disminuye. ^[26] Para detectar la multicolinealidad entre los predictores, se puede realizar un análisis de regresión lineal con los predictores de interés con el único propósito de examinar la estadística de tolerancia ^[26] utilizada para evaluar si la multicolinealidad es inaceptablemente alta.
• La escasez de datos se refiere a la presencia de una gran proporción de celdas vacías (celdas con recuentos de cero). Los recuentos de celdas cero son particularmente problemáticos con los predictores categóricos. Con los predictores continuos, el modelo puede inferir valores para los recuentos de celdas cero, pero este no es el caso con los predictores categóricos. El modelo no convergerá con recuentos de celdas cero para los predictores categóricos porque el logaritmo natural de cero es un valor indefinido, por lo que no se puede alcanzar la solución final del modelo. Para remediar este problema, los investigadores pueden colapsar las categorías de una manera teóricamente significativa o agregar una constante a todas las celdas. ^[26]
• Otro problema numérico que puede conducir a una falta de convergencia es la separación completa, que se refiere al caso en el que los predictores predicen perfectamente el criterio: todos los casos se clasifican con precisión y la probabilidad se maximiza con coeficientes infinitos. En tales casos, se deben volver a examinar los datos, ya que puede haber algún tipo de error. ^{[2] [ Se necesita más explicación ]}
• También se pueden adoptar enfoques semiparamétricos o no paramétricos, por ejemplo, a través de métodos de verosimilitud local o de cuasi-verosimilitud no paramétrica, que evitan suposiciones de una forma paramétrica para la función de índice y son robustos a la elección de la función de enlace (por ejemplo, probit o logit). ^[28]

Mínimos cuadrados reponderados iterativamente (IRLS)

La regresión logística binaria ( o ) se puede calcular, por ejemplo, utilizando mínimos cuadrados reponderados iterativamente (IRLS), lo que equivale a maximizar la verosimilitud logarítmica de un proceso distribuido por Bernoulli utilizando el método de Newton . Si el problema se escribe en forma de matriz vectorial, con parámetros , variables explicativas y valor esperado de la distribución de Bernoulli , los parámetros se pueden encontrar utilizando el siguiente algoritmo iterativo: ${\displaystyle y=0}$ ${\displaystyle y=1}$ ${\displaystyle \mathbf {w} ^{T}=[\beta _{0},\beta _{1},\beta _{2},\ldots ]}$ ${\displaystyle \mathbf {x} (i)=[1,x_{1}(i),x_{2}(i),\ldots ]^{T}}$ ${\displaystyle \mu (i)={\frac {1}{1+e^{-\mathbf {w} ^{T}\mathbf {x} (i)}}}}$ ${\displaystyle \mathbf {w} }$

${\displaystyle \mathbf {w} _{k+1}=\left(\mathbf {X} ^{T}\mathbf {S} _{k}\mathbf {X} \right)^{-1}\mathbf {X} ^{T}\left(\mathbf {S} _{k}\mathbf {X} \mathbf {w} _{k}+\mathbf {y} -\mathbf {\boldsymbol {\mu }} _{k}\right)}$

donde es una matriz de ponderación diagonal, el vector de valores esperados, ${\displaystyle \mathbf {S} =\operatorname {diag} (\mu (i)(1-\mu (i)))}$ ${\displaystyle {\boldsymbol {\mu }}=[\mu (1),\mu (2),\ldots ]}$

${\displaystyle \mathbf {X} ={\begin{bmatrix}1&x_{1}(1)&x_{2}(1)&\ldots \\1&x_{1}(2)&x_{2}(2)&\ldots \\\vdots &\vdots &\vdots \end{bmatrix}}}$

La matriz regresora y el vector de variables de respuesta. Se pueden encontrar más detalles en la literatura. ^[29] ${\displaystyle \mathbf {y} (i)=[y(1),y(2),\ldots ]^{T}}$

Bayesiano

Comparación de la función logística con una función probit inversa escalada (es decir, la CDF de la distribución normal ), comparando con , que hace que las pendientes sean las mismas en el origen. Esto muestra las colas más pesadas de la distribución logística. ${\displaystyle \sigma (x)}$ ${\textstyle \Phi ({\sqrt {\frac {\pi }{8}}}x)}$

En un contexto de estadística bayesiana , las distribuciones previas normalmente se colocan en los coeficientes de regresión, por ejemplo, en forma de distribuciones gaussianas . No hay una distribución previa conjugada de la función de verosimilitud en la regresión logística. Cuando la inferencia bayesiana se realizó analíticamente, esto hizo que la distribución posterior fuera difícil de calcular excepto en dimensiones muy bajas. Sin embargo, ahora, el software automático como OpenBUGS , JAGS , PyMC , Stan o Turing.jl permite calcular estas distribuciones posteriores mediante simulación, por lo que la falta de conjugación no es una preocupación. Sin embargo, cuando el tamaño de la muestra o el número de parámetros es grande, la simulación bayesiana completa puede ser lenta y las personas a menudo usan métodos aproximados como los métodos bayesianos variacionales y la propagación de expectativas .

"Regla de diez"

La regla del " uno por diez ", ampliamente utilizada, establece que los modelos de regresión logística dan valores estables para las variables explicativas si se basan en un mínimo de unos 10 eventos por variable explicativa (EPV); donde evento denota los casos que pertenecen a la categoría menos frecuente en la variable dependiente. Por lo tanto, un estudio diseñado para utilizar variables explicativas para un evento (por ejemplo, infarto de miocardio ) que se espera que ocurra en una proporción de participantes en el estudio requerirá un total de participantes. Sin embargo, existe un debate considerable sobre la confiabilidad de esta regla, que se basa en estudios de simulación y carece de un respaldo teórico seguro. ^[30] Según algunos autores ^[31] la regla es demasiado conservadora en algunas circunstancias, y los autores afirman: "Si consideramos (de manera un tanto subjetiva) que una cobertura del intervalo de confianza es menor del 93 por ciento, un error de tipo I mayor del 7 por ciento o un sesgo relativo mayor del 15 por ciento son problemáticos, nuestros resultados indican que los problemas son bastante frecuentes con 2-4 EPV, poco comunes con 5-9 EPV y aún se observan con 10-16 EPV. Los peores casos de cada problema no fueron graves con 5-9 EPV y, por lo general, comparables a los de 10-16 EPV". ^[32] ${\displaystyle k}$ ${\displaystyle p}$ ${\displaystyle 10k/p}$

Otros han encontrado resultados que no son consistentes con lo anterior, utilizando diferentes criterios. Un criterio útil es si se espera que el modelo ajustado logre la misma discriminación predictiva en una nueva muestra que la que parecía lograr en la muestra de desarrollo del modelo. Para ese criterio, pueden requerirse 20 eventos por variable candidata. ^[33] Además, se puede argumentar que se necesitan 96 observaciones solo para estimar la intersección del modelo con la precisión suficiente para que el margen de error en las probabilidades predichas sea ±0,1 con un nivel de confianza de 0,95. ^[13]

Error y significancia del ajuste

Prueba de desviación y razón de verosimilitud: un caso sencillo

En cualquier procedimiento de ajuste, la adición de otro parámetro de ajuste a un modelo (por ejemplo, los parámetros beta en un modelo de regresión logística) casi siempre mejorará la capacidad del modelo para predecir los resultados medidos. Esto será así incluso si el término adicional no tiene valor predictivo, ya que el modelo simplemente se " sobreajustará " al ruido de los datos. Surge la pregunta de si la mejora obtenida con la adición de otro parámetro de ajuste es lo suficientemente significativa como para recomendar la inclusión del término adicional, o si la mejora es simplemente la que se puede esperar del sobreajuste.

En resumen, para la regresión logística se define un estadístico conocido como desviación , que es una medida del error entre el ajuste del modelo logístico y los datos de resultado. En el límite de un gran número de puntos de datos, la desviación se distribuye mediante chi-cuadrado , lo que permite implementar una prueba de chi-cuadrado para determinar la significancia de las variables explicativas.

La regresión lineal y la regresión logística tienen muchas similitudes. Por ejemplo, en la regresión lineal simple, un conjunto de K puntos de datos ( x _k , y _k ) se ajustan a una función de modelo propuesta de la forma . El ajuste se obtiene eligiendo los b parámetros que minimizan la suma de los cuadrados de los residuos (el término de error al cuadrado) para cada punto de datos: ${\displaystyle y=b_{0}+b_{1}x}$

${\displaystyle \varepsilon ^{2}=\sum _{k=1}^{K}(b_{0}+b_{1}x_{k}-y_{k})^{2}.}$

El valor mínimo que constituye el ajuste se denotará por ${\displaystyle {\hat {\varepsilon }}^{2}}$

Se puede introducir la idea de un modelo nulo , en el que se supone que la variable x no es de utilidad para predecir los resultados y _k : Los puntos de datos se ajustan a una función de modelo nulo de la forma y  =  b ₀ con un término de error al cuadrado:

${\displaystyle \varepsilon ^{2}=\sum _{k=1}^{K}(b_{0}-y_{k})^{2}.}$

El proceso de ajuste consiste en elegir un valor de b ₀ que minimice el ajuste al modelo nulo, denotado por donde el subíndice denota el modelo nulo. Se ve que el modelo nulo está optimizado por donde es la media de los valores y _k , y el optimizado es: ${\displaystyle \varepsilon ^{2}}$ ${\displaystyle \varepsilon _{\varphi }^{2}}$ ${\displaystyle \varphi }$ ${\displaystyle b_{0}={\overline {y}}}$ ${\displaystyle {\overline {y}}}$ ${\displaystyle \varepsilon _{\varphi }^{2}}$

${\displaystyle {\hat {\varepsilon }}_{\varphi }^{2}=\sum _{k=1}^{K}({\overline {y}}-y_{k})^{2}}$

que es proporcional al cuadrado de la desviación estándar de la muestra (sin corregir) de los puntos de datos y _k .

Podemos imaginar un caso en el que los puntos de datos y _k se asignan aleatoriamente a los diversos x _k y luego se ajustan utilizando el modelo propuesto. Específicamente, podemos considerar los ajustes del modelo propuesto a cada permutación de los resultados y _k . Se puede demostrar que el error optimizado de cualquiera de estos ajustes nunca será menor que el error óptimo del modelo nulo, y que la diferencia entre estos errores mínimos seguirá una distribución de chi-cuadrado , con grados de libertad iguales a los del modelo propuesto menos los del modelo nulo que, en este caso, serán . Usando la prueba de chi-cuadrado , podemos entonces estimar cuántos de estos conjuntos permutados de y _k producirán un error mínimo menor o igual al error mínimo usando el y _k original , y así podemos estimar cuán significativa es una mejora dada por la inclusión de la variable x en el modelo propuesto. ${\displaystyle 2-1=1}$

En el caso de la regresión logística, la medida de la bondad del ajuste es la función de verosimilitud L o su logaritmo, la log-verosimilitud ℓ . La función de verosimilitud L es análoga a la del caso de la regresión lineal, excepto que la verosimilitud se maximiza en lugar de minimizarse. Denotemos la log-verosimilitud maximizada del modelo propuesto por . ${\displaystyle \varepsilon ^{2}}$ ${\displaystyle {\hat {\ell }}}$

En el caso de una regresión logística binaria simple, el conjunto de K puntos de datos se ajusta en sentido probabilístico a una función de la forma:

${\displaystyle p(x)={\frac {1}{1+e^{-t}}}}$

donde ⁠ ⁠ ${\displaystyle p(x)}$ es la probabilidad de que . Las probabilidades logarítmicas se dan por: ${\displaystyle y=1}$

${\displaystyle t=\beta _{0}+\beta _{1}x}$

y la verosimilitud logarítmica es:

${\displaystyle \ell =\sum _{k=1}^{K}\left(y_{k}\ln(p(x_{k}))+(1-y_{k})\ln(1-p(x_{k}))\right)}$

Para el modelo nulo, la probabilidad viene dada por: ${\displaystyle y=1}$

${\displaystyle p_{\varphi }(x)={\frac {1}{1+e^{-t_{\varphi }}}}}$

Las probabilidades logarítmicas para el modelo nulo se dan por:

${\displaystyle t_{\varphi }=\beta _{0}}$

y la verosimilitud logarítmica es:

${\displaystyle \ell _{\varphi }=\sum _{k=1}^{K}\left(y_{k}\ln(p_{\varphi })+(1-y_{k})\ln(1-p_{\varphi })\right)}$

Dado que tenemos el máximo de L , la máxima verosimilitud logarítmica para el modelo nulo es ${\displaystyle p_{\varphi }={\overline {y}}}$

${\displaystyle {\hat {\ell }}_{\varphi }=K(\,{\overline {y}}\ln({\overline {y}})+(1-{\overline {y}})\ln(1-{\overline {y}}))}$

El óptimo es: ${\displaystyle \beta _{0}}$

${\displaystyle \beta _{0}=\ln \left({\frac {\overline {y}}{1-{\overline {y}}}}\right)}$

donde es nuevamente la media de los valores y _k . Nuevamente, podemos considerar conceptualmente el ajuste del modelo propuesto a cada permutación de y _k y se puede demostrar que la máxima verosimilitud logarítmica de estos ajustes de permutación nunca será menor que la del modelo nulo: ${\displaystyle {\overline {y}}}$

${\displaystyle {\hat {\ell }}\geq {\hat {\ell }}_{\varphi }}$

Además, como análogo al error del caso de regresión lineal, podemos definir la desviación de un ajuste de regresión logística como:

${\displaystyle D=\ln \left({\frac {{\hat {L}}^{2}}{{\hat {L}}_{\varphi }^{2}}}\right)=2({\hat {\ell }}-{\hat {\ell }}_{\varphi })}$

que siempre será positivo o cero. La razón de esta elección es que no solo la desviación es una buena medida de la bondad del ajuste, sino que también se distribuye aproximadamente mediante chi-cuadrado, y la aproximación mejora a medida que aumenta el número de puntos de datos ( K ), volviéndose exactamente distribuida mediante chi-cuadrado en el límite de un número infinito de puntos de datos. Como en el caso de la regresión lineal, podemos usar este hecho para estimar la probabilidad de que un conjunto aleatorio de puntos de datos proporcione un mejor ajuste que el ajuste obtenido por el modelo propuesto, y así tener una estimación de cuán significativamente se mejora el modelo al incluir los x _k puntos de datos en el modelo propuesto.

Para el modelo simple de puntajes de pruebas de estudiantes descrito anteriormente, el valor máximo de la verosimilitud logarítmica del modelo nulo es El valor máximo de la verosimilitud logarítmica para el modelo simple es de modo que la desviación es ${\displaystyle {\hat {\ell }}_{\varphi }=-13.8629\ldots }$ ${\displaystyle {\hat {\ell }}=-8.02988\ldots }$ ${\displaystyle D=2({\hat {\ell }}-{\hat {\ell }}_{\varphi })=11.6661\ldots }$

Utilizando la prueba de significancia de chi-cuadrado , la integral de la distribución de chi-cuadrado con un grado de libertad desde 11,6661... hasta infinito es igual a 0,00063649...

Esto significa efectivamente que se puede esperar que aproximadamente 6 de cada 10 000 ajustes a y _k aleatorios tengan un mejor ajuste (menor desviación) que el y _k dado , por lo que podemos concluir que la inclusión de la variable x y los datos en el modelo propuesto es una mejora muy significativa con respecto al modelo nulo. En otras palabras, rechazamos la hipótesis nula con confianza. ${\displaystyle 1-D\approx 99.94\%}$

Resumen de bondad de ajuste

La bondad de ajuste en los modelos de regresión lineal se mide generalmente utilizando R 2 . Dado que esto no tiene un análogo directo en la regresión logística, se pueden utilizar en su lugar varios métodos ^{[34] : cap.21,  incluido el siguiente.}

Pruebas de desviación y razón de verosimilitud

En el análisis de regresión lineal, uno se ocupa de dividir la varianza a través de los cálculos de suma de cuadrados : la varianza en el criterio se divide esencialmente en varianza explicada por los predictores y varianza residual. En el análisis de regresión logística, se utiliza la desviación en lugar de los cálculos de suma de cuadrados. ^[35] La desviación es análoga a los cálculos de suma de cuadrados en la regresión lineal ^[2] y es una medida de la falta de ajuste a los datos en un modelo de regresión logística. ^[35] Cuando se dispone de un modelo "saturado" (un modelo con un ajuste teóricamente perfecto), la desviación se calcula comparando un modelo dado con el modelo saturado. ^[2] Este cálculo proporciona la prueba de razón de verosimilitud : ^[2]

${\displaystyle D=-2\ln {\frac {\text{likelihood of the fitted model}}{\text{likelihood of the saturated model}}}.}$

En la ecuación anterior, D representa la desviación y ln representa el logaritmo natural. El logaritmo de esta razón de verosimilitud (la razón entre el modelo ajustado y el modelo saturado) producirá un valor negativo, de ahí la necesidad de un signo negativo. Se puede demostrar que D sigue una distribución aproximada de chi-cuadrado . ^[2] Los valores más pequeños indican un mejor ajuste, ya que el modelo ajustado se desvía menos del modelo saturado. Cuando se evalúa sobre una distribución de chi-cuadrado, los valores de chi-cuadrado no significativos indican muy poca varianza no explicada y, por lo tanto, un buen ajuste del modelo. Por el contrario, un valor de chi-cuadrado significativo indica que una cantidad significativa de la varianza no está explicada.

Cuando el modelo saturado no está disponible (un caso común), la desviación se calcula simplemente como −2·(log verosimilitud del modelo ajustado), y la referencia al log verosimilitud del modelo saturado se puede eliminar de todo lo que sigue sin daño.

Dos medidas de desviación son particularmente importantes en la regresión logística: desviación nula y desviación del modelo. La desviación nula representa la diferencia entre un modelo con solo la intersección (que significa "sin predictores") y el modelo saturado. La desviación del modelo representa la diferencia entre un modelo con al menos un predictor y el modelo saturado. ^[35] En este sentido, el modelo nulo proporciona una línea base sobre la cual comparar los modelos predictores. Dado que la desviación es una medida de la diferencia entre un modelo dado y el modelo saturado, los valores más pequeños indican un mejor ajuste. Por lo tanto, para evaluar la contribución de un predictor o un conjunto de predictores, se puede restar la desviación del modelo de la desviación nula y evaluar la diferencia en una distribución de chi-cuadrado con grados de libertad ^[2] iguales a la diferencia en el número de parámetros estimados. ${\displaystyle \chi _{s-p}^{2},}$

Dejar

${\displaystyle {\begin{aligned}D_{\text{null}}&=-2\ln {\frac {\text{likelihood of null model}}{\text{likelihood of the saturated model}}}\\[6pt]D_{\text{fitted}}&=-2\ln {\frac {\text{likelihood of fitted model}}{\text{likelihood of the saturated model}}}.\end{aligned}}}$

Entonces la diferencia de ambos es:

${\displaystyle {\begin{aligned}D_{\text{null}}-D_{\text{fitted}}&=-2\left(\ln {\frac {\text{likelihood of null model}}{\text{likelihood of the saturated model}}}-\ln {\frac {\text{likelihood of fitted model}}{\text{likelihood of the saturated model}}}\right)\\[6pt]&=-2\ln {\frac {\left({\dfrac {\text{likelihood of null model}}{\text{likelihood of the saturated model}}}\right)}{\left({\dfrac {\text{likelihood of fitted model}}{\text{likelihood of the saturated model}}}\right)}}\\[6pt]&=-2\ln {\frac {\text{likelihood of the null model}}{\text{likelihood of fitted model}}}.\end{aligned}}}$

Si la desviación del modelo es significativamente menor que la desviación nula, se puede concluir que el predictor o el conjunto de predictores mejoran significativamente el ajuste del modelo. Esto es análogo a la prueba F utilizada en el análisis de regresión lineal para evaluar la importancia de la predicción. ^[35]

Pseudo-R-cuadrado

En la regresión lineal, la correlación múltiple al cuadrado, R2 ^, se utiliza para evaluar la bondad del ajuste, ya que representa la proporción de varianza en el criterio que se explica por los predictores. ^[35] En el análisis de regresión logística, no hay una medida análoga acordada, pero hay varias medidas en competencia, cada una con limitaciones. ^{[35] [36]}

En esta página se examinan cuatro de los índices más utilizados y uno menos utilizado:

• Razón de verosimilitud R ² _L
• Cox y ^Snell R2 _CS
• Uñas R ² _N
• McFadden R2 ^McF_​
• Tjur R ² _T

Prueba de Hosmer-Lemeshow

La prueba de Hosmer-Lemeshow utiliza una estadística de prueba que sigue asintóticamente una distribución para evaluar si las tasas de eventos observadas coinciden o no con las tasas de eventos esperadas en subgrupos de la población del modelo. Algunos estadísticos consideran que esta prueba es obsoleta debido a su dependencia de la clasificación arbitraria de las probabilidades predichas y su potencia relativamente baja. ^[37] ${\displaystyle \chi ^{2}}$

Significancia del coeficiente

Después de ajustar el modelo, es probable que los investigadores quieran examinar la contribución de los predictores individuales. Para ello, querrán examinar los coeficientes de regresión. En la regresión lineal, los coeficientes de regresión representan el cambio en el criterio por cada cambio de unidad en el predictor. ^[35] Sin embargo, en la regresión logística, los coeficientes de regresión representan el cambio en el logit por cada cambio de unidad en el predictor. Dado que el logit no es intuitivo, es probable que los investigadores se centren en el efecto de un predictor en la función exponencial del coeficiente de regresión: la razón de probabilidades (ver definición). En la regresión lineal, la significancia de un coeficiente de regresión se evalúa calculando una prueba t . En la regresión logística, hay varias pruebas diferentes diseñadas para evaluar la significancia de un predictor individual, en particular la prueba de razón de verosimilitud y la estadística de Wald.

Prueba de razón de verosimilitud

La prueba de razón de verosimilitud analizada anteriormente para evaluar el ajuste del modelo también es el procedimiento recomendado para evaluar la contribución de los "predictores" individuales a un modelo dado. ^{[2] [26] [35]} En el caso de un modelo de predictor único, uno simplemente compara la desviación del modelo predictor con la del modelo nulo en una distribución de chi-cuadrado con un solo grado de libertad. Si el modelo predictor tiene una desviación significativamente menor (cf chi-cuadrado utilizando la diferencia en grados de libertad de los dos modelos), entonces uno puede concluir que hay una asociación significativa entre el "predictor" y el resultado. Aunque algunos paquetes estadísticos comunes (por ejemplo, SPSS) proporcionan estadísticas de prueba de razón de verosimilitud, sin esta prueba computacionalmente intensiva sería más difícil evaluar la contribución de los predictores individuales en el caso de regresión logística múltiple. ^{[ cita requerida ]} Para evaluar la contribución de los predictores individuales uno puede ingresar los predictores jerárquicamente, comparando cada nuevo modelo con el anterior para determinar la contribución de cada predictor. ^[35] Existe cierto debate entre los estadísticos sobre la idoneidad de los procedimientos denominados "paso a paso". ^{[ palabras equívocas ]} El temor es que no preserven las propiedades estadísticas nominales y resulten engañosos. ^[38]

Estadística de Wald

Como alternativa, al evaluar la contribución de los predictores individuales en un modelo dado, se puede examinar la significancia de la estadística de Wald . La estadística de Wald, análoga a la prueba t en regresión lineal, se utiliza para evaluar la significancia de los coeficientes. La estadística de Wald es la relación entre el cuadrado del coeficiente de regresión y el cuadrado del error estándar del coeficiente y se distribuye asintóticamente como una distribución de chi-cuadrado. ^[26]

${\displaystyle W_{j}={\frac {\beta _{j}^{2}}{SE_{\beta _{j}}^{2}}}}$

Aunque varios paquetes estadísticos (por ejemplo, SPSS, SAS) informan sobre la estadística de Wald para evaluar la contribución de los predictores individuales, la estadística de Wald tiene limitaciones. Cuando el coeficiente de regresión es grande, el error estándar del coeficiente de regresión también tiende a ser mayor, lo que aumenta la probabilidad de error de tipo II . La estadística de Wald también tiende a estar sesgada cuando los datos son escasos. ^[35]

Muestreo de casos y controles

Supongamos que los casos son raros. Entonces, podríamos querer muestrearlos con una frecuencia mayor que la de su prevalencia en la población. Por ejemplo, supongamos que hay una enfermedad que afecta a 1 persona de cada 10.000 y para recopilar nuestros datos necesitamos hacer un examen físico completo. Puede resultar demasiado costoso realizar miles de exámenes físicos a personas sanas para obtener datos de sólo unos pocos individuos enfermos. Por lo tanto, podemos evaluar a más individuos enfermos, tal vez todos los casos raros. Esto también es un muestreo retrospectivo, o equivalentemente se llama datos no balanceados. Como regla general, muestrear controles a una tasa de cinco veces el número de casos producirá suficientes datos de control. ^[39]

La regresión logística es única en el sentido de que puede estimarse a partir de datos no balanceados, en lugar de datos muestreados aleatoriamente, y aun así producir estimaciones correctas de los coeficientes de los efectos de cada variable independiente en el resultado. Es decir, si formamos un modelo logístico a partir de dichos datos, si el modelo es correcto en la población general, todos los parámetros son correctos excepto . Podemos corregir si conocemos la prevalencia real de la siguiente manera: ^[39] ${\displaystyle \beta _{j}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle \beta _{0}}$

${\displaystyle {\widehat {\beta }}_{0}^{*}={\widehat {\beta }}_{0}+\log {\frac {\pi }{1-\pi }}-\log {{\tilde {\pi }} \over {1-{\tilde {\pi }}}}}$

donde es la prevalencia real y es la prevalencia en la muestra. ${\displaystyle \pi }$ ${\displaystyle {\tilde {\pi }}}$

Discusión

Al igual que otras formas de análisis de regresión , la regresión logística hace uso de una o más variables predictoras que pueden ser continuas o categóricas. Sin embargo, a diferencia de la regresión lineal ordinaria, la regresión logística se utiliza para predecir variables dependientes que toman pertenencia a una de un número limitado de categorías (tratando a la variable dependiente en el caso binomial como el resultado de un ensayo de Bernoulli ) en lugar de un resultado continuo. Dada esta diferencia, se violan los supuestos de la regresión lineal. En particular, los residuos no pueden distribuirse normalmente. Además, la regresión lineal puede hacer predicciones sin sentido para una variable dependiente binaria. Lo que se necesita es una forma de convertir una variable binaria en una continua que pueda tomar cualquier valor real (negativo o positivo). Para hacer eso, la regresión logística binomial primero calcula las probabilidades de que ocurra el evento para diferentes niveles de cada variable independiente y luego toma su logaritmo para crear un criterio continuo como una versión transformada de la variable dependiente. El logaritmo de las probabilidades es el logit de la probabilidad, el logit se define de la siguiente manera: $${\displaystyle \operatorname {logit} p=\ln {\frac {p}{1-p}}\quad {\text{for }}0<p<1\,.}$$

Aunque la variable dependiente en la regresión logística es Bernoulli, el logit está en una escala sin restricciones. ^[2] La función logit es la función de enlace en este tipo de modelo lineal generalizado, es decir $${\displaystyle \operatorname {logit} \operatorname {\mathcal {E}} (Y)=\beta _{0}+\beta _{1}x}$$

Y es la variable de respuesta distribuida según Bernoulli y x es la variable predictora; los valores β son los parámetros lineales.

El logit de la probabilidad de éxito se ajusta entonces a los predictores. El valor predicho del logit se convierte de nuevo en probabilidades predichas, a través de la inversa del logaritmo natural: la función exponencial . Por lo tanto, aunque la variable dependiente observada en la regresión logística binaria es una variable 0 o 1, la regresión logística estima las probabilidades, como una variable continua, de que la variable dependiente sea un "éxito". En algunas aplicaciones, las probabilidades son todo lo que se necesita. En otras, se necesita una predicción específica de sí o no sobre si la variable dependiente es o no un "éxito"; esta predicción categórica puede basarse en las probabilidades de éxito calculadas, y las probabilidades predichas por encima de un valor de corte elegido se traducen en una predicción de éxito.

Entropía máxima

De todas las formas funcionales utilizadas para estimar las probabilidades de un resultado categórico particular que optimizan el ajuste maximizando la función de verosimilitud (por ejemplo, regresión probit , regresión de Poisson , etc.), la solución de regresión logística es única en el sentido de que es una solución de máxima entropía . ^[40] Este es un caso de una propiedad general: una familia exponencial de distribuciones maximiza la entropía, dado un valor esperado. En el caso del modelo logístico, la función logística es el parámetro natural de la distribución de Bernoulli (está en " forma canónica ", y la función logística es la función de enlace canónica), mientras que otras funciones sigmoideas son funciones de enlace no canónicas; esto subraya su elegancia matemática y facilidad de optimización. Consulte Familia exponencial § Derivación de máxima entropía para obtener más detalles.

Prueba

Para demostrarlo, utilizamos el método de los multiplicadores de Lagrange . El lagrangiano es igual a la entropía más la suma de los productos de los multiplicadores de Lagrange por varias expresiones de restricción. Se considerará el caso multinomial general, ya que la prueba no se simplifica mucho al considerar casos más simples. Igualando la derivada del lagrangiano con respecto a las diversas probabilidades a cero, se obtiene una forma funcional para esas probabilidades que corresponde a las utilizadas en la regresión logística. ^[40]

Al igual que en la sección anterior sobre regresión logística multinomial, consideraremos ⁠ ⁠ ${\displaystyle M+1}$ variables explicativas denotadas ⁠ ⁠ ${\displaystyle x_{m}}$ y que incluyen . Habrá un total de K puntos de datos, indexados por , y los puntos de datos están dados por y ⁠ ⁠ . El x _mk también se representará como un vector ⁠ ⁠ -dimensional . Habrá ⁠ ⁠ posibles valores de la variable categórica y que van desde 0 a N. ${\displaystyle x_{0}=1}$ ${\displaystyle k=\{1,2,\dots ,K\}}$ ${\displaystyle x_{mk}}$ ${\displaystyle y_{k}}$ ${\displaystyle (M+1)}$ ${\displaystyle {\boldsymbol {x}}_{k}=\{x_{0k},x_{1k},\dots ,x_{Mk}\}}$ ${\displaystyle N+1}$

Sea p _n ( x ) la probabilidad, dado el vector de variable explicativa x , de que el resultado sea . Defina cuál es la probabilidad de que para la k -ésima medición, el resultado categórico sea n . ${\displaystyle y=n}$ ${\displaystyle p_{nk}=p_{n}({\boldsymbol {x}}_{k})}$

El lagrangiano se expresará como una función de las probabilidades p _nk y se minimizará igualando a cero las derivadas del lagrangiano con respecto a estas probabilidades. Un punto importante es que las probabilidades se tratan por igual y el hecho de que sumen 1 es parte de la formulación del lagrangiano, en lugar de asumirse desde el principio.

La primera contribución al Lagrangiano es la entropía :

${\displaystyle {\mathcal {L}}_{ent}=-\sum _{k=1}^{K}\sum _{n=0}^{N}p_{nk}\ln(p_{nk})}$

La verosimilitud logarítmica es:

${\displaystyle \ell =\sum _{k=1}^{K}\sum _{n=0}^{N}\Delta (n,y_{k})\ln(p_{nk})}$

Suponiendo la función logística multinomial, se encontró que la derivada de la verosimilitud logarítmica con respecto a los coeficientes beta era:

${\displaystyle {\frac {\partial \ell }{\partial \beta _{nm}}}=\sum _{k=1}^{K}(p_{nk}x_{mk}-\Delta (n,y_{k})x_{mk})}$

Un punto muy importante aquí es que esta expresión no es (notablemente) una función explícita de los coeficientes beta. Es solo una función de las probabilidades p _nk y los datos. En lugar de ser específica para el caso logístico multinomial asumido, se toma como una declaración general de la condición en la que se maximiza la verosimilitud logarítmica y no hace referencia a la forma funcional de p _nk . Entonces, hay ( M + 1 )( N + 1 ) restricciones de ajuste y el término de restricción de ajuste en el lagrangiano es:

${\displaystyle {\mathcal {L}}_{fit}=\sum _{n=0}^{N}\sum _{m=0}^{M}\lambda _{nm}\sum _{k=1}^{K}(p_{nk}x_{mk}-\Delta (n,y_{k})x_{mk})}$

donde λ _nm son los multiplicadores de Lagrange apropiados. Existen K restricciones de normalización que pueden escribirse:

${\displaystyle \sum _{n=0}^{N}p_{nk}=1}$

de modo que el término de normalización en el Lagrangiano es:

${\displaystyle {\mathcal {L}}_{norm}=\sum _{k=1}^{K}\alpha _{k}\left(1-\sum _{n=1}^{N}p_{nk}\right)}$

donde α _k son los multiplicadores de Lagrange apropiados. El lagrangiano es entonces la suma de los tres términos anteriores:

${\displaystyle {\mathcal {L}}={\mathcal {L}}_{ent}+{\mathcal {L}}_{fit}+{\mathcal {L}}_{norm}}$

Al establecer en cero la derivada del lagrangiano con respecto a una de las probabilidades se obtiene:

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial p_{n'k'}}}=0=-\ln(p_{n'k'})-1+\sum _{m=0}^{M}(\lambda _{n'm}x_{mk'})-\alpha _{k'}}$

Usando la notación vectorial más condensada:

${\displaystyle \sum _{m=0}^{M}\lambda _{nm}x_{mk}={\boldsymbol {\lambda }}_{n}\cdot {\boldsymbol {x}}_{k}}$

y eliminando los primos de los índices n y k , y luego resolviendo, obtenemos: ${\displaystyle p_{nk}}$

${\displaystyle p_{nk}=e^{{\boldsymbol {\lambda }}_{n}\cdot {\boldsymbol {x}}_{k}}/Z_{k}}$

dónde:

${\displaystyle Z_{k}=e^{1+\alpha _{k}}}$

Imponiendo la restricción de normalización, podemos resolver Z _k y escribir las probabilidades como:

${\displaystyle p_{nk}={\frac {e^{{\boldsymbol {\lambda }}_{n}\cdot {\boldsymbol {x}}_{k}}}{\sum _{u=0}^{N}e^{{\boldsymbol {\lambda }}_{u}\cdot {\boldsymbol {x}}_{k}}}}}$

No son todos independientes. Podemos añadir cualquier vector de dimensión constante a cada uno de los sin cambiar el valor de las probabilidades, de modo que solo haya N en lugar de independientes . En la sección de regresión logística multinomial anterior, se restó de cada uno , lo que estableció el término exponencial que involucra a 1, y los coeficientes beta se dieron por . ${\displaystyle {\boldsymbol {\lambda }}_{n}}$ ${\displaystyle (M+1)}$ ${\displaystyle {\boldsymbol {\lambda }}_{n}}$ ${\displaystyle p_{nk}}$ ${\displaystyle N+1}$ ${\displaystyle {\boldsymbol {\lambda }}_{n}}$ ${\displaystyle {\boldsymbol {\lambda }}_{0}}$ ${\displaystyle {\boldsymbol {\lambda }}_{n}}$ ${\displaystyle {\boldsymbol {\lambda }}_{0}}$ ${\displaystyle {\boldsymbol {\beta }}_{n}={\boldsymbol {\lambda }}_{n}-{\boldsymbol {\lambda }}_{0}}$

Otros enfoques

En aplicaciones de aprendizaje automático donde se utiliza regresión logística para la clasificación binaria, el MLE minimiza la función de pérdida de entropía cruzada .

La regresión logística es un algoritmo de aprendizaje automático importante . El objetivo es modelar la probabilidad de que una variable aleatoria sea 0 o 1 a partir de datos experimentales. ^[41] ${\displaystyle Y}$

Consideremos una función de modelo lineal generalizada parametrizada por , ${\displaystyle \theta }$

${\displaystyle h_{\theta }(X)={\frac {1}{1+e^{-\theta ^{T}X}}}=\Pr(Y=1\mid X;\theta )}$

Por lo tanto,

${\displaystyle \Pr(Y=0\mid X;\theta )=1-h_{\theta }(X)}$

y como , vemos que está dado por Ahora calculamos la función de verosimilitud suponiendo que todas las observaciones en la muestra están distribuidas independientemente según Bernoulli, ${\displaystyle Y\in \{0,1\}}$ ${\displaystyle \Pr(y\mid X;\theta )}$ ${\displaystyle \Pr(y\mid X;\theta )=h_{\theta }(X)^{y}(1-h_{\theta }(X))^{(1-y)}.}$

${\displaystyle {\begin{aligned}L(\theta \mid y;x)&=\Pr(Y\mid X;\theta )\\&=\prod _{i}\Pr(y_{i}\mid x_{i};\theta )\\&=\prod _{i}h_{\theta }(x_{i})^{y_{i}}(1-h_{\theta }(x_{i}))^{(1-y_{i})}\end{aligned}}}$

Normalmente, se maximiza la probabilidad logarítmica.

${\displaystyle N^{-1}\log L(\theta \mid y;x)=N^{-1}\sum _{i=1}^{N}\log \Pr(y_{i}\mid x_{i};\theta )}$

que se maximiza utilizando técnicas de optimización como el descenso de gradiente .

Suponiendo que los pares se extraen uniformemente de la distribución subyacente, entonces en el límite de  N grande , ${\displaystyle (x,y)}$

${\displaystyle {\begin{aligned}&\lim \limits _{N\rightarrow +\infty }N^{-1}\sum _{i=1}^{N}\log \Pr(y_{i}\mid x_{i};\theta )=\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}\Pr(X=x,Y=y)\log \Pr(Y=y\mid X=x;\theta )\\[6pt]={}&\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}\Pr(X=x,Y=y)\left(-\log {\frac {\Pr(Y=y\mid X=x)}{\Pr(Y=y\mid X=x;\theta )}}+\log \Pr(Y=y\mid X=x)\right)\\[6pt]={}&-D_{\text{KL}}(Y\parallel Y_{\theta })-H(Y\mid X)\end{aligned}}}$

donde es la entropía condicional y es la divergencia de Kullback–Leibler . Esto lleva a la intuición de que al maximizar la verosimilitud logarítmica de un modelo, se minimiza la divergencia KL de su modelo con respecto a la distribución de entropía máxima. Búsqueda intuitiva del modelo que realiza la menor cantidad de suposiciones en sus parámetros. ${\displaystyle H(Y\mid X)}$ ${\displaystyle D_{\text{KL}}}$

Comparación con regresión lineal

La regresión logística puede considerarse un caso especial del modelo lineal generalizado y, por lo tanto, análoga a la regresión lineal . Sin embargo, el modelo de regresión logística se basa en supuestos bastante diferentes (sobre la relación entre las variables dependientes e independientes) de los de la regresión lineal. En particular, las diferencias clave entre estos dos modelos se pueden ver en las siguientes dos características de la regresión logística. En primer lugar, la distribución condicional es una distribución de Bernoulli en lugar de una distribución gaussiana , porque la variable dependiente es binaria. En segundo lugar, los valores predichos son probabilidades y, por lo tanto, están restringidos a (0,1) a través de la función de distribución logística porque la regresión logística predice la probabilidad de resultados particulares en lugar de los resultados en sí. ${\displaystyle y\mid x}$

Alternativas

Una alternativa común al modelo logístico (modelo logit) es el modelo probit , como sugieren los nombres relacionados. Desde la perspectiva de los modelos lineales generalizados , estos difieren en la elección de la función de enlace : el modelo logístico utiliza la función logit (función logística inversa), mientras que el modelo probit utiliza la función probit ( función de error inversa ). Equivalentemente, en las interpretaciones de variable latente de estos dos métodos, el primero supone una distribución logística estándar de errores y el segundo una distribución normal estándar de errores. ^[42] Se pueden utilizar otras funciones sigmoides o distribuciones de error en su lugar.

La regresión logística es una alternativa al método de Fisher de 1936, el análisis discriminante lineal . ^[43] Si se cumplen los supuestos del análisis discriminante lineal, el condicionamiento puede invertirse para producir una regresión logística. Sin embargo, lo inverso no es cierto, porque la regresión logística no requiere el supuesto normal multivariante del análisis discriminante. ^[44]

La suposición de efectos predictores lineales se puede relajar fácilmente utilizando técnicas como las funciones spline . ^[13]

Historia

En Cramer (2002) se ofrece una historia detallada de la regresión logística. La función logística fue desarrollada como un modelo de crecimiento de la población y denominada "logística" por Pierre François Verhulst en las décadas de 1830 y 1840, bajo la guía de Adolphe Quetelet ; véase Función logística § Historia para más detalles. ^[45] En su primer artículo (1838), Verhulst no especificó cómo ajustó las curvas a los datos. ^{[46] [47]} En su artículo más detallado (1845), Verhulst determinó los tres parámetros del modelo haciendo que la curva pasara por tres puntos observados, lo que produjo predicciones deficientes. ^{[48] [49]}

La función logística fue desarrollada independientemente en química como un modelo de autocatálisis ( Wilhelm Ostwald , 1883). ^[50] Una reacción autocatalítica es aquella en la que uno de los productos es en sí mismo un catalizador para la misma reacción, mientras que el suministro de uno de los reactivos es fijo. Esto naturalmente da lugar a la ecuación logística por la misma razón que el crecimiento de la población: la reacción se refuerza a sí misma pero está restringida.

La función logística fue redescubierta independientemente como un modelo de crecimiento poblacional en 1920 por Raymond Pearl y Lowell Reed , publicado como Pearl & Reed (1920), lo que llevó a su uso en las estadísticas modernas. Inicialmente desconocían el trabajo de Verhulst y presumiblemente lo aprendieron de L. Gustave du Pasquier , pero le dieron poco crédito y no adoptaron su terminología. ^[51] La prioridad de Verhulst fue reconocida y el término "logístico" revivió por Udny Yule en 1925 y se ha utilizado desde entonces. ^[52] Pearl y Reed aplicaron por primera vez el modelo a la población de los Estados Unidos, y también ajustaron inicialmente la curva haciéndola pasar por tres puntos; como con Verhulst, esto nuevamente arrojó malos resultados. ^[53]

En la década de 1930, el modelo probit fue desarrollado y sistematizado por Chester Ittner Bliss , quien acuñó el término "probit" en Bliss (1934), y por John Gaddum en Gaddum (1933), y el modelo ajustado por estimación de máxima verosimilitud por Ronald A. Fisher en Fisher (1935), como un complemento al trabajo de Bliss. El modelo probit se utilizó principalmente en bioensayos , y había sido precedido por trabajos anteriores que databan de 1860; consulte Modelo probit § Historia . El modelo probit influyó en el desarrollo posterior del modelo logit y estos modelos compitieron entre sí. ^[54]

El modelo logístico fue probablemente utilizado por primera vez como una alternativa al modelo probit en bioensayos por Edwin Bidwell Wilson y su estudiante Jane Worcester en Wilson & Worcester (1943). ^[55] Sin embargo, el desarrollo del modelo logístico como una alternativa general al modelo probit se debió principalmente al trabajo de Joseph Berkson durante muchas décadas, comenzando en Berkson (1944), donde acuñó "logit", por analogía con "probit", y continuando con Berkson (1951) y años siguientes. ^[56] El modelo logit fue inicialmente descartado como inferior al modelo probit, pero "gradualmente logró un pie de igualdad con el probit", ^[57] particularmente entre 1960 y 1970. Para 1970, el modelo logit logró la paridad con el modelo probit en uso en revistas de estadística y luego lo superó. Esta relativa popularidad se debió a la adopción del logit fuera del bioensayo, en lugar de desplazar al probit dentro del bioensayo, y a su uso informal en la práctica; la popularidad del logit se atribuye a la simplicidad computacional, las propiedades matemáticas y la generalidad del modelo logit, lo que permite su uso en diversos campos. ^[3]

Durante ese tiempo se produjeron varios refinamientos, en particular por parte de David Cox , como en Cox (1958). ^[4]

El modelo logit multinomial fue introducido independientemente en Cox (1966) y Theil (1969), lo que aumentó en gran medida el alcance de aplicación y la popularidad del modelo logit. ^[58] En 1973, Daniel McFadden vinculó el logit multinomial a la teoría de la elección discreta , específicamente al axioma de elección de Luce , mostrando que el logit multinomial se deducía del supuesto de independencia de alternativas irrelevantes e interpretando las probabilidades de las alternativas como preferencias relativas; ^[59] esto dio una base teórica para la regresión logística. ^[58]

Extensiones

Hay un gran número de extensiones:

• La regresión logística multinomial (o logit multinomial ) maneja el caso de una variable dependiente categórica de múltiples vías (con valores no ordenados, también llamada "clasificación"). El caso general de tener variables dependientes con más de dos valores se denomina regresión politómica .
• La regresión logística ordenada (o logit ordenada ) maneja variables dependientes ordinales (valores ordenados).
• El logit mixto es una extensión del logit multinomial que permite correlaciones entre las elecciones de la variable dependiente.
• Una extensión del modelo logístico a conjuntos de variables interdependientes es el campo aleatorio condicional .
• La regresión logística condicional maneja datos pareados o estratificados cuando los estratos son pequeños. Se utiliza principalmente en el análisis de estudios observacionales .

Véase también

• Portal de matemáticas

• Función logística
• Elección discreta
• Modelo de Jarrow-Turnbull
• Variable dependiente limitada
• Modelo logit multinomial
• Logit ordenado
• Prueba de Hosmer-Lemeshow
• Puntuación de Brier
• mlpack : contiene una implementación en C++ de regresión logística
• Muestreo de casos y controles locales
• Árbol modelo logístico

Referencias

1. Tolles, Juliana; Meurer, William J (2016). "Regresión logística que relaciona las características de los pacientes con los resultados". JAMA . 316 (5): 533–4. doi :10.1001/jama.2016.7653. ISSN  0098-7484. OCLC  6823603312. PMID  27483067.
2. Hosmer, David W.; Lemeshow, Stanley (2000). Regresión logística aplicada (2.ª ed.). Wiley. ISBN 978-0-471-35632-5. ^{[ página necesaria ]}
3. Cramer 2002, págs. 10-11.
4. Walker, SH; Duncan, DB (1967). "Estimación de la probabilidad de un evento como función de varias variables independientes". Biometrika . 54 (1/2): 167–178. doi :10.2307/2333860. JSTOR  2333860.
5. Cramer 2002, pág. 8.
6. Boyd, CR; Tolson, MA; Copes, WS (1987). "Evaluación de la atención de trauma: el método TRISS. Puntuación de trauma y puntuación de gravedad de la lesión". The Journal of Trauma . 27 (4): 370–378. doi : 10.1097/00005373-198704000-00005 . PMID  3106646.
7. Kologlu, M.; Elker, D.; Altun, H.; Sayek, I. (2001). "Validación de MPI y PIA II en dos grupos diferentes de pacientes con peritonitis secundaria". Hepato-Gastroenterology . 48 (37): 147–51. PMID  11268952.
8. Biondo, S.; Ramos, E.; Deiros, M.; Ragué, JM; De Oca, J.; Moreno, P.; Farrán, L.; Jaurrieta, E. (2000). "Factores pronósticos de mortalidad en peritonitis del colon izquierdo: un nuevo sistema de puntuación". Revista del Colegio Americano de Cirujanos . 191 (6): 635–42. doi :10.1016/S1072-7515(00)00758-4. PMID  11129812.
9. Marshall, JC; Cook, DJ; Christou, NV; Bernard, GR; Sprung, CL; Sibbald, WJ (1995). "Puntuación de disfunción orgánica múltiple: un descriptor fiable de un resultado clínico complejo". Medicina de cuidados críticos . 23 (10): 1638–52. doi :10.1097/00003246-199510000-00007. PMID  7587228.
10. Le Gall, JR; Lemeshow, S.; Saulnier, F. (1993). "Una nueva escala simplificada de fisiología aguda (SAPS II) basada en un estudio multicéntrico europeo/norteamericano". JAMA . 270 (24): 2957–63. doi :10.1001/jama.1993.03510240069035. PMID  8254858.
11. David A. Freedman (2009). Modelos estadísticos: teoría y práctica . Cambridge University Press . pág. 128.
12. Truett, J; Cornfield, J; Kannel, W (1967). "Un análisis multivariado del riesgo de enfermedad cardíaca coronaria en Framingham". Revista de enfermedades crónicas . 20 (7): 511–24. doi :10.1016/0021-9681(67)90082-3. PMID  6028270.
13. Harrell, Frank E. (2015). Estrategias de modelado de regresión . Springer Series in Statistics (2.ª ed.). Nueva York; Springer. doi :10.1007/978-3-319-19425-7. ISBN 978-3-319-19424-0.
14. M. Strano; BM Colosimo (2006). "Análisis de regresión logística para la determinación experimental de diagramas de límite de conformado". Revista internacional de máquinas herramientas y fabricación . 46 (6): 673–682. doi :10.1016/j.ijmachtools.2005.07.005.
15. Palei, SK; Das, SK (2009). "Modelo de regresión logística para la predicción de riesgos de caída de techos en trabajos con pilares y tablones en minas de carbón: un enfoque". Safety Science . 47 : 88–96. doi :10.1016/j.ssci.2008.01.002.
16. Berry, Michael JA (1997). Técnicas de minería de datos para marketing, ventas y atención al cliente . Wiley. pág. 10.
17. Mesa-Arango, Rodrigo; Hasan, Samiul; Ukkusuri, Satish V.; Murray-Tuite, Pamela (febrero de 2013). "Modelo a nivel de hogar para la elección del tipo de destino de evacuación en caso de huracán utilizando datos del huracán Iván". Natural Hazards Review . 14 (1): 11–20. doi :10.1061/(ASCE)NH.1527-6996.0000083. ISSN  1527-6988.
18. Wibbenmeyer, Matthew J.; Hand, Michael S.; Calkin, David E.; Venn, Tyron J.; Thompson, Matthew P. (junio de 2013). "Preferencias de riesgo en la toma de decisiones estratégicas sobre incendios forestales: un experimento de elección con gestores de incendios forestales de EE. UU." Análisis de riesgos . 33 (6): 1021–1037. Bibcode :2013RiskA..33.1021W. doi :10.1111/j.1539-6924.2012.01894.x. ISSN  0272-4332. PMID  23078036. S2CID  45282555.
19. Lovreglio, Ruggiero; Borri, Dino; dell'Olio, Luigi; Ibeas, Angel (1 de febrero de 2014). "Un modelo de elección discreta basado en utilidades aleatorias para la elección de salida en evacuaciones de emergencia". Safety Science . 62 : 418–426. doi :10.1016/j.ssci.2013.10.004. ISSN  0925-7535.
20. "Regresión logística". CORP-MIDS1 (MDS) . Consultado el 16 de marzo de 2024 .
21. Neyman, J. ; Pearson, ES (1933), "Sobre el problema de las pruebas más eficientes de hipótesis estadísticas" (PDF) , Philosophical Transactions of the Royal Society of London A , 231 (694–706): 289–337, Bibcode :1933RSPTA.231..289N, doi : 10.1098/rsta.1933.0009 , JSTOR  91247
22. "¿Cómo interpretar la razón de probabilidades en la regresión logística?". Instituto de Investigación y Educación Digital.
23. Everitt, Brian (1998). Diccionario de estadística de Cambridge . Cambridge, Reino Unido. Nueva York: Cambridge University Press. ISBN 978-0-521-59346-5.
24. Por ejemplo, la función indicadora en este caso podría definirse como ${\displaystyle \Delta (n,y)=1-(y-n)^{2}}$
25. Malouf, Robert (2002). "Una comparación de algoritmos para la estimación de parámetros de máxima entropía". Actas de la Sexta Conferencia sobre Aprendizaje de Lenguas Naturales (CoNLL-2002) . págs. 49–55. doi : 10.3115/1118853.1118871 .
26. Menard, Scott W. (2002). Regresión logística aplicada (2.ª ed.). SAGE. ISBN 978-0-7619-2208-7. ^{[ página necesaria ]}
27. Gourieroux, Christian; Monfort, Alain (1981). "Propiedades asintóticas del estimador de máxima verosimilitud en modelos logit dicotómicos". Journal of Econometrics . 17 (1): 83–97. doi :10.1016/0304-4076(81)90060-9.
28. Park, Byeong U.; Simar, Léopold; Zelenyuk, Valentin (2017). "Estimación no paramétrica de modelos dinámicos de elección discreta para datos de series temporales" (PDF) . Computational Statistics & Data Analysis . 108 : 97–120. doi :10.1016/j.csda.2016.10.024.
29. Murphy, Kevin P. (2012). Aprendizaje automático: una perspectiva probabilística . The MIT Press. pág. 245. ISBN 978-0-262-01802-9.
30. Van Smeden, M.; De Groot, JA; Moons, KG; Collins, GS; Altman, DG; Eijkemans, MJ; Reitsma, JB (2016). "No hay fundamento para el criterio de 1 variable por cada 10 eventos para el análisis de regresión logística binaria". Metodología de investigación médica de BMC . 16 (1): 163. doi : 10.1186/s12874-016-0267-3 . PMC 5122171 . PMID  27881078. 
31. Peduzzi, P; Concato, J; Kemper, E; Holford, TR; Feinstein, AR (diciembre de 1996). "Un estudio de simulación del número de eventos por variable en el análisis de regresión logística". Journal of Clinical Epidemiology . 49 (12): 1373–9. doi : 10.1016/s0895-4356(96)00236-3 . PMID  8970487.
32. Vittinghoff, E.; McCulloch, CE (12 de enero de 2007). "Relajación de la regla de diez eventos por variable en regresión logística y de Cox". American Journal of Epidemiology . 165 (6): 710–718. doi : 10.1093/aje/kwk052 . PMID  17182981.
33. van der Ploeg, Tjeerd; Austin, Peter C.; Steyerberg, Ewout W. (2014). "Las técnicas de modelado modernas consumen muchos datos: un estudio de simulación para predecir puntos finales dicotómicos". BMC Medical Research Methodology . 14 : 137. doi : 10.1186/1471-2288-14-137 . PMC 4289553 . PMID  25532820. 
34. Greene, William N. (2003). Análisis econométrico (quinta edición). Prentice-Hall. ISBN 978-0-13-066189-0.
35. Cohen, Jacob; Cohen, Patricia; West, Steven G.; Aiken, Leona S. (2002). Análisis de correlación/regresión múltiple aplicado a las ciencias del comportamiento (3.ª ed.). Routledge. ISBN 978-0-8058-2223-6. ^{[ página necesaria ]}
36. Allison, Paul D. "Medidas de ajuste para la regresión logística" (PDF) . Statistical Horizons LLC y la Universidad de Pensilvania.
37. Hosmer, DW (1997). "Una comparación de pruebas de bondad de ajuste para el modelo de regresión logística". Stat Med . 16 (9): 965–980. doi :10.1002/(sici)1097-0258(19970515)16:9<965::aid-sim509>3.3.co;2-f. PMID  9160492.
38. Harrell, Frank E. (2010). Estrategias de modelado de regresión: con aplicaciones a modelos lineales, regresión logística y análisis de supervivencia . Nueva York: Springer. ISBN 978-1-4419-2918-1.^{[ página necesaria ]}
39. https://class.stanford.edu/c4x/HumanitiesScience/StatLearning/asset/classification.pdf diapositiva 16
40. Mount, J. (2011). "La equivalencia de los modelos de regresión logística y máxima entropía" (PDF) . Consultado el 23 de febrero de 2022 .
41. Ng, Andrew (2000). "CS229 Apuntes de clase" (PDF) . CS229 Apuntes de clase : 16–19.
42. Rodríguez, G. (2007). Apuntes sobre modelos lineales generalizados. pp. Capítulo 3, página 45.
43. Gareth James; Daniela Witten; Trevor Hastie; Robert Tibshirani (2013). Introducción al aprendizaje estadístico. Springer. pág. 6.
44. Pohar, Maja; Blas, Mateja; Turco, Sandra (2004). "Comparación de regresión logística y análisis discriminante lineal: un estudio de simulación". Metodološki Zvezki . 1 (1).
45. Cramer 2002, págs. 3-5.
46. Verhulst, Pierre-François (1838). "Aviso sobre la ley que la población poursuit dans son accroissement" (PDF) . Correspondencia Mathématique et Physique . 10 : 113–121 . Consultado el 3 de diciembre de 2014 .
47. Cramer 2002, p. 4, "No dijo cómo ajustó las curvas".
48. Verhulst, Pierre-François (1845). "Recherches mathématiques sur la loi d'accroissement de la populación" [Investigaciones matemáticas sobre la ley del crecimiento demográfico]. Nuevas memorias de la Academia Real de Ciencias y Bellas Letras de Bruselas . 18 . Consultado el 18 de febrero de 2013 .
49. Cramer 2002, pág. 4.
50. Cramer 2002, pág. 7.
51. Cramer 2002, pág. 6.
52. Cramer 2002, págs. 6–7.
53. Cramer 2002, pág. 5.
54. Cramer 2002, págs. 7–9.
55. Cramer 2002, pág. 9.
56. Cramer 2002, p. 8, "Hasta donde puedo ver, la introducción de la logística como alternativa a la función de probabilidad normal es obra de una sola persona, Joseph Berkson (1899-1982), ..."
57. Cramer 2002, pág. 11.
58. Cramer 2002, pág. 13.
59. McFadden, Daniel (1973). "Conditional Logit Analysis of Qualitative Choice Behavior" (PDF) . En P. Zarembka (ed.). Frontiers in Econometrics . Nueva York: Academic Press. pp. 105–142. Archivado desde el original (PDF) el 2018-11-27 . Consultado el 20 de abril de 2019 .

Fuentes

• Berkson, Joseph (1944). "Aplicación de la función logística al bioensayo". Revista de la Asociación Estadounidense de Estadística . 39 (227): 357–365. doi :10.1080/01621459.1944.10500699. JSTOR  2280041.
• Berkson, Joseph (1951). "Por qué prefiero los logits a los probits". Biometrics . 7 (4): 327–339. doi :10.2307/3001655. ISSN  0006-341X. JSTOR  3001655.
• Bliss, CI (1934). "El método de los probits". Science . 79 (2037): 38–39. Bibcode :1934Sci....79...38B. doi :10.1126/science.79.2037.38. PMID  17813446. Estas unidades de probabilidad arbitrarias se han denominado "probits".
• Cox, David R. (1958). "El análisis de regresión de secuencias binarias (con discusión)". JR Stat Soc B . 20 (2): 215–242. doi :10.1111/j.2517-6161.1958.tb00292.x. JSTOR  2983890.
• Cox, David R. (1966). "Algunos procedimientos relacionados con la curva de respuesta cualitativa logística". En FN David (ed.). Artículos de investigación en probabilidad y estadística (Festschrift for J. Neyman) . Londres: Wiley. págs. 55–71.
• Cramer, JS (2002). Los orígenes de la regresión logística (PDF) (Informe técnico). Vol. 119. Tinbergen Institute. págs. 167–178. doi :10.2139/ssrn.360300.
  • Publicado en: Cramer, JS (2004). "Los orígenes tempranos del modelo logit". Estudios de Historia y Filosofía de la Ciencia Parte C: Estudios de Historia y Filosofía de las Ciencias Biológicas y Biomédicas . 35 (4): 613–626. doi :10.1016/j.shpsc.2004.09.003.
• Fisher, RA (1935). "El caso de cero supervivientes en ensayos probit". Annals of Applied Biology . 22 : 164–165. doi :10.1111/j.1744-7348.1935.tb07713.x. Archivado desde el original el 30 de abril de 2014.
• Gaddum, John H. (1933). Informes sobre estándares biológicos: métodos de ensayo biológico que dependen de una respuesta cuántica. III . HM Stationery Office. OCLC  808240121.
• Theil, Henri (1969). "Una extensión multinomial del modelo logit lineal". Revista Económica Internacional . 10 (3): 251–59. doi :10.2307/2525642. JSTOR  2525642.
• Pearl, Raymond; Reed, Lowell J. (junio de 1920). "Sobre la tasa de crecimiento de la población de los Estados Unidos desde 1790 y su representación matemática". Actas de la Academia Nacional de Ciencias . 6 (6): 275–288. Bibcode :1920PNAS....6..275P. doi : 10.1073/pnas.6.6.275 . PMC  1084522 . PMID  16576496.
• Wilson, EB ; Worcester, J. (1943). "La determinación de LD50 y su error de muestreo en bioensayo". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 29 (2): 79–85. Bibcode :1943PNAS...29...79W. doi : 10.1073/pnas.29.2.79 . PMC  1078563 . PMID  16588606.

• Agresti, Alan. (2002). Análisis de datos categóricos . Nueva York: Wiley-Interscience. ISBN 978-0-471-36093-3.
• Amemiya, Takeshi (1985). "Modelos de respuesta cualitativa". Econometría avanzada . Oxford: Basil Blackwell. pp. 267–359. ISBN 978-0-631-13345-2.
• Balakrishnan, N. (1991). Manual de distribución logística . Marcel Dekker, Inc. ISBN 978-0-8247-8587-1.
• Gouriéroux, Christian (2000). "La dicotomía simple". Econometría de variables dependientes cualitativas . Nueva York: Cambridge University Press. pp. 6–37. ISBN 978-0-521-58985-7.
• Greene, William H. (2003). Análisis econométrico, quinta edición . Prentice Hall. ISBN 978-0-13-066189-0.
• Hilbe, Joseph M. (2009). Modelos de regresión logística . Chapman & Hall/CRC Press. ISBN 978-1-4200-7575-5.
• Hosmer, David (2013). Regresión logística aplicada . Hoboken, Nueva Jersey: Wiley. ISBN 978-0-470-58247-3.
• Howell, David C. (2010). Métodos estadísticos para la psicología, 7.ª ed . Belmont, CA; Thomson Wadsworth. ISBN 978-0-495-59786-5.
• Peduzzi, P.; J. Concato; E. Kemper; TR Holford; AR Feinstein (1996). "Un estudio de simulación del número de eventos por variable en el análisis de regresión logística". Journal of Clinical Epidemiology . 49 (12): 1373–1379. doi : 10.1016/s0895-4356(96)00236-3 . PMID  8970487.
• Berry, Michael JA; Linoff, Gordon (1997). Técnicas de minería de datos para marketing, ventas y atención al cliente . Wiley.

Enlaces externos

• Medios relacionados con Regresión logística en Wikimedia Commons
• Conferencia sobre econometría (tema: modelo logit) en YouTube por Mark Thoma
• Tutorial de regresión logística
• mlelr: software en C para fines didácticos