Reflexión interna total

En física , la reflexión interna total ( TIR ) es el fenómeno en el que las ondas que llegan a la interfaz (límite) de un medio a otro (por ejemplo, del agua al aire) no se refractan en el segundo medio ("externo"), sino que se reflejan completamente de vuelta en el primer medio ("interno"). Ocurre cuando el segundo medio tiene una velocidad de onda más alta (es decir, un índice de refracción más bajo ) que el primero, y las ondas inciden en un ángulo suficientemente oblicuo en la interfaz. Por ejemplo, la superficie del agua al aire en una pecera típica, cuando se ve oblicuamente desde abajo, refleja la escena submarina como un espejo sin pérdida de brillo (Fig. 1).

La TIR se produce no sólo con ondas electromagnéticas como la luz y las microondas , sino también con otros tipos de ondas, incluidas las ondas sonoras y las ondas de agua . Si las ondas son capaces de formar un haz estrecho (Fig. 2), la reflexión tiende a describirse en términos de " rayos " en lugar de ondas; en un medio cuyas propiedades son independientes de la dirección, como el aire, el agua o el vidrio , los "rayos" son perpendiculares a los frentes de onda asociados . La reflexión interna total se produce cuando se supera el ángulo crítico.

La refracción generalmente va acompañada de una reflexión parcial . Cuando las ondas se refractan desde un medio de menor velocidad de propagación (mayor índice de refracción ) a un medio de mayor velocidad de propagación (menor índice de refracción), por ejemplo, del agua al aire, el ángulo de refracción (entre el rayo saliente y la normal a la superficie ) es mayor que el ángulo de incidencia (entre el rayo entrante y la normal). A medida que el ángulo de incidencia se acerca a un cierto umbral, llamado ángulo crítico , el ángulo de refracción se acerca a 90°, en el que el rayo refractado se vuelve paralelo a la superficie límite. A medida que el ángulo de incidencia aumenta más allá del ángulo crítico, las condiciones de refracción ya no se pueden satisfacer, por lo que no hay rayo refractado y la reflexión parcial se vuelve total. Para la luz visible , el ángulo crítico es de aproximadamente 49° para la incidencia del agua al aire y de aproximadamente 42° para la incidencia del vidrio común al aire.

Los detalles del mecanismo de la TIR dan lugar a fenómenos más sutiles. Mientras que la reflexión total, por definición, no implica un flujo continuo de energía a través de la interfaz entre los dos medios, el medio externo transporta una denominada onda evanescente , que viaja a lo largo de la interfaz con una amplitud que disminuye exponencialmente con la distancia desde la interfaz. La reflexión "total" es de hecho total si el medio externo no tiene pérdidas (es perfectamente transparente), es continua y de extensión infinita, pero puede ser notablemente menor que la total si la onda evanescente es absorbida por un medio externo con pérdidas (" reflectancia total atenuada "), o desviada por el límite exterior del medio externo o por objetos incrustados en ese medio ("TIR frustrada"). A diferencia de la reflexión parcial entre medios transparentes, la reflexión interna total está acompañada por un cambio de fase no trivial (no solo cero o 180°) para cada componente de polarización (perpendicular o paralelo al plano de incidencia ), y los cambios varían con el ángulo de incidencia. La explicación de este efecto por Augustin-Jean Fresnel , en 1823, aumentó la evidencia a favor de la teoría ondulatoria de la luz .

Los cambios de fase se utilizan en el invento de Fresnel, el rombo de Fresnel , para modificar la polarización. La eficiencia de la reflexión interna total se aprovecha en fibras ópticas (utilizadas en cables de telecomunicaciones y en fibroscopios formadores de imágenes ) y en prismas reflectantes , como los prismas de techo o Porro para la formación de imágenes en monoculares y binoculares .

Descripción óptica

Aunque la reflexión interna total puede ocurrir con cualquier tipo de onda que pueda decirse que tiene incidencia oblicua, incluidas (por ejemplo) las microondas ^[1] y las ondas sonoras ^[2] , es más común en el caso de las ondas de luz .

La reflexión interna total de la luz se puede demostrar utilizando un bloque cilíndrico semicircular de vidrio común o vidrio acrílico . En la Fig. 3, una "caja de rayos" proyecta un haz estrecho de luz (un " rayo ") radialmente hacia adentro. La sección transversal semicircular del vidrio permite que el rayo entrante permanezca perpendicular a la parte curva de la superficie de aire/vidrio y, por lo tanto, continúe en línea recta hacia la parte plana de la superficie, aunque su ángulo con la parte plana varía.

En el lugar donde el rayo se encuentra con la interfaz plana vidrio-aire, el ángulo entre el rayo y la normal (perpendicular) a la interfaz se denomina ángulo de incidencia . ^[3] Si este ángulo es suficientemente pequeño, el rayo se refleja parcialmente pero se transmite en su mayor parte, y la porción transmitida se refracta alejándose de la normal, de modo que el ángulo de refracción (entre el rayo refractado y la normal a la interfaz) es mayor que el ángulo de incidencia. Por el momento, llamemos al ángulo de incidencia θ _i y al ángulo de refracción θ _t (donde t es para transmitido , reservando r para reflejado ). A medida que θ _i aumenta y se acerca a un cierto "ángulo crítico", denotado por θ _c (o a veces θ _cr ), el ángulo de refracción se acerca a 90° (es decir, el rayo refractado se acerca a una tangente a la interfaz), y el rayo refractado se vuelve más débil mientras que el rayo reflejado se vuelve más brillante. ^[4] A medida que θ _i aumenta más allá de θ _c , el rayo refractado desaparece y solo queda el rayo reflejado, de modo que toda la energía del rayo incidente se refleja; esto es la reflexión interna total (TIR). En resumen:

Si θ _i < θ _c ‍ , ‍ el rayo incidente se divide, siendo en parte reflejado y en parte refractado;
Si θ _i > θ _c ‍ , ‍ el rayo incidente sufre reflexión interna total (TIR); nada de él se transmite.

Angulo critico

El ángulo crítico es el ángulo de incidencia más pequeño que produce una reflexión total, o equivalentemente el ángulo más grande para el cual existe un rayo refractado. ^[5] Para las ondas de luz incidentes desde un medio "interno" con un índice de refracción único $n 1$ , ‍ a un medio "externo" con un índice de refracción único $n 2$ , ‍ el ángulo crítico está dado por ‍ y se define si $‍ n$ $2$ $\leq$ $n$ $1$ . Para algunos otros tipos de ondas, es más conveniente pensar en términos de velocidades de propagación en lugar de índices de refracción. La explicación del ángulo crítico en términos de velocidades es más general y, por lo tanto, se discutirá primero. $\theta _{{\text{c}}\!}=\arcsin(n_{2}/n_{1})\,,$

Cuando un frente de onda se refracta de un medio a otro, las porciones incidente (entrante) y refractada (saliente) del frente de onda se encuentran en una línea común en la superficie refractante (interfaz). Sea esta línea, denotada por L , la que se mueve a una velocidad $u$ a través de la superficie, ^[6]^[7] donde $u$ se mide normal a L ‍ ( Fig. 4). Sea que los frentes de onda incidente y refractado se propaguen con velocidades normales y (respectivamente), y sea que formen los ángulos diedros θ ₁ y θ ₂ (respectivamente) con la interfaz. A partir de la geometría, ‍ es el componente de $u$ en la dirección normal a la onda incidente, de modo que ‍ De manera similar , ‍ Resolviendo cada ecuación para $1/$ $u$ e igualando los resultados, obtenemos la ley general de refracción para ondas: $estilo de visualización v_{1}$ $estilo de visualización v_{2}$ $estilo de visualización v_{1}$ $v_{1\!}=u\sin \theta _ {1}\,.$ $v_{2}=u\sin \theta _ {2}\,.$

Pero el ángulo diedro entre dos planos es también el ángulo entre sus normales. Por lo tanto, θ ₁ es el ángulo entre la normal al frente de onda incidente y la normal a la interfaz, mientras que θ ₂ es el ángulo entre la normal al frente de onda refractado y la normal a la interfaz; y la ecuación ( 1 ) nos dice que los senos de estos ángulos están en la misma proporción que las velocidades respectivas. ^[8]

Este resultado tiene la forma de la " ley de Snell ", excepto que todavía no hemos dicho que la relación de velocidades es constante, ni identificado θ ₁ y θ ₂ con los ángulos de incidencia y refracción (llamados θ _i y θ _t anteriormente). Sin embargo, si ahora suponemos que las propiedades de los medios son isótropas (independientes de la dirección), se siguen dos conclusiones adicionales: primero, las dos velocidades, y por lo tanto su relación, son independientes de sus direcciones; y segundo, las direcciones normales de onda coinciden con las direcciones de los rayos , de modo que θ ₁ y θ ₂ coinciden con los ángulos de incidencia y refracción como se definieron anteriormente. ^{[Nota 1]}

Obviamente, el ángulo de refracción no puede superar los 90°. En el caso límite, ponemos $θ$ $2$ $= 90°$ y $θ$ $1$ $=$ $θ$ $c$ en la ecuación ( 1 ), y calculamos el ángulo crítico:

Para derivar este resultado, mantenemos el supuesto de medios isotrópicos para identificar θ ₁ y θ ₂ con los ángulos de incidencia y refracción. ^{[Nota 3]}

Para las ondas electromagnéticas , y especialmente para la luz, es habitual expresar los resultados anteriores en términos de índices de refracción . El índice de refracción de un medio con velocidad normal se define como ‍ donde c es la velocidad de la luz en el vacío. ^[9] Por lo tanto ‍ De manera similar , ‍ Haciendo estas sustituciones en las ecuaciones ( 1 ) y ( 2 ), obtenemos $v_{1}$ $n_{1\!}=c/v_{1}\,,$ $v_{1\!}=c/n_{1}\,.$ $v_{2}=c/n_{2}\,.$

La ecuación ( 3 ) es la ley de refracción para medios generales, en términos de índices de refracción, siempre que θ ₁ y θ ₂ se tomen como los ángulos diedros; pero si los medios son isótropos , entonces $n 1$ y $n 2$ se vuelven independientes de la dirección mientras que θ ₁ y θ ₂ pueden tomarse como los ángulos de incidencia y refracción para los rayos, y se sigue la ecuación ( 4 ). Por lo tanto, para medios isótropos, las ecuaciones ( 3 ) y ( 4 ) juntas describen el comportamiento en la figura 5.

Según la ecuación ( 4 ), para la incidencia del agua ( $n 1 \approx 1,333$ ) al aire ( $n 2 \approx 1$ ), tenemos $θ$ $c$ $\approx 48,6°$ , mientras que para la incidencia del vidrio común o acrílico ( $n$ $1$ $\approx 1,50$ ) al aire ( $n$ $2$ $\approx 1$ ), tenemos $θ$ $c$ $\approx 41,8°$ .

La función arcoseno que produce θ _c se define solo si $n$ $2$ $\leq$ $n$ $1$ Por lo tanto, para medios isótropos, no puede ocurrir reflexión interna total si el segundo medio tiene un índice de refracción más alto (velocidad normal más baja) que el primero. Por ejemplo, no puede haber TIR para la incidencia del aire al agua; en cambio, el ángulo crítico para la incidencia del agua al aire es el ángulo de refracción en incidencia rasante del aire al agua (Fig. 6). ^[10] $(v_{2}\geq v_{1})\,.$

El medio con el índice de refracción más alto se describe comúnmente como ópticamente más denso , y el que tiene el índice de refracción más bajo como ópticamente más raro . ^[11] Por lo tanto, se dice que la reflexión interna total es posible para la incidencia "densa a rara", pero no para la incidencia "rara a densa".

Ejemplos cotidianos

Si nos situamos junto a un acuario con los ojos por debajo del nivel del agua, es probable que veamos peces u objetos sumergidos reflejados en la superficie del agua y el aire (fig. 1). El brillo de la imagen reflejada (tan brillante como la vista "directa") puede ser sorprendente.

Un efecto similar se puede observar al abrir los ojos mientras se nada justo debajo de la superficie del agua. Si el agua está en calma, la superficie fuera del ángulo crítico (medido desde la vertical) aparece como un espejo, reflejando los objetos que están debajo. La región sobre el agua no se puede ver excepto desde arriba, donde el campo de visión hemisférico se comprime en un campo cónico conocido como ventana de Snell , cuyo diámetro angular es el doble del ángulo crítico (cf. Fig. 6). ^[12] El campo de visión sobre el agua es teóricamente de 180° de ancho, pero parece menor porque a medida que miramos más cerca del horizonte, la dimensión vertical se comprime más fuertemente por la refracción; por ejemplo, por la ecuación. ( 3 ), para ángulos de incidencia aire-agua de 90°, 80° y 70°, los ángulos de refracción correspondientes son 48,6° ( θ _cr en la Fig. 6), 47,6° y 44,8°, lo que indica que la imagen de un punto a 20° por encima del horizonte está a 3,8° del borde de la ventana de Snell, mientras que la imagen de un punto a 10° por encima del horizonte está a solo 1° del borde. ^[13]

La figura 7, por ejemplo, es una fotografía tomada cerca del fondo de la parte menos profunda de una piscina. Lo que parece una amplia franja horizontal en la pared de la derecha consiste en los bordes inferiores de una fila de azulejos naranjas y sus reflejos; esto marca el nivel del agua, que luego se puede rastrear a lo largo de la otra pared. La nadadora ha alterado la superficie sobre ella, alterando la mitad inferior de su reflejo y distorsionando el reflejo de la escalera (a la derecha). Pero la mayor parte de la superficie aún está en calma, lo que da un reflejo claro del fondo de azulejos de la piscina. El espacio sobre el agua no es visible excepto en la parte superior del marco, donde las manijas de la escalera son apenas discernibles sobre el borde de la ventana de Snell, dentro de la cual el reflejo del fondo de la piscina es solo parcial, pero aún perceptible en la fotografía. Incluso se puede discernir la franja de color del borde de la ventana de Snell, debido a la variación del índice de refracción, por lo tanto del ángulo crítico, con la longitud de onda (ver Dispersión ).

Fig. 8 : Un diamante redondo de talla "brillante"

El ángulo crítico influye en los ángulos en los que se cortan las piedras preciosas . El corte redondo " brillante ", por ejemplo, está diseñado para refractar la luz incidente en las facetas frontales, reflejarla dos veces por TIR en las facetas posteriores y transmitirla nuevamente a través de las facetas frontales, de modo que la piedra se vea brillante. El diamante (Fig. 8) es especialmente adecuado para este tratamiento, porque su alto índice de refracción (aproximadamente 2,42) y, en consecuencia, su pequeño ángulo crítico (aproximadamente 24,5°) producen el comportamiento deseado en una amplia gama de ángulos de visión. ^[14] Los materiales más baratos que son igualmente susceptibles a este tratamiento incluyen la circonia cúbica (índice ≈ 2,15) y la moissanita (no isotrópica, por lo tanto doblemente refractiva , con un índice que varía de aproximadamente 2,65 a 2,69, ^{[Nota 4]} dependiendo de la dirección y la polarización); ambos son, por lo tanto, populares como simuladores de diamantes .

Onda evanescente

Matemáticamente, las ondas se describen en términos de campos que varían con el tiempo , siendo un "campo" una función de la ubicación en el espacio. Una onda que se propaga requiere un campo de "esfuerzo" y un campo de "flujo", siendo este último un vector (si trabajamos en dos o tres dimensiones). El producto del esfuerzo y el flujo está relacionado con la potencia (véase Equivalencia de sistemas ). Por ejemplo, para las ondas sonoras en un fluido no viscoso , podríamos tomar el campo de esfuerzo como la presión (un escalar) y el campo de flujo como la velocidad del fluido (un vector). El producto de estos dos es la intensidad (potencia por unidad de área). ^[15]^{[Nota 5]} Para las ondas electromagnéticas, tomaremos el campo de esfuerzo como el campo eléctrico $E y$ el campo de flujo como el campo magnetizante $H.$ Ambos son vectores, y su producto vectorial es nuevamente la intensidad (véase el vector de Poynting ). ^[16]

Cuando una onda en (por ejemplo) el medio 1 se refleja en la interfaz entre el medio 1 y el medio 2, el campo de flujo en el medio 1 es la suma vectorial de los campos de flujo debido a las ondas incidente y reflejada. ^{[Nota 6]} Si la reflexión es oblicua, los campos incidente y reflejado no están en direcciones opuestas y, por lo tanto, no pueden cancelarse en la interfaz; incluso si la reflexión es total, el componente normal o el componente tangencial del campo combinado (como una función de la ubicación y el tiempo) deben ser distintos de cero adyacentes a la interfaz. Además, las leyes físicas que gobiernan los campos generalmente implicarán que uno de los dos componentes es continuo a través de la interfaz (es decir, no cambia repentinamente cuando cruzamos la interfaz); por ejemplo, para las ondas electromagnéticas, una de las condiciones de la interfaz es que el componente tangencial de $H$ es continuo si no hay corriente superficial. ^[17] Por lo tanto, incluso si la reflexión es total, debe haber alguna penetración del campo de flujo en el medio 2; y esto, en combinación con las leyes que relacionan los campos de esfuerzo y flujo, implica que también habrá alguna penetración del campo de esfuerzo. La misma condición de continuidad implica que la variación ("ondulación") del campo en el medio 2 estará sincronizada con la de las ondas incidentes y reflejadas en el medio 1.

Pero, si la reflexión es total, la penetración espacial de los campos en el medio 2 debe limitarse de alguna manera, o de lo contrario la extensión total y, por lo tanto, la energía total de esos campos continuarían aumentando, drenando energía del medio 1. La reflexión total de un tren de ondas continuo permite que se almacene algo de energía en el medio 2, pero no permite una transferencia continua de energía del medio 1 al medio 2.

Así, utilizando un razonamiento principalmente cualitativo, podemos concluir que la reflexión interna total debe estar acompañada de un campo ondulatorio en el medio "externo", que viaja a lo largo de la interfaz en sincronismo con las ondas incidente y reflejada, pero con algún tipo de penetración espacial limitada en el medio "externo"; un campo de este tipo puede llamarse una onda evanescente .

La figura 9 muestra la idea básica. Se supone que la onda incidente es plana y sinusoidal . Para simplificar, no se muestra la onda reflejada. La onda evanescente viaja hacia la derecha en sincronía con las ondas incidente y reflejada, pero su amplitud disminuye a medida que aumenta la distancia desde la interfaz.

(Más adelante se explicarán dos características de la onda evanescente de la figura 9: primero, que las crestas de la onda evanescente son perpendiculares a la interfaz; y segundo, que la onda evanescente está ligeramente por delante de la onda incidente).

Reflexión interna total frustrada (FTIR)

Para que la reflexión interna sea total, no debe haber desviación de la onda evanescente. Supongamos, por ejemplo, que las ondas electromagnéticas incidentes desde el vidrio (con un índice de refracción más alto) al aire (con un índice de refracción más bajo) en un cierto ángulo de incidencia están sujetas a TIR. Y supongamos que tenemos un tercer medio (a menudo idéntico al primero) cuyo índice de refracción es suficientemente alto como para que, si el tercer medio reemplazara al segundo, obtendríamos un tren de ondas transmitido estándar para el mismo ángulo de incidencia. Entonces, si el tercer medio se lleva a una distancia de algunas longitudes de onda de la superficie del primer medio, donde la onda evanescente tiene una amplitud significativa en el segundo medio, entonces la onda evanescente se refracta efectivamente en el tercer medio, dando una transmisión distinta de cero en el tercer medio y, por lo tanto, una reflexión menor que la total en el primer medio. ^[18] A medida que la amplitud de la onda evanescente decae a través del espacio de aire, las ondas transmitidas se atenúan , de modo que hay menos transmisión y, por lo tanto, más reflexión, de la que habría sin espacio; pero mientras haya alguna transmisión, la reflexión es menor que la total. Este fenómeno se denomina reflexión interna total frustrada (donde "frustrada" niega "total"), abreviada como "TIR frustrada" o "FTIR".

La TIR frustrada se puede observar mirando la parte superior de un vaso de agua sostenido en la mano (Fig. 10). Si el vaso se sostiene con más fuerza, el contacto puede no ser lo suficientemente cercano y amplio como para producir un efecto perceptible. Pero si se sostiene con más fuerza, las crestas de las huellas dactilares interactúan fuertemente con las ondas evanescentes, lo que permite ver las crestas a través de la superficie de vidrio y aire, que de otro modo sería totalmente reflectante. ^[19]

El mismo efecto se puede demostrar con microondas, utilizando parafina como medio "interno" (donde existen las ondas incidentes y reflejadas). En este caso, el ancho de la abertura permitida podría ser (por ejemplo) 1 cm o varios cm, lo que es fácilmente observable y ajustable. ^[1]^[20]

El término TIR frustrado también se aplica al caso en el que la onda evanescente es dispersada por un objeto suficientemente cercano a la interfaz reflectante. Este efecto, junto con la fuerte dependencia de la cantidad de luz dispersada con respecto a la distancia desde la interfaz, se aprovecha en la microscopía de reflexión interna total . ^[21]

El mecanismo de FTIR se llama acoplamiento de ondas evanescentes y es un buen análogo para visualizar el efecto túnel cuántico . ^[22] Debido a la naturaleza ondulatoria de la materia, un electrón tiene una probabilidad distinta de cero de "hacer un túnel" a través de una barrera, incluso si la mecánica clásica diría que su energía es insuficiente. ^[18]^[19] De manera similar, debido a la naturaleza ondulatoria de la luz, un fotón tiene una probabilidad distinta de cero de cruzar un espacio, incluso si la óptica de rayos diría que su aproximación es demasiado oblicua.

Otra razón por la que la reflexión interna puede ser menor que la total, incluso más allá del ángulo crítico, es que el medio externo puede ser "permeable" (menos que perfectamente transparente), en cuyo caso el medio externo absorberá energía de la onda evanescente, de modo que el mantenimiento de la onda evanescente extraerá energía de la onda incidente. La reflexión menor que la total resultante se denomina reflectancia total atenuada (ATR). Este efecto, y especialmente la dependencia de la frecuencia de la absorción, se puede utilizar para estudiar la composición de un medio externo desconocido. ^[23]

Derivación de onda evanescente

En una onda electromagnética sinusoidal plana uniforme, el campo eléctrico $E$ tiene la forma

donde $E k$ es el vector de amplitud complejo (constante) , $i$ es la unidad imaginaria , $k$ es el vector de onda (cuya magnitud $k$ es el número de onda angular ), $r$ es el vector de posición , ω es la frecuencia angular , $t$ es el tiempo, y se entiende que la parte real de la expresión es el campo físico. ^{[Nota 7]} El campo magnetizante $H$ tiene la misma forma con los mismos $k$ y ω . El valor de la expresión no cambia si la posición $r$ varía en una dirección normal a $k$ ; por lo tanto, $k$ es normal a los frentes de onda .

Si ℓ es el componente de $r$ en la dirección de $k ‍ ,$ ‍ el campo ( 5 ) puede escribirse Si el argumento de debe ser constante, ℓ debe aumentar a la velocidad ‍ conocida como velocidad de fase . ^[24] Esto a su vez es igual a donde $c$ es la velocidad de fase en el medio de referencia (tomado como vacío) y $n$ es el índice de refracción local con respecto al medio de referencia. Resolviendo para $k$ se obtiene ‍ es decir $\mathbf {E_{k}} e^{i(k\ell -\omega t)}\,.$ $e^{i(\cdots )}$ $\omega /k\,,\,$ $c/n\,,\,$ $k=n\omega /c\,,\,$

donde es el número de onda en el vacío. ^[25]^{[Nota 8]} $\,k_{0}=\omega /c\,$

De ( 5 ), el campo eléctrico en el medio "externo" tiene la forma

donde $k t$ es el vector de onda para la onda transmitida (asumimos medios isotrópicos, pero aún no asumimos que la onda transmitida sea evanescente).

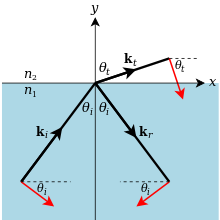
En coordenadas cartesianas $(x, y, ‍ z)$ , sea la región $‍ y$ $< 0$ ‍ con índice de refracción $n$ $1$ $‍ ,$ ‍ y sea la región $‍ y$ $> 0$ ‍ con índice de refracción $n$ $2$ . Entonces el plano $xz es la interfaz, y el eje$ $y$ es normal a la interfaz (Fig. 11). Sean $i$ y $j$ (en letra romana en negrita ) los vectores unitarios en las direcciones $x$ e $y$ , respectivamente. Sea el plano de incidencia (que contiene la normal a la onda incidente y la normal a la interfaz) el plano $xy$ (el plano de la página), con el ángulo de incidencia θ _i medido desde $j$ hacia $i$ . Sea el ángulo de refracción, medido en el mismo sentido, θ _t ( t para transmitida , reservando r para reflejada ).

De ( 6 ), el vector de onda transmitido $k t$ tiene magnitud $n 2 k 0$ . Por lo tanto, de la geometría, donde el último paso utiliza la ley de Snell. Tomando el producto escalar con el vector de posición, obtenemos que la ecuación ( 7 ) se convierte en $\mathbf {k} _{\text{t}}=n_{2}k_{0}(\mathbf {i} \sin \theta _{\text{t}}+\mathbf {j} \cos \theta _{\text{t}})=k_{0}(\mathbf {i} \,n_{1}\sin \theta _{\text{i}}+\mathbf {j} \,n_{2}\cos \theta _{\text{t}})\,,$ $\mathbf {k} _{\text{t}}\mathbf {\cdot r} =k_{0}(n_{1}x\sin \theta _{\text{i}}+n_{2}y\cos \theta _{\text{t}})\,,$

En el caso de TIR, el ángulo θ _t no existe en el sentido habitual. Pero aún podemos interpretar ( 8 ) para la onda transmitida (evanescente), permitiendo que $cos θ t$ sea complejo . Esto se hace necesario cuando escribimos $cos θ t$ en términos de $sen θ t ‍ ,$ ‍ y, por lo tanto, en términos de $sen θ i$ utilizando la ley de Snell: Para θ _i mayor que el ángulo crítico, el valor bajo el símbolo de raíz cuadrada es negativo, de modo que ^[26] $\cos \theta _{\text{t}}={\sqrt {1-\sin ^{2}\theta _{\text{t}}}}={\sqrt {1-(n_{1}/n_{2})^{2}\sin ^{2}\theta _{\text{i}}}}\,.$

Para determinar qué signo es aplicable, sustituimos ( 9 ) en ( 8 ), obteniendo

donde el signo indeterminado es el opuesto del de ( 9 ). Para una onda transmitida evanescente –es decir, una cuya amplitud decae a medida que $y$ aumenta– el signo indeterminado en ( 10 ) debe ser menos , por lo que el signo indeterminado en ( 9 ) debe ser más . ^{[Nota 9]}

Con el signo correcto se puede abreviar el resultado ( 10 )

dónde

y $k 0$ es el número de onda en el vacío, es decir $\,\omega /c\,.$

Por lo tanto, la onda evanescente es una onda sinusoidal plana que se propaga en la dirección $x$ , con una amplitud que decae exponencialmente en la dirección $y$ (véase la figura 9). Es evidente que la energía almacenada en esta onda también se propaga en la dirección $x$ y no cruza la interfaz. Por lo tanto, el vector de Poynting generalmente tiene un componente en la dirección $x$ , pero su componente $y tiene un valor medio de cero (aunque su componente$ $y$ instantáneo no es exactamente cero). ^[27]^[28]

La ecuación ( 11 ) indica que la amplitud de la onda evanescente disminuye en un factor $e$ a medida que la coordenada $y$ (medida desde la interfaz) aumenta en la distancia ‍ comúnmente llamada "profundidad de penetración" de la onda evanescente. ^[29] Tomando recíprocos de la primera ecuación de ( 12 ), encontramos que la profundidad de penetración es ^[28] donde λ ₀ es la longitud de onda en el vacío, es decir ^[30] Dividiendo el numerador y el denominador por $n$ $2$ se obtiene donde es la longitud de onda en el segundo medio (externo). Por lo tanto, podemos trazar $d$ en unidades de λ ₂ , como una función del ángulo de incidencia, para varios valores de (Fig. 12). A medida que θ _i disminuye hacia el ángulo crítico, el denominador se acerca a cero, de modo que $d$ aumenta sin límite, como es de esperar, porque tan pronto como θ _i es menor que el crítico, se permiten ondas planas uniformes en el medio externo. A medida que θ _i se acerca a 90° (incidencia rasante), $d$ se acerca a un mínimo. Para la incidencia del agua al aire, o del vidrio común al aire, $d$ $min$ no es muy diferente de ⁠ $d=1/\kappa \,,\,$ $d={\frac {\lambda _{0}}{2\pi \,{\sqrt {n_{1}^{2}\sin ^{2}\theta _{\text{i}}\,-\,n_{2}^{2}}}}}~,$ $\,2\pi /k_{0}\,.$ $d={\frac {\lambda _{2}}{2\pi \,{\sqrt {(n_{1}/n_{2})^{2}\sin ^{2}\theta _{\text{i}}\,-\,1}}}}~,$ $\,\lambda _{2}=\lambda _{0}/n_{2}\,$ $n_{1}/n_{2\,}$ $d_{\text{min}}={\frac {\lambda _{2}}{2\pi \,{\sqrt {(n_{1}/n_{2})^{2}-1}}}}~.$ lambda ₂/2π⁠ . Pero $d$ es mayor en ángulos de incidencia más pequeños (Fig. 12), y la amplitud puede seguir siendo significativa a distancias de varias veces $d$ ; por ejemplo, debido a que $e -4.6$ es apenas mayor que 0.01, la amplitud de onda evanescente dentro de una distancia $4.6 ‍ d$ de la interfaz es al menos el 1% de su valor en la interfaz. Por lo tanto, hablando libremente, tendemos a decir que la amplitud de onda evanescente es significativa dentro de "unas pocas longitudes de onda" de la interfaz.

Cambios de fase

Entre 1817 y 1823, Augustin-Jean Fresnel descubrió que la reflexión interna total va acompañada de un desplazamiento de fase no trivial (es decir, un desplazamiento de fase que no se limita a 0° o 180°), ya que el coeficiente de reflexión de Fresnel adquiere una parte imaginaria distinta de cero . ^[31] Ahora explicaremos este efecto para las ondas electromagnéticas en el caso de medios lineales , homogéneos , isótropos y no magnéticos. El desplazamiento de fase resulta ser un avance , que crece a medida que el ángulo de incidencia aumenta más allá del ángulo crítico, pero que depende de la polarización de la onda incidente.

En las ecuaciones ( 5 ), ( 7 ), ( 8 ), ( 10 ) y ( 11 ), adelantamos la fase por el ángulo ϕ si reemplazamos $ωt$ por $ωt+ϕ$ (es decir, si reemplazamos $-ωt$ por $-ωt-ϕ$ ), con el resultado de que el campo (complejo) se multiplica por $e -iϕ$ . Por lo tanto, un avance de fase es equivalente a la multiplicación por una constante compleja con un argumento negativo . Esto se vuelve más obvio cuando (por ejemplo) el campo ( 5 ) se factoriza como donde el último factor contiene la dependencia del tiempo. ^{[Nota 10]} $\mathbf {E_{k}} e^{i\mathbf {k\cdot r} }e^{-i\omega t},\,$

Para representar la polarización de la onda incidente, reflejada o transmitida, el campo eléctrico adyacente a una interfaz se puede descomponer en dos componentes perpendiculares, conocidos como componentes s y p , que son paralelos a la superficie y al plano de incidencia, respectivamente; en otras palabras, los componentes s y p son respectivamente cuadrados y paralelos al plano de incidencia. ^{[Nota 11]}

Para cada componente de polarización, el campo eléctrico incidente, reflejado o transmitido ( $E$ en la ecuación ( 5 ) ) tiene una dirección determinada, y puede representarse por su componente escalar (complejo) en esa dirección. El coeficiente de reflexión o transmisión puede definirse entonces como una relación de componentes complejos en el mismo punto, o en puntos infinitesimalmente separados en lados opuestos de la interfaz. Pero, para fijar los signos de los coeficientes, debemos elegir sentidos positivos para las "direcciones". Para los componentes s , la elección obvia es decir que las direcciones positivas de los campos incidente, reflejado y transmitido son todas iguales (por ejemplo, la dirección $z$ en la figura 11). Para los componentes p , este artículo adopta la convención de que las direcciones positivas de los campos incidente, reflejado y transmitido están inclinadas hacia el mismo medio (es decir, hacia el mismo lado de la interfaz, por ejemplo, como las flechas rojas en la figura 11). ^{[Nota 12]} Pero se debe advertir al lector que algunos libros utilizan una convención diferente para los componentes p , lo que provoca un signo diferente en la fórmula resultante para el coeficiente de reflexión. ^[32]

Para la polarización s , sean $r s$ y $t s$ los coeficientes de reflexión y transmisión respectivamente. Para la polarización p , sean $r p$ y $t p$ los coeficientes correspondientes . Entonces, para medios lineales , homogéneos , isótropos y no magnéticos , los coeficientes vienen dados por: ^[33]

(Para una derivación de lo anterior, véase Ecuaciones de Fresnel § Teoría ).

Ahora supongamos que la onda transmitida es evanescente. Con el signo correcto (+), sustituyendo ( 9 ) en ( 13 ) obtenemos donde es decir, $n$ es el índice del medio "interno" en relación con el "externo", o el índice del medio interno si el externo es el vacío. ^{[Nota 13]} Por lo tanto, la magnitud de $r$ $s$ es 1, y el argumento de $r$ $s$ es , lo que da un avance de fase de ‍ [^34] $r_{s}=\,{\frac {n\cos \theta _{\text{i}}-i{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}{n\cos \theta _{\text{i}}+i{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}}\,,$ $n=n_{1}/n_{2}\,;$ $-2\arctan {\frac {\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}{n\cos \theta _{\text{i}}}}\,,$

Haciendo la misma sustitución en ( 14 ), encontramos que $t s$ tiene el mismo denominador que $r s$ con un numerador real positivo (en lugar de un numerador conjugado complejo) y por lo tanto tiene la mitad del argumento de $r s ‍ ,$ ‍ de modo que el avance de fase de la onda evanescente es la mitad del de la onda reflejada .

Con la misma elección de signo, ^{[Nota 14]} sustituyendo ( 9 ) en ( 15 ) se obtiene cuya magnitud es 1, y cuyo argumento es que da un avance de fase de ‍ [^34] $r_{p}=\,{\frac {\cos \theta _{\text{i}}-in{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}{\cos \theta _{\text{i}}+in{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}}\,,$ $-2\arctan {\frac {\,n{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}{\cos \theta _{\text{i}}}}\,,$

Haciendo la misma sustitución en ( 16 ), encontramos nuevamente que el avance de fase de la onda evanescente es la mitad del de la onda reflejada.

Las ecuaciones ( 17 ) y ( 18 ) se aplican cuando $θ$ $c$ $\leq$ $θ$ $i$ $< 90°,$ donde θ _i es el ángulo de incidencia y θ _c es el ángulo crítico arcsin $(1/$ $n$ $)$ . Estas ecuaciones muestran que

cada avance de fase es cero en el ángulo crítico (para el cual el numerador es cero);
cada avance de fase se aproxima a 180° cuando $θ$ $i$ $\to 90°$ ; y
$δ p > δ s$ ‍ en valores intermedios de θ _i ( porque el factor $n$ está en el numerador de ( 18 ) y el denominador de ( 17 ) ) .^[35]

Para $θ i \leq θ c ‍ ,$ ‍ los coeficientes de reflexión están dados por las ecuaciones ( 13 ) y ( 15 ), y son reales , de modo que el desplazamiento de fase es 0° (si el coeficiente es positivo) o 180° (si el coeficiente es negativo).

En ( 13 ), si ponemos ‍ ( ley de Snell) y multiplicamos el numerador y denominador por $‍ ⁠$ $n_{2}=n_{1}\sin \theta _{\text{i}}/\sin \theta _{\text{t}}$ $1 / número 1 ⁠ sin θ t$ ‍ , obtenemos ^[36]^[37]

que es positiva para todos los ángulos de incidencia con un rayo transmitido (ya que $‍ θ$ $t$ $>$ $θ$ $i$ ), dando un desplazamiento de fase $δ$ $s$ de cero.

Si hacemos lo mismo con ( 15 ), se demuestra fácilmente que el resultado es equivalente a ^[38]^[39]

que es negativo para ángulos pequeños (es decir, incidencia cercana a la normal), pero cambia de signo en el ángulo de Brewster , donde θ _i y θ _t son complementarios. Por lo tanto, el cambio de fase $δ p$ es de 180° para θ _i pequeños, pero cambia a 0° en el ángulo de Brewster. Al combinar la complementariedad con la ley de Snell, se obtiene $‍ θ$ $i$ $= arctan (1/$ $n$ $)$ ‍ como ángulo de Brewster para incidencia de densa a rara. ^{[Nota 15]}

( Las ecuaciones ( 19 ) y ( 20 ) se conocen como ley del seno de Fresnel y ley de la tangente de Fresnel . ^[40] Ambas se reducen a 0/0 en incidencia normal, pero producen los resultados correctos en el límite cuando $‍ θ$ $i$ $\to 0.$ Que tengan signos opuestos a medida que nos acercamos a la incidencia normal es una desventaja obvia de la convención de signos utilizada en este artículo; la ventaja correspondiente es que tienen los mismos signos en incidencia rasante. )

Esto completa la información necesaria para representar gráficamente $δ s$ y $δ p$ para todos los ángulos de incidencia. Esto se hace en la Fig. 13, ^[34] con $δ p$ en rojo y $δ s$ en azul, para tres índices de refracción. En la escala de ángulo de incidencia (eje horizontal), el ángulo de Brewster es donde $δ p$ (rojo) cae de 180° a 0°, y el ángulo crítico es donde tanto $δ p$ como $δ s$ (rojo y azul) comienzan a aumentar nuevamente. A la izquierda del ángulo crítico está la región de reflexión parcial , donde ambos coeficientes de reflexión son reales (fase 0° o 180°) con magnitudes menores a 1. A la derecha del ángulo crítico está la región de reflexión total , donde ambos coeficientes de reflexión son complejos con magnitudes iguales a 1. En esa región, las curvas negras muestran el avance de fase del componente p con respecto al componente s : ^[41] Se puede observar que un índice de refracción de 1,45 no es suficiente para dar una diferencia de fase de 45°, mientras que un índice de refracción de 1,5 es suficiente (por un margen estrecho) para dar una diferencia de fase de 45° en dos ángulos de incidencia: aproximadamente 50,2° y 53,3°. $\delta =\delta _{p\!}-\delta _{s}\,.$

Este desplazamiento relativo de 45° se emplea en la invención de Fresnel, ahora conocida como el rombo de Fresnel, en el que los ángulos de incidencia se eligen de modo que las dos reflexiones internas provoquen un desplazamiento de fase relativo total de 90° entre las dos polarizaciones de una onda incidente. Este dispositivo realiza la misma función que una placa de cuarto de onda birrefringente , pero es más acromático (es decir, el desplazamiento de fase del rombo es menos sensible a la longitud de onda ). Cualquiera de los dos dispositivos puede utilizarse, por ejemplo, para transformar la polarización lineal en polarización circular (que Fresnel también descubrió) y viceversa.

En la figura 13, $δ$ se calcula mediante una resta final; pero hay otras formas de expresarlo. El propio Fresnel, en 1823, ^[42] dio una fórmula para $cos δ$ . Born y Wolf (1970, p. 50) derivan una expresión para ‍ tan $(δ /2),$ y encuentran su máximo analíticamente.

Para la TIR de un haz con ancho finito, la variación en el desplazamiento de fase con el ángulo de incidencia da lugar al efecto Goos–Hänchen , que es un desplazamiento lateral del haz reflejado dentro del plano de incidencia. ^[28]^[43] Este efecto se aplica a la polarización lineal en la dirección s o p . El efecto Imbert–Fedorov es un efecto análogo para la polarización circular o elíptica , y produce un desplazamiento perpendicular al plano de incidencia. ^[44]

Aplicaciones

Las fibras ópticas aprovechan la reflexión interna total para transportar señales a largas distancias con poca atenuación.^[45] Se utilizan en cables de telecomunicaciones y en fibroscopios formadores de imágenes, como los colonoscopios .^[46]

En la lente catadióptrica de Fresnel , inventada por Augustin-Jean Fresnel para su uso en faros , los prismas exteriores utilizan TIR para desviar la luz de la lámpara a través de un ángulo mayor del que sería posible con prismas puramente refractivos, pero con menor absorción de luz (y menos riesgo de empañamiento) que con espejos convencionales. ^[47]

Otros prismas reflectores que utilizan TIR incluyen los siguientes (con cierta superposición entre las categorías): ^[48]

Los prismas de formación de imágenes para binoculares y telescopios terrestres incluyen prismas Porro emparejados de 45°-90°-45°(Fig. 14), el prisma Porro-Abbe , los prismas en línea Koenig^[49] y Abbe-Koenig , y el prisma compacto en línea Schmidt-Pechan . (El último consta de dos componentes, de los cuales uno es un tipo de prisma Bauernfeind , que requiere un revestimiento reflectante en una de sus dos caras reflectantes, debido a un ángulo de incidencia subcrítico). Estos prismas tienen la función adicional de plegar la trayectoria óptica desde la lente del objetivo hasta el foco principal , reduciendo la longitud total para una distancia focal primaria dada.
Una diagonal estelar prismática para un telescopio astronómico puede consistir en un solo prisma Porro (configurado para una única reflexión, dando una imagen invertida en espejo) o un prisma de techo Amici (que da una imagen no invertida).
Los prismas de techo utilizan TIR en dos caras que se encuentran en un ángulo agudo de 90°. Esta categoría incluye los tipos Koenig, Abbe–Koenig, Schmidt–Pechan y Amici (ya mencionados), y el pentaprisma de techo utilizado en las cámaras SLR ; este último requiere un revestimiento reflectante en una cara que no es TIR .
Un reflector de esquina prismático utiliza tres reflexiones internas totales para invertir la dirección de la luz entrante.
El prisma Dove proporciona una visión en línea con inversión del espejo.

Prismas polarizadores : Aunque el rombo de Fresnel, que convierte entre polarización lineal y elíptica, no es birrefringente (doblemente refractivo), existen otros tipos de prismas que combinan la birrefringencia con la TIR de tal manera que la luz de una polarización particular se refleja totalmente mientras que la luz de la polarización ortogonal se transmite al menos parcialmente. Algunos ejemplos incluyen el prisma de Nicol , ^[50] el prisma de Glan–Thompson , el prisma de Glan–Foucault (o "prisma de Foucault"), ^[51]^[52] y el prisma de Glan–Taylor . ^[53]

Los refractómetros , que miden los índices de refracción, a menudo utilizan el ángulo crítico.^[54]^[55]

Se han implementado sensores de lluvia para limpiaparabrisas automáticos utilizando el principio de que la reflexión interna total guiará un haz infrarrojo desde una fuente a un detector si la superficie exterior del parabrisas está seca, pero cualquier gota de agua en la superficie desviará parte de la luz.^[56]

Los paneles LED con iluminación de borde , utilizados (por ejemplo) para la retroiluminación de monitores de computadora LCD , aprovechan la TIR para confinar la luz LED al panel de vidrio acrílico, excepto que parte de la luz se dispersa mediante grabados en un lado del panel, lo que da una emisión luminosa aproximadamente uniforme . ^[57]

La microscopía de reflexión interna total (TIRM) utiliza la onda evanescente para iluminar objetos pequeños cercanos a la interfaz reflectante. La dispersión consecuente de la onda evanescente (una forma de TIR frustrada) hace que los objetos parezcan brillantes cuando se los observa desde el lado "externo". ^[21] En el microscopio de fluorescencia de reflexión interna total (TIRFM), en lugar de confiar en la dispersión simple, elegimos una longitud de onda evanescente lo suficientemente corta como para causar fluorescencia (Fig. 15). ^[58] La alta sensibilidad de la iluminación a la distancia desde la interfaz permite la medición de desplazamientos y fuerzas extremadamente pequeños. ^[59]

Un cubo divisor de haz utiliza TIR frustrado para dividir la potencia del haz entrante entre los haces transmitidos y reflejados. ^[18] El ancho del espacio de aire (o espacio de bajo índice de refracción) entre los dos prismas se puede ajustar, lo que da una mayor transmisión y una menor reflexión para un espacio más estrecho, o una mayor reflexión y una menor transmisión para un espacio más amplio. ^[60]

La modulación óptica se puede lograr por medio de TIR frustrado con un espacio rápidamente variable.^[61] Como el coeficiente de transmisión es altamente sensible al ancho del espacio (la función es aproximadamente exponencial hasta que el espacio está casi cerrado), esta técnica puede lograr un amplio rango dinámico .

Los dispositivos de toma de huellas dactilares ópticas han utilizado TIR frustrado para registrar imágenes de huellas dactilares de personas sin el uso de tinta (cf. Fig. 11). ^[62]

El análisis de la marcha se puede realizar utilizando TIR frustrado con una cámara de alta velocidad, para capturar y analizar huellas.^[63]

Un gonioscopio , utilizado en optometría y oftalmología para el diagnóstico del glaucoma , suprime la TIR para poder observar el ángulo entre el iris y la córnea . Esta visión suele estar bloqueada por la TIR en la interfaz córnea-aire. El gonioscopio reemplaza el aire con un medio de índice más alto, lo que permite la transmisión en incidencia oblicua, generalmente seguida de reflexión en un "espejo", que a su vez puede implementarse utilizando la TIR. ^[64]^[65]

Algunas mesas interactivas y pizarras multitáctiles utilizan FTIR para detectar los dedos que tocan la pantalla. Se coloca una cámara infrarroja detrás de la superficie de la pantalla, que está iluminada por los bordes con LED infrarrojos; cuando se toca la superficie, FTIR hace que parte de la luz infrarroja escape del plano de la pantalla y la cámara la ve como áreas brillantes. Luego se utiliza un software de visión artificial para traducir esto en una serie de coordenadas y gestos.

Historia

Descubrimiento

Las explicaciones sorprendentemente completas y en gran parte correctas del arco iris por Teodorico de Friburgo (escritas entre 1304 y 1310) ^[66] y Kamāl al-Dīn al-Fārisī (completada en 1309), ^[67] aunque a veces se mencionan en relación con la reflexión interna total (TIR), son de dudosa relevancia porque la reflexión interna de la luz solar en una gota de lluvia esférica no es total. ^{[Nota 16]} Pero, según Carl Benjamin Boyer , el tratado de Teodorico sobre el arco iris también clasificó los fenómenos ópticos bajo cinco causas, la última de las cuales era "una reflexión total en el límite de dos medios transparentes". ^[68] El trabajo de Teodorico fue olvidado hasta que fue redescubierto por Giovanni Battista Venturi en 1814. ^[69]

Como Teodorico había caído en el olvido, el descubrimiento de la TIR se atribuyó generalmente a Johannes Kepler , que publicó sus hallazgos en su Dióptrica en 1611. Aunque Kepler no logró encontrar la verdadera ley de refracción, demostró mediante experimentos que, en el caso de la incidencia del aire sobre el vidrio, los rayos incidente y refractado rotaban en el mismo sentido alrededor del punto de incidencia, y que, como el ángulo de incidencia variaba en ±90°, el ángulo de refracción (como lo llamamos ahora) variaba en ±42°. También era consciente de que los rayos incidente y refractado eran intercambiables. Pero estas observaciones no cubrían el caso de un rayo incidente del vidrio al aire en un ángulo superior a 42°, y Kepler concluyó rápidamente que un rayo de este tipo solo podía reflejarse . ^[70]

René Descartes redescubrió la ley de refracción y la publicó en su Dioptrique de 1637. En la misma obra mencionó los sentidos de rotación de los rayos incidente y refractado y la condición de TIR. Pero olvidó analizar el caso límite y, en consecuencia, no dio una expresión para el ángulo crítico, aunque podría haberlo hecho fácilmente. ^[71]

Huygens y Newton: explicaciones rivales

Christiaan Huygens , en su Tratado sobre la luz (1690), prestó mucha atención al umbral en el que el rayo incidente es "incapaz de penetrar en la otra sustancia transparente". ^[72] Aunque no dio un nombre ni una expresión algebraica para el ángulo crítico, dio ejemplos numéricos para la incidencia vidrio-aire y agua-aire, notó el gran cambio en el ángulo de refracción para un pequeño cambio en el ángulo de incidencia cerca del ángulo crítico, y citó esto como la causa del rápido aumento en el brillo del rayo reflejado a medida que el rayo refractado se acerca a la tangente a la interfaz. ^[73] La idea de Huygens es confirmada por la teoría moderna: en las ecuaciones ( 13 ) y ( 15 ) anteriores, no hay nada que diga que los coeficientes de reflexión aumentan excepcionalmente abruptamente a medida que θ _t se acerca a 90°, excepto que, según la ley de Snell, θ _t en sí mismo es una función cada vez más pronunciada de θ _i .

Huygens ofreció una explicación de la TIR dentro del mismo marco que sus explicaciones de las leyes de propagación rectilínea, reflexión, refracción ordinaria e incluso la refracción extraordinaria del " cristal de Islandia " (calcita). Ese marco se basaba en dos premisas: primero, cada punto atravesado por un frente de onda en propagación se convierte en una fuente de frentes de onda secundarios ("principio de Huygens"); y segundo, dado un frente de onda inicial, cualquier posición posterior del frente de onda es la envolvente (superficie tangente común) de todos los frentes de onda secundarios emitidos desde la posición inicial. Todos los casos de reflexión o refracción por una superficie se explican entonces simplemente considerando las ondas secundarias emitidas desde esa superficie. En el caso de la refracción desde un medio de propagación más lenta a un medio de propagación más rápida, existe una cierta oblicuidad de incidencia más allá de la cual es imposible que los frentes de onda secundarios formen una tangente común en el segundo medio; ^[74] esto es lo que ahora llamamos el ángulo crítico. A medida que el frente de onda incidente se acerca a esta oblicuidad crítica, el frente de onda refractado se concentra contra la superficie refractante, aumentando las ondas secundarias que producen la reflexión en el primer medio. ^[75]

El sistema de Huygens incluso acomodó la reflexión parcial en la interfaz entre diferentes medios, aunque vagamente, por analogía con las leyes de colisiones entre partículas de diferentes tamaños. ^[76] Sin embargo, mientras la teoría ondulatoria continuó asumiendo ondas longitudinales , no tuvo posibilidad de acomodar la polarización, por lo tanto, no tuvo posibilidad de explicar la dependencia de la polarización de la refracción extraordinaria, ^[77] o del coeficiente de reflexión parcial, o del cambio de fase en TIR.

Isaac Newton rechazó la explicación ondulatoria de la propagación rectilínea, creyendo que si la luz consistiera en ondas, se "doblaría y se extendería en todas direcciones" hacia las sombras. ^[78] Su teoría corpuscular de la luz explicaba la propagación rectilínea de forma más sencilla, y daba cuenta de las leyes ordinarias de refracción y reflexión, incluida la TIR, sobre la hipótesis de que los corpúsculos de luz estaban sujetos a una fuerza que actuaba perpendicularmente a la interfaz. ^[79] En este modelo, para la incidencia de densa a rara, la fuerza era una atracción hacia el medio más denso, y el ángulo crítico era el ángulo de incidencia en el que la velocidad normal del corpúsculo que se aproximaba era suficiente para alcanzar el lado más alejado del campo de fuerza; en una incidencia más oblicua, el corpúsculo se volvería hacia atrás. ^[80] Newton dio lo que equivale a una fórmula para el ángulo crítico, aunque en palabras: "como los senos miden la refracción, así es el seno de incidencia en el que comienza la reflexión total, con respecto al radio del círculo". ^[81]

Newton fue más allá de Huygens en dos aspectos. En primer lugar, y como era de esperar, Newton señaló la relación entre la TIR y la dispersión : cuando un haz de luz blanca se acerca a una interfaz vidrio-aire con una oblicuidad creciente, los rayos más fuertemente refractados (violetas) son los primeros en ser "eliminados" por la "reflexión total", seguidos por los rayos menos refractados. ^[82] En segundo lugar, observó que la reflexión total podía verse frustrada (como decimos ahora) colocando juntos dos prismas, uno plano y el otro ligeramente convexo; y lo explicó simplemente señalando que los corpúsculos serían atraídos no sólo por el primer prisma, sino también por el segundo. ^[83]

Sin embargo, en otros dos aspectos el sistema de Newton era menos coherente. En primer lugar, su explicación de la reflexión parcial dependía no sólo de las supuestas fuerzas de atracción entre corpúsculos y medios, sino también de la hipótesis más nebulosa de los “Accidentes de fácil reflexión” y los “Accidentes de fácil transmisión”. ^[84] En segundo lugar, aunque sus corpúsculos podrían tener “lados” o “polos”, cuyas orientaciones podrían determinar si los corpúsculos sufrían una refracción ordinaria o extraordinaria en la “Isla-Cristal”, ^[85] su descripción geométrica de la refracción extraordinaria ^[86] no tenía respaldo teórico ^[87] y era empíricamente inexacta. ^[88]

Reflectancia total atenuada (ATR), Laplace y Malus

William Hyde Wollaston , en el primero de un par de artículos presentados en la Royal Society de Londres en 1802, ^[55] informó de su invención de un refractómetro basado en el ángulo crítico de incidencia de un medio interno de "poder refractivo" conocido (índice de refracción) a un medio externo cuyo índice se iba a medir. ^[89] Con este dispositivo, Wollaston midió los "poderes refractivos" de numerosos materiales, algunos de los cuales eran demasiado opacos para permitir la medición directa de un ángulo de refracción. Las traducciones de sus artículos se publicaron en Francia en 1803 y, aparentemente, llegaron a la atención de Pierre-Simon Laplace . ^[90]

Según la elaboración que hizo Laplace de la teoría de la refracción de Newton, un corpúsculo incidente en una interfaz plana entre dos medios isótropos homogéneos estaba sujeto a un campo de fuerza que era simétrico con respecto a la interfaz. Si ambos medios fueran transparentes, se produciría una reflexión total si el corpúsculo se girara hacia atrás antes de que saliera del campo en el segundo medio. Pero si el segundo medio fuera opaco, la reflexión no sería total a menos que el corpúsculo se girara hacia atrás antes de que abandonara el primer medio; esto requería un ángulo crítico mayor que el dado por la ley de Snell y, en consecuencia, cuestionaba la validez del método de Wollaston para medios opacos. ^[91] Laplace combinó los dos casos en una única fórmula para el índice de refracción relativo en términos del ángulo crítico (ángulo mínimo de incidencia para TIR). La fórmula contenía un parámetro que tomaba un valor para un medio externo transparente y otro valor para un medio externo opaco. La teoría de Laplace predijo además una relación entre el índice de refracción y la densidad para una sustancia dada. ^[92]

En 1807, la teoría de Laplace fue puesta a prueba experimentalmente por su protegido, Étienne-Louis Malus . Tomando la fórmula de Laplace para el índice de refracción como dada y utilizándola para medir el índice de refracción de la cera de abejas en estado líquido (transparente) y en estado sólido (opaco) a varias temperaturas (y, por lo tanto, a varias densidades), Malus verificó la relación de Laplace entre el índice de refracción y la densidad. ^[93]^[94]

Pero la teoría de Laplace implicaba que si el ángulo de incidencia excedía su ángulo crítico modificado, la reflexión sería total incluso si el medio externo era absorbente. Claramente esto era erróneo: en las ecuaciones ( 12 ) anteriores, no hay un valor umbral del ángulo θ _i más allá del cual κ se vuelve infinito; por lo tanto, la profundidad de penetración de la onda evanescente (1/ κ ) siempre es distinta de cero, y el medio externo, si tiene alguna pérdida, atenuará la reflexión. En cuanto a por qué Malus aparentemente observó tal ángulo para la cera opaca, debemos inferir que había un cierto ángulo más allá del cual la atenuación de la reflexión era tan pequeña que la ATR era visualmente indistinguible de la TIR. ^[95]

Fresnel y el cambio de fase

Fresnel llegó al estudio de la reflexión interna total a través de su investigación sobre la polarización. En 1811, François Arago descubrió que la luz polarizada aparentemente se "despolarizaba" de una manera dependiente de la orientación y del color cuando pasaba a través de una rebanada de cristal doblemente refractivo: la luz emergente mostraba colores cuando se veía a través de un analizador (segundo polarizador). La polarización cromática , como se llegó a llamar a este fenómeno, fue investigada más a fondo en 1812 por Jean-Baptiste Biot . En 1813, Biot estableció que un caso estudiado por Arago, concretamente el cuarzo cortado perpendicularmente a su eje óptico , era en realidad una rotación gradual del plano de polarización con la distancia. ^[96]

En 1816, Fresnel ofreció su primer intento de una teoría de polarización cromática basada en ondas . Sin invocar (todavía) explícitamente ondas transversales , su teoría trataba la luz como si estuviera formada por dos componentes polarizados perpendicularmente. ^[97] En 1817 se dio cuenta de que la luz polarizada en un plano parecía estar parcialmente despolarizada por la reflexión interna total, si inicialmente se polarizaba en un ángulo agudo con respecto al plano de incidencia. ^[98] Al incluir la reflexión interna total en un experimento de polarización cromática, descubrió que la luz aparentemente despolarizada era una mezcla de componentes polarizados en paralelo y en perpendicular al plano de incidencia, y que la reflexión total introducía una diferencia de fase entre ellos. ^[99] La elección de un ángulo de incidencia apropiado (aún no especificado con exactitud) dio una diferencia de fase de 1/8 de ciclo. Dos de esas reflexiones de las "caras paralelas" de "dos prismas acoplados" dieron una diferencia de fase de 1/4 de ciclo. En ese caso, si la luz estaba inicialmente polarizada a 45° respecto del plano de incidencia y reflexión, parecía estar completamente despolarizada después de las dos reflexiones. Estos hallazgos se informaron en una memoria presentada y leída en la Academia Francesa de Ciencias en noviembre de 1817. ^[100]

En 1821, Fresnel derivó fórmulas equivalentes a sus leyes del seno y la tangente ( Ecs. ( 19 ) y ( 20 ), arriba ) al modelar las ondas de luz como ondas elásticas transversales con vibraciones perpendiculares a lo que previamente se había llamado el plano de polarización . ^[101]^{[Nota 17]} Utilizando viejos datos experimentales, rápidamente confirmó que las ecuaciones predecían correctamente la dirección de polarización del haz reflejado cuando el haz incidente estaba polarizado a 45° respecto del plano de incidencia, para la luz incidente desde el aire sobre vidrio o agua. ^[102] La confirmación experimental fue reportada en una "posdata" al trabajo en el que Fresnel expuso su teoría madura de la polarización cromática, introduciendo ondas transversales. ^[103] Los detalles de la derivación se dieron más tarde, en una memoria leída en la academia en enero de 1823. ^[104] La derivación combinó la conservación de la energía con la continuidad de la vibración tangencial en la interfaz, pero no tuvo en cuenta ninguna condición en el componente normal de la vibración. ^[105]

Mientras tanto, en una memoria presentada en diciembre de 1822, ^[106] Fresnel acuñó los términos polarización lineal , polarización circular y polarización elíptica . ^[107] Para la polarización circular , los dos componentes perpendiculares estaban desfasados un cuarto de ciclo (±90°).

La nueva terminología fue útil en las memorias de enero de 1823, ^[104] que contenían las derivaciones detalladas de las leyes del seno y la tangente: en esas mismas memorias, Fresnel descubrió que para ángulos de incidencia mayores que el ángulo crítico, los coeficientes de reflexión resultantes eran complejos con magnitud unitaria. Al notar que la magnitud representaba la relación de amplitud como de costumbre, supuso que el argumento representaba el cambio de fase y verificó la hipótesis mediante un experimento. ^[108] La verificación implicó

calcular el ángulo de incidencia que introduciría una diferencia de fase total de 90° entre los componentes s y p , para varios números de reflexiones internas totales en ese ángulo (generalmente había dos soluciones),
sometiendo la luz a ese número de reflexiones internas totales en ese ángulo de incidencia, con una polarización lineal inicial a 45° respecto del plano de incidencia, y
comprobando que la polarización final era circular. ^[109]

Este procedimiento era necesario porque, con la tecnología de la época, no se podían medir directamente los desfases s y p , ni tampoco se podía medir un grado arbitrario de elipticidad de la polarización, como podría ser causado por la diferencia entre los desfases. Pero se podía verificar que la polarización era circular , porque el brillo de la luz era entonces insensible a la orientación del analizador.

Para un vidrio con un índice de refracción de 1,51, Fresnel calculó que una diferencia de fase de 45° entre los dos coeficientes de reflexión (por lo tanto, una diferencia de 90° después de dos reflexiones) requería un ángulo de incidencia de 48°37' o 54°37'. Cortó un rombo con este último ángulo y descubrió que funcionaba como se esperaba. ^[110] De esta manera, se completó la especificación del rombo de Fresnel. De manera similar, Fresnel calculó y verificó el ángulo de incidencia que daría una diferencia de fase de 90° después de tres reflexiones en el mismo ángulo y cuatro reflexiones en el mismo ángulo. En cada caso hubo dos soluciones y en cada caso informó que el ángulo de incidencia más grande daba una polarización circular precisa (para una polarización lineal inicial a 45° con respecto al plano de reflexión). Para el caso de tres reflexiones, también probó el ángulo más pequeño, pero descubrió que daba cierta coloración debido a la proximidad del ángulo crítico y su ligera dependencia de la longitud de onda. (Compare la Figura 13 anterior, que muestra que la diferencia de fase $δ$ es más sensible al índice de refracción para ángulos de incidencia más pequeños).

Para mayor confianza, Fresnel predijo y verificó que cuatro reflexiones internas totales a 68°27' darían una polarización circular precisa si dos de las reflexiones tuvieran agua como medio externo mientras que las otras dos tuvieran aire, pero no si las superficies reflectantes estuvieran todas húmedas o todas secas. ^[111]

Se cree que la deducción de Fresnel del cambio de fase en TIR fue la primera ocasión en la que se le dio un significado físico al argumento de un número complejo. Aunque este razonamiento se aplicó sin el beneficio de saber que las ondas de luz eran electromagnéticas, pasó la prueba del experimento y sobrevivió notablemente intacto después de que James Clerk Maxwell cambiara la naturaleza presunta de las ondas. ^[112] Mientras tanto, el éxito de Fresnel inspiró a James MacCullagh y Augustin-Louis Cauchy , a partir de 1836, a analizar la reflexión de los metales utilizando las ecuaciones de Fresnel con un índice de refracción complejo . ^[113] La parte imaginaria del índice complejo representa la absorción. ^[114]

El término ángulo crítico , utilizado por conveniencia en la narración anterior, es anacrónico: aparentemente data de 1873. ^[115]

En el siglo XX, la electrodinámica cuántica reinterpretó la amplitud de una onda electromagnética en términos de la probabilidad de encontrar un fotón. ^[116] En este marco, la transmisión parcial y la TIR frustrada se refieren a la probabilidad de que un fotón cruce un límite, y la reflectancia total atenuada se refiere a la probabilidad de que un fotón sea absorbido en el otro lado.

La investigación sobre los aspectos más sutiles del cambio de fase en TIR, incluidos los efectos Goos-Hänchen e Imbert-Fedorov y sus interpretaciones cuánticas, ha continuado hasta el siglo XXI. ^[44]

Galería

Un pez ballesta indio y su reflejo total en la superficie del agua.
Reflexión total de un pincel sobre la superficie agua-aire en un vaso
Reflexión interna total de un láser verde en el tallo de una copa de vino

Véase también

Notas

^ Los medios birrefringentes , como la calcita , no son isotrópicos (son anisotrópicos). Cuando decimos que la refracción extraordinaria de un cristal de calcita "viola la ley de Snell", queremos decir que la ley de Snell no se aplica al rayo extraordinario , porque la dirección de este rayo dentro del cristal generalmente difiere de la de la onda normal asociada (Huygens, 1690, tr. Thompson, p. 65, Art. 24), y porque la velocidad de la onda normal depende de la dirección. (Obsérvese que el pasaje citado contiene un error de traducción: en la frase "conjugado con respecto a diámetros que no están en la línea recta AB", la palabra "no" no está respaldada por el francés original de Huygens y es geométricamente incorrecta).
^ Según las ecuaciones ( 13 ) y ( 15 ), la reflexión es total para la incidencia en el ángulo crítico. Sobre esa base, la figura 5 debería mostrar un rayo totalmente reflejado, y ningún rayo tangencial, para la incidencia en θ _c . Pero, debido a la difracción , un rayo incidente de ancho finito no puede tener un solo ángulo de incidencia; debe haber alguna divergencia del rayo. Además, el gráfico del coeficiente de reflexión frente al ángulo de incidencia se vuelve vertical en θ _c (Jenkins y White, 1976, pág. 527), de modo que una pequeña divergencia del rayo causa una gran pérdida de reflexión. De manera similar, cerca del ángulo crítico, una pequeña divergencia en el ángulo de incidencia causa una gran divergencia en el ángulo de refracción (cf. Huygens, 1690, tr. Thompson, pág. 41); por lo tanto, el rayo refractado tangencial debería tomarse solo como un caso límite.
^ Para medios no isotrópicos, la ecuación ( 1 ) todavía describe la ley de refracción en términos de direcciones y velocidades normales de onda , pero el rango de aplicabilidad de esa ley está determinado por las restricciones en las direcciones de los rayos (cf. Buchwald, 1989, pág. 29).
^ El rango citado varía debido a los diferentes politipos de cristal .
^ La potencia "por unidad de área" es apropiada para campos en tres dimensiones. En dos dimensiones, podríamos querer que el producto del esfuerzo y el flujo sea potencia por unidad de longitud . En una dimensión, o en un modelo de elementos concentrados , podríamos querer que sea simplemente potencia.
^ Suponemos que las ecuaciones que describen los campos son lineales .
^ La forma anterior ( 5 ) es la que suelen utilizar los físicos. Los ingenieros eléctricos suelen preferir la forma en la que no sólo utilizan $j$ en lugar de $i$ para la unidad imaginaria, sino que también cambian el signo del exponente, con el resultado de que toda la expresión se sustituye por su conjugado complejo , dejando la parte real sin cambios. La forma de los ingenieros eléctricos y las fórmulas derivadas de ella se pueden convertir a la convención de los físicos sustituyendo $-i$ por $j$ (Stratton, 1941, pp. vii–viii). $\mathbf {E_{k}} e^{j(\omega t-\mathbf {k\cdot r} )};$
^ Suponemos que no hay desplazamientos Doppler , por lo que ω no cambia en las interfaces entre los medios.
^ Si convertimos esto correctamente a la convención de ingeniería eléctrica, obtenemos $-j ‍ \sqrt \dots$ en el lado derecho de ( 9 ), que no es la raíz cuadrada principal. Por lo tanto, no es válido suponer, a priori , que lo que los matemáticos llaman la " raíz cuadrada principal " es la físicamente aplicable.
^ En la convención de ingeniería eléctrica, el factor dependiente del tiempo es $e ‍ jωt,$ de modo que un avance de fase corresponde a la multiplicación por una constante compleja con un argumento positivo . Este artículo, sin embargo, utiliza la convención de física, con el factor dependiente del tiempo $e -iωt$ .
^ La s proviene originalmente del alemán senkrecht , que significa "perpendicular" (al plano de incidencia). Las mnemotecnias alternativas del texto son quizás más adecuadas para los angloparlantes.
^ En otras palabras, para ambas polarizaciones, este artículo utiliza la convención de que las direcciones positivas de los campos incidente, reflejado y transmitido son todas las mismas para cualquier campo que sea normal al plano de incidencia; este es el campo $E$ para la polarización s y el campo $H$ para la polarización p .
^ Esta nomenclatura sigue a Jenkins & White, 1976, pp. 526–9. Sin embargo, algunos autores utilizan el índice de refracción recíproco y, por lo tanto, obtienen formas diferentes para nuestras ecuaciones ( 17 ) y ( 18 ). Los ejemplos incluyen Born & Wolf [1970, p. 49, ecuaciones (60)] ‍ y Stratton [1941, p. 499, ecuaciones (43)]. Además, Born & Wolf definen $δ ⊥$ y $δ ∥$ como argumentos en lugar de cambios de fase, lo que provoca un cambio de signo.
^ Es meramente fortuito que la raíz cuadrada principal resulte ser la correcta en la situación actual, y solo porque usamos el factor dependiente del tiempo $e -iωt$ . Si en cambio usáramos el factor dependiente del tiempo de los ingenieros eléctricos $e ‍ jωt$ , elegir la raíz cuadrada principal produciría el mismo argumento para el coeficiente de reflexión, pero esto se interpretaría como el cambio de fase opuesto , lo cual sería incorrecto. Pero si elegimos la raíz cuadrada de modo que el campo transmitido sea evanescente, obtenemos el cambio de fase correcto con cualquiera de los dos factores dependientes del tiempo.
^ La fórmula más conocida $arctan n$ ‍ es para la incidencia de rara a densa. En ambos casos, $n$ es el índice de refracción del medio más denso en relación con el medio más raro.
^ Para un rayo externo incidente sobre una gota de lluvia esférica, el rayo refractado está en el plano del rayo incidente y el centro de la gota, y el ángulo de refracción es menor que el ángulo crítico para la incidencia agua-aire; pero este ángulo de refracción, por la simetría esférica, es también el ángulo de incidencia para la reflexión interna, que es por lo tanto menor que la total. Además, si esa reflexión fuera total, todas las reflexiones internas posteriores tendrían el mismo ángulo de incidencia (debido a la simetría) y también serían totales, de modo que la luz nunca escaparía para producir un arco visible.
^ Por lo tanto, cuando Fresnel dice que después de la reflexión interna total en la incidencia apropiada, la onda polarizada paralela al plano de incidencia está "atrasada" en 1/8 de un ciclo (citado por Buchwald, 1989, p. 381), se refiere a la onda cuyo plano de polarización es paralelo al plano de incidencia, es decir, la onda cuya vibración es perpendicular a ese plano, es decir, lo que ahora llamamos el componente s .

Referencias

^ ab RP Feynman, RB Leighton y M. Sands, 1963–2013, The Feynman Lectures on Physics , Instituto Tecnológico de California, Volumen II , § 33-6.
^ Antich, Peter P.; Anderson, Jon A.; Ashman, Richard B.; Dowdey, James E.; Gonzales, Jerome; Murry, Robert C.; Zerwekh, Joseph E.; Pak, Charles YC (2009). "Medición de propiedades mecánicas de material óseo in vitro por reflexión ultrasónica: metodología y comparación con transmisión ultrasónica". Revista de investigación ósea y mineral . 6 (4): 417–426. doi :10.1002/jbmr.5650060414. PMID 1858525. S2CID 6914223..
^ Jenkins y White, 1976, pág. 11.
^ Jenkins y White, 1976, pág. 527. (El haz refractado se vuelve más débil en términos de potencia total, pero no necesariamente en términos de visibilidad, porque el haz también se vuelve más estrecho a medida que se vuelve más cercano a la tangencial).
^ Jenkins y White, 1976, pág. 26.
^ Cf. Thomas Young en Quarterly Review , abril de 1814, reimpreso en T. Young (ed. G. Peacock), Miscellaneous Works of the late Thomas Young , Londres: J. Murray, 1855, vol. 1, pág. 263.
^ Cf. Born & Wolf, 1970, págs. 12-13.
^ Cf. Huygens, 1690, trad. Thompson, pág. 38.
^ Born & Wolf, 1970, p. 13; Jenkins & White, 1976, pp. 9-10. Esta definición utiliza el vacío como "medio de referencia". En principio, se puede elegir como referencia cualquier medio isótropo. Para algunos propósitos es conveniente elegir el aire, en el que la velocidad de la luz es aproximadamente un 0,03% menor que en el vacío (cf. Rutten y van Venrooij, 2002, pp. 10, 352). Sin embargo, en el presente artículo se elige el vacío.
^ Cf. Jenkins y White, 1976, pág. 25.
^ Jenkins y White, 1976, págs. 10, 25.
^ Cf. DK Lynch (1 de febrero de 2015), "La ventana de Snell en agua ondulada", Applied Optics , 54 (4): B8–B11, doi :10.1364/AO.54.0000B8.
^ Huygens (1690, tr. Thompson, p. 41), en relación con la incidencia vidrio-aire, observó que si la oblicuidad del rayo incidente es sólo 1° menor que la crítica, el rayo refractado se encuentra a más de 11° de la tangente. NB: La definición de Huygens del "ángulo de incidencia" es el complemento de la definición moderna.
^ JR Graham, "¿Se puede cortar un diseño de gema para lograr un brillo inclinado?", International Gem Society, consultado el 21 de marzo de 2019; archivado el 14 de diciembre de 2018.
^ 'PJS' (autor), "Presión sonora, potencia sonora e intensidad sonora: ¿cuál es la diferencia?" Siemens PLM Community , consultado el 10 de abril de 2019; archivado el 10 de abril de 2019.
^ Stratton, 1941, págs. 131–7.
^ Stratton, 1941, pág. 37.
^ abc Cf. Harvard Natural Sciences Lecture Demonstrations, "Frustrated Total Internal Reflection", consultado el 9 de abril de 2019; archivado el 2 de agosto de 2018.
^ ab R. Ehrlich, 1997, Por qué las tostadas caen con el lado gelatinoso hacia abajo: el zen y el arte de las demostraciones de física , Princeton University Press, ISBN 978-0-691-02891-0 , pág. 182, consultado el 26 de marzo de 2019.
^ R. Bowley, 2009, "Total Internal Reflection" (video de 4 minutos), Sixty Symbols , Brady Haran para la Universidad de Nottingham , desde 1:25.
^ ab EJ Ambrose (24 de noviembre de 1956), "Un microscopio de contacto de superficie para el estudio de los movimientos celulares", Nature , 178 (4543): 1194, Bibcode :1956Natur.178.1194A, doi : 10.1038/1781194a0 , PMID 13387666, S2CID 4290898.
^ Van Rosum, Aernout; Van Den Berg, Ed (mayo de 2021). "Uso de la reflexión interna frustrada como análogo al efecto túnel cuántico". Journal of Physics: Conference Series . 1929 (1): 012050. Bibcode :2021JPhCS1929a2050V. doi : 10.1088/1742-6596/1929/1/012050 . S2CID 235591328.
^ Thermo Fisher Scientific, "Técnicas de muestreo FTIR: reflexión total atenuada (ATR)", consultado el 9 de abril de 2019.
^ Jenkins y White, 1976, pág. 228.
^ Born & Wolf, 1970, págs. 16-17, ecs. (20), (21).
^ Born & Wolf, 1970, p. 47, ecuación (54), donde su $n$ es nuestro ( no nuestro ). $n_{2}/n_{1}$ $n_{1}/n_{2}$
^ Stratton, 1941, pág. 499; Born & Wolf, 1970, pág. 48.
^ abc Laboratory of Cold Atoms Near Surfaces (Jagiellonian University), "Evanescent wave properties", consultado el 11 de abril de 2019; archivado el 28 de abril de 2018. ( NB: Esta página utiliza $z$ para la coordenada normal a la interfaz y los superíndices ⊥ y ∥ para las polarizaciones s ("TE") y p , respectivamente. Las páginas de este sitio utilizan el factor dependiente del tiempo $e + iωt$ , es decir, el factor dependiente del tiempo de los ingenieros eléctricos con el símbolo de los físicos para la unidad imaginaria).
^ Hecht, 2017, pág. 136.
^ Born & Wolf, 1970, pág. 16.
^ Whittaker, 1910, págs. 132, 135–6.
^ Una autoridad notable que utiliza la convención "diferente" (pero sin llevarla muy lejos) es The Feynman Lectures on Physics , en el Volumen I , ecuación (33.8) (para $B$ ), y el Volumen II , figuras 33-6 y 33-7.
^ Born & Wolf, 1970, p. 40, ecuaciones (20), (21), donde el subíndice ⊥ corresponde a s , y ∥ a p .
^ abc Cf. Jenkins y White, 1976, pág. 529.
^ "La fase de la polarización en la que el campo magnético es paralelo a la interfaz está adelantada con respecto a la de la otra polarización". — Fitzpatrick, 2013, pág. 140; Fitzpatrick, 2013a; énfasis añadido.
^ Fresnel, 1866, págs. 773, 789n.
^ Born & Wolf, 1970, pág. 40, eqs. (21a); Hecht, 2017, pág. 125, eqs. (4.42); Jenkins & White, 1976, pág. 524, eqs. (25a).
^ Fresnel, 1866, págs. 757, 789n.
^ Born & Wolf, 1970, pág. 40, eqs. (21a); Hecht, 2017, pág. 125, eqs. (4.43); Jenkins & White, 1976, pág. 524, eqs. (25a).
^ Whittaker, 1910, pág. 134; Darrigol, 2012, pág. 213 .
^ Stratton, 1941, p. 500, ecuación (44). La expresión correspondiente en Born & Wolf (1970, p. 50) es al revés, porque los términos representan argumentos en lugar de cambios de fase.
↑ Buchwald, 1989, págs. 394, 453 ; Fresnel, 1866, págs. 759, 786–7, 790.
^ PR Berman, 2012, "Efecto Goos-Hänchen", Scholarpedia 7 (3): 11584, § 2.1, especialmente las ecuaciones (1) a (3). Nótese que $la n$ de Berman es el recíproco de la $n$ del presente artículo.
^ ab Bliokh, KY; Aiello, A. (2013). "Desplazamientos del haz de Goos–Hänchen e Imbert–Fedorov: una descripción general". Journal of Optics . 15 (1): 014001. arXiv : 1210.8236 . Código Bibliográfico :2013JOpt...15a4001B. doi :10.1088/2040-8978/15/1/014001. S2CID 118380597.
^ Jenkins y White, 1976, págs. 40–42.
^ Rudd, WW (1971). "Colonoscopia con fibra óptica: un avance espectacular en la cirugía del colon". Canadian Family Physician . 17 (12): 42–45. PMC 2370306 . PMID 20468707.
^ Levitt, 2013, págs. 79–80.
^ Jenkins & White, 1976, págs. 26–7 (Porro, Dove, 90° Amici, reflector de esquina, Lummer-Brodhun); Born & Wolf, 1970, págs. 240–41 (Porro, Koenig), 243–4 (Dove).
^ Born & Wolf, 1970, pág. 241.
^ Born & Wolf, 1970, págs. 690–91.
^ R. Nave, "Prisms for Polarization" (Nicol, Glan–Foucault), Georgia State University, consultado el 27 de marzo de 2019; archivado el 25 de marzo de 2019.
^ Jenkins y White, 1976, págs. 510-11 (Nicol, Glan–Thompson, "Foucault").
^ JF Archard; AM Taylor (diciembre de 1948), "Prisma de Glan-Foucault mejorado", Journal of Scientific Instruments , 25 (12): 407–9, Bibcode :1948JScI...25..407A, doi :10.1088/0950-7671/25/12/304.
^ Buchwald, 1989, págs. 19-21; Jenkins y White, 1976, págs. 27-8.
^ ab "XII. Un método para examinar los poderes refractivos y dispersivos mediante reflexión prismática". Philosophical Transactions of the Royal Society of London . 92 : 365–380. 1802. doi :10.1098/rstl.1802.0014. S2CID 110328209.
^ HELLA GmbH & Co. KGaA, "Prueba del sensor de lluvia y del sensor de faros: instrucciones de reparación y diagnóstico de averías", consultado el 9 de abril de 2019; archivado el 8 de abril de 2019.
^ J. Gourlay, "Making Light Work – Light Sources for Modern Lighting Requirements", LED Professional , consultado el 29 de marzo de 2019; archivado el 12 de abril de 2016.
^ D. Axelrod (abril de 1981), "Contactos célula-sustrato iluminados por fluorescencia de reflexión interna total", Journal of Cell Biology , 89 (1): 141–5, doi :10.1083/jcb.89.1.141, PMC 2111781 , PMID 7014571 .
^ D. Axelrod (noviembre de 2001), "Microscopía de fluorescencia de reflexión interna total en biología celular" (PDF) , Traffic , 2 (11): 764–74, doi :10.1034/j.1600-0854.2001.21104.x, hdl : 2027.42/72779 , PMID 11733042, S2CID 15202097.
^ Hecht, 2017, pág. 138.
^ RW Astheimer; G. Falbel; S. Minkowitz (enero de 1966), "Modulación infrarroja mediante reflexión interna total frustrada", Applied Optics , 5 (1): 87–91, Bibcode :1966ApOpt...5...87A, doi :10.1364/AO.5.000087, PMID 20048791.
^ NJ Harrick (1962-3), "Huellas dactilares mediante reflexión interna total" ^{[ enlace muerto permanente ‍ ]} , Philips Technical Review , 24 (9): 271–4; archivado en enero de 2024
^ Noldus Information Technology, "CatWalk™ XT", consultado el 29 de marzo de 2019; archivado el 25 de marzo de 2019.
^ E. Bruce, R. Bendure, S. Krein y N. Lighthizer, "Acercarnos a la gonioscopia", Review of Optometry , 21 de septiembre de 2016.
^ Glaucoma Associates of Texas, "Gonioscopy", consultado el 29 de marzo de 2019; archivado el 22 de agosto de 2018.
^ Boyer, 1959, pág. 110.
^ Kamāl al-Dīn al-Fārisī, Tanqih al-Manazir (manuscrito autógrafo, 708 AH / 1309 CE ), Colección Adilnor.
^ Boyer, 1959, págs. 113, 114, 335. Boyer cita la edición de J. Würschmidt de De iride et radialibus Impressionibus de Teodorico , en Beiträge zur Geschichte der Philosophie des Mittelalters , vol. 12, núms. 5–6 (1914), en pág. 47.
^ Boyer, 1959, págs. 307, 335.
^ E. Mach (tr. ‍ JS Anderson y AFA Young), Los principios de la óptica física: un tratamiento histórico y filosófico (Londres: Methuen & Co, 1926), reimpreso en Mineola, NY: Dover, 2003, págs. 30-32.
^ AI Sabra, Teorías de la luz: de Descartes a Newton (Londres: Oldbourne Book Co., 1967), reimpreso en Cambridge University Press, 1981, págs. 111-12.
^ Huygens, 1690, trad. de Thompson, pág. 39.
^ Huygens, 1690, trad. Thompson, págs. 40-41. Nótese que la definición de Huygens del "ángulo de incidencia" es el complemento de la definición moderna.
^ Huygens, 1690, trad. de Thompson, págs. 39-40.
^ Huygens, 1690, trad. de Thompson, págs. 40-41.
^ Huygens, 1690, trad. de Thompson, págs. 16, 42.
^ Huygens, 1690, trad. de Thompson, págs. 92-4.
^ Newton, 1730, pág. 362.
^ Darrigol, 2012, págs. 93–4, 103.
^ Newton, 1730, págs. 370–71.
^ Newton, 1730, pág. 246. Nótese que un "seno" significaba la longitud de un lado para un "radio" específico (hipotenusa), mientras que hoy en día tomamos el radio como la unidad o expresamos el seno como una razón.
^ Newton, 1730, págs. 56–62, 264.
^ Newton, 1730, págs. 371–2.
^ Newton, 1730, pág. 281.
^ Newton, 1730, pág. 373.
^ Newton, 1730, pág. 356.
^ Buchwald, 1980, págs. 327, 331–2.
↑ Buchwald, 1980, págs. 335–6, 364; Buchwald, 1989, págs. 9–10, 13.
^ Buchwald, 1989, págs. 19-21.
^ Buchwald, 1989, pág. 28.
^ Darrigol, 2012, págs. 187–8.
^ Buchwald, 1989, pág. 30.
^ Buchwald, 1980, págs. 29-31.
^ E. Frankel (mayo de 1976), "Óptica corpuscular y la teoría ondulatoria de la luz: La ciencia y la política de una revolución en la física", Estudios Sociales de la Ciencia , 6 (2): 141–84, en la pág. 145.
↑ Cf. Buchwald, 1989, p. 30 (citando a Malus)
^ Darrigol, 2012, págs. 193–6, 290.
^ Darrigol, 2012, pág. 206.
^ Este efecto había sido descubierto previamente por Brewster , pero aún no había sido adecuadamente reportado. Véase: "Sobre una nueva especie de polarización móvil", [trimestral] Journal of Science and the Arts , vol. 2, núm. 3, 1817, pág. 213; T. Young , "Chromatics", Suplemento a las ediciones cuarta, quinta y sexta de la Encyclopædia Britannica , vol. 3 (primera mitad, publicado en febrero de 1818), pp. 141–63, en la pág. 157; Lloyd, 1834, pág. 368.
^ Darrigol, 2012, pág. 207.
^ A. Fresnel, "Mémoire sur les modifications que la réflexion imprime à la lumière polarisée" ("Memoria sobre las modificaciones que la reflexión imprime en la luz polarizada"), firmado y enviado el 10 de noviembre de 1817, leído el 24 de noviembre de 1817; impreso en Fresnel, 1866, pp. 441-485, incluidas las pp. 452 (redescubrimiento de la despolarización por reflexión interna total), 455 (dos reflexiones, "prismas acoplados", "paralelepípedo en vidrio"), 467-48 (diferencia de fase por reflexión); véase también la p. 487, nota 1, para la fecha de lectura.
^ Darrigol, 2012, pág. 212.
↑ Buchwald, 1989, págs. 390-391; Fresnel, 1866, págs. 646-68.
^ A. Fresnel, "Note sur le calcul des teintes que la polarization développe dans les lames cristallisées" et seq., Annales de Chimie et de Physique , Ser. 2, vol. 17, págs. 102–11 (mayo de 1821), 167–96 (junio de 1821), 312–15 ("Posdata", julio de 1821); reimpreso en Fresnel, 1866, págs. 609–48; traducido como "Sobre el cálculo de los tintes que desarrolla la polarización en placas cristalinas, y posdata", Zenodo : 4058004 , 2021.
^ ab A. Fresnel, "Mémoire sur la loi des modifications que la réflexion imprime à la lumière polarisée" ("Memoria sobre la ley de las modificaciones que la reflexión imprime a la luz polarizada"), leído el 7 de enero de 1823; reimpreso en Fresnel, 1866, pp. 767-799 (texto completo, publicado en 1831), pp. 753-762 (extracto, publicado en 1823). Véanse especialmente las pp. 773 (ley del seno), 757 (ley de la tangente), 760-761 y 792-76 (ángulos de reflexión interna total para diferencias de fase dadas).
^ Buchwald, 1989, págs. 391–3; Darrigol, 2012, págs. 212-13; Whittaker, 1910, págs. 133–5.
^ A. Fresnel, "Mémoire sur la double réfraction que les rayons lumineux éprouvent en traversant les aiguilles de cristal de roche suivant les Directions parallèles à l'axe", leído el 9 de diciembre de 1822; impreso en Fresnel, 1866, págs. 731–51 (texto completo), págs. 719–29 ( extrait , publicado por primera vez en Bulletin de la Société philomathique de 1822, págs. 191–8); texto completo traducido como "Memoria sobre la doble refracción que sufren los rayos de luz al atravesar las agujas de cuarzo en direcciones paralelas al eje", Zenodo : 4745976 , 2021.
↑ Buchwald, 1989, págs. 230-231; Fresnel, 1866, pág. 744.
↑ Lloyd, 1834, págs. 369–70; Buchwald, 1989, págs. 393–4, 453; Fresnel, 1866, págs. 781–96.
↑ Fresnel, 1866, págs. 760–61, 792–6; Whewell, 1857, pág. 359.
^ Fresnel, 1866, págs. 760–61, 792–3.
↑ Fresnel, 1866, págs. 761, 793–6; Whewell, 1857, pág. 359.
^ Bochner, 1963, págs. 198-200.
^ Whittaker, 1910, págs. 177–9.
^ Bochner, 1963, pág. 200; Born & Wolf, 1970, pág. 613.
^ Merriam-Webster, Inc., "critical angle", consultado el 21 de abril de 2019. (No se proporciona ninguna fuente primaria).
^ RP Feynman, 1985 (séptima impresión, 1988), QED: La extraña teoría de la luz y la materia , Princeton University Press, esp. págs. 33, 109–10.

Bibliografía

S. Bochner (junio de 1963), "La importancia de algunas concepciones matemáticas básicas para la física", Isis , 54 (2): 179–205; JSTOR 228537.
M. Born y E. Wolf, 1970, Principios de óptica , 4ª ed., Oxford: Pergamon Press.
CB Boyer, 1959, El arco iris: del mito a las matemáticas , Nueva York: Thomas Yoseloff.
JZ Buchwald (diciembre de 1980), "Investigaciones experimentales de la doble refracción desde Huygens hasta Malus", Archivo de Historia de las Ciencias Exactas , 21 (4): 311–373.
JZ Buchwald, 1989, El auge de la teoría ondulatoria de la luz: teoría óptica y experimentación a principios del siglo XIX , University of Chicago Press, ISBN 0-226-07886-8 .
O. Darrigol, 2012, Una historia de la óptica: desde la antigüedad griega hasta el siglo XIX , Oxford, ISBN 978-0-19-964437-7 .
R. Fitzpatrick, 2013, Oscilaciones y ondas: una introducción , Boca Raton, FL: CRC Press, ISBN 978-1-4665-6608-8 .
R. Fitzpatrick, 2013a, "Total Internal Reflection", Universidad de Texas en Austin, consultado el 14 de marzo de 2018.
A. Fresnel, 1866 (ed. H. de Senarmont, E. Verdet y L. Fresnel), Oeuvres complètes d'Augustin Fresnel , París: Imprimerie Impériale (3 vols., 1866-1870), vol. 1 (1866).
E. Hecht, 2017, Óptica , 5.ª ed., Pearson Education, ISBN 978-1-292-09693-3 .
C. Huygens, 1690, Traité de la Lumière (Leiden: Van der Aa), traducido por SP Thompson como Treatise on Light , University of Chicago Press, 1912; Proyecto Gutenberg, 2005. (Los números de página citados coinciden con la edición de 1912 y la edición HTML de Gutenberg).
FA Jenkins y HE White, 1976, Fundamentos de óptica , 4.ª ed., Nueva York: McGraw-Hill, ISBN 0-07-032330-5 .
TH Levitt, 2013, Un breve destello brillante: Augustin Fresnel y el nacimiento del faro moderno , Nueva York: WW Norton, ISBN 978-0-393-35089-0 .
H. Lloyd, 1834, "Informe sobre el progreso y el estado actual de la óptica física", Informe de la Cuarta Reunión de la Asociación Británica para el Avance de la Ciencia (celebrada en Edimburgo en 1834), Londres: J. Murray, 1835, págs. 295–413.
I. Newton, 1730, Opticks: or, a Treatise of the Reflections, Refractions, Inflections, and Colours of Light, 4.ª ed. (Londres: William Innys, 1730; Project Gutenberg, 2010); republicado con prólogo de A. Einstein e introducción de ET Whittaker (Londres: George Bell & Sons, 1931); reimpreso con prólogo adicional de IB Cohen y tabla analítica de contenidos de DHD Roller, Mineola, NY: Dover, 1952, 1979 (con prefacio revisado), 2012. (Los números de página citados coinciden con la edición HTML de Gutenberg y las ediciones de Dover).
HGJ Rutten y MAM van Venrooij, 1988 (quinta impresión, 2002), Óptica del telescopio: un manual completo para astrónomos aficionados , Richmond, VA: Willmann-Bell, ISBN 978-0-943396-18-7 .
JA Stratton, 1941, Teoría electromagnética , Nueva York: McGraw-Hill.
W. Whewell, 1857, Historia de las ciencias inductivas: desde los primeros tiempos hasta la actualidad , 3.ª ed., Londres: JW Parker & Son, vol. 2.
ET Whittaker , 1910, [https://archive.org/details/historyoftheorie00whitrich Una historia de las teorías del éter y la electricidad: desde la era de Descartes hasta finales del siglo XIX , Londres: Longmans, Green, & Co.

Enlaces externos

Wikimedia Commons tiene medios relacionados con Reflexión interna total.

Sr. Mangiacapre, "Fluorescencia en un líquido" (video, 1m ‍ 28s ), subido el 13 de marzo de 2012. (Fluorescencia y TIR de un rayo láser violeta en agua de quinina.)
PhysicsatUVM, "Reflexión interna total frustrada" (video, 37 s), subido el 21 de noviembre de 2011. ("Un rayo láser sufre una reflexión interna total en un trozo de plexiglás empañado...")
SMUPhysics, "Reflexión interna" (video, 12 s), subido el 20 de mayo de 2010. (Transición desde la refracción a través del ángulo crítico hasta la TIR en un prisma de 45°-90°-45°.)