función theta

Funciones especiales de varias variables complejas.

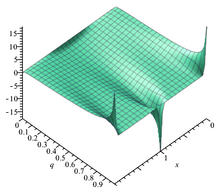
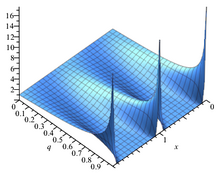
Función theta de Jacobi θ ₁ con nomo q = e ^{i π τ} = 0,1 e ^{0,1 i π} : ${\displaystyle {\begin{aligned}\theta _{1}(z,q)&=2q^{\frac {1}{4}}\sum _{n=0}^{\infty }(-1)^{n}q^{n(n+1)}\sin(2n+1)z\\&=\sum _{n=-\infty }^{\infty }(-1)^{n-{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}e^{(2n+1)iz}.\end{aligned}}}$

En matemáticas , las funciones theta son funciones especiales de varias variables complejas . Aparecen en muchos temas, incluidas variedades abelianas , espacios de módulos , formas cuadráticas y solitones . Como álgebras de Grassmann , aparecen en la teoría cuántica de campos . ^[1]

La forma más común de función theta es la que ocurre en la teoría de funciones elípticas . Con respecto a una de las variables complejas (convencionalmente llamada z ), una función theta tiene una propiedad que expresa su comportamiento con respecto a la suma de un período de las funciones elípticas asociadas, lo que la convierte en una función cuasiperiódica . En la teoría abstracta, esta cuasiperiodicidad proviene de la clase de cohomología de un haz de líneas sobre un toro complejo , una condición de descenso .

Una interpretación de las funciones theta cuando se trata de la ecuación del calor es que "una función theta es una función especial que describe la evolución de la temperatura en un dominio de segmento sujeto a ciertas condiciones de contorno". ^[2]

A lo largo de este artículo, deberá interpretarse como (con el fin de resolver cuestiones de elección de sucursal ). ^{[nota 1]} ${\displaystyle (e^{\pi i\tau })^{\alpha }}$ ${\displaystyle e^{\alpha \pi i\tau }}$

Función theta de Jacobi

Hay varias funciones estrechamente relacionadas llamadas funciones theta de Jacobi y muchos sistemas de notación diferentes e incompatibles para ellas. Una función theta de Jacobi (llamada así en honor a Carl Gustav Jacob Jacobi ) es una función definida para dos variables complejas z y τ , donde z puede ser cualquier número complejo y τ es la relación de medio período , confinada al semiplano superior , lo que significa tiene parte imaginaria positiva. Está dada por la fórmula

${\displaystyle {\begin{aligned}\vartheta (z;\tau )&=\sum _{n=-\infty }^{\infty }\exp \left(\pi in^{2}\tau +2\pi inz\right)\\&=1+2\sum _{n=1}^{\infty }q^{n^{2}}\cos(2\pi nz)\\&=\sum _{n=-\infty }^{\infty }q^{n^{2}}\eta ^{n}\end{aligned}}}$

donde q = exp( πiτ ) es el nomo y η = exp(2 πiz ) . Es una forma Jacobi . La restricción asegura que se trata de una serie absolutamente convergente. En τ fijo , esta es una serie de Fourier para una función entera 1 periódica de z . En consecuencia, la función theta es 1-periódica en z :

${\displaystyle \vartheta (z+1;\tau )=\vartheta (z;\tau ).}$

Al completar el cuadrado , también es τ -cuasiperiódico en z , con

${\displaystyle \vartheta (z+\tau ;\tau )=\exp {\bigl (}-\pi i(\tau +2z){\bigr )}\vartheta (z;\tau ).}$

Así, en general,

${\displaystyle \vartheta (z+a+b\tau ;\tau )=\exp \left(-\pi ib^{2}\tau -2\pi ibz\right)\vartheta (z;\tau )}$

para cualquier número entero a y b .

Para cualquier fijo , la función es una función completa en el plano complejo, por lo que, según el teorema de Liouville , no puede ser doblemente periódica a menos que sea constante, por lo que lo mejor que podemos hacer es hacerla periódica y cuasi periódica . De hecho, desde y , la función es ilimitada, como lo exige el teorema de Liouville. ${\displaystyle \tau }$ ${\displaystyle 1,\tau }$ ${\displaystyle 1}$ ${\displaystyle \tau }$ $${\displaystyle \left|{\frac {\vartheta (z+a+b\tau ;\tau )}{\vartheta (z;\tau )}}\right|=\exp \left(\pi (b^{2}\Im (\tau )+2b\Im (z))\right)}$$ ${\displaystyle \Im (\tau )>0}$ ${\displaystyle \vartheta (z,\tau )}$

De hecho, es la función completa más general con 2 cuasiperíodos, en el siguiente sentido: ^[3]

Teorema  :  If es completo y no constante, y satisface las ecuaciones funcionales para alguna constante . ${\displaystyle f:\mathbb {C} \to \mathbb {C} }$ ${\displaystyle {\begin{cases}f(z+1)=f(z)\\f(z+\tau )=e^{az+2\pi ib}f(z)\end{cases}}}$ ${\displaystyle a,b\in \mathbb {C} }$

Si , entonces y . Si , entonces para algún valor distinto de cero . ${\displaystyle a=0}$ ${\displaystyle b=\tau }$ ${\displaystyle f(z)=e^{2\pi iz}}$ ${\displaystyle a=-2\pi i}$ ${\displaystyle f(z)=C\vartheta (z+{\frac {1}{2}}\tau +b,\tau )}$ ${\displaystyle C\in \mathbb {C} }$

Función theta θ ₁ con diferente nombre q = e ^iπτ . El punto negro en la imagen de la derecha indica cómo q cambia con τ .

Función theta θ ₁ con diferente nombre q = e ^iπτ . El punto negro en la imagen de la derecha indica cómo q cambia con τ .

Funciones auxiliares

La función theta de Jacobi definida anteriormente a veces se considera junto con tres funciones theta auxiliares, en cuyo caso se escribe con un subíndice doble 0:

${\displaystyle \vartheta _{00}(z;\tau )=\vartheta (z;\tau )}$

Las funciones auxiliares (o de medio período) están definidas por

${\displaystyle {\begin{aligned}\vartheta _{01}(z;\tau )&=\vartheta \left(z+{\tfrac {1}{2}};\tau \right)\\[3pt]\vartheta _{10}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi iz\right)\vartheta \left(z+{\tfrac {1}{2}}\tau ;\tau \right)\\[3pt]\vartheta _{11}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi i\left(z+{\tfrac {1}{2}}\right)\right)\vartheta \left(z+{\tfrac {1}{2}}\tau +{\tfrac {1}{2}};\tau \right).\end{aligned}}}$

Esta notación sigue a Riemann y Mumford ; La formulación original de Jacobi estaba en términos del nomo q = e ^iπτ en lugar de τ . En la notación de Jacobi, las funciones θ se escriben:

${\displaystyle {\begin{aligned}\theta _{1}(z;q)&=\theta _{1}(\pi z,q)=-\vartheta _{11}(z;\tau )\\\theta _{2}(z;q)&=\theta _{2}(\pi z,q)=\vartheta _{10}(z;\tau )\\\theta _{3}(z;q)&=\theta _{3}(\pi z,q)=\vartheta _{00}(z;\tau )\\\theta _{4}(z;q)&=\theta _{4}(\pi z,q)=\vartheta _{01}(z;\tau )\end{aligned}}}$

Jacobi theta 1

Jacobi theta 2

Jacobi theta 3

Jacobi theta 4

Las definiciones anteriores de las funciones theta de Jacobi no son de ninguna manera únicas. Consulte Funciones theta de Jacobi (variaciones de notación) para obtener más información.

Si establecemos z = 0 en las funciones theta anteriores, obtenemos cuatro funciones de τ únicamente, definidas en el semiplano superior. Estas funciones se denominan funciones Theta Nullwert , basadas en el término alemán para valor cero debido a la anulación de la entrada izquierda en la expresión de la función theta. Alternativamente, obtenemos cuatro funciones de q únicamente, definidas en el disco unitario . A veces se les llama constantes theta : ^{[nota 2]} ${\displaystyle |q|<1}$

${\displaystyle {\begin{aligned}\vartheta _{11}(0;\tau )&=-\theta _{1}(q)=-\sum _{n=-\infty }^{\infty }(-1)^{n-1/2}q^{(n+1/2)^{2}}\\\vartheta _{10}(0;\tau )&=\theta _{2}(q)=\sum _{n=-\infty }^{\infty }q^{(n+1/2)^{2}}\\\vartheta _{00}(0;\tau )&=\theta _{3}(q)=\sum _{n=-\infty }^{\infty }q^{n^{2}}\\\vartheta _{01}(0;\tau )&=\theta _{4}(q)=\sum _{n=-\infty }^{\infty }(-1)^{n}q^{n^{2}}\end{aligned}}}$

con el nombre q = e ^iπτ . Observa eso . Estos se pueden utilizar para definir una variedad de formas modulares y para parametrizar ciertas curvas; en particular, la identidad Jacobi es ${\displaystyle \theta _{1}(q)=0}$

${\displaystyle \theta _{2}(q)^{4}+\theta _{4}(q)^{4}=\theta _{3}(q)^{4}}$

o equivalente,

${\displaystyle \vartheta _{01}(0;\tau )^{4}+\vartheta _{10}(0;\tau )^{4}=\vartheta _{00}(0;\tau )^{4}}$

que es la curva de Fermat de grado cuatro.

identidades jacobi

Las identidades de Jacobi describen cómo las funciones theta se transforman bajo el grupo modular , que se genera por τ ↦ τ + 1 y τ ↦ − ⁠1/τ⁠ . Las ecuaciones para la primera transformada se encuentran fácilmente ya que sumar uno a τ en el exponente tiene el mismo efecto que sumar ⁠1/2⁠ a z ( n ≡ n ² mod 2 ). Para el segundo, deja

${\displaystyle \alpha =(-i\tau )^{\frac {1}{2}}\exp \left({\frac {\pi }{\tau }}iz^{2}\right).}$

Entonces

${\displaystyle {\begin{aligned}\vartheta _{00}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{00}(z;\tau )\quad &\vartheta _{01}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{10}(z;\tau )\\[3pt]\vartheta _{10}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{01}(z;\tau )\quad &\vartheta _{11}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=-i\alpha \,\vartheta _{11}(z;\tau ).\end{aligned}}}$

Funciones theta en términos del nomo

En lugar de expresar las funciones Theta en términos de z y τ , podemos expresarlas en términos de argumentos w y el nombre q , donde w = e ^πiz y q = e ^πiτ . De esta forma, las funciones se convierten

${\displaystyle {\begin{aligned}\vartheta _{00}(w,q)&=\sum _{n=-\infty }^{\infty }\left(w^{2}\right)^{n}q^{n^{2}}\quad &\vartheta _{01}(w,q)&=\sum _{n=-\infty }^{\infty }(-1)^{n}\left(w^{2}\right)^{n}q^{n^{2}}\\[3pt]\vartheta _{10}(w,q)&=\sum _{n=-\infty }^{\infty }\left(w^{2}\right)^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}\quad &\vartheta _{11}(w,q)&=i\sum _{n=-\infty }^{\infty }(-1)^{n}\left(w^{2}\right)^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}.\end{aligned}}}$

Vemos que las funciones theta también se pueden definir en términos de w y q , sin una referencia directa a la función exponencial. Por lo tanto, estas fórmulas se pueden utilizar para definir las funciones Theta sobre otros campos donde la función exponencial podría no estar definida en todas partes, como los campos de números p -ádicos .

Representaciones de productos

El triple producto de Jacobi (un caso especial de las identidades de Macdonald ) nos dice que para números complejos w y q con | q | < 1 y w ≠ 0 tenemos

${\displaystyle \prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+w^{2}q^{2m-1}\right)\left(1+w^{-2}q^{2m-1}\right)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.}$

Puede demostrarse por medios elementales, como por ejemplo en Introducción a la teoría de números de Hardy y Wright .

Si expresamos la función theta en términos del nombre q = e ^πiτ (observando que algunos autores establecen q = e ^{2 πiτ} ) y tomamos w = e ^πiz entonces

${\displaystyle \vartheta (z;\tau )=\sum _{n=-\infty }^{\infty }\exp(\pi i\tau n^{2})\exp(2\pi izn)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.}$

Por lo tanto obtenemos una fórmula de producto para la función theta en la forma

${\displaystyle \vartheta (z;\tau )=\prod _{m=1}^{\infty }{\big (}1-\exp(2m\pi i\tau ){\big )}{\Big (}1+\exp {\big (}(2m-1)\pi i\tau +2\pi iz{\big )}{\Big )}{\Big (}1+\exp {\big (}(2m-1)\pi i\tau -2\pi iz{\big )}{\Big )}.}$

En términos de w y q :

${\displaystyle {\begin{aligned}\vartheta (z;\tau )&=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+q^{2m-1}w^{2}\right)\left(1+{\frac {q^{2m-1}}{w^{2}}}\right)\\&=\left(q^{2};q^{2}\right)_{\infty }\,\left(-w^{2}q;q^{2}\right)_{\infty }\,\left(-{\frac {q}{w^{2}}};q^{2}\right)_{\infty }\\&=\left(q^{2};q^{2}\right)_{\infty }\,\theta \left(-w^{2}q;q^{2}\right)\end{aligned}}}$

donde ( ; ) _∞ es el símbolo q -Pochhammer y θ ( ; ) es la función q -theta . Ampliando los términos, el triple producto de Jacobi también se puede escribir

${\displaystyle \prod _{m=1}^{\infty }\left(1-q^{2m}\right){\Big (}1+\left(w^{2}+w^{-2}\right)q^{2m-1}+q^{4m-2}{\Big )},}$

que también podemos escribir como

${\displaystyle \vartheta (z\mid q)=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right).}$

Esta forma es válida en general pero claramente es de particular interés cuando z es real. Fórmulas de productos similares para las funciones theta auxiliares son

${\displaystyle {\begin{aligned}\vartheta _{01}(z\mid q)&=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right),\\[3pt]\vartheta _{10}(z\mid q)&=2q^{\frac {1}{4}}\cos(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m}+q^{4m}\right),\\[3pt]\vartheta _{11}(z\mid q)&=-2q^{\frac {1}{4}}\sin(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m}+q^{4m}\right).\end{aligned}}}$

En particular, podemos interpretarlas como deformaciones de un parámetro de las funciones periódicas , validando nuevamente la interpretación de la función theta como la función de 2 cuasi períodos más general. $${\displaystyle \lim _{q\to 0}{\frac {\vartheta _{10}(z\mid q)}{2q^{\frac {1}{4}}}}=\cos(\pi z),\quad \lim _{q\to 0}{\frac {-\vartheta _{11}(z\mid q)}{2q^{-{\frac {1}{4}}}}}=\sin(\pi z)}$$ ${\displaystyle \sin ,\cos }$

Representaciones integrales

Las funciones theta de Jacobi tienen las siguientes representaciones integrales:

${\displaystyle {\begin{aligned}\vartheta _{00}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi u)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{01}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{10}(z;\tau )&=-ie^{i\pi z+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi u+\pi \tau u)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{11}(z;\tau )&=e^{i\pi z+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi \tau u)}{\sin(\pi u)}}\mathrm {d} u.\end{aligned}}}$

Theta Nullwert funciona como esta identidad integral: ${\displaystyle \theta _{3}(q)}$

${\displaystyle \theta _{3}(q)=1+{\frac {4q{\sqrt {\ln(1/q)}}}{\sqrt {\pi }}}\int _{0}^{\infty }{\frac {\exp[-\ln(1/q)\,x^{2}]\{1-q^{2}\cos[2\ln(1/q)\,x]\}}{1-2q^{2}\cos[2\ln(1/q)\,x]+q^{4}}}\,\mathrm {d} x}$

Esta fórmula fue analizada en el ensayo Serie Square que genera transformaciones de funciones del matemático Maxie Schmidt de Georgia en Atlanta.

Sobre la base de esta fórmula se dan los siguientes tres ejemplos eminentes:

${\displaystyle {\biggl [}{\frac {2}{\pi }}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}{\biggr ]}^{1/2}=\theta _{3}{\bigl [}\exp(-\pi ){\bigr ]}=1+4\exp(-\pi )\int _{0}^{\infty }{\frac {\exp(-\pi x^{2})[1-\exp(-2\pi )\cos(2\pi x)]}{1-2\exp(-2\pi )\cos(2\pi x)+\exp(-4\pi )}}\,\mathrm {d} x}$

${\displaystyle {\biggl [}{\frac {2}{\pi }}K({\sqrt {2}}-1){\biggr ]}^{1/2}=\theta _{3}{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=1+4\,{\sqrt[{4}]{2}}\exp(-{\sqrt {2}}\,\pi )\int _{0}^{\infty }{\frac {\exp(-{\sqrt {2}}\,\pi x^{2})[1-\exp(-2{\sqrt {2}}\,\pi )\cos(2{\sqrt {2}}\,\pi x)]}{1-2\exp(-2{\sqrt {2}}\,\pi )\cos(2{\sqrt {2}}\,\pi x)+\exp(-4{\sqrt {2}}\,\pi )}}\,\mathrm {d} x}$

${\displaystyle {\biggl \{}{\frac {2}{\pi }}K{\bigl [}\sin {\bigl (}{\frac {\pi }{12}}{\bigr )}{\bigr ]}{\biggr \}}^{1/2}=\theta _{3}{\bigl [}\exp(-{\sqrt {3}}\,\pi ){\bigr ]}=1+4\,{\sqrt[{4}]{3}}\exp(-{\sqrt {3}}\,\pi )\int _{0}^{\infty }{\frac {\exp(-{\sqrt {3}}\,\pi x^{2})[1-\exp(-2{\sqrt {3}}\,\pi )\cos(2{\sqrt {3}}\,\pi x)]}{1-2\exp(-2{\sqrt {3}}\,\pi )\cos(2{\sqrt {3}}\,\pi x)+\exp(-4{\sqrt {3}}\,\pi )}}\,\mathrm {d} x}$

Además, se mostrarán los ejemplos theta y : ${\displaystyle \theta _{3}({\tfrac {1}{2}})}$ ${\displaystyle \theta _{3}({\tfrac {1}{3}})}$

${\displaystyle \theta _{3}{\bigl (}{\frac {1}{2}}{\bigr )}=1+2\sum _{n=1}^{\infty }{\frac {1}{2^{n^{2}}}}=1+2\pi ^{-1/2}{\sqrt {\ln(2)}}\int _{0}^{\infty }{\frac {\exp[-\ln(2)\,x^{2}]\{16-4\cos[2\ln(2)\,x]\}}{17-8\cos[2\ln(2)\,x]}}\,\mathrm {d} x}$

${\displaystyle \theta _{3}{\bigl (}{\frac {1}{2}}{\bigr )}=2.128936827211877158669\ldots }$

${\displaystyle \theta _{3}{\bigl (}{\frac {1}{3}}{\bigr )}=1+2\sum _{n=1}^{\infty }{\frac {1}{3^{n^{2}}}}=1+{\frac {4}{3}}\pi ^{-1/2}{\sqrt {\ln(3)}}\int _{0}^{\infty }{\frac {\exp[-\ln(3)\,x^{2}]\{81-9\cos[2\ln(3)\,x]\}}{82-18\cos[2\ln(3)\,x]}}\,\mathrm {d} x}$

${\displaystyle \theta _{3}{\bigl (}{\frac {1}{3}}{\bigr )}=1.691459681681715341348\ldots }$

Valores explícitos

Valores lemniscaticos

El mérito de la mayoría de estos resultados es para Ramanujan. Véase el cuaderno perdido de Ramanujan y una referencia relevante en la función de Euler . Los resultados de Ramanujan citados en la función de Euler más algunas operaciones elementales dan los resultados a continuación, por lo que están en el cuaderno perdido de Ramanujan o se derivan inmediatamente de él. Véase también Yi (2004). ^[4] Definir,

${\displaystyle \quad \varphi (q)=\vartheta _{00}(0;\tau )=\theta _{3}(0;q)=\sum _{n=-\infty }^{\infty }q^{n^{2}}}$

con el nombre y la función Dedekind eta Entonces para ${\displaystyle q=e^{\pi i\tau },}$ ${\displaystyle \tau =n{\sqrt {-1}},}$ ${\displaystyle \eta (\tau ).}$ ${\displaystyle n=1,2,3,\dots }$

${\displaystyle {\begin{aligned}\varphi \left(e^{-\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}={\sqrt {2}}\,\eta \left({\sqrt {-1}}\right)\\\varphi \left(e^{-2\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {2+{\sqrt {2}}}}{2}}\\\varphi \left(e^{-3\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {1+{\sqrt {3}}}}{\sqrt[{8}]{108}}}\\\varphi \left(e^{-4\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {2+{\sqrt[{4}]{8}}}{4}}\\\varphi \left(e^{-5\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt {\frac {2+{\sqrt {5}}}{5}}}\\\varphi \left(e^{-6\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{1}}+{\sqrt[{4}]{3}}+{\sqrt[{4}]{4}}+{\sqrt[{4}]{9}}}}{\sqrt[{8}]{12^{3}}}}\\\varphi \left(e^{-7\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt {13+{\sqrt {7}}}}+{\sqrt {7+3{\sqrt {7}}}}}}{{\sqrt[{8}]{14^{3}}}\cdot {\sqrt[{16}]{7}}}}\\\varphi \left(e^{-8\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {{\sqrt {2+{\sqrt {2}}}}+{\sqrt[{8}]{128}}}{4}}\\\varphi \left(e^{-9\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {1+{\sqrt[{3}]{2+2{\sqrt {3}}}}}{3}}\\\varphi \left(e^{-10\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{64}}+{\sqrt[{4}]{80}}+{\sqrt[{4}]{81}}+{\sqrt[{4}]{100}}}}{\sqrt[{4}]{200}}}\\\varphi \left(e^{-11\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {11+{\sqrt {11}}+(5+3{\sqrt {3}}+{\sqrt {11}}+{\sqrt {33}}){\sqrt[{3}]{-44+33{\sqrt {3}}}}+(-5+3{\sqrt {3}}-{\sqrt {11}}+{\sqrt {33}}){\sqrt[{3}]{44+33{\sqrt {3}}}}}}{\sqrt[{8}]{52180524}}}\\\varphi \left(e^{-12\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{1}}+{\sqrt[{4}]{2}}+{\sqrt[{4}]{3}}+{\sqrt[{4}]{4}}+{\sqrt[{4}]{9}}+{\sqrt[{4}]{18}}+{\sqrt[{4}]{24}}}}{2{\sqrt[{8}]{108}}}}\\\varphi \left(e^{-13\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {13+8{\sqrt {13}}+(11-6{\sqrt {3}}+{\sqrt {13}}){\sqrt[{3}]{143+78{\sqrt {3}}}}+(11+6{\sqrt {3}}+{\sqrt {13}}){\sqrt[{3}]{143-78{\sqrt {3}}}}}}{\sqrt[{4}]{19773}}}\\\varphi \left(e^{-14\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt {13+{\sqrt {7}}}}+{\sqrt {7+3{\sqrt {7}}}}+{\sqrt {10+2{\sqrt {7}}}}+{\sqrt[{8}]{28}}{\sqrt {4+{\sqrt {7}}}}}}{\sqrt[{16}]{28^{7}}}}\\\varphi \left(e^{-15\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {7+3{\sqrt {3}}+{\sqrt {5}}+{\sqrt {15}}+{\sqrt[{4}]{60}}+{\sqrt[{4}]{1500}}}}{{\sqrt[{8}]{12^{3}}}\cdot {\sqrt {5}}}}\\2\varphi \left(e^{-16\pi }\right)&=\varphi \left(e^{-4\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt[{4}]{1+{\sqrt {2}}}}{\sqrt[{16}]{128}}}\\\varphi \left(e^{-17\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {{\sqrt {2}}(1+{\sqrt[{4}]{17}})+{\sqrt[{8}]{17}}{\sqrt {5+{\sqrt {17}}}}}{\sqrt {17+17{\sqrt {17}}}}}\\2\varphi \left(e^{-20\pi }\right)&=\varphi \left(e^{-5\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt {\frac {3+2{\sqrt[{4}]{5}}}{5{\sqrt {2}}}}}\\6\varphi \left(e^{-36\pi }\right)&=3\varphi \left(e^{-9\pi }\right)+2\varphi \left(e^{-4\pi }\right)-\varphi \left(e^{-\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt[{3}]{{\sqrt[{4}]{2}}+{\sqrt[{4}]{18}}+{\sqrt[{4}]{216}}}}\end{aligned}}}$

Si el recíproco de la constante de Gelfond se eleva a la potencia del recíproco de un número impar, entonces los valores o valores correspondientes se pueden representar de forma simplificada utilizando el seno lemniscático hiperbólico : ${\displaystyle \vartheta _{00}}$ ${\displaystyle \phi }$

${\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{5}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{5}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{5}}{\sqrt {2}}\,\varpi {\bigr )}}$

${\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{7}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{7}}{\sqrt {2}}\,\varpi {\bigr )}}$

${\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{9}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{9}}{\sqrt {2}}\,\varpi {\bigr )}}$

${\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{11}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {5}{11}}{\sqrt {2}}\,\varpi {\bigr )}}$

Con la letra se representa la constante Lemniscata . ${\displaystyle \varpi }$

Tenga en cuenta que se mantienen las siguientes identidades modulares:

${\displaystyle {\begin{aligned}2\varphi \left(q^{4}\right)&=\varphi (q)+{\sqrt {2\varphi ^{2}\left(q^{2}\right)-\varphi ^{2}(q)}}\\3\varphi \left(q^{9}\right)&=\varphi (q)+{\sqrt[{3}]{9{\frac {\varphi ^{4}\left(q^{3}\right)}{\varphi (q)}}-\varphi ^{3}(q)}}\\{\sqrt {5}}\varphi \left(q^{25}\right)&=\varphi \left(q^{5}\right)\cot \left({\frac {1}{2}}\arctan \left({\frac {2}{\sqrt {5}}}{\frac {\varphi (q)\varphi \left(q^{5}\right)}{\varphi ^{2}(q)-\varphi ^{2}\left(q^{5}\right)}}{\frac {1+s(q)-s^{2}(q)}{s(q)}}\right)\right)\end{aligned}}}$

¿Dónde está la fracción continua de Rogers-Ramanujan ? ${\displaystyle s(q)=s\left(e^{\pi i\tau }\right)=-R\left(-e^{-\pi i/(5\tau )}\right)}$

${\displaystyle {\begin{aligned}s(q)&={\sqrt[{5}]{\tan \left({\frac {1}{2}}\arctan \left({\frac {5}{2}}{\frac {\varphi ^{2}\left(q^{5}\right)}{\varphi ^{2}(q)}}-{\frac {1}{2}}\right)\right)\cot ^{2}\left({\frac {1}{2}}\operatorname {arccot} \left({\frac {5}{2}}{\frac {\varphi ^{2}\left(q^{5}\right)}{\varphi ^{2}(q)}}-{\frac {1}{2}}\right)\right)}}\\&={\cfrac {e^{-\pi i/(25\tau )}}{1-{\cfrac {e^{-\pi i/(5\tau )}}{1+{\cfrac {e^{-2\pi i/(5\tau )}}{1-\ddots }}}}}}\end{aligned}}}$

Equianarmónicovalores

El matemático Bruce Berndt descubrió otros valores ^[5] de la función theta:

${\displaystyle {\begin{array}{lll}\varphi \left(\exp(-{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{13/8}\\\varphi \left(\exp(-2{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{13/8}\cos({\tfrac {1}{24}}\pi )\\\varphi \left(\exp(-3{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{7/8}({\sqrt[{3}]{2}}+1)\\\varphi \left(\exp(-4{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-5/3}3^{13/8}{\Bigl (}1+{\sqrt {\cos({\tfrac {1}{12}}\pi )}}{\Bigr )}\\\varphi \left(\exp(-5{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{5/8}\sin({\tfrac {1}{5}}\pi )({\tfrac {2}{5}}{\sqrt[{3}]{100}}+{\tfrac {2}{5}}{\sqrt[{3}]{10}}+{\tfrac {3}{5}}{\sqrt {5}}+1)\end{array}}}$

Otros valores

Muchos valores de la función theta ^[6] y especialmente de la función phi mostrada se pueden representar en términos de la función gamma:

${\displaystyle {\begin{array}{lll}\varphi \left(\exp(-{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{7/8}\\\varphi \left(\exp(-2{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{1/8}{\Bigl (}1+{\sqrt {{\sqrt {2}}-1}}{\Bigr )}\\\varphi \left(\exp(-3{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{3/8}3^{-1/2}({\sqrt {3}}+1){\sqrt {\tan({\tfrac {5}{24}}\pi )}}\\\varphi \left(\exp(-4{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{-1/8}{\Bigl (}1+{\sqrt[{4}]{2{\sqrt {2}}-2}}{\Bigr )}\\\varphi \left(\exp(-5{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}{\frac {1}{15}}\,2^{3/8}\times \\&&\times {\biggl [}{\sqrt[{3}]{5}}\,{\sqrt {10+2{\sqrt {5}}}}{\biggl (}{\sqrt[{3}]{5+{\sqrt {2}}+3{\sqrt {3}}}}+{\sqrt[{3}]{5+{\sqrt {2}}-3{\sqrt {3}}}}\,{\biggr )}-{\bigl (}2-{\sqrt {2}}\,{\bigr )}{\sqrt {25-10{\sqrt {5}}}}\,{\biggr ]}\\\varphi \left(\exp(-{\sqrt {6}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {5}{24}}\right){\Gamma \left({\tfrac {5}{12}}\right)}^{-1/2}2^{-13/24}3^{-1/8}{\sqrt {\sin({\tfrac {5}{12}}\pi )}}\\\varphi \left(\exp(-{\tfrac {1}{2}}{\sqrt {6}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {5}{24}}\right){\Gamma \left({\tfrac {5}{12}}\right)}^{-1/2}2^{5/24}3^{-1/8}\sin({\tfrac {5}{24}}\pi )\end{array}}}$

Teoremas de potencia de Nome

Teoremas de potencia directa

Para la transformación del nomo ^[7] en las funciones theta se pueden utilizar estas fórmulas:

${\displaystyle \theta _{2}(q^{2})={\tfrac {1}{2}}{\sqrt {2[\theta _{3}(q)^{2}-\theta _{4}(q)^{2}]}}}$

${\displaystyle \theta _{3}(q^{2})={\tfrac {1}{2}}{\sqrt {2[\theta _{3}(q)^{2}+\theta _{4}(q)^{2}]}}}$

${\displaystyle \theta _{4}(q^{2})={\sqrt {\theta _{4}(q)\theta _{3}(q)}}}$

Los cuadrados de las tres funciones theta de valor cero con la función cuadrada como función interna también se forman en el patrón de los triples pitagóricos según la identidad de Jacobi. Además, esas transformaciones son válidas:

${\displaystyle \theta _{3}(q^{4})={\tfrac {1}{2}}\theta _{3}(q)+{\tfrac {1}{2}}\theta _{4}(q)}$

Estas fórmulas se pueden utilizar para calcular los valores theta del cubo del nomo:

${\displaystyle 27\,\theta _{3}(q^{3})^{8}-18\,\theta _{3}(q^{3})^{4}\theta _{3}(q)^{4}-\,\theta _{3}(q)^{8}=8\,\theta _{3}(q^{3})^{2}\theta _{3}(q)^{2}[2\,\theta _{4}(q)^{4}-\theta _{3}(q)^{4}]}$

${\displaystyle 27\,\theta _{4}(q^{3})^{8}-18\,\theta _{4}(q^{3})^{4}\theta _{4}(q)^{4}-\,\theta _{4}(q)^{8}=8\,\theta _{4}(q^{3})^{2}\theta _{4}(q)^{2}[2\,\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]}$

Y se pueden utilizar las siguientes fórmulas para calcular los valores theta de la quinta potencia del nomo:

${\displaystyle [\theta _{3}(q)^{2}-\theta _{3}(q^{5})^{2}][5\,\theta _{3}(q^{5})^{2}-\theta _{3}(q)^{2}]^{5}=256\,\theta _{3}(q^{5})^{2}\theta _{3}(q)^{2}\theta _{4}(q)^{4}[\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]}$

${\displaystyle [\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}][5\,\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}]^{5}=256\,\theta _{4}(q^{5})^{2}\theta _{4}(q)^{2}\theta _{3}(q)^{4}[\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]}$

Transformación en la raíz cúbica del nomo.

Las fórmulas para los valores de la función theta Nullwert a partir de la raíz cúbica del nomo elíptico se obtienen contrastando las dos soluciones reales de las ecuaciones cuárticas correspondientes:

${\displaystyle {\biggl [}{\frac {\theta _{3}(q^{1/3})^{2}}{\theta _{3}(q)^{2}}}-{\frac {3\,\theta _{3}(q^{3})^{2}}{\theta _{3}(q)^{2}}}{\biggr ]}^{2}=4-4{\biggl [}{\frac {2\,\theta _{2}(q)^{2}\theta _{4}(q)^{2}}{\theta _{3}(q)^{4}}}{\biggr ]}^{2/3}}$

${\displaystyle {\biggl [}{\frac {3\,\theta _{4}(q^{3})^{2}}{\theta _{4}(q)^{2}}}-{\frac {\theta _{4}(q^{1/3})^{2}}{\theta _{4}(q)^{2}}}{\biggr ]}^{2}=4+4{\biggl [}{\frac {2\,\theta _{2}(q)^{2}\theta _{3}(q)^{2}}{\theta _{4}(q)^{4}}}{\biggr ]}^{2/3}}$

Transformación en la quinta raíz del nomo.

La fracción continua de Rogers-Ramanujan se puede definir en términos de la función theta de Jacobi de la siguiente manera:

${\displaystyle R(q)=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}}$

${\displaystyle R(q^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}}$

${\displaystyle R(q^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}}$

La función de fracción continua alterna de Rogers-Ramanujan S (q) tiene las dos identidades siguientes:

${\displaystyle S(q)={\frac {R(q^{4})}{R(q^{2})R(q)}}=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}}$

Los valores de la función theta de la quinta raíz del nomo se pueden representar como una combinación racional de las fracciones continuas R y S y los valores de la función theta de la quinta potencia del nomo y el nomo mismo. Las siguientes cuatro ecuaciones son válidas para todos los valores q entre 0 y 1:

${\displaystyle {\frac {\theta _{3}(q^{1/5})}{\theta _{3}(q^{5})}}-1={\frac {1}{S(q)}}{\bigl [}S(q)^{2}+R(q^{2}){\bigr ]}{\bigl [}1+R(q^{2})S(q){\bigr ]}}$

${\displaystyle 1-{\frac {\theta _{4}(q^{1/5})}{\theta _{4}(q^{5})}}={\frac {1}{R(q)}}{\bigl [}R(q^{2})+R(q)^{2}{\bigr ]}{\bigl [}1-R(q^{2})R(q){\bigr ]}}$

${\displaystyle \theta _{3}(q^{1/5})^{2}-\theta _{3}(q)^{2}={\bigl [}\theta _{3}(q)^{2}-\theta _{3}(q^{5})^{2}{\bigr ]}{\biggl [}1+{\frac {1}{R(q^{2})S(q)}}+R(q^{2})S(q)+{\frac {1}{R(q^{2})^{2}}}+R(q^{2})^{2}+{\frac {1}{S(q)}}-S(q){\biggr ]}}$

${\displaystyle \theta _{4}(q)^{2}-\theta _{4}(q^{1/5})^{2}={\bigl [}\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}{\bigr ]}{\biggl [}1-{\frac {1}{R(q^{2})R(q)}}-R(q^{2})R(q)+{\frac {1}{R(q^{2})^{2}}}+R(q^{2})^{2}-{\frac {1}{R(q)}}+R(q){\biggr ]}}$

Teoremas dependientes del módulo

En combinación con el módulo elíptico, se pueden mostrar las siguientes fórmulas:

Estas son las fórmulas para el cuadrado del nomo elíptico:

${\displaystyle \theta _{4}[q(k)]=\theta _{4}[q(k)^{2}]{\sqrt[{8}]{1-k^{2}}}}$

${\displaystyle \theta _{4}[q(k)^{2}]=\theta _{3}[q(k)]{\sqrt[{8}]{1-k^{2}}}}$

${\displaystyle \theta _{3}[q(k)^{2}]=\theta _{3}[q(k)]\cos[{\tfrac {1}{2}}\arcsin(k)]}$

Y esta es una fórmula eficiente para el cubo del nomo:

${\displaystyle \theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}^{3}{\biggr \rangle }=\theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}{\biggr \rangle }\,3^{-1/2}{\bigl (}{\sqrt {2{\sqrt {t^{4}-t^{2}+1}}-t^{2}+2}}+{\sqrt {t^{2}+1}}\,{\bigr )}^{1/2}}$

Para todos los valores reales es válida la fórmula ahora mencionada. ${\displaystyle t\in \mathbb {R} }$

Y para esta fórmula se darán dos ejemplos:

Primer ejemplo de cálculo con el valor insertado: ${\displaystyle t=1}$

Segundo ejemplo de cálculo con el valor insertado: ${\displaystyle t=\Phi ^{-2}}$

La constante representa exactamente el número de proporción áurea . ${\displaystyle \Phi }$ ${\displaystyle \Phi ={\tfrac {1}{2}}({\sqrt {5}}+1)}$

Algunas identidades de series

Sumas con función theta en el resultado

La suma infinita ^{[8] [9]} de los recíprocos de los números de Fibonacci con índices impares tiene esta identidad:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{2n-1}}}={\frac {\sqrt {5}}{2}}\,\sum _{n=1}^{\infty }{\frac {2(\Phi ^{-2})^{n-1/2}}{1+(\Phi ^{-2})^{2n-1}}}={\frac {\sqrt {5}}{4}}\sum _{a=-\infty }^{\infty }{\frac {2(\Phi ^{-2})^{a-1/2}}{1+(\Phi ^{-2})^{2a-1}}}=}$

${\displaystyle ={\frac {\sqrt {5}}{4}}\,\theta _{2}(\Phi ^{-2})^{2}={\frac {\sqrt {5}}{8}}{\bigl [}\theta _{3}(\Phi ^{-1})^{2}-\theta _{4}(\Phi ^{-1})^{2}{\bigr ]}}$

Al no utilizar la expresión de la función theta, se puede formular la siguiente identidad entre dos sumas:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{2n-1}}}={\frac {\sqrt {5}}{4}}\,{\biggl [}\sum _{n=1}^{\infty }2\,\Phi ^{-(2n-1)^{2}/2}{\biggr ]}^{2}}$

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{2n-1}}}=1.82451515740692456814215840626732817332\ldots }$

También en este caso vuelve a aparecer el número de proporción áurea . ${\displaystyle \Phi ={\tfrac {1}{2}}({\sqrt {5}}+1)}$

Suma infinita de los recíprocos de los cuadrados de los números de Fibonacci:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{n}^{2}}}={\frac {5}{24}}{\bigl [}2\,\theta _{2}(\Phi ^{-2})^{4}-\theta _{3}(\Phi ^{-2})^{4}+1{\bigr ]}={\frac {5}{24}}{\bigl [}\theta _{3}(\Phi ^{-2})^{4}-2\,\theta _{4}(\Phi ^{-2})^{4}+1{\bigr ]}}$

Suma infinita de los recíprocos de los números de Pell con índices impares:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{P_{2n-1}}}={\frac {1}{\sqrt {2}}}\,\theta _{2}{\bigl [}({\sqrt {2}}-1)^{2}{\bigr ]}^{2}={\frac {1}{2{\sqrt {2}}}}{\bigl [}\theta _{3}({\sqrt {2}}-1)^{2}-\theta _{4}({\sqrt {2}}-1)^{2}{\bigr ]}}$

Sumas con función theta en el sumando

István Mező demostró las identidades de las dos siguientes series: ^[10]

${\displaystyle {\begin{aligned}\theta _{4}^{2}(q)&=iq^{\frac {1}{4}}\sum _{k=-\infty }^{\infty }q^{2k^{2}-k}\theta _{1}\left({\frac {2k-1}{2i}}\ln q,q\right),\\[6pt]\theta _{4}^{2}(q)&=\sum _{k=-\infty }^{\infty }q^{2k^{2}}\theta _{4}\left({\frac {k\ln q}{i}},q\right).\end{aligned}}}$

Estas relaciones son válidas para todos los 0 < q < 1 . Especializando los valores de q , tenemos las siguientes sumas libres de parámetros

${\displaystyle {\sqrt {\frac {\pi {\sqrt {e^{\pi }}}}{2}}}\cdot {\frac {1}{\Gamma ^{2}\left({\frac {3}{4}}\right)}}=i\sum _{k=-\infty }^{\infty }e^{\pi \left(k-2k^{2}\right)}\theta _{1}\left({\frac {i\pi }{2}}(2k-1),e^{-\pi }\right)}$

${\displaystyle {\sqrt {\frac {\pi }{2}}}\cdot {\frac {1}{\Gamma ^{2}\left({\frac {3}{4}}\right)}}=\sum _{k=-\infty }^{\infty }{\frac {\theta _{4}\left(ik\pi ,e^{-\pi }\right)}{e^{2\pi k^{2}}}}}$

Ceros de las funciones theta de Jacobi

Todos los ceros de las funciones theta de Jacobi son ceros simples y vienen dados por lo siguiente:

${\displaystyle {\begin{aligned}\vartheta (z;\tau )=\vartheta _{00}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {1}{2}}+{\frac {\tau }{2}}\\[3pt]\vartheta _{11}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau \\[3pt]\vartheta _{10}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {1}{2}}\\[3pt]\vartheta _{01}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {\tau }{2}}\end{aligned}}}$

donde m , n son números enteros arbitrarios.

Relación con la función zeta de Riemann

la relacion

${\displaystyle \vartheta \left(0;-{\frac {1}{\tau }}\right)=\left(-i\tau \right)^{\frac {1}{2}}\vartheta (0;\tau )}$

Fue utilizado por Riemann para demostrar la ecuación funcional de la función zeta de Riemann , mediante la transformada de Mellin.

${\displaystyle \Gamma \left({\frac {s}{2}}\right)\pi ^{-{\frac {s}{2}}}\zeta (s)={\frac {1}{2}}\int _{0}^{\infty }{\bigl (}\vartheta (0;it)-1{\bigr )}t^{\frac {s}{2}}{\frac {\mathrm {d} t}{t}}}$

que se puede demostrar que es invariante sustituyendo s por 1 − s . La integral correspondiente para z ≠ 0 se da en el artículo sobre la función zeta de Hurwitz .

Relación con la función elíptica de Weierstrass

Jacobi utilizó la función theta para construir (en una forma adaptada para un cálculo sencillo) sus funciones elípticas como los cocientes de las cuatro funciones theta anteriores, y también podría haberla utilizado para construir las funciones elípticas de Weierstrass , ya que

${\displaystyle \wp (z;\tau )=-{\big (}\log \vartheta _{11}(z;\tau ){\big )}''+c}$

donde la segunda derivada es con respecto a z y la constante c se define de modo que la expansión de Laurent de ℘ ( z ) en z = 0 tiene un término constante cero.

Relación con elq-función gamma

La cuarta función theta – y por tanto también las demás – está íntimamente conectada con la función q -gamma de Jackson a través de la relación ^[11]

${\displaystyle \left(\Gamma _{q^{2}}(x)\Gamma _{q^{2}}(1-x)\right)^{-1}={\frac {q^{2x(1-x)}}{\left(q^{-2};q^{-2}\right)_{\infty }^{3}\left(q^{2}-1\right)}}\theta _{4}\left({\frac {1}{2i}}(1-2x)\log q,{\frac {1}{q}}\right).}$

Relaciones con la función Dedekind eta

Sea η ( τ ) la función eta de Dedekind , y el argumento de la función theta como el nombre q = e ^πiτ . Entonces,

${\displaystyle {\begin{aligned}\theta _{2}(q)=\vartheta _{10}(0;\tau )&={\frac {2\eta ^{2}(2\tau )}{\eta (\tau )}},\\[3pt]\theta _{3}(q)=\vartheta _{00}(0;\tau )&={\frac {\eta ^{5}(\tau )}{\eta ^{2}\left({\frac {1}{2}}\tau \right)\eta ^{2}(2\tau )}}={\frac {\eta ^{2}\left({\frac {1}{2}}(\tau +1)\right)}{\eta (\tau +1)}},\\[3pt]\theta _{4}(q)=\vartheta _{01}(0;\tau )&={\frac {\eta ^{2}\left({\frac {1}{2}}\tau \right)}{\eta (\tau )}},\end{aligned}}}$

y,

${\displaystyle \theta _{2}(q)\,\theta _{3}(q)\,\theta _{4}(q)=2\eta ^{3}(\tau ).}$

Véase también las funciones modulares de Weber .

Módulo elíptico

El módulo elíptico es

${\displaystyle k(\tau )={\frac {\vartheta _{10}(0;\tau )^{2}}{\vartheta _{00}(0;\tau )^{2}}}}$

y el módulo elíptico complementario es

${\displaystyle k'(\tau )={\frac {\vartheta _{01}(0;\tau )^{2}}{\vartheta _{00}(0;\tau )^{2}}}}$

Derivadas de funciones theta

Estas son dos definiciones idénticas de la integral elíptica completa de segundo tipo:

${\displaystyle E(k)=\int _{0}^{\pi /2}{\sqrt {1-k^{2}\sin(\varphi )^{2}}}\partial \varphi }$

${\displaystyle E(k)={\frac {\pi }{2}}\sum _{a=0}^{\infty }{\frac {[(2a)!]^{2}}{(1-2a)16^{a}(a!)^{4}}}k^{2a}}$

Las derivadas de las funciones Theta Nullwert tienen estas series de MacLaurin:

${\displaystyle \theta _{2}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{2}(x)={\frac {1}{2}}x^{-3/4}+\sum _{n=1}^{\infty }{\frac {1}{2}}(2n+1)^{2}x^{(2n-1)(2n+3)/4}}$

${\displaystyle \theta _{3}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{3}(x)=2+\sum _{n=1}^{\infty }2(n+1)^{2}x^{n(n+2)}}$

${\displaystyle \theta _{4}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{4}(x)=-2+\sum _{n=1}^{\infty }2(n+1)^{2}(-1)^{n+1}x^{n(n+2)}}$

Las derivadas de las funciones theta de valor cero ^[12] son ​​las siguientes:

${\displaystyle \theta _{2}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{2}(x)={\frac {1}{2\pi x}}\theta _{2}(x)\theta _{3}(x)^{2}E{\biggl [}{\frac {\theta _{2}(x)^{2}}{\theta _{3}(x)^{2}}}{\biggr ]}}$

${\displaystyle \theta _{3}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{3}(x)=\theta _{3}(x){\bigl [}\theta _{3}(x)^{2}+\theta _{4}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\theta _{3}(x)^{2}-\theta _{4}(x)^{2}}{\theta _{3}(x)^{2}+\theta _{4}(x)^{2}}}{\biggr ]}-{\frac {\theta _{4}(x)^{2}}{4\,x}}{\biggr \}}}$

${\displaystyle \theta _{4}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{4}(x)=\theta _{4}(x){\bigl [}\theta _{3}(x)^{2}+\theta _{4}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\theta _{3}(x)^{2}-\theta _{4}(x)^{2}}{\theta _{3}(x)^{2}+\theta _{4}(x)^{2}}}{\biggr ]}-{\frac {\theta _{3}(x)^{2}}{4\,x}}{\biggr \}}}$

Las dos últimas fórmulas mencionadas son válidas para todos los números reales del intervalo de definición real: ${\displaystyle -1<x<1\,\cap \,x\in \mathbb {R} }$

Y estas dos últimas funciones derivadas theta están relacionadas entre sí de esta manera:

${\displaystyle \vartheta _{4}(x){\biggl [}{\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{3}(x){\biggr ]}-\vartheta _{3}(x){\biggl [}{\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{4}(x){\biggr ]}={\frac {1}{4\,x}}\,\theta _{3}(x)\,\theta _{4}(x){\bigl [}\theta _{3}(x)^{4}-\theta _{4}(x)^{4}{\bigr ]}}$

Las derivadas de los cocientes de dos de las tres funciones theta mencionadas aquí siempre tienen una relación racional con esas tres funciones:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {\theta _{2}(x)}{\theta _{3}(x)}}={\frac {\theta _{2}(x)\,\theta _{4}(x)^{4}}{4\,x\,\theta _{3}(x)}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {\theta _{2}(x)}{\theta _{4}(x)}}={\frac {\theta _{2}(x)\,\theta _{3}(x)^{4}}{4\,x\,\theta _{4}(x)}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {\theta _{3}(x)}{\theta _{4}(x)}}={\frac {\theta _{3}(x)^{5}-\theta _{3}(x)\,\theta _{4}(x)^{4}}{4\,x\,\theta _{4}(x)}}}$

Para obtener estas fórmulas de derivación, consulte los artículos Nome (matemáticas) y Función lambda modular .

Integrales de funciones theta

Para las funciones theta estas integrales ^[13] son ​​válidas:

${\displaystyle \int _{0}^{1}\theta _{2}(x)\,\mathrm {d} x=\sum _{k=-\infty }^{\infty }{\frac {4}{(2k+1)^{2}+4}}=\pi \tanh(\pi )\approx 3.129881}$

${\displaystyle \int _{0}^{1}\theta _{3}(x)\,\mathrm {d} x=\sum _{k=-\infty }^{\infty }{\frac {1}{k^{2}+1}}=\pi \coth(\pi )\approx 3.153348}$

${\displaystyle \int _{0}^{1}\theta _{4}(x)\,\mathrm {d} x=\sum _{k=-\infty }^{\infty }{\frac {(-1)^{k}}{k^{2}+1}}=\pi \,\operatorname {csch} (\pi )\approx 0.272029}$

Los resultados finales que ahora se muestran se basan en las fórmulas generales de suma de Cauchy.

Una solución a la ecuación del calor.

La función theta de Jacobi es la solución fundamental de la ecuación del calor unidimensional con condiciones de contorno espacialmente periódicas. ^[14] Tomando z = x como real y τ = it con t real y positivo, podemos escribir

${\displaystyle \vartheta (x;it)=1+2\sum _{n=1}^{\infty }\exp \left(-\pi n^{2}t\right)\cos(2\pi nx)}$

que resuelve la ecuación del calor

${\displaystyle {\frac {\partial }{\partial t}}\vartheta (x;it)={\frac {1}{4\pi }}{\frac {\partial ^{2}}{\partial x^{2}}}\vartheta (x;it).}$

Esta solución de función theta es 1-periódica en x , y cuando t → 0 se aproxima a la función delta periódica , o peine de Dirac , en el sentido de distribuciones

${\displaystyle \lim _{t\to 0}\vartheta (x;it)=\sum _{n=-\infty }^{\infty }\delta (x-n)}$.

Las soluciones generales del problema del valor inicial espacialmente periódico para la ecuación del calor se pueden obtener convolucionando los datos iniciales en t = 0 con la función theta.

Relación con el grupo Heisenberg

La función theta de Jacobi es invariante bajo la acción de un subgrupo discreto del grupo de Heisenberg . Esta invariancia se presenta en el artículo sobre la representación theta del grupo de Heisenberg.

Generalizaciones

Si F es una forma cuadrática en n variables, entonces la función theta asociada con F es

${\displaystyle \theta _{F}(z)=\sum _{m\in \mathbb {Z} ^{n}}e^{2\pi izF(m)}}$

con la suma extendiéndose sobre la red de números enteros . Esta función theta es una forma modular de peso ⁠ ${\displaystyle \mathbb {Z} ^{n}}$norte/2⁠ (en un subgrupo adecuadamente definido) del grupo modular . En la expansión de Fourier,

${\displaystyle {\hat {\theta }}_{F}(z)=\sum _{k=0}^{\infty }R_{F}(k)e^{2\pi ikz},}$

los números R _F ( k ) se denominan números de representación de la forma.

Serie theta de un personaje de Dirichlet

Para χ un carácter primitivo de Dirichlet módulo q y ν = ⁠1 − χ (−1)/2⁠ entonces

${\displaystyle \theta _{\chi }(z)={\frac {1}{2}}\sum _{n=-\infty }^{\infty }\chi (n)n^{\nu }e^{2i\pi n^{2}z}}$

es un peso ⁠1/2⁠ + ν forma modular de nivel 4 q ² y personaje

${\displaystyle \chi (d)\left({\frac {-1}{d}}\right)^{\nu },}$

lo que significa ^[15]

${\displaystyle \theta _{\chi }\left({\frac {az+b}{cz+d}}\right)=\chi (d)\left({\frac {-1}{d}}\right)^{\nu }\left({\frac {\theta _{1}\left({\frac {az+b}{cz+d}}\right)}{\theta _{1}(z)}}\right)^{1+2\nu }\theta _{\chi }(z)}$

cuando sea

${\displaystyle a,b,c,d\in \mathbb {Z} ^{4},ad-bc=1,c\equiv 0{\bmod {4}}q^{2}.}$

Función theta de Ramanujan

Función theta de Riemann

Dejar

${\displaystyle \mathbb {H} _{n}=\left\{F\in M(n,\mathbb {C} )\,{\big |}\,F=F^{\mathsf {T}}\,,\,\operatorname {Im} F>0\right\}}$

ser el conjunto de matrices cuadradas simétricas cuya parte imaginaria es definida positiva . se llama semiespacio superior de Siegel y es el análogo multidimensional del semiplano superior . El análogo n -dimensional del grupo modular es el grupo simpléctico Sp(2 n , ) ; para norte = 1 , Sp(2, ) = SL(2, ) . El análogo n -dimensional de los subgrupos de congruencia lo desempeña ${\displaystyle \mathbb {H} _{n}}$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle \mathbb {Z} }$

${\displaystyle \ker {\big \{}\operatorname {Sp} (2n,\mathbb {Z} )\to \operatorname {Sp} (2n,\mathbb {Z} /k\mathbb {Z} ){\big \}}.}$

Entonces, dado τ ∈ ${\displaystyle \mathbb {H} _{n}}$ , la función theta de Riemann se define como

${\displaystyle \theta (z,\tau )=\sum _{m\in \mathbb {Z} ^{n}}\exp \left(2\pi i\left({\tfrac {1}{2}}m^{\mathsf {T}}\tau m+m^{\mathsf {T}}z\right)\right).}$

Aquí, z ∈ ${\displaystyle \mathbb {C} ^{n}}$ es un vector complejo de n dimensiones y el superíndice T denota la transpuesta . La función theta de Jacobi es entonces un caso especial, con n = 1 y τ ∈ ${\displaystyle \mathbb {H} }$ donde es el semiplano superior . Una aplicación importante de la función theta de Riemann es que permite dar fórmulas explícitas para funciones meromórficas en superficies compactas de Riemann , así como otros objetos auxiliares que ocupan un lugar destacado en su teoría de funciones, al tomar τ como la matriz de período con respecto a una base canónica para su primer grupo de homología . ${\displaystyle \mathbb {H} }$

La theta de Riemann converge absoluta y uniformemente en subconjuntos compactos de . ${\displaystyle \mathbb {C} ^{n}\times \mathbb {H} _{n}}$

La ecuación funcional es

${\displaystyle \theta (z+a+\tau b,\tau )=\exp \left(2\pi i\left(-b^{\mathsf {T}}z-{\tfrac {1}{2}}b^{\mathsf {T}}\tau b\right)\right)\theta (z,\tau )}$

que es válido para todos los vectores a , b ∈ ${\displaystyle \mathbb {Z} ^{n}}$ y para todos z ∈ ${\displaystyle \mathbb {C} ^{n}}$ y τ ∈ ${\displaystyle \mathbb {H} _{n}}$ .

serie poincaré

La serie de Poincaré generaliza la serie theta a formas automorfas con respecto a grupos fucsianos arbitrarios .

Derivación de los valores theta.

Identidad de la función beta de Euler

A continuación, se derivarán tres valores importantes de la función theta como ejemplos:

Así se define la función beta de Euler en su forma reducida:

${\displaystyle \beta (x)={\frac {\Gamma (x)^{2}}{\Gamma (2x)}}}$

En general, para todos los números naturales es válida esta fórmula de la función beta de Euler: ${\displaystyle n\in \mathbb {N} }$

${\displaystyle {\frac {4^{-1/(n+2)}}{n+2}}\csc {\bigl (}{\frac {\pi }{n+2}}{\bigr )}\beta {\biggl [}{\frac {n}{2(n+2)}}{\biggr ]}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{n+2}+1}}}\,\mathrm {d} x}$

Integrales elípticas ejemplares

A continuación se derivan algunos valores singulares integrales elípticos ^{[16] :}

Combinación de las identidades integrales con el nomo.

La función del nombre elíptico tiene estos valores importantes:

${\displaystyle q({\tfrac {1}{2}}{\sqrt {2}})=\exp(-\pi )}$

${\displaystyle q[{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})]=\exp(-{\sqrt {3}}\,\pi )}$

${\displaystyle q({\sqrt {2}}-1)=\exp(-{\sqrt {2}}\,\pi )}$

Para comprobar la exactitud de estos valores de nome, consulte el artículo Nome (matemáticas) !

Sobre la base de estas identidades integrales y la definición e identidades de las funciones theta mencionadas anteriormente en la misma sección de este artículo, ahora se determinarán valores theta cero ejemplares:

${\displaystyle \theta _{3}[\exp(-\pi )]=\theta _{3}[q({\tfrac {1}{2}}{\sqrt {2}})]={\sqrt {2\pi ^{-1}K({\tfrac {1}{2}}{\sqrt {2}})}}=2^{-1/2}\pi ^{-1/2}\beta ({\tfrac {1}{4}})^{1/2}=2^{-1/4}{\sqrt[{4}]{\pi }}\,{\Gamma {\bigl (}{\tfrac {3}{4}}{\bigr )}}^{-1}}$

${\displaystyle \theta _{3}[\exp(-{\sqrt {3}}\,\pi )]=\theta _{3}{\bigl \{}q{\bigl [}{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}{\bigr \}}={\sqrt {2\pi ^{-1}K{\bigl [}{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}}}=2^{-1/6}3^{-1/8}\pi ^{-1/2}\beta ({\tfrac {1}{3}})^{1/2}}$

${\displaystyle \theta _{3}[\exp(-{\sqrt {2}}\,\pi )]=\theta _{3}[q({\sqrt {2}}-1)]={\sqrt {2\pi ^{-1}K({\sqrt {2}}-1)}}=2^{-1/8}\cos({\tfrac {1}{8}}\pi )\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}$

${\displaystyle \theta _{4}[\exp(-{\sqrt {2}}\,\pi )]=\theta _{4}[q({\sqrt {2}}-1)]={\sqrt[{4}]{2{\sqrt {2}}-2}}\,{\sqrt {2\pi ^{-1}K({\sqrt {2}}-1)}}=2^{-1/4}\cos({\tfrac {1}{8}}\pi )^{1/2}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}$

Secuencias de partición y productos Pochhammer.

Secuencia de números de partición regular

La secuencia de partición regular en sí misma indica el número de formas en que un número entero positivo se puede dividir en sumandos enteros positivos. Para los números hasta , los números de partición asociados con todas las particiones numéricas asociadas se enumeran en la siguiente tabla: ${\displaystyle P(n)}$ ${\displaystyle n}$ ${\displaystyle n=1}$ ${\displaystyle n=5}$ ${\displaystyle P}$

La función generadora de la secuencia numérica de partición regular se puede representar mediante el producto Pochhammer de la siguiente manera:

${\displaystyle \sum _{k=0}^{\infty }P(k)x^{k}={\frac {1}{(x;x)_{\infty }}}=\theta _{3}(x)^{-1/6}\theta _{4}(x)^{-2/3}{\biggl [}{\frac {\theta _{3}(x)^{4}-\theta _{4}(x)^{4}}{16\,x}}{\biggr ]}^{-1/24}}$

La suma del producto de Pochhammer ahora mencionado se describe mediante el teorema del número pentagonal de esta manera:

${\displaystyle (x;x)_{\infty }=1+\sum _{n=1}^{\infty }{\bigl [}-x^{{\text{Fn}}(2n-1)}-x^{{\text{Kr}}(2n-1)}+x^{{\text{Fn}}(2n)}+x^{{\text{Kr}}(2n)}{\bigr ]}}$

Las siguientes definiciones básicas se aplican a los números pentagonales y a los números de los naipes:

${\displaystyle {\text{Fn}}(z)={\tfrac {1}{2}}z(3z-1)}$

${\displaystyle {\text{Kr}}(z)={\tfrac {1}{2}}z(3z+1)}$

Como aplicación adicional ^[17] se obtiene una fórmula para la tercera potencia del producto de Euler:

${\displaystyle (x;x)^{3}=\prod _{n=1}^{\infty }(1-x^{n})^{3}=\sum _{m=0}^{\infty }(-1)^{m}(2m+1)x^{m(m+1)/2}}$

Secuencia estricta de números de partición

Y la secuencia de partición estricta indica el número de formas en que dicho número entero positivo se puede dividir en sumandos enteros positivos de modo que cada sumando aparezca como máximo una vez ^[18] y ningún valor de sumando ocurra repetidamente. También se genera exactamente la misma secuencia ^[19] si en la partición solo se incluyen sumandos impares, pero estos sumandos impares pueden ocurrir más de una vez. Ambas representaciones de la secuencia numérica de partición estricta se comparan en la siguiente tabla: ${\displaystyle Q(n)}$ ${\displaystyle n}$

La función generadora de la secuencia numérica de partición estricta se puede representar utilizando el producto de Pochhammer:

${\displaystyle \sum _{k=0}^{\infty }Q(k)x^{k}={\frac {1}{(x;x^{2})_{\infty }}}=\theta _{3}(x)^{1/6}\theta _{4}(x)^{-1/3}{\biggl [}{\frac {\theta _{3}(x)^{4}-\theta _{4}(x)^{4}}{16\,x}}{\biggr ]}^{1/24}}$

Secuencia numérica de sobrepartición

La serie de Maclaurin para el recíproco de la función ϑ ₀₁ tiene los números de la secuencia de sobrepartición como coeficientes con signo positivo: ^[20]

${\displaystyle {\frac {1}{\theta _{4}(x)}}=\prod _{n=1}^{\infty }{\frac {1+x^{n}}{1-x^{n}}}=\sum _{k=0}^{\infty }{\overline {P}}(k)x^{k}}$

${\displaystyle {\frac {1}{\theta _{4}(x)}}=1+2x+4x^{2}+8x^{3}+14x^{4}+24x^{5}+40x^{6}+64x^{7}+100x^{8}+154x^{9}+232x^{10}+\dots }$

Si, para un número dado , todas las particiones están configuradas de tal manera que el tamaño del sumando nunca aumenta, y todos aquellos sumandos que no tienen un sumando del mismo tamaño a la izquierda de sí mismos se pueden marcar para cada partición de este tipo, entonces será el número resultante ^[21] de las particiones marcadas dependiendo de la función de sobrepartición . ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle {\overline {P}}(k)}$

Primer ejemplo:

${\displaystyle {\overline {P}}(4)=14}$

Estas 14 posibilidades de marcas de partición existen para la suma 4:

Segundo ejemplo:

${\displaystyle {\overline {P}}(5)=24}$

Estas 24 posibilidades de marcas de partición existen para la suma 5:

Relaciones de las secuencias de números de partición entre sí.

En la Enciclopedia en línea de secuencias enteras (OEIS), la secuencia de números de partición regulares está bajo el código A000041, la secuencia de particiones estrictas está bajo el código A000009 y la secuencia de superparticiones está bajo el código A015128. Todas las particiones principales del índice son pares. ${\displaystyle P(n)}$ ${\displaystyle Q(n)}$ ${\displaystyle {\overline {P}}(n)}$ ${\displaystyle n=1}$

La secuencia de superparticiones se puede escribir con la secuencia de partición regular P ^[22] y la secuencia de partición estricta Q ^[23] se puede generar así: ${\displaystyle {\overline {P}}(n)}$

${\displaystyle {\overline {P}}(n)=\sum _{k=0}^{n}P(n-k)Q(k)}$

En la siguiente tabla de secuencias de números, se debe utilizar esta fórmula como ejemplo:

En relación con esta propiedad, la siguiente combinación de dos series de sumas también se puede configurar mediante la función ϑ ₀₁ :

${\displaystyle \theta _{4}(x)={\biggl [}\sum _{k=0}^{\infty }P(k)x^{k}{\biggr ]}^{-1}{\biggl [}\sum _{k=0}^{\infty }Q(k)x^{k}{\biggr ]}^{-1}}$

Notas

1. Véase, por ejemplo, https://dlmf.nist.gov/20.1. Tenga en cuenta que esto, en general, no equivale a la interpretación habitual cuando está fuera de la franja . Aquí, denota la rama principal del logaritmo complejo . ${\displaystyle (e^{z})^{\alpha }=e^{\alpha \operatorname {Log} e^{z}}}$ ${\displaystyle z}$ ${\displaystyle -\pi <\operatorname {Im} z\leq \pi }$ ${\displaystyle \operatorname {Log} }$
2. para todos con . ${\displaystyle \theta _{1}(q)=0}$ ${\displaystyle q\in \mathbb {C} }$ ${\displaystyle |q|<1}$

Referencias

1. Tyurin, Andrey N. (30 de octubre de 2002). "Cuantización, teoría de campos clásica y cuántica y funciones Theta". arXiv : matemáticas/0210466v1 .
2. Chang, Der-Chen (2011). "Núcleos térmicos para operadores elípticos y subelípticos" . Birkhäuser. pag. 7.
3. Conferencias Tata sobre Theta I. Clásicos modernos de Birkhäuser. Boston, MA: Birkhäuser Boston. 2007. pág. 4. doi :10.1007/978-0-8176-4577-9. ISBN 978-0-8176-4572-4.
4. Yi, Jinhee (2004). "Identidades de funciones theta y fórmulas explícitas para funciones theta y sus aplicaciones". Revista de Análisis y Aplicaciones Matemáticas . 292 (2): 381–400. doi : 10.1016/j.jmaa.2003.12.009 .
5. Berndt, Bruce C; Rebák, Örs (9 de enero de 2022). "Valores explícitos de la función Theta de Ramanujan ϕ (q)". Diario Hardy-Ramanujan . 44 : 8923. arXiv : 2112.11882 . doi : 10.46298/hrj.2022.8923 . S2CID  245851672.
6. Yi, Jinhee (15 de abril de 2004). "Identidades de funciones theta y fórmulas explícitas para funciones theta y sus aplicaciones". Revista de Análisis y Aplicaciones Matemáticas . 292 (2): 381–400. doi : 10.1016/j.jmaa.2003.12.009 .
7. Andreas Dieckmann: Tabla de productos infinitos Sumas infinitas Serie infinita, Theta elíptica. Physikalisches Institut Universität Bonn, abril del 1 de octubre de 2021.
8. Landau (1899) zitiert nach Borwein, página 94, ejercicio 3.
9. "Funciones numéricas, combinatorias y enteras: documentación de mpmath 1.1.0" . Consultado el 18 de julio de 2021 .
10. funciones trigonométricas q de Gosper ", Actas de la Sociedad Matemática Estadounidense , 141 (7): 2401–2410, doi : 10.1090/s0002-9939-2013-11576 -5
11. Mező, István (2012). "Una fórmula q-Raabe y una integral de la cuarta función theta de Jacobi". Revista de teoría de números . 133 (2): 692–704. doi : 10.1016/j.jnt.2012.08.025 . hdl : 2437/166217 .
12. Weisstein, Eric W. "Función alfa elíptica". MundoMatemático .
13. "integración - Integrales curiosas para funciones Theta de Jacobi $\int_0^1 \vartheta_n(0,q)dq$". 2022-08-13.
14. Ohyama, Yousuke (1995). "Relaciones diferenciales de funciones theta". Revista de Matemáticas de Osaka . 32 (2): 431–450. ISSN  0030-6126.
15. Shimura, Sobre formas modulares de peso medio integral.
16. "Valor singular integral elíptico". msu.edu . Consultado el 7 de abril de 2023 .
17. Identidades de función theta de Ramanujan que involucran la serie de Lambert
18. "code golf: particiones estrictas de un número entero positivo" . Consultado el 9 de marzo de 2022 .
19. "A000009 - OEIS". 2022-03-09.
20. Mahlburg, Karl (2004). "La función de sobrepartición módulo pequeñas potencias de 2". Matemáticas Discretas . 286 (3): 263–267. doi :10.1016/j.disc.2004.03.014.
21. Kim, Byungchan (28 de abril de 2009). "Lector mejorado de Elsevier". Matemáticas Discretas . 309 (8): 2528–2532. doi : 10.1016/j.disc.2008.05.007 .
22. Eric W. Weisstein (11 de marzo de 2022). "Función de partición P".
23. Eric W. Weisstein (11 de marzo de 2022). "Función de partición Q".

• Abramowitz, Milton ; Stegun, Irene A. (1964). Manual de funciones matemáticas . Nueva York: Publicaciones de Dover . segundo. 16,27 y siguientes. ISBN 978-0-486-61272-0.
• Akhiezer, Naum Illyich (1990) [1970]. Elementos de la Teoría de Funciones Elípticas . Traducciones AMS de monografías matemáticas. vol. 79. Providencia, Rhode Island: AMS . ISBN 978-0-8218-4532-5.
• Farkas, Hershel M.; Kra, Irwin (1980). Superficies Riemann . Nueva York: Springer-Verlag . cap. 6.ISBN​ 978-0-387-90465-8.. (para el tratamiento de Riemann theta)
• Hardy, GH ; Wright, EM (1959). Introducción a la teoría de los números (4ª ed.). Oxford: Prensa de Clarendon .
• Mumford, David (1983). Conferencias Tata sobre Theta I. Boston: Birkhauser . ISBN 978-3-7643-3109-2.
• Pierpont, James (1959). Funciones de una variable compleja . Nueva York: Publicaciones de Dover .
• Rauch, Harry E .; Farkas, Hershel M. (1974). Funciones Theta con aplicaciones a superficies de Riemann . Baltimore: Williams y Wilkins . ISBN 978-0-683-07196-2.
• Reinhardt, William P.; Walker, Peter L. (2010), "Funciones Theta", en Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), Manual de funciones matemáticas del NIST , Cambridge University Press, ISBN 978-0-521-19225-5, señor  2723248.
• Whittaker, et al ; Watson, GN (1927). Un curso de análisis moderno (4ª ed.). Cambridge: Prensa de la Universidad de Cambridge . cap. 21. (historia de las funciones θ de Jacobi )

Lectura adicional

• Farkas, Hershel M. (2008). "Funciones theta en análisis complejo y teoría de números". En Alladi, Krishnaswami (ed.). Encuestas en teoría de números . Avances en Matemáticas. vol. 17. Springer-Verlag . págs. 57–87. ISBN 978-0-387-78509-7. Zbl  1206.11055.
• Schoeneberg, Bruno (1974). "IX. Serie Theta". Funciones modulares elípticas . Die Grundlehren der mathematischen Wissenschaften. vol. 203. Springer-Verlag . págs. 203–226. ISBN 978-3-540-06382-7.
• Ackerman, Michael (1 de febrero de 1979). "Sobre las funciones generadoras de determinadas series de Eisenstein". Annalen Matemáticas . 244 (1): 75–81. doi :10.1007/BF01420339. S2CID  120045753.

Harry Rauch con Hershel M. Farkas: Theta funciona con aplicaciones a Riemann Surfaces, Williams y Wilkins, Baltimore MD 1974, ISBN 0-683-07196-3 .  

• Charles Hermite: Sur la résolution de l'Équation du cinquiéme degré Comptes rendus, CR Acad. Ciencia. París, núm. 11 de marzo de 1858.

Enlaces externos

• Moiseev Igor. "Funciones elípticas para Matlab y Octave".

Este artículo incorpora material de representaciones integrales de las funciones theta de Jacobi en PlanetMath , que tiene la licencia Creative Commons Attribution/Share-Alike License .