Espacio métrico

Espacio matemático con noción de distancia

El avión (un conjunto de puntos) puede estar equipado con diferentes métricas. En la métrica del taxi, los caminos rojo, amarillo y azul tienen la misma longitud (12) y son todos los caminos más cortos. En la métrica euclidiana , el camino verde tiene una longitud y es el único camino más corto, mientras que los caminos rojo, amarillo y azul siguen teniendo una longitud de 12. ${\displaystyle 6{\sqrt {2}}\approx 8.49}$

En matemáticas , un espacio métrico es un conjunto unido a una noción de distancia entre sus elementos , habitualmente llamados puntos . La distancia se mide mediante una función llamada función métrica o de distancia . ^[1] Los espacios métricos son el marco más general para estudiar muchos de los conceptos del análisis matemático y la geometría .

El ejemplo más conocido de un espacio métrico es el espacio euclidiano tridimensional con su noción habitual de distancia. Otros ejemplos bien conocidos son una esfera equipada con la distancia angular y el plano hiperbólico . Una métrica puede corresponder a una noción metafórica , en lugar de física, de distancia: por ejemplo, el conjunto de cadenas Unicode de 100 caracteres puede estar equipado con la distancia de Hamming , que mide la cantidad de caracteres que deben cambiarse para pasar de una cadena a otra.

Los espacios métricos, por ser muy generales, son una herramienta utilizada en muchas ramas diferentes de las matemáticas. Muchos tipos de objetos matemáticos tienen una noción natural de distancia y, por lo tanto, admiten la estructura de un espacio métrico, incluidas las variedades de Riemann , los espacios vectoriales normados y los grafos . En álgebra abstracta , los números p -ádicos surgen como elementos de la completitud de una estructura métrica sobre los números racionales . Los espacios métricos también se estudian por derecho propio en la geometría métrica ^[2] y el análisis sobre espacios métricos . ^[3]

Muchas de las nociones básicas del análisis matemático , incluidas las de bolas , completitud , así como las de uniformidad , Lipschitz y continuidad de Hölder , se pueden definir en el contexto de los espacios métricos. Otras nociones, como continuidad , compacidad y conjuntos abiertos y cerrados , se pueden definir para espacios métricos, pero también en el contexto aún más general de los espacios topológicos .

Definición e ilustración

Motivación

Diagrama que ilustra la distancia del círculo máximo (en cian) y la distancia en línea recta (en rojo) entre dos puntos P y Q en una esfera.

Para ver la utilidad de las diferentes nociones de distancia, considere la superficie de la Tierra como un conjunto de puntos. Podemos medir la distancia entre dos de esos puntos por la longitud del camino más corto a lo largo de la superficie , " en línea recta "; esto es particularmente útil para el transporte marítimo y la aviación. También podemos medir la distancia en línea recta entre dos puntos a través del interior de la Tierra; esta noción es, por ejemplo, natural en sismología , ya que corresponde aproximadamente al tiempo que tardan las ondas sísmicas en viajar entre esos dos puntos.

La noción de distancia codificada por los axiomas del espacio métrico tiene relativamente pocos requisitos. Esta generalidad otorga a los espacios métricos mucha flexibilidad. Al mismo tiempo, la noción es lo suficientemente fuerte como para codificar muchos hechos intuitivos acerca de lo que significa la distancia. Esto significa que los resultados generales acerca de los espacios métricos pueden aplicarse en muchos contextos diferentes.

Al igual que muchos conceptos matemáticos fundamentales, la métrica en un espacio métrico se puede interpretar de muchas maneras diferentes. Es posible que una métrica en particular no se considere mejor como una medida de la distancia física, sino, en cambio, como el costo de cambiar de un estado a otro (como en el caso de las métricas de Wasserstein en espacios de medidas ) o el grado de diferencia entre dos objetos (por ejemplo, la distancia de Hamming entre dos cadenas de caracteres o la distancia de Gromov-Hausdorff entre los propios espacios métricos).

Definición

Formalmente, un espacio métrico es un par ordenado ( M , d ) donde M es un conjunto y d es una métrica en M , es decir, una función que satisface los siguientes axiomas para todos los puntos : ^{[4] [5]} $${\displaystyle d\,\colon M\times M\to \mathbb {R} }$$ ${\displaystyle x,y,z\in M}$

1. La distancia de un punto a sí mismo es cero: $${\displaystyle d(x,x)=0}$$
2. (Positividad) La distancia entre dos puntos distintos siempre es positiva: $${\displaystyle {\text{If }}x\neq y{\text{, then }}d(x,y)>0}$$
3. ( Simetría ) La distancia de x a y es siempre la misma que la distancia de y a x : $${\displaystyle d(x,y)=d(y,x)}$$
4. La desigualdad triangular se cumple: Esta es una propiedad natural de las nociones físicas y metafóricas de distancia: puedes llegar a z desde x tomando un desvío a través de y , pero esto no hará que tu viaje sea más corto que el camino directo. $${\displaystyle d(x,z)\leq d(x,y)+d(y,z)}$$

Si la métrica d es inequívoca, a menudo se hace referencia mediante abuso de notación al "espacio métrico M ".

Tomando todos los axiomas excepto el segundo, se puede demostrar que la distancia siempre es no negativa: Por lo tanto, el segundo axioma puede debilitarse a y combinarse con el primero para hacer . ^[6] $${\displaystyle 0=d(x,x)\leq d(x,y)+d(y,x)=2d(x,y)}$$ ${\textstyle {\text{If }}x\neq y{\text{, then }}d(x,y)\neq 0}$ ${\textstyle d(x,y)=0\iff x=y}$

Ejemplos sencillos

Los números reales

Los números reales con la función de distancia dada por la diferencia absoluta forman un espacio métrico. Muchas propiedades de los espacios métricos y las funciones entre ellos son generalizaciones de conceptos del análisis real y coinciden con esos conceptos cuando se aplican a la recta real. ${\displaystyle d(x,y)=|y-x|}$

Métricas en espacios euclidianos

Comparación de las distancias de Chebyshev, Euclidiana y de taxi para la hipotenusa de un triángulo 3-4-5 en un tablero de ajedrez

El plano euclidiano puede estar equipado con muchas métricas diferentes. La distancia euclidiana familiar de las matemáticas escolares se puede definir mediante ${\displaystyle \mathbb {R} ^{2}}$ $${\displaystyle d_{2}((x_{1},y_{1}),(x_{2},y_{2}))={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}.}$$

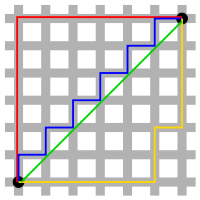
La distancia de taxi o de Manhattan se define y puede considerarse como la distancia que debe recorrer a lo largo de líneas horizontales y verticales para llegar de un punto a otro, como se ilustra en la parte superior del artículo. $${\displaystyle d_{1}((x_{1},y_{1}),(x_{2},y_{2}))=|x_{2}-x_{1}|+|y_{2}-y_{1}|}$$

La distancia máxima , , o distancia de Chebyshev se define por Esta distancia no tiene una explicación fácil en términos de trayectorias en el plano, pero aún así satisface los axiomas del espacio métrico. Se puede pensar en ella de manera similar al número de movimientos que tendría que hacer un rey en un tablero de ajedrez para viajar de un punto a otro en el espacio dado. ${\displaystyle L^{\infty }}$ $${\displaystyle d_{\infty }((x_{1},y_{1}),(x_{2},y_{2}))=\max\{|x_{2}-x_{1}|,|y_{2}-y_{1}|\}.}$$

De hecho, estas tres distancias, si bien tienen propiedades distintas, son similares en algunos aspectos. De manera informal, los puntos que están cerca en una de ellas también lo están en las otras. Esta observación se puede cuantificar con la fórmula que se cumple para cada par de puntos . $${\displaystyle d_{\infty }(p,q)\leq d_{2}(p,q)\leq d_{1}(p,q)\leq 2d_{\infty }(p,q),}$$ ${\displaystyle p,q\in \mathbb {R} ^{2}}$

Se puede definir una distancia radicalmente diferente estableciendo Utilizando corchetes de Iverson , En esta métrica discreta , todos los puntos distintos están separados por 1 unidad: ninguno de ellos está cerca uno del otro, y ninguno de ellos está muy lejos uno del otro tampoco. Intuitivamente, la métrica discreta ya no recuerda que el conjunto es un plano, sino que lo trata simplemente como un conjunto indiferenciado de puntos. $${\displaystyle d(p,q)={\begin{cases}0,&{\text{if }}p=q,\\1,&{\text{otherwise.}}\end{cases}}}$$ $${\displaystyle d(p,q)=[p\neq q]}$$

Todas estas métricas tienen sentido tanto en . ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{2}}$

Subespacios

Dado un espacio métrico ( M , d ) y un subconjunto , podemos considerar que A es un espacio métrico midiendo distancias de la misma manera que lo haríamos en M . Formalmente, la métrica inducida en A es una función definida por Por ejemplo, si tomamos la esfera bidimensional S ² como un subconjunto de , la métrica euclidiana en induce la métrica de línea recta en S ² descrita anteriormente. Dos ejemplos más útiles son el intervalo abierto (0, 1) y el intervalo cerrado [0, 1] considerados como subespacios de la línea real. ${\displaystyle A\subseteq M}$ ${\displaystyle d_{A}:A\times A\to \mathbb {R} }$ $${\displaystyle d_{A}(x,y)=d(x,y).}$$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbb {R} ^{3}}$

Historia

Arthur Cayley , en su artículo "Sobre la distancia", extendió los conceptos métricos más allá de la geometría euclidiana hacia dominios delimitados por una cónica en un espacio proyectivo. Su distancia se dio mediante el logaritmo de una razón cruzada . Cualquier proyectividad que deje estable la cónica también deja constante la razón cruzada, por lo que las isometrías son implícitas. Este método proporciona modelos para la geometría elíptica y la geometría hiperbólica , y Felix Klein , en varias publicaciones, estableció el campo de la geometría no euclidiana mediante el uso de la métrica de Cayley-Klein .

La idea de un espacio abstracto con propiedades métricas fue abordada en 1906 por René Maurice Fréchet ^[7] y el término espacio métrico fue acuñado por Felix Hausdorff en 1914. ^{[8] [9] [10]}

El trabajo de Fréchet sentó las bases para comprender la convergencia , la continuidad y otros conceptos clave en espacios no geométricos. Esto permitió a los matemáticos estudiar funciones y secuencias de una manera más amplia y flexible. Esto fue importante para el creciente campo del análisis funcional. Matemáticos como Hausdorff y Stefan Banach refinaron y expandieron aún más el marco de los espacios métricos. Hausdorff introdujo los espacios topológicos como una generalización de los espacios métricos. El trabajo de Banach en el análisis funcional se basó en gran medida en la estructura métrica. Con el tiempo, los espacios métricos se convirtieron en una parte central de las matemáticas modernas . Han influido en varios campos, incluidos la topología , la geometría y las matemáticas aplicadas . Los espacios métricos continúan desempeñando un papel crucial en el estudio de conceptos matemáticos abstractos.

Nociones básicas

Una función de distancia es suficiente para definir las nociones de cercanía y convergencia que se desarrollaron por primera vez en el análisis real . Las propiedades que dependen de la estructura de un espacio métrico se denominan propiedades métricas . Todo espacio métrico es también un espacio topológico , y algunas propiedades métricas también pueden reformularse sin referencia a la distancia en el lenguaje de la topología; es decir, son realmente propiedades topológicas .

La topología de un espacio métrico

Para cualquier punto x en un espacio métrico M y cualquier número real r > 0 , la esfera abierta de radio r alrededor de x se define como el conjunto de puntos que son estrictamente menores que la distancia r desde x : Esta es una forma natural de definir un conjunto de puntos que están relativamente cerca de x . Por lo tanto, un conjunto es un entorno de x (informalmente, contiene todos los puntos "suficientemente cercanos" a x ) si contiene una esfera abierta de radio r alrededor de x para algún r > 0 . $${\displaystyle B_{r}(x)=\{y\in M:d(x,y)<r\}.}$$ ${\displaystyle N\subseteq M}$

Un conjunto abierto es un conjunto que es un entorno de todos sus puntos. De ello se deduce que las bolas abiertas forman una base para una topología en M . En otras palabras, los conjuntos abiertos de M son exactamente las uniones de bolas abiertas. Como en cualquier topología, los conjuntos cerrados son los complementos de los conjuntos abiertos. Los conjuntos pueden ser tanto abiertos como cerrados, así como ni abiertos ni cerrados.

Esta topología no contiene toda la información sobre el espacio métrico. Por ejemplo, las distancias d ₁ , d ₂ y d _∞ definidas anteriormente inducen todas la misma topología en , aunque se comportan de manera diferente en muchos aspectos. De manera similar, con la métrica euclidiana y su subespacio, el intervalo (0, 1) con la métrica inducida son homeomorfos pero tienen propiedades métricas muy diferentes. ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} }$

Por el contrario, no a todo espacio topológico se le puede dar una métrica. Los espacios topológicos que son compatibles con una métrica se denominan metrizables y se comportan particularmente bien en muchos sentidos: en particular, son espacios paracompactos ^[11] de Hausdorff (por lo tanto, normales ) y primeros contables . ^[a] El teorema de metrización de Nagata-Smirnov proporciona una caracterización de la metrizabilidad en términos de otras propiedades topológicas, sin referencia a las métricas.

Convergencia

La convergencia de secuencias en el espacio euclidiano se define de la siguiente manera:

Una secuencia ( x _n ) converge a un punto x si para cada ε > 0 existe un entero N tal que para todo n > N , d ( x _n , x ) < ε .

La convergencia de secuencias en un espacio topológico se define de la siguiente manera:

Una secuencia ( x _n ) converge a un punto x si para cada conjunto abierto U que contiene x hay un entero N tal que para todo n > N , . ${\displaystyle x_{n}\in U}$

En los espacios métricos, ambas definiciones tienen sentido y son equivalentes. Este es un patrón general para las propiedades topológicas de los espacios métricos: si bien se pueden definir de una manera puramente topológica, a menudo hay una manera que utiliza la métrica que es más fácil de enunciar o que resulta más familiar a partir del análisis real.

Lo completo

De manera informal, un espacio métrico está completo si no tiene "puntos faltantes": toda secuencia que parece que debería converger a algo en realidad converge.

Para ser más precisos: una sucesión ( x _n ) en un espacio métrico M es de Cauchy si para cada ε > 0 existe un entero N tal que para todo m , n > N , d ( x _m , x _n ) < ε . Por la desigualdad triangular, cualquier sucesión convergente es de Cauchy: si x _m y x _n están a menos de ε del límite, entonces están a menos de 2ε entre sí. Si lo inverso es cierto (toda sucesión de Cauchy en M converge), entonces M es completa.

Los espacios euclidianos son completos, al igual que las otras métricas descritas anteriormente. Dos ejemplos de espacios que no son completos son (0, 1) y los racionales, cada uno con la métrica inducida a partir de . Se puede pensar que (0, 1) "carece" de sus puntos finales 0 y 1. A los racionales les faltan todos los irracionales, ya que cualquier irracional tiene una secuencia de racionales que convergen hacia él en (por ejemplo, sus aproximaciones decimales sucesivas). Estos ejemplos muestran que la completitud no es una propiedad topológica, ya que es completo, pero el espacio homeomorfo (0, 1) no lo es. ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$

Esta noción de "puntos faltantes" se puede precisar. De hecho, cada espacio métrico tiene una completitud única , que es un espacio completo que contiene el espacio dado como un subconjunto denso . Por ejemplo, [0, 1] es la completitud de (0, 1) y los números reales son la completitud de los racionales.

Dado que los espacios completos son generalmente más fáciles de trabajar, las compleciones son importantes en toda la matemática. Por ejemplo, en álgebra abstracta, los números p -ádicos se definen como la compleción de los racionales bajo una métrica diferente. La compleción es particularmente común como herramienta en el análisis funcional . A menudo, uno tiene un conjunto de funciones agradables y una forma de medir las distancias entre ellas. Tomar la compleción de este espacio métrico da un nuevo conjunto de funciones que pueden ser menos agradables, pero sin embargo útiles porque se comportan de manera similar a las funciones agradables originales en formas importantes. Por ejemplo, las soluciones débiles a las ecuaciones diferenciales generalmente viven en una compleción (un espacio de Sobolev ) en lugar del espacio original de funciones agradables para el cual la ecuación diferencial realmente tiene sentido.

Espacios acotados y totalmente acotados

Diámetro de un conjunto.

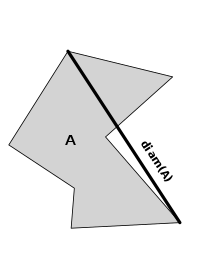
Un espacio métrico M está acotado si existe un r tal que ningún par de puntos en M está separado por una distancia mayor que r . ^[b] El menor de tales r se denominadiámetro deM.​

El espacio M se llama precompacto o totalmente acotado si para cada r > 0 hay una cobertura finita de M por bolas abiertas de radio r . Todo espacio totalmente acotado es acotado. Para ver esto, comience con una cobertura finita por r -bolas para algún r arbitrario . Como el subconjunto de M que consiste en los centros de estas bolas es finito, tiene un diámetro finito, digamos D . Por la desigualdad triangular, el diámetro de todo el espacio es como máximo D + 2 r . La recíproca no se cumple: un ejemplo de un espacio métrico que está acotado pero no totalmente acotado es (o cualquier otro conjunto infinito) con la métrica discreta. ${\displaystyle \mathbb {R} ^{2}}$

Compacidad

La compacidad es una propiedad topológica que generaliza las propiedades de un subconjunto cerrado y acotado del espacio euclidiano. Existen varias definiciones equivalentes de compacidad en espacios métricos:

1. Un espacio métrico M es compacto si cada cubierta abierta tiene una subcubierta finita (la definición topológica habitual).
2. Un espacio métrico M es compacto si cada secuencia tiene una subsecuencia convergente. (Para espacios topológicos generales esto se llama compacidad secuencial y no es equivalente a compacidad).
3. Un espacio métrico M es compacto si es completo y totalmente acotado. (Esta definición está escrita en términos de propiedades métricas y no tiene sentido para un espacio topológico general, pero es topológicamente invariante ya que es equivalente a compacidad.)

Un ejemplo de un espacio compacto es el intervalo cerrado [0, 1] .

La compacidad es importante por razones similares a la completitud: facilita la búsqueda de límites. Otra herramienta importante es el lema de números de Lebesgue , que muestra que para cualquier cobertura abierta de un espacio compacto, cada punto está relativamente profundo dentro de uno de los conjuntos de la cobertura.

Funciones entre espacios métricos

Diagrama de Euler de tipos de funciones entre espacios métricos.

A diferencia de lo que ocurre en el caso de los espacios topológicos o las estructuras algebraicas, como los grupos o los anillos , no existe un único tipo "correcto" de función que preserve la estructura entre espacios métricos. En cambio, se trabaja con distintos tipos de funciones en función de los objetivos que se persigan. A lo largo de esta sección, supongamos que y son dos espacios métricos. Las palabras "función" y "mapa" se utilizan indistintamente. ${\displaystyle (M_{1},d_{1})}$ ${\displaystyle (M_{2},d_{2})}$

Isometrías

Una interpretación de un mapa "que preserva la estructura" es aquella que preserva completamente la función de distancia:

Una función preserva la distancia ^[12] si para cada par de puntos x e y en M ₁ , ${\displaystyle f:M_{1}\to M_{2}}$ $${\displaystyle d_{2}(f(x),f(y))=d_{1}(x,y).}$$

De los axiomas del espacio métrico se desprende que una función que preserva la distancia es inyectiva. Una función que preserva la distancia biyectiva se denomina isometría . ^[13] Un ejemplo quizás no obvio de una isometría entre espacios descrita en este artículo es la función definida por ${\displaystyle f:(\mathbb {R} ^{2},d_{1})\to (\mathbb {R} ^{2},d_{\infty })}$ $${\displaystyle f(x,y)=(x+y,x-y).}$$

Si existe una isometría entre los espacios M ₁ y M ₂ , se dice que son isométricos . Los espacios métricos que son isométricos son esencialmente idénticos .

Mapas continuos

En el otro extremo del espectro, se puede olvidar por completo la estructura métrica y estudiar las aplicaciones continuas , que solo conservan la estructura topológica. Existen varias definiciones equivalentes de continuidad para espacios métricos. Las más importantes son:

• Definición topológica. Una función es continua si para cada conjunto abierto U en M ₂ , la preimagen es abierta. ${\displaystyle f\,\colon M_{1}\to M_{2}}$ ${\displaystyle f^{-1}(U)}$
• Continuidad secuencial . Una funciónes continua si siempre que una secuencia ( x _n ) converge a un punto x en M ₁ , la secuenciaconverge al punto f ( x ) en M ₂ . ${\displaystyle f\,\colon M_{1}\to M_{2}}$ ${\displaystyle f(x_{1}),f(x_{2}),\ldots }$

(Estas dos primeras definiciones no son equivalentes para todos los espacios topológicos).

• Definición de ε–δ. Una función es continua si para cada punto x en M ₁ y cada ε > 0 existe δ > 0 tal que para todo y en M ₁ tenemos ${\displaystyle f\,\colon M_{1}\to M_{2}}$ $${\displaystyle d_{1}(x,y)<\delta \implies d_{2}(f(x),f(y))<\varepsilon .}$$

Un homeomorfismo es una biyección continua cuya inversa también es continua; si existe un homeomorfismo entre M ₁ y M ₂ , se dice que son homeomorfos . Los espacios homeomorfos son iguales desde el punto de vista de la topología, pero pueden tener propiedades métricas muy diferentes. Por ejemplo, es ilimitado y completo, mientras que (0, 1) es acotado pero no completo. ${\displaystyle \mathbb {R} }$

Mapas uniformemente continuos

Una función es uniformemente continua si para cada número real ε > 0 existe δ > 0 tal que para todos los puntos x e y en M ₁ tales que , tenemos ${\displaystyle f\,\colon M_{1}\to M_{2}}$ ${\displaystyle d(x,y)<\delta }$ $${\displaystyle d_{2}(f(x),f(y))<\varepsilon .}$$

La única diferencia entre esta definición y la definición de continuidad ε–δ es el orden de los cuantificadores: la elección de δ debe depender solo de ε y no del punto x . Sin embargo, este cambio sutil hace una gran diferencia. Por ejemplo, las funciones uniformemente continuas toman secuencias de Cauchy en M ₁ en secuencias de Cauchy en M ₂ . En otras palabras, la continuidad uniforme conserva algunas propiedades métricas que no son puramente topológicas.

Por otra parte, el teorema de Heine-Cantor establece que si M ₁ es compacto, entonces toda función continua es uniformemente continua. En otras palabras, la continuidad uniforme no puede distinguir ninguna característica no topológica de los espacios métricos compactos.

Mapas y contracciones de Lipschitz

Una función de Lipschitz es una función que estira las distancias como máximo por un factor acotado. Formalmente, dado un número real K > 0 , la función es K - Lipschitz si Las funciones de Lipschitz son particularmente importantes en la geometría métrica, ya que proporcionan más flexibilidad que las funciones que preservan la distancia, pero aún hacen un uso esencial de la métrica. ^[14] Por ejemplo, una curva en un espacio métrico es rectificable (tiene una longitud finita) si y solo si tiene una reparametrización de Lipschitz. ${\displaystyle f\,\colon M_{1}\to M_{2}}$ $${\displaystyle d_{2}(f(x),f(y))\leq Kd_{1}(x,y)\quad {\text{for all}}\quad x,y\in M_{1}.}$$

A una función de 1-Lipschitz a veces se la denomina función no expansiva o función métrica . Las funciones métricas se consideran comúnmente morfismos de la categoría de espacios métricos .

Una función de K -Lipschitz para K < 1 se denomina contracción . El teorema del punto fijo de Banach establece que si M es un espacio métrico completo, entonces toda contracción admite un único punto fijo . Si el espacio métrico M es compacto, el resultado se cumple para una condición ligeramente más débil en f : una función admite un único punto fijo si ${\displaystyle f:M\to M}$ ${\displaystyle f:M\to M}$ $${\displaystyle d(f(x),f(y))<d(x,y)\quad {\mbox{for all}}\quad x\neq y\in M_{1}.}$$

Cuasi-isometrías

Una cuasi-isometría es una función que preserva la "estructura a gran escala" de un espacio métrico. Las cuasi-isometrías no necesitan ser continuas. Por ejemplo, y su subespacio son cuasi-isométricos, aunque uno sea conexo y el otro discreto. La relación de equivalencia de la cuasi-isometría es importante en la teoría geométrica de grupos : el lema de Švarc-Milnor establece que todos los espacios en los que un grupo actúa geométricamente son cuasi-isométricos. ^[15] ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {Z} ^{2}}$

Formalmente, el mapa es una incrustación cuasi-isométrica si existen constantes A ≥ 1 y B ≥ 0 tales que Es una cuasi-isometría si además es cuasi-sobreyectiva , es decir, hay una constante C ≥ 0 tal que cada punto en está a una distancia como máximo C de algún punto en la imagen . ${\displaystyle f\,\colon M_{1}\to M_{2}}$ $${\displaystyle {\frac {1}{A}}d_{2}(f(x),f(y))-B\leq d_{1}(x,y)\leq Ad_{2}(f(x),f(y))+B\quad {\text{ for all }}\quad x,y\in M_{1}.}$$ ${\displaystyle M_{2}}$ ${\displaystyle f(M_{1})}$

Nociones de equivalencia del espacio métrico

Dados dos espacios métricos y : ${\displaystyle (M_{1},d_{1})}$ ${\displaystyle (M_{2},d_{2})}$

• Se denominan homeomorfos (topológicamente isomorfos) si existe un homeomorfismo entre ellos (es decir, una biyección continua con una inversa continua). Si y la función identidad es un homeomorfismo, entonces se dice que y son topológicamente equivalentes . ${\displaystyle M_{1}=M_{2}}$ ${\displaystyle d_{1}}$ ${\displaystyle d_{2}}$
• Se denominan uniformistas (uniformemente isomorfos) si existe un isomorfismo uniforme entre ellos (es decir, una biyección uniformemente continua con una inversa uniformemente continua).
• Se denominan homeomorfos bilipschitz si existe una biyección bilipschitz entre ellos (es decir, una biyección de Lipschitz con una inversa de Lipschitz).
• Se denominan isométricos si existe entre ellos una isometría (biyectiva) . En este caso, los dos espacios métricos son esencialmente idénticos.
• Se llaman cuasi-isométricos si existe una cuasi-isometría entre ellos.

Espacios métricos con estructura adicional

Espacios vectoriales normados

Un espacio vectorial normado es un espacio vectorial equipado con una norma , que es una función que mide la longitud de los vectores. La norma de un vector v se denota típicamente por . Cualquier espacio vectorial normado puede estar equipado con una métrica en la que la distancia entre dos vectores x e y está dada por Se dice que la métrica d está inducida por la norma . Por el contrario, ^[16] si una métrica d en un espacio vectorial X es ${\displaystyle \lVert v\rVert }$ $${\displaystyle d(x,y):=\lVert x-y\rVert .}$$ ${\displaystyle \lVert {\cdot }\rVert }$

• invariante de traducción: para cada x , y y a en X ; y ${\displaystyle d(x,y)=d(x+a,y+a)}$
• absolutamente homogénea :para cadaxeyenXy número realα; ${\displaystyle d(\alpha x,\alpha y)=|\alpha |d(x,y)}$

entonces es la métrica inducida por la norma . Una relación similar se da entre las seminormas y las pseudometrías . $${\displaystyle \lVert x\rVert :=d(x,0).}$$

Entre los ejemplos de métricas inducidas por una norma se encuentran las métricas d ₁ , d ₂ y d _∞ en , que son inducidas por la norma de Manhattan , la norma euclidiana y la norma máxima , respectivamente. De manera más general, la incrustación de Kuratowski permite ver cualquier espacio métrico como un subespacio de un espacio vectorial normado. ${\displaystyle \mathbb {R} ^{2}}$

Los espacios vectoriales normados de dimensión infinita, en particular los espacios de funciones, se estudian en el análisis funcional . La completitud es particularmente importante en este contexto: un espacio vectorial normado completo se conoce como espacio de Banach . Una propiedad inusual de los espacios vectoriales normados es que las transformaciones lineales entre ellos son continuas si y solo si son Lipschitz. Tales transformaciones se conocen como operadores acotados .

Espacios de longitud

Una posible aproximación para la longitud de arco de una curva. La aproximación nunca es mayor que la longitud de arco, lo que justifica la definición de longitud de arco como suprema .

Una curva en un espacio métrico ( M , d ) es una función continua . La longitud de γ se mide por En general, este supremo puede ser infinito; una curva de longitud finita se llama rectificable . ^[17] Supongamos que la longitud de la curva γ es igual a la distancia entre sus puntos finales, es decir, es el camino más corto posible entre sus puntos finales. Después de la reparametrización por longitud de arco, γ se convierte en una geodésica : una curva que es una función que preserva la distancia. ^[15] Una geodésica es el camino más corto posible entre dos de sus puntos. ^[c] ${\displaystyle \gamma :[0,T]\to M}$ $${\displaystyle L(\gamma )=\sup _{0=x_{0}<x_{1}<\cdots <x_{n}=T}\left\{\sum _{k=1}^{n}d(\gamma (x_{k-1}),\gamma (x_{k}))\right\}.}$$

Un espacio métrico geodésico es un espacio métrico que admite una geodésica entre dos puntos cualesquiera. Los espacios y son ambos espacios métricos geodésicos. En , las geodésicas son únicas, pero en , a menudo hay infinitas geodésicas entre dos puntos, como se muestra en la figura en la parte superior del artículo. ${\displaystyle (\mathbb {R} ^{2},d_{1})}$ ${\displaystyle (\mathbb {R} ^{2},d_{2})}$ ${\displaystyle (\mathbb {R} ^{2},d_{2})}$ ${\displaystyle (\mathbb {R} ^{2},d_{1})}$

El espacio M es un espacio de longitud (o la métrica d es intrínseca ) si la distancia entre dos puntos cualesquiera x e y es el ínfimo de las longitudes de los caminos entre ellos. A diferencia de un espacio métrico geodésico, no es necesario alcanzar el ínfimo. Un ejemplo de un espacio de longitud que no es geodésico es el plano euclidiano menos el origen: los puntos (1, 0) y (-1, 0) se pueden unir mediante caminos de longitud arbitrariamente cercana a 2, pero no mediante un camino de longitud 2. Un ejemplo de un espacio métrico que no es un espacio de longitud lo da la métrica de línea recta sobre la esfera: la línea recta entre dos puntos que pasan por el centro de la Tierra es más corta que cualquier camino a lo largo de la superficie.

Dado cualquier espacio métrico ( M , d ) , se puede definir una nueva función de distancia intrínseca d _intrínseca en M estableciendo la distancia entre los puntos x e y como el ínfimo de las d longitudes de los caminos entre ellos. Por ejemplo, si d es la distancia en línea recta en la esfera, entonces d _intrínseca es la distancia del círculo máximo. Sin embargo, en algunos casos d _intrínseca puede tener valores infinitos. Por ejemplo, si M es el copo de nieve de Koch con la métrica del subespacio d inducida a partir de , entonces la distancia intrínseca resultante es infinita para cualquier par de puntos distintos. ${\displaystyle \mathbb {R} ^{2}}$

Variedades de Riemann

Una variedad de Riemann es un espacio equipado con un tensor métrico de Riemann , que determina longitudes de vectores tangentes en cada punto. Esto puede considerarse como la definición de una noción de distancia infinitesimalmente. En particular, un camino diferenciable en una variedad de Riemann M tiene una longitud definida como la integral de la longitud del vector tangente al camino: En una variedad de Riemann conexa, uno define entonces la distancia entre dos puntos como el ínfimo de longitudes de caminos suaves entre ellos. Esta construcción se generaliza a otros tipos de métricas infinitesimales en variedades, como las métricas subriemannianas y de Finsler . ${\displaystyle \gamma :[0,T]\to M}$ $${\displaystyle L(\gamma )=\int _{0}^{T}|{\dot {\gamma }}(t)|dt.}$$

La métrica de Riemann está determinada únicamente por la función de distancia; esto significa que, en principio, toda la información sobre una variedad de Riemann se puede recuperar a partir de su función de distancia. Una dirección en la geometría métrica es encontrar formulaciones puramente métricas ( "sintéticas" ) de propiedades de variedades de Riemann. Por ejemplo, una variedad de Riemann es un espacio CAT( k ) (una condición sintética que depende puramente de la métrica) si y solo si su curvatura seccional está acotada superiormente por k . ^[20] Por lo tanto, los espacios CAT( k ) generalizan los límites de curvatura superior a los espacios métricos generales.

Espacios de medida métrica

El análisis real hace uso tanto de la métrica en como de la medida de Lebesgue . Por lo tanto, las generalizaciones de muchas ideas del análisis residen naturalmente en espacios de medida métrica: espacios que tienen tanto una medida como una métrica que son compatibles entre sí. Formalmente, un espacio de medida métrica es un espacio métrico equipado con una medida regular de Borel tal que cada bola tiene medida positiva. ^[21] Por ejemplo, los espacios euclidianos de dimensión n y, más generalmente, las variedades riemannianas n -dimensionales, tienen naturalmente la estructura de un espacio de medida métrica, equipado con la medida de Lebesgue . Ciertos espacios métricos fractales como la junta de Sierpiński pueden estar equipados con la medida de Hausdorff α-dimensional donde α es la dimensión de Hausdorff . En general, sin embargo, un espacio métrico puede no tener una elección "obvia" de medida. ${\displaystyle \mathbb {R} ^{n}}$

Una aplicación de los espacios de medida métrica es la generalización de la noción de curvatura de Ricci más allá de las variedades de Riemann. Así como los espacios CAT( k ) y Alexandrov generalizan los límites de curvatura seccional, los espacios RCD son una clase de espacios de medida métrica que generalizan los límites inferiores de la curvatura de Ricci. ^[22]

Otros ejemplos y aplicaciones

Gráficas y espacios métricos finitos

AEl espacio métrico es discreto si su topología inducida es la topología discreta . Aunque muchos conceptos, como completitud y compacidad, no son interesantes para tales espacios, son sin embargo un objeto de estudio en varias ramas de las matemáticas. En particular,Los espacios métricos finitos (aquellos que tienen un número finito de puntos) se estudian en combinatoria y en informática teórica . ^[23] Las incrustaciones en otros espacios métricos se estudian particularmente bien. Por ejemplo, no todos los espacios métricos finitos se pueden incrustar isométricamente en un espacio euclidiano o en un espacio de Hilbert . Por otro lado, en el peor de los casos la distorsión requerida (constante de bilipschitz) es solo logarítmica en el número de puntos. ^{[24] [25]}

Para cualquier grafo conexo no dirigido G , el conjunto V de vértices de G se puede convertir en un espacio métrico definiendo la distancia entre los vértices x e y como la longitud del camino de arista más corto que los conecta. Esto también se llama distancia del camino más corto o distancia geodésica . En la teoría de grupos geométricos, esta construcción se aplica al grafo de Cayley de un grupo finitamente generado (normalmente infinito) , lo que da lugar a la palabra métrica . Hasta un homeomorfismo bilipschitz, la palabra métrica depende solo del grupo y no del conjunto generador finito elegido. ^[15]

Distancias entre objetos matemáticos

En las matemáticas modernas, se estudian a menudo espacios cuyos puntos son en sí mismos objetos matemáticos. Una función de distancia en un espacio de este tipo generalmente tiene como objetivo medir la disimilitud entre dos objetos. A continuación se ofrecen algunos ejemplos:

• Funciones en un espacio métrico. Si X es un conjunto cualquiera y M es un espacio métrico, entonces el conjunto de todas las funciones acotadas (es decir, aquellas funciones cuya imagen es un subconjunto acotado de ) se puede convertir en un espacio métrico definiendo la distancia entre dos funciones acotadas f y g como Esta métrica se denomina métrica uniforme o métrica suprema. ^[26] Si M es completo, entonces este espacio funcional también es completo; además, si X es también un espacio topológico, entonces el subespacio que consiste en todas las funciones continuas acotadas desde X hasta M también es completo. Cuando X es un subespacio de , este espacio funcional se conoce como espacio clásico de Wiener . ${\displaystyle f\colon X\to M}$ ${\displaystyle M}$ $${\displaystyle d(f,g)=\sup _{x\in X}d(f(x),g(x)).}$$ ${\displaystyle \mathbb {R} ^{n}}$
• Métricas de cadenas y distancias de edición . Existen muchas formas de medir distancias entre cadenas de caracteres , que pueden representar oraciones en lingüística computacional o palabras clave en teoría de codificación . Las distancias de edición intentan medir la cantidad de cambios necesarios para pasar de una cadena a otra. Por ejemplo, la distancia de Hamming mide la cantidad mínima de sustituciones necesarias, mientras que la distancia de Levenshtein mide la cantidad mínima de eliminaciones, inserciones y sustituciones; ambas pueden considerarse como distancias en un gráfico apropiado.
• La distancia de edición de gráficos es una medida de disimilitud entre dos gráficos , definida como el número mínimo de operaciones de edición de gráficos necesarias para transformar un gráfico en otro.
• Las métricas de Wasserstein miden la distancia entre dos medidas en el mismo espacio métrico. La distancia de Wasserstein entre dos medidas es, en términos generales, el costo de transportar una a la otra.
• El conjunto de todas las matrices m por n sobre algún campo es un espacio métrico con respecto a la distancia de rango . ${\displaystyle d(A,B)=\mathrm {rank} (B-A)}$
• La métrica Helly en la teoría de juegos mide la diferencia entre estrategias en un juego.

Distancia de Hausdorff y Gromov–Hausdorff

La idea de espacios de objetos matemáticos también se puede aplicar a subconjuntos de un espacio métrico, así como a los propios espacios métricos. La distancia de Hausdorff y la distancia de Gromov-Hausdorff definen métricas en el conjunto de subconjuntos compactos de un espacio métrico y en el conjunto de espacios métricos compactos, respectivamente.

Supóngase que ( M , d ) es un espacio métrico, y sea S un subconjunto de M . La distancia desde S a un punto x de M es, informalmente, la distancia desde x al punto más cercano de S . Sin embargo, dado que puede no haber un único punto más cercano, se define mediante un ínfimo : En particular, si y solo si x pertenece a la clausura de S . Además, las distancias entre puntos y conjuntos satisfacen una versión de la desigualdad triangular: y por lo tanto la función definida por es continua. Por cierto, esto demuestra que los espacios métricos son completamente regulares . $${\displaystyle d(x,S)=\inf\{d(x,s):s\in S\}.}$$ ${\displaystyle d(x,S)=0}$ $${\displaystyle d(x,S)\leq d(x,y)+d(y,S),}$$ ${\displaystyle d_{S}:M\to \mathbb {R} }$ ${\displaystyle d_{S}(x)=d(x,S)}$

Dados dos subconjuntos S y T de M , su distancia de Hausdorff es De manera informal, dos conjuntos S y T están cerca uno del otro en la distancia de Hausdorff si ningún elemento de S está demasiado lejos de T y viceversa. Por ejemplo, si S es un conjunto abierto en el espacio euclidiano T es una ε-red dentro de S , entonces . En general, la distancia de Hausdorff puede ser infinita o cero. Sin embargo, la distancia de Hausdorff entre dos conjuntos compactos distintos es siempre positiva y finita. Por lo tanto, la distancia de Hausdorff define una métrica en el conjunto de subconjuntos compactos de M . $${\displaystyle d_{H}(S,T)=\max\{\sup\{d(s,T):s\in S\},\sup\{d(t,S):t\in T\}\}.}$$ ${\displaystyle d_{H}(S,T)<\varepsilon }$ ${\displaystyle d_{H}(S,T)}$

La métrica de Gromov-Hausdorff define una distancia entre (clases de isometría de) espacios métricos compactos. La distancia de Gromov-Hausdorff entre espacios compactos X e Y es el ínfimo de la distancia de Hausdorff sobre todos los espacios métricos Z que contienen X e Y como subespacios. Si bien rara vez resulta útil conocer el valor exacto de la distancia de Gromov-Hausdorff, la topología resultante ha encontrado muchas aplicaciones.

Ejemplos varios

• Dado un espacio métrico ( X , d ) y una función cóncava creciente tal que f ( t ) = 0 si y sólo si t = 0 , entonces también es una métrica en X . Si f ( t ) = t ^α para algún número real α < 1 , dicha métrica se conoce como un copo de nieve de d . ^[27] ${\displaystyle f\colon [0,\infty )\to [0,\infty )}$ ${\displaystyle d_{f}(x,y)=f(d(x,y))}$
• El estrecho espacio de un espacio métrico es otro espacio métrico que puede considerarse como una versión abstracta de la envoltura convexa .
• La métrica de movimiento del caballo , el número mínimo de movimientos del caballo para llegar a un punto desde otro, es una métrica en . ${\displaystyle \mathbb {Z} ^{2}}$ ${\displaystyle \mathbb {Z} ^{2}}$
• La métrica de British Rail (también llamada "métrica de la oficina postal" o "métrica de la SNCF ") en un espacio vectorial normalizado está dada por para puntos distintos y , y . De manera más general, se puede reemplazar con una función que tome un conjunto arbitrario de reales no negativos y tome el valor como máximo una vez: entonces la métrica se define en por para puntos distintos y , y . El nombre alude a la tendencia de los viajes en tren a pasar por Londres (o París) independientemente de su destino final. ${\displaystyle d(x,y)=\lVert x\rVert +\lVert y\rVert }$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle d(x,x)=0}$ ${\displaystyle \lVert \cdot \rVert }$ ${\displaystyle f}$ ${\displaystyle S}$ ${\displaystyle 0}$ ${\displaystyle S}$ ${\displaystyle d(x,y)=f(x)+f(y)}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle d(x,x)=0}$
• La métrica de Robinson-Foulds utilizada para calcular las distancias entre árboles filogenéticos en filogenética ^[28]

Construcciones

Espacios métricos de productos

Si son espacios métricos, y N es la norma euclidiana en , entonces es un espacio métrico, donde la métrica del producto está definida por y la topología inducida concuerda con la topología del producto . Por la equivalencia de normas en dimensiones finitas, se obtiene una métrica topológicamente equivalente si N es la norma del taxi , una p-norma , la norma máxima o cualquier otra norma que no sea decreciente a medida que aumentan las coordenadas de una n -tupla positiva (lo que produce la desigualdad triangular). ${\displaystyle (M_{1},d_{1}),\ldots ,(M_{n},d_{n})}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle {\bigl (}M_{1}\times \cdots \times M_{n},d_{\times }{\bigr )}}$ $${\displaystyle d_{\times }{\bigl (}(x_{1},\ldots ,x_{n}),(y_{1},\ldots ,y_{n}){\bigr )}=N{\bigl (}d_{1}(x_{1},y_{1}),\ldots ,d_{n}(x_{n},y_{n}){\bigr )},}$$

De manera similar, se puede obtener una métrica del producto topológico de un número contable de espacios métricos utilizando la métrica $${\displaystyle d(x,y)=\sum _{i=1}^{\infty }{\frac {1}{2^{i}}}{\frac {d_{i}(x_{i},y_{i})}{1+d_{i}(x_{i},y_{i})}}.}$$

El producto topológico de un número incontable de espacios métricos no tiene por qué ser metrizable. Por ejemplo, un producto incontable de copias de no es primero contable y, por lo tanto, no es metrizable. ${\displaystyle \mathbb {R} }$

Espacios métricos cociente

Si M es un espacio métrico con métrica d , y es una relación de equivalencia en M , entonces podemos dotar al conjunto cociente de una pseudométrica. La distancia entre dos clases de equivalencia y se define como donde el ínfimo se toma sobre todas las sucesiones finitas y con , , . ^[29] En general, esto solo definirá una pseudométrica , es decir, no implica necesariamente que . Sin embargo, para algunas relaciones de equivalencia (por ejemplo, las que se dan al pegar poliedros a lo largo de las caras), es una métrica. ${\displaystyle \sim }$ ${\displaystyle M/\!\sim }$ ${\displaystyle [x]}$ ${\displaystyle [y]}$ $${\displaystyle d'([x],[y])=\inf\{d(p_{1},q_{1})+d(p_{2},q_{2})+\dotsb +d(p_{n},q_{n})\},}$$ ${\displaystyle (p_{1},p_{2},\dots ,p_{n})}$ ${\displaystyle (q_{1},q_{2},\dots ,q_{n})}$ ${\displaystyle p_{1}\sim x}$ ${\displaystyle q_{n}\sim y}$ ${\displaystyle q_{i}\sim p_{i+1},i=1,2,\dots ,n-1}$ ${\displaystyle d'([x],[y])=0}$ ${\displaystyle [x]=[y]}$ ${\displaystyle d'}$

La métrica del cociente se caracteriza por la siguiente propiedad universal . Si es una función métrica (es decir, 1-Lipschitz) entre espacios métricos que satisface f ( x ) = f ( y ) siempre que , entonces la función inducida , dada por , es una función métrica ${\displaystyle d'}$ ${\displaystyle f\,\colon (M,d)\to (X,\delta )}$ ${\displaystyle x\sim y}$ ${\displaystyle {\overline {f}}\,\colon {M/\sim }\to X}$ ${\displaystyle {\overline {f}}([x])=f(x)}$ ${\displaystyle {\overline {f}}\,\colon (M/\sim ,d')\to (X,\delta ).}$

La métrica del cociente no siempre induce la topología del cociente . Por ejemplo, el cociente topológico del espacio métrico que identifica todos los puntos de la forma no es metrizable ya que no es numerable en primer lugar , pero la métrica del cociente es una métrica bien definida en el mismo conjunto que induce una topología más burda . Además, diferentes métricas en el espacio topológico original (una unión disjunta de un número numerable de intervalos) conducen a diferentes topologías en el cociente. ^[30] ${\displaystyle \mathbb {N} \times [0,1]}$ ${\displaystyle (n,0)}$

Un espacio topológico es secuencial si y sólo si es un cociente (topológico) de un espacio métrico. ^[31]

Generalizaciones de espacios métricos

Hay varias nociones de espacios que tienen menos estructura que un espacio métrico, pero más que un espacio topológico.

• Los espacios uniformes son espacios en los que no están definidas distancias, pero sí la continuidad uniforme.
• Los espacios de aproximación son espacios en los que se definen distancias de punto a conjunto, en lugar de distancias de punto a punto. Tienen propiedades particularmente buenas desde el punto de vista de la teoría de categorías .
• Los espacios de continuidad son una generalización de los espacios métricos y posets que pueden utilizarse para unificar las nociones de espacios métricos y dominios .

También existen numerosas formas de relajar los axiomas de una métrica, lo que da lugar a diversas nociones de espacios métricos generalizados. Estas generalizaciones también se pueden combinar. La terminología utilizada para describirlas no está completamente estandarizada. En particular, en el análisis funcional las pseudometrías a menudo provienen de seminormas en espacios vectoriales, por lo que es natural llamarlas "semimetrías". Esto entra en conflicto con el uso del término en topología .

Métricas extendidas

Algunos autores definen las métricas de modo que permitan que la función de distancia d alcance el valor ∞, es decir, las distancias son números no negativos en la línea de números reales extendida . ^[4] Una función de este tipo también se denomina métrica extendida o "∞-métrica". Cada métrica extendida puede reemplazarse por una métrica de valor real que sea topológicamente equivalente. Esto se puede hacer utilizando una función acotada monótonamente creciente subaditiva que sea cero en cero, por ejemplo o . ${\displaystyle d'(x,y)=d(x,y)/(1+d(x,y))}$ ${\displaystyle d''(x,y)=\min(1,d(x,y))}$

Métricas valoradas en estructuras distintas a los números reales

El requisito de que la métrica tome valores se puede flexibilizar para considerar métricas con valores en otras estructuras, entre ellas: ${\displaystyle [0,\infty )}$

• Campos ordenados , que dan lugar a la noción de una métrica generalizada .
• Conjuntos dirigidos más generales . En ausencia de una operación de adición, la desigualdad triangular no tiene sentido y se reemplaza por una desigualdad ultramétrica . Esto conduce a la noción de una desigualdad ultramétrica generalizada . ^[32]

Estas generalizaciones todavía inducen una estructura uniforme en el espacio.

Pseudometría

Una pseudométrica es una función que satisface los axiomas para una métrica, excepto que en lugar del segundo (identidad de indiscernibles) se requiere solo para todos . ^[33] En otras palabras, los axiomas para una pseudométrica son: ${\displaystyle X}$ ${\displaystyle d:X\times X\to \mathbb {R} }$ ${\displaystyle d(x,x)=0}$ ${\displaystyle x}$

1. ${\displaystyle d(x,y)\geq 0}$
2. ${\displaystyle d(x,x)=0}$
3. ${\displaystyle d(x,y)=d(y,x)}$
4. ${\displaystyle d(x,z)\leq d(x,y)+d(y,z)}$.

En algunos contextos, las pseudometrías se denominan semimetrías ^[34] debido a su relación con las seminormas .

Cuasimetría

Ocasionalmente, una cuasimetrica se define como una función que satisface todos los axiomas de una métrica con la posible excepción de la simetría. ^[35] El nombre de esta generalización no está completamente estandarizado. ^[36]

1. ${\displaystyle d(x,y)\geq 0}$
2. ${\displaystyle d(x,y)=0\iff x=y}$
3. ${\displaystyle d(x,z)\leq d(x,y)+d(y,z)}$

Los cálculos cuasimétricos son comunes en la vida real. Por ejemplo, dado un conjunto X de pueblos de montaña, los tiempos típicos de caminata entre elementos de X forman un cálculo cuasimétrico porque el viaje cuesta arriba lleva más tiempo que el viaje cuesta abajo. Otro ejemplo es la duración de los viajes en automóvil en una ciudad con calles de un solo sentido: aquí, un camino más corto del punto A al punto B pasa por un conjunto de calles diferente al camino más corto del B al A y puede tener una longitud diferente.

Una cuasimétrica sobre los números reales se puede definir estableciendo El 1 puede reemplazarse, por ejemplo, por infinito o por o cualquier otra función subaditiva de y - x . Esta cuasimétrica describe el costo de modificar una barra de metal: es fácil reducir su tamaño limándola , pero es difícil o imposible hacerla crecer. $${\displaystyle d(x,y)={\begin{cases}x-y&{\text{if }}x\geq y,\\1&{\text{otherwise.}}\end{cases}}}$$ ${\displaystyle 1+{\sqrt {y-x}}}$

Dado un cuasimetrico en X , se puede definir una R -bola alrededor de x como el conjunto . Como en el caso de una métrica, dichas bolas forman una base para una topología en X , pero esta topología no necesita ser metrizable. Por ejemplo, la topología inducida por el cuasimetrico en los números reales descritos anteriormente es la línea de Sorgenfrey (invertida) . ${\displaystyle \{y\in X|d(x,y)\leq R\}}$

Metametría o métricas parciales

En una metamétrica se cumplen todos los axiomas de una métrica, excepto que la distancia entre puntos idénticos no es necesariamente cero. En otras palabras, los axiomas de una metamétrica son:

1. ${\displaystyle d(x,y)\geq 0}$
2. ${\displaystyle d(x,y)=0\implies x=y}$
3. ${\displaystyle d(x,y)=d(y,x)}$
4. ${\displaystyle d(x,z)\leq d(x,y)+d(y,z).}$

La metametría aparece en el estudio de los espacios métricos hiperbólicos de Gromov y sus límites. La metametría visual en un espacio de este tipo satisface para los puntos en el límite, pero en el resto de los casos es aproximadamente la distancia desde el límite hasta el límite. La metametría fue definida por primera vez por Jussi Väisälä. ^[37] En otros trabajos, una función que satisface estos axiomas se denomina métrica parcial ^{[38] [39]} o métrica dislocada . ^[33] ${\displaystyle d(x,x)=0}$ ${\displaystyle x}$ ${\displaystyle d(x,x)}$ ${\displaystyle x}$

Semimetría

Una función semimétrica es una función que satisface los primeros tres axiomas, pero no necesariamente la desigualdad triangular: ${\displaystyle X}$ ${\displaystyle d:X\times X\to \mathbb {R} }$

1. ${\displaystyle d(x,y)\geq 0}$
2. ${\displaystyle d(x,y)=0\iff x=y}$
3. ${\displaystyle d(x,y)=d(y,x)}$

Algunos autores trabajan con una forma más débil de la desigualdad triangular, como:

La desigualdad ρ-inframétrica implica la desigualdad triangular ρ-relajada (asumiendo el primer axioma), y la desigualdad triangular ρ-relajada implica la desigualdad 2ρ-inframétrica. Las semimétricas que satisfacen estas condiciones equivalentes a veces se han denominado cuasimetrías ^[40] , casimétricas ^[41] o inframétricas ^[42] .

Las desigualdades ρ-inframétricas se introdujeron para modelar los tiempos de retardo de ida y vuelta en Internet . ^[42] La desigualdad triangular implica la desigualdad 2-inframétrica, y la desigualdad ultramétrica es exactamente la desigualdad 1-inframétrica.

Premétricas

La relajación de los tres últimos axiomas conduce a la noción de premétrica , es decir, una función que satisface las siguientes condiciones:

1. ${\displaystyle d(x,y)\geq 0}$
2. ${\displaystyle d(x,x)=0}$

Este no es un término estándar. A veces se utiliza para referirse a otras generalizaciones de métricas como pseudosemimetría ^[43] o pseudometría; ^[44] en traducciones de libros rusos a veces aparece como "pramétrica". ^[45] Una premétrica que satisface la simetría, es decir, una pseudosemimetría, también se denomina distancia. ^[46]

Cualquier premétrica da lugar a una topología como la siguiente. Para un real positivo , la bola centrada en un punto se define como ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle p}$

${\displaystyle B_{r}(p)=\{x|d(x,p)<r\}.}$

Un conjunto se llama abierto si para cualquier punto del conjunto hay una bola centrada en la cual está contenida en el conjunto. Todo espacio premétrico es un espacio topológico, y de hecho un espacio secuencial . En general, las bolas mismas no necesitan ser conjuntos abiertos con respecto a esta topología. En cuanto a las métricas, la distancia entre dos conjuntos y , se define como ${\displaystyle p}$ ${\displaystyle r}$ ${\displaystyle p}$ ${\displaystyle r}$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle d(A,B)={\underset {x\in A,y\in B}{\inf }}d(x,y).}$

Esto define una premétrica en el conjunto potencia de un espacio premétrico. Si comenzamos con un espacio (pseudosemi)métrico, obtenemos una premétrica pseudosemimétrica, es decir, simétrica. Cualquier premétrica da lugar a un operador de preclausura como sigue: ${\displaystyle cl}$

${\displaystyle cl(A)=\{x|d(x,A)=0\}.}$

Pseudocuasimetría

Los prefijos pseudo- , cuasi- y semi- también se pueden combinar, por ejemplo, un pseudocuasimétrico (a veces llamado hemimétrico ) relaja tanto el axioma de indiscernibilidad como el axioma de simetría y es simplemente un premétrico que satisface la desigualdad del triángulo. Para espacios pseudocuasimétricos, las bolas abiertas forman una base de conjuntos abiertos. Un ejemplo muy básico de un espacio pseudocuasimétrico es el conjunto con el premétrico dado por y El espacio topológico asociado es el espacio de Sierpiński . ${\displaystyle r}$ ${\displaystyle \{0,1\}}$ ${\displaystyle d(0,1)=1}$ ${\displaystyle d(1,0)=0.}$

Los conjuntos equipados con un pseudoquasimétrico extendido fueron estudiados por William Lawvere como "espacios métricos generalizados". ^[47] Desde un punto de vista categórico , los espacios pseudométricos extendidos y los espacios pseudoquasimétricos extendidos, junto con sus correspondientes funciones no expansivas, son las categorías de espacio métrico que mejor se comportan . Se pueden tomar productos y coproductos arbitrarios y formar objetos cocientes dentro de la categoría dada. Si se omite "extendido", solo se pueden tomar productos y coproductos finitos. Si se omite "pseudo", no se pueden tomar cocientes.

Lawvere también dio una definición alternativa de dichos espacios como categorías enriquecidas . El conjunto ordenado puede verse como una categoría con un morfismo si y ninguno en caso contrario. El uso de + como producto tensorial y 0 como identidad convierte a esta categoría en una categoría monoidal . Todo espacio pseudocuasi-métrico (extendido) puede verse ahora como una categoría enriquecida con : ${\displaystyle (\mathbb {R} ,\geq )}$ ${\displaystyle a\to b}$ ${\displaystyle a\geq b}$ ${\displaystyle R^{*}}$ ${\displaystyle (M,d)}$ ${\displaystyle M^{*}}$ ${\displaystyle R^{*}}$

• Los objetos de la categoría son los puntos de M .
• Para cada par de puntos x e y tales que , hay un único morfismo al que se le asigna el objeto de . ${\displaystyle d(x,y)<\infty }$ ${\displaystyle d(x,y)}$ ${\displaystyle R^{*}}$
• La desigualdad triangular y el hecho de que para todos los puntos x se derivan de las propiedades de composición e identidad en una categoría enriquecida. ${\displaystyle d(x,x)=0}$
• Dado que es un conjunto posesivo, todos los diagramas necesarios para una categoría enriquecida conmutan automáticamente. ${\displaystyle R^{*}}$

Métricas en conjuntos múltiples

La noción de métrica se puede generalizar a partir de una distancia entre dos elementos a un número asignado a un multiconjunto de elementos. Un multiconjunto es una generalización de la noción de conjunto en el que un elemento puede aparecer más de una vez. Defina la unión de multiconjuntos de la siguiente manera: si un elemento x aparece m veces en X y n veces en Y , entonces aparece m + n veces en U. Una función d en el conjunto de multiconjuntos finitos no vacíos de elementos de un conjunto M es una métrica ^[48] si ${\displaystyle U=XY}$

1. ${\displaystyle d(X)=0}$si todos los elementos de X son iguales y en caso contrario ( definición positiva ) ${\displaystyle d(X)>0}$
2. ${\displaystyle d(X)}$depende únicamente del multiconjunto (desordenado) X ( simetría )
3. ${\displaystyle d(XY)\leq d(XZ)+d(ZY)}$( desigualdad triangular )

Considerando los casos de los axiomas 1 y 2 en los que el multiconjunto X tiene dos elementos y el caso del axioma 3 en el que los multiconjuntos X , Y y Z tienen un elemento cada uno, se recuperan los axiomas usuales para una métrica. Es decir, toda métrica de multiconjunto produce una métrica ordinaria cuando se restringe a conjuntos de dos elementos.

Un ejemplo simple es el conjunto de todos los multiconjuntos finitos no vacíos de números enteros con . Ejemplos más complejos son la distancia de información en multiconjuntos; ^[48] y la distancia de compresión normalizada (NCD) en multiconjuntos. ^[49] ${\displaystyle X}$ ${\displaystyle d(X)=\max(X)-\min(X)}$

Véase también

• Métrica acústica  : Tensor que caracteriza las propiedades de transmisión de señales en un medio
• Espacio métrico completo  – Geometría métrica
• Diversidad (matemáticas)  – Generalización de espacios métricos
• Espacio métrico generalizado
• Cuarto problema de Hilbert  : Construir todos los espacios métricos donde las líneas se asemejen a las de una esfera
• Árbol métrico
• Distancia de Minkowski  : métrica matemática en el espacio vectorial normalizado
• Función de distancia con signo  : distancia desde un punto hasta el límite de un conjunto
• Medida de similitud  : función de valor real que cuantifica la similitud entre dos objetos.
• Espacio (matemáticas)  : conjunto matemático con cierta estructura añadida
• Espacio ultramétrico  – Tipo de espacio métrico

Notas

1. Las bolas con radio racional alrededor de un punto x forman una base de vecindad para ese punto.
2. En el contexto de los intervalos en la línea real, o más generalmente en las regiones del espacio euclidiano, los conjuntos acotados a veces se denominan "intervalos finitos" o "regiones finitas". Sin embargo, no suelen tener un número finito de elementos y, si bien todos tienen un volumen finito , también lo tienen muchos conjuntos no acotados. Por lo tanto, esta terminología es imprecisa.
3. Esto difiere del uso en la geometría de Riemann , donde las geodésicas son solo rutas localmente más cortas. Algunos autores definen las geodésicas en espacios métricos de la misma manera. ^{[18] [19]}

Citas

1. Čech 1969, pág. 42.
2. Burago, Burago e Ivanov 2001.
3. Heinonen 2001.
4. Burago, Burago e Ivanov 2001, p. 1.
5. Gromov 2007, pág. xv.
6. Gleason, Andrew (1991). Fundamentos del análisis abstracto (1.ª ed.). Taylor & Francis . pág. 223. doi :10.1201/9781315275444. ISBN . 9781315275444.S2CID62222843  .​
7. Fréchet, M. (diciembre de 1906). "Sobre los puntos del cálculo funcional". Rendiconti del Circolo Matematico di Palermo . 22 (1): 1–72. doi :10.1007/BF03018603. S2CID  123251660.
8. F. Hausdorff (1914) Grundzuge der Mengenlehre
9. Blumberg, Henry (1927). "Grundzüge der Mengenlehre de Hausdorff". Boletín de la Sociedad Matemática Estadounidense . 6 : 778–781. doi : 10.1090/S0002-9904-1920-03378-1 .
10. Mohamed A. Khamsi y William A. Kirk (2001) Introducción a los espacios métricos y la teoría del punto fijo , página 14, John Wiley & Sons
11. Rudin, Mary Ellen. Una nueva prueba de que los espacios métricos son paracompactos Archivado el 12 de abril de 2016 en Wayback Machine . Proceedings of the American Mathematical Society, vol. 20, n.º 2. (febrero de 1969), pág. 603.
12. Burago, Burago e Ivanov 2001, pág. 2.
13. Burago, Burago & Ivanov 2001, p. 2.
    Algunos autores se refieren a cualquier función que preserva la distancia como una isometría, por ejemplo Munkres 2000, p. 181.
14. Gromov 2007, pág. xvii.
15. Margalit y Thomas 2017.
16. Narici y Beckenstein 2011, págs. 47–66.
17. Burago, Burago e Ivanov 2001, Definición 2.3.1.
18. Burago, Burago e Ivanov 2001, Definición 2.5.27.
19. Gromov 2007, Definición 1.9.
20. Burago, Burago e Ivanov 2001, pág. 127.
21. Heinonen 2007, pág. 191.
22. Gigli, Nicola (18 de octubre de 2018). "Apuntes de clase sobre cálculo diferencial en espacios RCD". Publicaciones del Instituto de Investigación en Ciencias Matemáticas . 54 (4): 855–918. arXiv : 1703.06829 . doi :10.4171/PRIMS/54-4-4. S2CID  119129867.
23. Linial, Nathan (2003). "Espacios métricos finitos: combinatoria, geometría y algoritmos". Actas del ICM, Pekín 2002. Vol. 3. págs. 573–586. arXiv : math/0304466 .
24. Bourgain, J. (1985). "Sobre la incrustación de Lipschitz de espacios métricos finitos en el espacio de Hilbert". Revista israelí de matemáticas . 52 (1–2): 46–52. doi :10.1007/BF02776078. S2CID  121649019.
25. Jiří Matoušek y Assaf Naor , ed. "Problemas abiertos sobre incrustaciones de espacios métricos finitos". Archivado el 26 de diciembre de 2010 en Wayback Machine .
26. Ó Searcóid 2006, pág. 107.
27. Gottlieb, Lee-Ad; Solomon, Shay (8 de junio de 2014). Llaves de luz para métricas de copos de nieve . SOCG '14: Actas del trigésimo simposio anual sobre geometría computacional. págs. 387–395. arXiv : 1401.5014 . doi :10.1145/2582112.2582140.
28. Robinson, DF; Foulds, LR (febrero de 1981). "Comparación de árboles filogenéticos" . Ciencias biológicas matemáticas . 53 (1–2): 131–147. doi :10.1016/0025-5564(81)90043-2. ​​S2CID  121156920.
29. Burago, Burago e Ivanov 2001, Definición 3.1.12.
30. Véase Burago, Burago e Ivanov 2001, Ejemplo 3.1.17, aunque en este libro se afirma incorrectamente que el cociente es homeomorfo al cociente topológico. ${\displaystyle \mathbb {N} \times [0,1]/\mathbb {N} \times \{0\}}$
31. Goreham, Anthony. Convergencia secuencial en espacios topológicos Archivado el 4 de junio de 2011 en Wayback Machine . Tesis de grado, Queen's College, Oxford (abril de 2001), pág. 14
32. Hitzler & Seda 2016, Definición 4.3.1.
33. Hitzler & Seda 2016, Definición 4.2.1.
34. Burago, Burago e Ivanov 2001, Definición 1.1.4.
35. Steen y Seebach (1995); Smyth (1988)
36. Rolewicz (1987) las denomina "semimétricas". Ese mismo término también se utiliza con frecuencia para otras dos generalizaciones de las métricas.
37. Väisälä 2005.
38. "Métricas parciales: bienvenidas". www.dcs.warwick.ac.uk . Archivado desde el original el 27 de julio de 2017 . Consultado el 2 de mayo de 2018 .
39. Bukatin, Michael; Kopperman, Ralph; Matthews, Steve; Pajoohesh, Homeira (1 de octubre de 2009). "Espacios métricos parciales" (PDF) . American Mathematical Monthly . 116 (8): 708–718. doi :10.4169/193009709X460831. S2CID  13969183.
40. Xia 2009.
41. Xia 2008.
42. Fraigniaud, Lebhar y Viennot 2008.
43. Buldygin y Kozachenko 2000.
44. Helemskii 2006.
45. Arkhangel'skii y Pontryagin (1990); Aldrovandi y Pereira (2017)
46. Deza y Laurent 1997.
47. Lawvere (1973); Vickers (2005)
48. Vitányi 2011.
49. Cohen y Vitányi 2012.

Referencias

• Aldrovandi, Rubén; Pereira, José Geraldo (2017), Introducción a la física geométrica (2ª ed.), Hackensack, Nueva Jersey: World Scientific, p. 20, ISBN 978-981-3146-81-5, Sr.  3561561
• Arkhangelskii, AV ; Pontryagin, LS (1990), Topología general I: conceptos básicos y construcciones Teoría de la dimensión , Enciclopedia de ciencias matemáticas, Springer , ISBN 3-540-18178-4
• Bryant, Victor (1985). Espacios métricos: iteración y aplicación . Cambridge University Press. ISBN 0-521-31897-1.
• Buldygin, VV; Kozachenko, Yu. V. (2000), Caracterización métrica de variables aleatorias y procesos aleatorios , Traducciones de monografías matemáticas, vol. 188, Providence, Rhode Island: American Mathematical Society, p. 129, doi : 10.1090/mmono/188, ISBN 0-8218-0533-9, Sr.  1743716
• Burago, Dmitri ; Burago, Yuri ; Ivanov, Sergei (2001). Un curso de geometría métrica . Providence, RI: Sociedad Estadounidense de Matemáticas. ISBN 0-8218-2129-6.
• Čech, Eduard (1969). Conjuntos de puntos . Academic Press. ISBN 0121648508.
• Cohen, Andrew R.; Vitányi, Paul MB (2012), "Distancia de compresión normalizada de conjuntos múltiples con aplicaciones", IEEE Transactions on Pattern Analysis and Machine Intelligence , 37 (8): 1602–1614, arXiv : 1212.5711 , doi :10.1109/TPAMI.2014.2375175, PMC  4566858 , PMID  26352998
• Deza, Michel Marie ; Laurent, Monique (1997), Geometría de cortes y métricas, Algoritmos y combinatoria, vol. 15, Springer-Verlag, Berlín, p. 27, doi :10.1007/978-3-642-04295-9, ISBN 3-540-61611-X, Sr.  1460488
• Fraigniaud, P.; Lebhar, E.; Viennot, L. (2008), "El modelo inframétrico para Internet", 2008 IEEE INFOCOM - La 27.ª Conferencia sobre Comunicaciones Informáticas , pp. 1085–1093, CiteSeerX  10.1.1.113.6748 , doi :10.1109/INFOCOM.2008.163, ISBN 978-1-4244-2026-1, Número de identificación del sujeto  5733968
• Gromov, Mikhael (2007). Estructuras métricas para espacios riemannianos y no riemannianos . Boston: Birkhäuser. ISBN 978-0-8176-4582-3.
• Heinonen, Juha (2001). Lecciones sobre análisis de espacios métricos . Nueva York: Springer. ISBN 0-387-95104-0.
• Heinonen, Juha (24 de enero de 2007). "Cálculo no uniforme". Boletín de la Sociedad Matemática Americana . 44 (2): 163–232. doi : 10.1090/S0273-0979-07-01140-8 .
• Helemskii, A. Ya. (2006), Lecciones y ejercicios sobre análisis funcional, Traducciones de monografías matemáticas, vol. 233, Providence, Rhode Island: American Mathematical Society, pág. 14, doi : 10.1090/mmono/233 , ISBN 978-0-8218-4098-6, Sr.  2248303
• Hitzler, Pascal ; Seda, Anthony (19 de abril de 2016). Aspectos matemáticos de la semántica de la programación lógica. CRC Press. hdl :20.500.12657/40111. ISBN 978-1-4398-2962-2.
• Lawvere, F. William (diciembre de 1973). "Espacios métricos, lógica generalizada y categorías cerradas". Rediconti del Seminario Matematico e Fisico di Milano . 43 (1): 135-166. doi :10.1007/BF02924844. S2CID  1845177.
• Margalit, Dan ; Thomas, Anne (2017). "Hora de oficina 7. Cuasi-isometrías". Horas de oficina con un teórico de grupos geométricos . Princeton University Press. págs. 125–145. ISBN 978-1-4008-8539-8.JSTOR j.ctt1vwmg8g.11  .
• Munkres, James R. (2000). Topología (segunda edición). Upper Saddle River, NJ : Prentice Hall, Inc. ISBN 978-0-13-181629-9.OCLC 42683260  .
• Narici, Lawrence; Beckenstein, Edward (2011), Espacios vectoriales topológicos , Matemáticas puras y aplicadas (segunda edición), Boca Raton, FL: CRC Press, ISBN 978-1584888666, OCLC  144216834
• Ó Searcóid, Mícheál (2006). Espacios métricos . Londres: Springer. ISBN 1-84628-369-8.
• Papadopoulos, Athanase (2014). Espacios métricos, convexidad y curvatura no positiva (segunda edición). Zúrich, Suiza: European Mathematical Society . ISBN 978-3-03719-132-3.
• Rolewicz, Stefan (1987). Análisis funcional y teoría del control: sistemas lineales . Springer . ISBN. 90-277-2186-6.
• Rudin, Walter (1976). Principios del análisis matemático (tercera edición). Nueva York: McGraw-Hill. ISBN 0-07-054235-X.OCLC 1502474  .
• Smyth, M. (1988), "Uniformidades cuasi: reconciliación de dominios con espacios métricos", en Main, M.; Melton, A.; Mislove, M.; Schmidt, D. (eds.), Fundamentos matemáticos de la semántica de lenguajes de programación , Lecture Notes in Computer Science, vol. 298, Springer-Verlag, págs. 236–253, doi :10.1007/3-540-19020-1_12, ISBN 978-3-540-19020-2
• Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978]. Contraejemplos en topología . Dover . ISBN 978-0-486-68735-3.Sr. 0507446  .
• Vitányi, Paul MB (2011). "Distancia de información en múltiplos". IEEE Transactions on Information Theory . 57 (4): 2451–2456. arXiv : 0905.3347 . doi :10.1109/TIT.2011.2110130. S2CID  6302496.
• Väisälä, Jussi (2005). "Espacios hiperbólicos de Gromov" (PDF) . Exposiciones Mathematicae . 23 (3): 187–231. doi : 10.1016/j.exmath.2005.01.010 . SEÑOR  2164775.
• Vickers, Steven (2005). "Completar localmente espacios métricos generalizados, I". Teoría y aplicaciones de categorías . 14 (15): 328–356. MR  2182680.
• Weisstein, Eric W. "Métrica del producto". MathWorld .
• Xia, Qinglan (2008). "El problema geodésico en espacios casi métricos". Revista de análisis geométrico . 19 (2): 452–479. arXiv : 0807.3377 . doi :10.1007/s12220-008-9065-4. S2CID  17475581.
• Xia, Q. (2009). "El problema geodésico en espacios cuasimétricos". Journal of Geometric Analysis . 19 (2): 452–479. arXiv : 0807.3377 . doi :10.1007/s12220-008-9065-4. S2CID  17475581.

Enlaces externos

• "Espacio métrico", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Lejos y cerca: varios ejemplos de funciones de distancia en el momento de cortar el nudo .