Aberración (astronomía)

Fenómeno en el que los objetos parecen moverse respecto a sus posiciones reales en el cielo.

Diagrama que muestra cómo la posición aparente de una estrella vista desde la Tierra puede cambiar según la velocidad de la Tierra. El efecto suele ser mucho menor que el ilustrado.

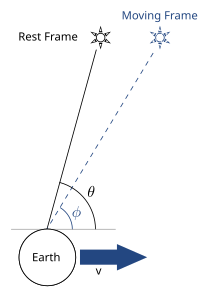
En astronomía , la aberración (también denominada aberración astronómica , aberración estelar o aberración de velocidad ) es un fenómeno en el que los objetos celestes exhiben un movimiento aparente sobre sus posiciones reales en función de la velocidad del observador: hace que los objetos parezcan estar desplazados hacia la dirección de movimiento del observador. El cambio de ángulo es del orden de donde es la velocidad de la luz y la velocidad del observador. En el caso de la aberración "estelar" o "anual", la posición aparente de una estrella para un observador en la Tierra varía periódicamente a lo largo de un año a medida que cambia la velocidad de la Tierra a medida que gira alrededor del Sol, en un ángulo máximo de aproximadamente 20  segundos de arco en ascensión recta o declinación . ${\displaystyle v/c}$ ${\displaystyle c}$ ${\displaystyle v}$

El término aberración se ha utilizado históricamente para referirse a una serie de fenómenos relacionados con la propagación de la luz en cuerpos en movimiento. ^[1] La aberración es distinta de la paralaje , que es un cambio en la posición aparente de un objeto relativamente cercano, medida por un observador en movimiento, en relación con objetos más distantes que definen un marco de referencia. La cantidad de paralaje depende de la distancia del objeto al observador, mientras que la aberración no. La aberración también está relacionada con la corrección del tiempo de luz y la emisión relativista , aunque a menudo se considera por separado de estos efectos.

La aberración es históricamente significativa debido a su papel en el desarrollo de las teorías de la luz , el electromagnetismo y, en última instancia, la teoría de la relatividad especial . Fue observada por primera vez a fines del siglo XVII por astrónomos que buscaban la paralaje estelar para confirmar el modelo heliocéntrico del Sistema Solar. Sin embargo, en ese momento no se entendió que fuera un fenómeno diferente. ^[2] En 1727, James Bradley proporcionó una explicación clásica para ella en términos de la velocidad finita de la luz en relación con el movimiento de la Tierra en su órbita alrededor del Sol, ^{[3] [4]} que utilizó para hacer una de las primeras mediciones de la velocidad de la luz. Sin embargo, la teoría de Bradley era incompatible con las teorías de la luz del siglo XIX, y la aberración se convirtió en una motivación importante para las teorías de arrastre del éter de Augustin Fresnel (en 1818) y GG Stokes (en 1845), y para la teoría del éter del electromagnetismo de Hendrik Lorentz en 1892. La aberración de la luz, junto con la elaboración de Lorentz de la electrodinámica de Maxwell , el problema del imán y el conductor en movimiento , los experimentos de deriva negativa del éter , así como el experimento de Fizeau , llevaron a Albert Einstein a desarrollar la teoría de la relatividad especial en 1905, que presenta una forma general de la ecuación para la aberración en términos de dicha teoría. ^[5]

Explicación

Rayos de luz que inciden sobre la Tierra en el sistema de referencia en reposo del Sol comparados con los mismos rayos en el sistema de referencia en reposo de la Tierra según la relatividad especial. El efecto se ha exagerado con fines ilustrativos.

La aberración puede explicarse como la diferencia de ángulo de un haz de luz en diferentes marcos de referencia inerciales . Una analogía común es considerar la dirección aparente de la lluvia que cae. Si la lluvia cae verticalmente en el marco de referencia de una persona que está parada, entonces para una persona que se mueve hacia adelante la lluvia parecerá llegar en un ángulo, lo que requiere que el observador en movimiento incline su paraguas hacia adelante. Cuanto más rápido se mueva el observador, más inclinación se necesitará.

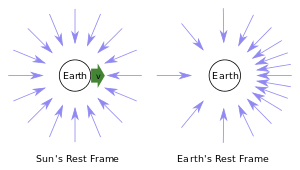
El efecto neto es que los rayos de luz que inciden sobre el observador en movimiento desde los lados en un marco estacionario llegarán en ángulo desde delante en el marco del observador en movimiento. Este efecto a veces se denomina efecto de "reflector" o "faro".

En el caso de la aberración anual de la luz estelar, la dirección de la luz estelar entrante, tal como se ve en el marco móvil de la Tierra, está inclinada con respecto al ángulo observado en el marco del Sol. Dado que la dirección del movimiento de la Tierra cambia durante su órbita, la dirección de esta inclinación cambia durante el transcurso del año y hace que la posición aparente de la estrella difiera de su posición real, medida en el marco inercial del Sol.

Aunque el razonamiento clásico proporciona una intuición sobre la aberración, conduce a una serie de paradojas físicas observables incluso en el nivel clásico (véase la historia). Se requiere la teoría de la relatividad especial para explicar correctamente la aberración. Sin embargo, la explicación relativista es muy similar a la clásica y en ambas teorías la aberración puede entenderse como un caso de adición de velocidades .

Explicación clásica

En el marco de referencia del Sol, considere un haz de luz con una velocidad igual a la velocidad de la luz , con componentes de velocidad x e y y , y por lo tanto con un ángulo tal que . Si la Tierra se mueve a una velocidad en la dirección x con respecto al Sol, entonces, por adición de velocidades, el componente x de la velocidad del haz en el marco de referencia de la Tierra es , y la velocidad y no cambia, . Por lo tanto, el ángulo de la luz en el marco de referencia de la Tierra en términos del ángulo en el marco del Sol es ${\displaystyle c}$ ${\displaystyle u_{x}}$ ${\displaystyle u_{y}}$ ${\displaystyle \theta }$ ${\displaystyle \tan(\theta )=u_{y}/u_{x}}$ ${\displaystyle v}$ ${\displaystyle u_{x}'=u_{x}+v}$ ${\displaystyle u_{y}'=u_{y}}$

${\displaystyle \tan(\phi )={\frac {u_{y}'}{u_{x}'}}={\frac {u_{y}}{u_{x}+v}}={\frac {\sin(\theta )}{v/c+\cos(\theta )}}}$

En el caso de , este resultado se reduce a , que en el límite puede aproximarse por . ${\displaystyle \theta =90^{\circ }}$ ${\displaystyle \tan(\theta -\phi )=v/c}$ ${\displaystyle v/c\ll 1}$ ${\displaystyle \theta -\phi =v/c}$

Explicación relativista

El razonamiento en el caso relativista es el mismo, excepto que se deben utilizar las fórmulas relativistas de adición de velocidades , que pueden derivarse de las transformaciones de Lorentz entre diferentes marcos de referencia. Estas fórmulas son

${\displaystyle u_{x}'=(u_{x}+v)/(1+u_{x}v/c^{2})}$

${\displaystyle u_{y}'=u_{y}/\gamma (1+u_{x}v/c^{2})}$

donde , dando los componentes del haz de luz en el marco de la Tierra en términos de los componentes en el marco del Sol. El ángulo del haz en el marco de la Tierra es, por tanto, ^[6] ${\displaystyle \gamma =1/{\sqrt {1-v^{2}/c^{2}}}}$

${\displaystyle \tan(\phi )={\frac {u_{y}'}{u_{x}'}}={\frac {u_{y}}{\gamma (u_{x}+v)}}={\frac {\sin(\theta )}{\gamma (v/c+\cos(\theta ))}}}$

En el caso de , este resultado se reduce a , y en el límite esto puede aproximarse por . Esta derivación relativista mantiene la velocidad de la luz constante en todos los marcos de referencia, a diferencia de la derivación clásica anterior. ${\displaystyle \theta =90^{\circ }}$ ${\displaystyle \sin(\theta -\phi )=v/c}$ ${\displaystyle v/c\ll 1}$ ${\displaystyle \theta -\phi =v/c}$ ${\displaystyle {\sqrt {u_{x}^{2}+u_{y}^{2}}}=c}$

Relación con la corrección del tiempo de luz y la transmisión relativista

La aberración, la corrección del tiempo de luz y la emisión relativista pueden considerarse el mismo fenómeno dependiendo del marco de referencia.

La aberración está relacionada con otros dos fenómenos, la corrección del tiempo de luz , que se debe al movimiento de un objeto observado durante el tiempo que tarda su luz en llegar a un observador, y la emisión relativista , que es una inclinación de la luz emitida por una fuente de luz en movimiento. Puede considerarse equivalente a ellos, pero en un marco de referencia inercial diferente. En la aberración, se considera que el observador se mueve en relación con una fuente de luz estacionaria (para simplificar ^[7] ), mientras que en la corrección del tiempo de luz y la emisión relativista se considera que la fuente de luz se mueve en relación con un observador estacionario.

Consideremos el caso de un observador y una fuente de luz que se mueven uno con respecto al otro a velocidad constante, con un haz de luz que se mueve desde la fuente hasta el observador. En el momento de la emisión, el haz en el sistema de referencia en reposo del observador está inclinado en comparación con el que está en el sistema de referencia en reposo de la fuente, como se entiende a través de la emisión relativista. Durante el tiempo que tarda el haz de luz en llegar al observador, la fuente de luz se mueve en el sistema de referencia del observador, y la "posición verdadera" de la fuente de luz se desplaza en relación con la posición aparente que ve el observador, como se explica por la corrección del tiempo de luz. Finalmente, el haz en el sistema de referencia del observador en el momento de la observación está inclinado en comparación con el haz en el sistema de referencia de la fuente, lo que puede entenderse como un efecto aberrativo. Por lo tanto, una persona en el sistema de referencia de la fuente de luz describiría la inclinación aparente del haz en términos de aberración, mientras que una persona en el sistema de referencia del observador lo describiría como un efecto del tiempo de luz.

La relación entre estos fenómenos sólo es válida si los sistemas de referencia del observador y de la fuente son sistemas inerciales. En la práctica, debido a que la Tierra no es un sistema de referencia en reposo inercial sino que experimenta una aceleración centrípeta hacia el Sol, muchos efectos aberrativo, como la aberración anual en la Tierra, no pueden considerarse correcciones del tiempo luz. Sin embargo, si el tiempo entre la emisión y la detección de la luz es corto en comparación con el período orbital de la Tierra, la Tierra puede considerarse aproximadamente como un sistema inercial y los efectos aberrativo son equivalentes a las correcciones del tiempo luz.

Tipos

El Almanaque Astronómico describe varios tipos diferentes de aberración, que surgen de diferentes componentes del movimiento de la Tierra y del objeto observado:

• Aberración estelar: "El desplazamiento angular aparente de la posición observada de un cuerpo celeste resultante del movimiento del observador. La aberración estelar se divide en componentes diurnos, anuales y seculares".
  • Aberración anual: "El componente de la aberración estelar resultante del movimiento de la Tierra alrededor del Sol".
  • Aberración diurna: "El componente de la aberración estelar resultante del movimiento diurno del observador alrededor del centro de la Tierra debido a la rotación de la Tierra".
  • Aberración secular: "Componente de la aberración estelar resultante del movimiento esencialmente uniforme y casi rectilíneo de todo el sistema solar en el espacio. La aberración secular suele ignorarse".
• Aberración planetaria: “El desplazamiento angular aparente de la posición observada de un cuerpo del sistema solar con respecto a su dirección geocéntrica instantánea, tal como la vería un observador en el geocentro. Este desplazamiento es causado por la aberración de la luz y el desplazamiento luz-tiempo ”. ^[8]

Aberración anual

Las estrellas situadas en los polos de la eclíptica parecen moverse en círculos, las estrellas situadas exactamente en el plano de la eclíptica se mueven en líneas y las estrellas situadas en ángulos intermedios se mueven en elipses. Aquí se muestran los movimientos aparentes de las estrellas con las latitudes eclípticas correspondientes a estos casos y con una longitud eclíptica de 270°.

La dirección de aberración de una estrella en el polo eclíptico norte difiere en diferentes épocas del año.

La aberración anual es causada por el movimiento de un observador en la Tierra a medida que el planeta gira alrededor del Sol . Debido a la excentricidad orbital , la velocidad orbital de la Tierra (en el marco de reposo del Sol) varía periódicamente durante el año a medida que el planeta recorre su órbita elíptica y, en consecuencia, la aberración también varía periódicamente, lo que generalmente hace que las estrellas parezcan moverse en pequeñas elipses . ${\displaystyle v}$

Aproximando la órbita de la Tierra como circular, el desplazamiento máximo de una estrella debido a la aberración anual se conoce como la constante de aberración , representada convencionalmente por . Puede calcularse utilizando la relación que sustituye la velocidad media de la Tierra en el marco del Sol por y la velocidad de la luz . Su valor aceptado es 20,49552  segundos de arco (seg) o 0,000099365  radianes (rad) (en J2000 ). ^[9] ${\displaystyle \kappa }$ ${\displaystyle \kappa =\theta -\phi \approx v/c}$ ${\displaystyle v}$ ${\displaystyle c}$

Suponiendo una órbita circular , la aberración anual hace que las estrellas exactamente en la eclíptica (el plano de la órbita de la Tierra) parezcan moverse hacia adelante y hacia atrás a lo largo de una línea recta, variando a cada lado de su posición en el marco del Sol. Una estrella que está precisamente en uno de los polos eclípticos (a 90° del plano eclíptico) parecerá moverse en un círculo de radio alrededor de su posición real, y las estrellas en latitudes eclípticas intermedias parecerán moverse a lo largo de una pequeña elipse . ${\displaystyle \kappa }$ ${\displaystyle \kappa }$

A modo de ejemplo, supongamos que un observador situado en un punto del círculo polar ártico ve una estrella en el polo norte de la eclíptica . Dicho observador verá el tránsito de la estrella por el cenit una vez al día (en sentido estricto, día sideral ). En el equinoccio de marzo , la órbita de la Tierra lleva al observador en dirección sur y, por lo tanto, la declinación aparente de la estrella se desplaza hacia el sur en un ángulo de . En el equinoccio de septiembre , la posición de la estrella se desplaza hacia el norte en una cantidad igual y opuesta. En cada solsticio , el desplazamiento en declinación es 0. Por el contrario, la cantidad de desplazamiento en ascensión recta es 0 en cada equinoccio y máxima en cada solsticio. ${\displaystyle \kappa }$

En realidad, la órbita de la Tierra es ligeramente elíptica en lugar de circular, y su velocidad varía un poco a lo largo de su trayectoria, lo que significa que la descripción anterior es solo aproximada. La aberración se calcula con mayor precisión utilizando la velocidad instantánea de la Tierra en relación con el baricentro del Sistema Solar. ^[9]

Obsérvese que el desplazamiento debido a la aberración es ortogonal a cualquier desplazamiento debido a la paralaje . Si la paralaje es detectable, el desplazamiento máximo hacia el sur ocurriría en diciembre y el desplazamiento máximo hacia el norte en junio. Es este movimiento aparentemente anómalo lo que tanto desconcertó a los primeros astrónomos.

Aberración solar anual

Un caso especial de aberración anual es la desviación casi constante del Sol respecto de su posición en el sistema de referencia en reposo hacia el oeste (visto desde la Tierra), en sentido opuesto al movimiento aparente del Sol a lo largo de la eclíptica (que es de oeste a este, visto desde la Tierra). La desviación hace que el Sol parezca estar retrasado (o retrasado) respecto de su posición en el sistema de referencia en reposo en la eclíptica en una posición o ángulo . ${\displaystyle \kappa }$ ${\displaystyle \kappa }$

Esta desviación puede describirse de manera equivalente como un efecto del tiempo de luz debido al movimiento de la Tierra durante los 8,3 minutos que tarda la luz en viajar desde el Sol hasta la Tierra. La relación es: [0,000099365 rad / 2 π rad] x [365,25 dx 24 h/dx 60 min/h] = 8,3167 min ≈ 8 min 19 s = 499 s. Esto es posible ya que el tiempo de tránsito de la luz solar es corto en relación con el período orbital de la Tierra, por lo que el marco de la Tierra puede aproximarse como inercial. En el marco de la Tierra, el Sol se mueve, a una velocidad media v = 29,789 km/s, una distancia de ≈ 14.864,7 km en el tiempo que tarda la luz en llegar a la Tierra, ≈ 499 s para la órbita de radio medio = 1 UA = 149.597.870,7 km. Esto da una corrección angular ≈ 0,000099364 rad = 20,49539 s, que puede resolverse para dar ≈ 0,000099365 rad = 20,49559 s, casi igual que la corrección aberracional (aquí está en radianes y no en segundos de arco). ${\displaystyle \kappa }$ ${\displaystyle \Delta x=vt}$ ${\displaystyle t=R/c}$ ${\displaystyle R}$ ${\displaystyle \tan(\theta )\approx \theta =\Delta x/R}$ ${\displaystyle \theta =v/c=\kappa }$ ${\displaystyle \kappa }$

Aberración diurna

La aberración diurna es causada por la velocidad del observador sobre la superficie de la Tierra en rotación . Por lo tanto, no solo depende del momento de la observación, sino también de la latitud y la longitud del observador. Su efecto es mucho menor que el de la aberración anual y es de solo 0,32 segundos de arco en el caso de un observador en el Ecuador , donde la velocidad de rotación es máxima. ^[10]

Aberración secular

El componente secular de la aberración, causado por el movimiento del Sistema Solar en el espacio, se ha subdividido en varios componentes: aberración resultante del movimiento del baricentro del sistema solar alrededor del centro de nuestra Galaxia , aberración resultante del movimiento de la Galaxia en relación con el Grupo Local y aberración resultante del movimiento del Grupo Local en relación con el fondo cósmico de microondas . ^{[11] : 6} La aberración secular afecta las posiciones aparentes de las estrellas y los objetos extragalácticos . La gran parte constante de la aberración secular no se puede observar directamente y "ha sido una práctica estándar absorber este gran efecto casi constante en las posiciones informadas" ^{[12] : 1} de las estrellas. ^[13]

En unos 200 millones de años, el Sol gira alrededor del centro galáctico, cuya ubicación medida está cerca de la ascensión recta (α = 266,4°) y la declinación (δ = −29,0°). ^{[12] : 2} El efecto constante, no observable, del movimiento del sistema solar alrededor del centro galáctico se ha calculado de diversas formas como 150 ^{[14] : 743} o 165 ^{[12] : 1} segundos de arco. La otra parte, observable, es una aceleración hacia el centro galáctico de aproximadamente 2,5 × 10 ⁻¹⁰  m/s ² , lo que produce un cambio de aberración de unos 5 μas/año. ^[15] Las mediciones de alta precisión que se extienden durante varios años pueden observar este cambio en la aberración secular, a menudo llamada deriva de aberración secular o aceleración del Sistema Solar, como un pequeño movimiento propio aparente . ^{[16] : 1  [12] : 1}

Recientemente, la astrometría de alta precisión de objetos extragalácticos utilizando tanto la Interferometría de Línea de Base Muy Larga como el observatorio espacial Gaia han medido con éxito este pequeño efecto. ^[16] La primera medición VLBI del movimiento aparente, durante un período de 20 años, de 555 objetos extragalácticos hacia el centro de nuestra galaxia en coordenadas ecuatoriales de α = 263° y δ = −20° indicó una deriva de aberración secular de 6,4 ±1,5 μas/año. ^{[16] : 1} Determinaciones posteriores utilizando una serie de mediciones VLBI que se extendieron durante casi 40 años determinaron que la deriva de aberración secular era de 5,83 ± 0,23 μas/año en la dirección α = 270,2 ± 2,3° y δ = −20,2° ± 3,6°. ^{[11] : 7} Las observaciones ópticas utilizando sólo 33 meses de datos del satélite Gaia de 1,6 millones de fuentes extragalácticas indicaron una aceleración del sistema solar de 2,32 ± 0,16 × 10 ⁻¹⁰  m/s ² y una deriva de aberración secular correspondiente de 5,05 ± 0,35 μas/año en la dirección de α = 269,1° ± 5,4°, δ = −31,6° ± 4,1°. Se espera que posteriores publicaciones de datos de Gaia , que incorporen alrededor de 66 y 120 meses de datos, reduzcan los errores aleatorios de estos resultados en factores de 0,35 y 0,15. ^{[17] [18] : 1,14} La última edición del Marco de Referencia Celeste Internacional (ICRF3) adoptó una constante de aberración galactocéntrica recomendada de 5,8 μas/año ^{[12] : 5,7} y recomendó una corrección para la aberración secular para obtener la mayor precisión posicional para tiempos distintos de la época de referencia 2015.0. ^{[11] : 17–19}

Aberración planetaria

La aberración planetaria es la combinación de la aberración de la luz (debida a la velocidad de la Tierra) y la corrección del tiempo de luz (debida al movimiento y la distancia del objeto), calculada en el marco de referencia en reposo del Sistema Solar. Ambas se determinan en el instante en que la luz del objeto en movimiento llega al observador en movimiento en la Tierra. Se denomina así porque se aplica generalmente a los planetas y otros objetos del Sistema Solar cuyo movimiento y distancia se conocen con precisión.

Descubrimiento y primeras observaciones

El descubrimiento de la aberración de la luz fue totalmente inesperado, y sólo gracias a una considerable perseverancia y perspicacia Bradley pudo explicarlo en 1727. Se originó a partir de los intentos de descubrir si las estrellas poseían paralajes apreciables .

Búsqueda de paralaje estelar

La teoría heliocéntrica copernicana del sistema solar había recibido confirmación por las observaciones de Galileo y Tycho Brahe y las investigaciones matemáticas de Kepler y Newton . ^[19] Ya en 1573, Thomas Digges había sugerido que el desplazamiento paraláctico de las estrellas debería ocurrir según el modelo heliocéntrico y, en consecuencia, si se pudiera observar la paralaje estelar, ayudaría a confirmar esta teoría. Muchos observadores afirmaron haber determinado tales paralajes, pero Tycho Brahe y Giovanni Battista Riccioli concluyeron que existían solo en las mentes de los observadores y se debían a errores instrumentales y personales. Sin embargo, en 1680 Jean Picard , en su Voyage d' Uranibourg , afirmó, como resultado de diez años de observaciones, que Polaris , la estrella polar, exhibía variaciones en su posición que ascendían a 40″ anuales. Algunos astrónomos intentaron explicar esto por paralaje, pero estos intentos fracasaron porque el movimiento difería del que produciría el paralaje. John Flamsteed , a partir de mediciones realizadas en 1689 y años posteriores con su cuadrante mural, concluyó de manera similar que la declinación de Polaris era 40″ menor en julio que en septiembre. Robert Hooke , en 1674, publicó sus observaciones de γ Draconis , una estrella de magnitud 2 ^m que pasa prácticamente por encima en la latitud de Londres (por lo tanto, sus observaciones están en gran parte libres de las complejas correcciones debidas a la refracción atmosférica ), y concluyó que esta estrella estaba 23″ más al norte en julio que en octubre. ^[19]

Observaciones de James Bradley

Observaciones de Bradley de γ Draconis y 35 Camelopardalis reducidas por Busch al año 1730.

Por consiguiente, cuando Bradley y Samuel Molyneux entraron en esta esfera de investigación en 1725, todavía había una considerable incertidumbre sobre si se habían observado o no paralajes estelares, y fue con la intención de responder definitivamente a esta pregunta que erigieron un gran telescopio en la casa de Molyneux en Kew . ^[4] Decidieron volver a investigar el movimiento de γ Draconis con un telescopio construido por George Graham (1675-1751), un célebre fabricante de instrumentos. Éste se fijó a una chimenea vertical de tal manera que permitiera una pequeña oscilación del ocular, cuya cantidad (es decir, la desviación de la vertical) se regulaba y medía mediante la introducción de un tornillo y una plomada. ^[19]

El instrumento se instaló en noviembre de 1725 y las observaciones de γ Draconis se realizaron a partir de diciembre. Se observó que la estrella se movía 40″ hacia el sur entre septiembre y marzo, y luego invirtió su curso de marzo a septiembre. ^[19] Al mismo tiempo, 35 Camelopardalis , una estrella con una ascensión recta casi exactamente opuesta a la de γ Draconis, estaba 19″ más al norte a principios de marzo que en septiembre. ^[20] La asimetría de estos resultados, que se esperaba que fueran imágenes especulares entre sí, fue completamente inesperada e inexplicable según las teorías existentes.

Hipótesis tempranas

Observación hipotética de γ Draconis si su movimiento fuera causado por paralaje.

Observación hipotética de γ Draconis y 35 Camelopardalis si sus movimientos fueran causados ​​por nutación.

Bradley y Molyneux discutieron varias hipótesis con la esperanza de encontrar la solución. Dado que el movimiento aparente evidentemente no era causado ni por paralaje ni por errores de observación, Bradley primero planteó la hipótesis de que podría deberse a oscilaciones en la orientación del eje de la Tierra en relación con la esfera celeste, un fenómeno conocido como nutación . 35 Se vio que Camelopardalis poseía un movimiento aparente que podría ser consistente con la nutación, pero dado que su declinación variaba solo la mitad que la de γ Draconis, era obvio que la nutación no proporcionaba la respuesta ^[21] (sin embargo, Bradley luego descubrió que la Tierra efectivamente nuta). ^[22] También investigó la posibilidad de que el movimiento se debiera a una distribución irregular de la atmósfera terrestre , lo que implicaba variaciones anormales en el índice de refracción, pero nuevamente obtuvo resultados negativos. ^[21]

El 19 de agosto de 1727, Bradley emprendió una nueva serie de observaciones utilizando un telescopio propio instalado en la rectoría de Wanstead . Este instrumento tenía la ventaja de un campo de visión más amplio y le permitió obtener posiciones precisas de un gran número de estrellas a lo largo de unos veinte años. Durante sus dos primeros años en Wanstead, estableció la existencia del fenómeno de la aberración más allá de toda duda, y esto también le permitió formular un conjunto de reglas que permitieran calcular el efecto sobre cualquier estrella dada en una fecha específica.

Desarrollo de la teoría de la aberración

Bradley finalmente desarrolló su explicación de la aberración alrededor de septiembre de 1728 y esta teoría fue presentada a la Royal Society a mediados de enero del año siguiente. Una historia bien conocida fue que vio el cambio de dirección de una veleta en un barco en el Támesis, causado no por una alteración del viento en sí, sino por un cambio de rumbo del barco en relación con la dirección del viento. ^[22] Sin embargo, no hay registro de este incidente en el propio relato de Bradley sobre el descubrimiento y, por lo tanto, puede ser apócrifo .

La siguiente tabla muestra la magnitud de la desviación de la declinación verdadera para γ Draconis y la dirección, en los planos del coluro solsticial y del meridiano principal eclíptico, de la tangente de la velocidad de la Tierra en su órbita para cada uno de los cuatro meses en los que se encuentran los extremos, así como la desviación esperada de la longitud eclíptica verdadera si Bradley hubiera medido su desviación de la ascensión recta:

Bradley propuso que la aberración de la luz no sólo afectaba a la declinación, sino también a la ascensión recta, de modo que una estrella en el polo de la eclíptica describiría una pequeña elipse con un diámetro de aproximadamente 40", pero para simplificar, supuso que se trataba de un círculo. Como sólo observó la desviación en declinación, y no en ascensión recta, sus cálculos para la desviación máxima de una estrella en el polo de la eclíptica son sólo para su declinación, que coincidirá con el diámetro del pequeño círculo descrito por dicha estrella. Para ocho estrellas diferentes, sus cálculos son los siguientes:

Basándose en estos cálculos, Bradley fue capaz de estimar la constante de aberración en 20,2", lo que equivale a 0,00009793 radianes, y con ello pudo estimar la velocidad de la luz en 183.300 millas (295.000 km) por segundo. ^[23] Al proyectar el pequeño círculo de una estrella en el polo de la eclíptica, pudo simplificar el cálculo de la relación entre la velocidad de la luz y la velocidad del movimiento anual de la Tierra en su órbita de la siguiente manera:

${\displaystyle \cos \left({\frac {1}{2}}\pi -0.00009793\right)=\sin(0.00009793)={\frac {v}{c}}}$

Así, la velocidad de la luz a la velocidad del movimiento anual de la Tierra en su órbita es 10,210 a uno, de donde se seguiría que la luz se mueve, o se propaga, tan lejos como del Sol a la Tierra en 8 minutos 12 segundos. ^[24]

La motivación original de la búsqueda de la paralaje estelar fue probar la teoría copernicana de que la Tierra gira alrededor del Sol. El cambio de aberración a lo largo del año demuestra el movimiento relativo de la Tierra y las estrellas.

Retrodicción sobre el argumento de la velocidad de la luz de Descartes

En el siglo anterior, René Descartes argumentó que si la luz no fuera instantánea, entonces las sombras de los objetos en movimiento se retrasarían; y si los tiempos de propagación sobre distancias terrestres fueran apreciables, entonces durante un eclipse lunar el Sol, la Tierra y la Luna estarían desalineados por horas de movimiento, contrariamente a la observación. Huygens comentó que, en los datos de velocidad de la luz de Rømer (que arrojan un tiempo de ida y vuelta Tierra-Luna de solo segundos), el ángulo de retraso sería imperceptible. Lo que ambos pasaron por alto ^[25] es que la aberración (como se entendió solo más tarde) contrarrestaría exactamente el retraso incluso si fuera grande, lo que dejaría a este método de eclipse completamente insensible a la velocidad de la luz. (De lo contrario, los métodos de retraso de sombra podrían detectar el movimiento de traslación absoluto, en contra de un principio básico de la relatividad ).

Teorías históricas de la aberración

El fenómeno de la aberración se convirtió en una fuerza impulsora de muchas teorías físicas durante los 200 años transcurridos entre su observación y la explicación de Albert Einstein.

La primera explicación clásica fue proporcionada en 1729, por James Bradley como se describió anteriormente, quien la atribuyó a la velocidad finita de la luz y al movimiento de la Tierra en su órbita alrededor del Sol . ^{[3] [4]} Sin embargo, esta explicación resultó inexacta una vez que se entendió mejor la naturaleza ondulatoria de la luz, y corregirla se convirtió en un objetivo principal de las teorías del éter luminífero del siglo XIX . Augustin-Jean Fresnel propuso una corrección debido al movimiento de un medio (el éter) a través del cual se propaga la luz, conocido como "arrastre parcial del éter" . Propuso que los objetos arrastran parcialmente el éter junto con ellos a medida que se mueven, y esta se convirtió en la explicación aceptada para la aberración durante algún tiempo. George Stokes propuso una teoría similar, explicando que la aberración ocurre debido al flujo de éter inducido por el movimiento de la Tierra. La evidencia acumulada en contra de estas explicaciones, combinada con una nueva comprensión de la naturaleza electromagnética de la luz, llevó a Hendrik Lorentz a desarrollar una teoría del electrón que presentaba un éter inmóvil y explicó que los objetos se contraen en longitud a medida que se mueven a través del éter. Motivado por estas teorías anteriores, Albert Einstein desarrolló la teoría de la relatividad especial en 1905, que proporciona la explicación moderna de la aberración.

La explicación clásica de Bradley

Figura 2: A medida que la luz se propaga por el telescopio, este se mueve, lo que requiere una inclinación del telescopio que depende de la velocidad de la luz. El ángulo aparente de la estrella φ difiere de su ángulo verdadero θ .

Bradley concibió una explicación en términos de una teoría corpuscular de la luz en la que la luz está hecha de partículas. ^[1] Su explicación clásica apela al movimiento de la Tierra en relación con un haz de partículas de luz que se mueven a una velocidad finita, y se desarrolla en el marco de referencia del Sol, a diferencia de la derivación clásica dada anteriormente.

Consideremos el caso en el que una estrella distante está inmóvil con respecto al Sol y está extremadamente lejos, por lo que se puede ignorar la paralaje. En el marco de reposo del Sol, esto significa que la luz de la estrella viaja en trayectorias paralelas al observador terrestre y llega en el mismo ángulo independientemente de dónde se encuentre la Tierra en su órbita. Supongamos que la estrella se observa en la Tierra con un telescopio, idealizado como un tubo estrecho. La luz entra en el tubo desde la estrella en un ángulo y viaja a una velocidad que le lleva un tiempo llegar al fondo del tubo, donde se detecta. Supongamos que las observaciones se realizan desde la Tierra, que se mueve a una velocidad . Durante el tránsito de la luz, el tubo se mueve una distancia . En consecuencia, para que las partículas de luz lleguen al fondo del tubo, el tubo debe estar inclinado en un ángulo diferente de , lo que da como resultado una posición aparente de la estrella en un ángulo . A medida que la Tierra avanza en su órbita, cambia de dirección, por lo que cambia con la época del año en que se realiza la observación. El ángulo aparente y el ángulo verdadero se relacionan mediante trigonometría como: ${\displaystyle \theta }$ ${\displaystyle c}$ ${\displaystyle h/c}$ ${\displaystyle v}$ ${\displaystyle vh/c}$ ${\displaystyle \phi }$ ${\displaystyle \theta }$ ${\displaystyle \phi }$ ${\displaystyle \phi }$

${\displaystyle \tan(\phi )={\frac {h\sin(\theta )}{hv/c+h\cos(\theta )}}={\frac {\sin(\theta )}{v/c+\cos(\theta )}}}$.

En el caso de , esto da . Si bien esto es diferente del resultado relativista más preciso descrito anteriormente, en el límite de ángulo pequeño y baja velocidad son aproximadamente iguales, dentro del error de las mediciones de la época de Bradley. Estos resultados le permitieron a Bradley realizar una de las primeras mediciones de la velocidad de la luz . ^{[24] [26]} ${\displaystyle \theta =90^{\circ }}$ ${\displaystyle \tan(\theta -\phi )=v/c}$

Éter luminífero

Young razonó que la aberración solo podría explicarse si el éter estuviera inmóvil en el marco del Sol. A la izquierda, la aberración estelar ocurre si se supone que el éter está inmóvil, lo que demuestra que el telescopio debe estar inclinado. A la derecha, la aberración desaparece si el éter se mueve con el telescopio y este no necesita estar inclinado.

A principios del siglo XIX se redescubrió la teoría ondulatoria de la luz y en 1804 Thomas Young adaptó la explicación de Bradley sobre la luz corpuscular a la luz ondulatoria que viaja a través de un medio conocido como éter luminífero. Su razonamiento era el mismo que el de Bradley, pero exigía que este medio estuviera inmóvil en el marco de referencia del Sol y pasara a través de la Tierra sin verse afectado, de lo contrario el medio (y por lo tanto la luz) se movería junto con la Tierra y no se observaría ninguna aberración. ^[27] Escribió:

Al considerar los fenómenos de la aberración de las estrellas, me inclino a creer que el éter luminífero impregna la sustancia de todos los cuerpos materiales con poca o ninguna resistencia, tan libremente tal vez como el viento pasa a través de un bosquecillo de árboles.

—Thomas  Young, 1804 ^[1]

Sin embargo, pronto quedó claro que la teoría de Young no podía explicar la aberración cuando había materiales con un índice de refracción distinto del del vacío . Un ejemplo importante es el de un telescopio lleno de agua. La velocidad de la luz en un telescopio de este tipo será menor que en el vacío, y viene dada por en lugar de donde es el índice de refracción del agua. Por lo tanto, según el razonamiento de Bradley y Young, el ángulo de aberración viene dado por ${\displaystyle c/n}$ ${\displaystyle c}$ ${\displaystyle n}$

${\displaystyle \tan(\phi )={\frac {\sin(\theta )}{v/(c/n)+\cos(\theta )}}}$.

que predice un ángulo de aberración dependiente del medio. Cuando se tiene en cuenta la refracción en el objetivo del telescopio, este resultado se desvía aún más del resultado del vacío. En 1810, François Arago realizó un experimento similar y descubrió que la aberración no se veía afectada por el medio en el telescopio, lo que proporcionó evidencia sólida contra la teoría de Young. Este experimento fue verificado posteriormente por muchos otros en las décadas siguientes, con mayor precisión por Airy en 1871, con el mismo resultado. ^[27]

Modelos de arrastre de éter

Arrastre del éter de Fresnel

En 1818, Augustin Fresnel desarrolló una explicación modificada para explicar el telescopio de agua y otros fenómenos de aberración. Explicó que el éter está generalmente en reposo en el marco de referencia del Sol, pero los objetos arrastran parcialmente el éter junto con ellos a medida que se mueven. Es decir, el éter en un objeto de índice de refracción que se mueve a velocidad es parcialmente arrastrado por una velocidad que lleva consigo la luz. Este factor se conoce como "coeficiente de arrastre de Fresnel". Este efecto de arrastre, junto con la refracción en el objetivo del telescopio, compensa la velocidad más lenta de la luz en el telescopio de agua en la explicación de Bradley. ^[a] Con esta modificación, Fresnel obtuvo el resultado de vacío de Bradley incluso para telescopios que no eran de vacío, y también pudo predecir muchos otros fenómenos relacionados con la propagación de la luz en cuerpos en movimiento. El coeficiente de arrastre de Fresnel se convirtió en la explicación dominante de la aberración durante las siguientes décadas. ${\displaystyle n}$ ${\displaystyle v}$ ${\displaystyle (1-1/n^{2})v}$

Ilustración conceptual de la teoría de Stokes sobre el arrastre del éter. En el marco de referencia en reposo del Sol, la Tierra se mueve hacia la derecha a través del éter, en el que induce una corriente local. Un rayo de luz (en rojo) que proviene de la vertical se ve arrastrado e inclinado debido al flujo del éter.

El arrastre de éter de Stokes

Sin embargo, el hecho de que la luz esté polarizada (descubierto por el propio Fresnel) llevó a científicos como Cauchy y Green a creer que el éter era un sólido elástico totalmente inmóvil, a diferencia del éter fluido de Fresnel. Por lo tanto, surgió una renovada necesidad de una explicación de la aberración que fuera coherente tanto con las predicciones de Fresnel (y las observaciones de Arago) como con la polarización.

En 1845, Stokes propuso un éter "similar a la masilla" que actúa como un líquido en grandes escalas pero como un sólido en pequeñas escalas, lo que admite tanto las vibraciones transversales requeridas para la luz polarizada como el flujo de éter necesario para explicar la aberración. Haciendo solo las suposiciones de que el fluido es irrotacional y que las condiciones límite del flujo son tales que el éter tiene velocidad cero lejos de la Tierra, pero se mueve a la velocidad de la Tierra en su superficie y dentro de ella, pudo explicar completamente la aberración. ^[b] La velocidad del éter fuera de la Tierra disminuiría en función de la distancia a la Tierra, por lo que los rayos de luz de las estrellas serían arrastrados progresivamente a medida que se acercaran a la superficie de la Tierra. El movimiento de la Tierra no se vería afectado por el éter debido a la paradoja de D'Alembert .

Las teorías de Fresnel y Stokes fueron populares. Sin embargo, la cuestión de la aberración se dejó de lado durante gran parte de la segunda mitad del siglo XIX, cuando la investigación se centró en las propiedades electromagnéticas del éter.

Contracción de la longitud de Lorentz

En la década de 1880, una vez que se comprendió mejor el electromagnetismo, el interés volvió a centrarse en el problema de la aberración. Para entonces, se conocían los fallos de las teorías de Fresnel y Stokes. La teoría de Fresnel exigía que la velocidad relativa del éter y la materia fuera diferente para la luz de diferentes colores, y se demostró que las condiciones de contorno que Stokes había asumido en su teoría eran incompatibles con su suposición de flujo irrotacional. ^{[1] [27] [28]} Al mismo tiempo, las teorías modernas del éter electromagnético no podían explicar en absoluto la aberración. Muchos científicos, como Maxwell , Heaviside y Hertz, intentaron sin éxito resolver estos problemas incorporando las teorías de Fresnel o Stokes a las nuevas leyes electromagnéticas de Maxwell .

Hendrik Lorentz dedicó un esfuerzo considerable a este respecto. Después de trabajar en este problema durante una década, los problemas con la teoría de Stokes le hicieron abandonarla y seguir la sugerencia de Fresnel de un éter (en su mayor parte) estacionario (1892, 1895). Sin embargo, en el modelo de Lorentz el éter era completamente inmóvil, como los éteres electromagnéticos de Cauchy, Green y Maxwell y a diferencia del éter de Fresnel. Obtuvo el coeficiente de arrastre de Fresnel a partir de modificaciones de la teoría electromagnética de Maxwell, incluida una modificación de las coordenadas temporales en sistemas móviles ("tiempo local"). Para explicar el experimento de Michelson-Morley (1887), que aparentemente contradecía las teorías del éter inmóvil de Fresnel y de Lorentz, y aparentemente confirmaba el arrastre completo del éter de Stokes, Lorentz teorizó (1892) que los objetos experimentan una " contracción de longitud " por un factor de en la dirección de su movimiento a través del éter. De esta manera, la aberración (y todos los fenómenos ópticos relacionados) pueden explicarse en el contexto de un éter inmóvil. La teoría de Lorentz se convirtió en la base de muchas investigaciones en la década siguiente y más allá. Sus predicciones sobre la aberración son idénticas a las de la teoría relativista. ^{[27] [29]} ${\displaystyle {\sqrt {1-v^{2}/c^{2}}}}$

Relatividad especial

La teoría de Lorentz se ajustó bien a la experimentación, pero era complicada y hacía muchas suposiciones físicas sin fundamento sobre la naturaleza microscópica de los medios electromagnéticos. En su teoría de la relatividad especial de 1905, Albert Einstein reinterpretó los resultados de la teoría de Lorentz en un marco conceptual mucho más simple y natural que descartaba la idea de un éter. Su derivación se da arriba y ahora es la explicación aceptada. Robert S. Shankland informó sobre algunas conversaciones con Einstein, en las que Einstein enfatizó la importancia de la aberración: ^[30]

Agregó que los resultados experimentales que más lo habían influenciado fueron las observaciones de la aberración estelar y las mediciones de Fizeau sobre la velocidad de la luz en el agua en movimiento. "Fueron suficientes", dijo.

Otras motivaciones importantes para el desarrollo de la relatividad por parte de Einstein fueron el problema del imán móvil y el conductor e (indirectamente) los experimentos de deriva negativa del éter, ya mencionados por él en la introducción de su primer artículo sobre la relatividad. Einstein escribió en una nota en 1952: ^[5]

Mi propio pensamiento fue influenciado más indirectamente por el famoso experimento de Michelson-Morley. Lo conocí a través de la investigación pionera de Lorentz sobre la electrodinámica de los cuerpos en movimiento (1895), de la que sabía antes del establecimiento de la teoría especial de la relatividad. La hipótesis básica de Lorentz de un éter en reposo no me pareció directamente convincente, ya que condujo a una interpretación [tachado: para mí artificial] del experimento de Michelson-Morley, que [tachado: no me convenció] me pareció antinatural. Mi camino directo hacia la sp. th. rel. estuvo determinado principalmente por la convicción de que la fuerza electromotriz inducida en un conductor que se mueve en un campo magnético no es otra cosa que un campo eléctrico. Pero el resultado del experimento de Fizeau y el fenómeno de la aberración también me guiaron.

Aunque el resultado de Einstein es el mismo que la ecuación original de Bradley, excepto por un factor adicional de , el resultado de Bradley no solo da el límite clásico del caso relativista, en el sentido de que da predicciones incorrectas incluso a bajas velocidades relativas. La explicación de Bradley no puede dar cuenta de situaciones como el telescopio acuático, ni de muchos otros efectos ópticos (como la interferencia) que podrían ocurrir dentro del telescopio. Esto se debe a que en el marco de la Tierra predice que la dirección de propagación del haz de luz en el telescopio no es normal a los frentes de onda del haz, en contradicción con la teoría del electromagnetismo de Maxwell . Tampoco preserva la velocidad de la luz c entre marcos. Sin embargo, Bradley infirió correctamente que el efecto se debía a las velocidades relativas. ${\displaystyle \gamma }$

Véase también

• Lugar aparente
• Paralaje estelar
• Nutación astronómica
• Movimiento propio
• Cronología del electromagnetismo y la óptica clásica
• Aberración relativista

Notas

1. Más detalladamente, Fresnel explica que la luz entrante de ángulo primero se refracta en el extremo del telescopio, a un nuevo ángulo dentro del telescopio. Esto puede explicarse por la ley de Snell , dando . Luego debe tenerse en cuenta la resistencia. Sin resistencia, los componentes x e y de la luz en el telescopio son y , pero la resistencia modifica el componente x a si la Tierra se mueve con velocidad . Si es ángulo y es la velocidad de la luz con estos componentes de velocidad, entonces por el razonamiento de Bradley donde es la longitud de trayectoria modificada a través del agua y t es el tiempo que tarda la luz en recorrer la distancia h, . Al resolver estas ecuaciones para en términos de se obtiene el resultado de vacío de Bradley. ${\displaystyle \theta }$ ${\displaystyle \psi }$ ${\displaystyle \sin(\theta -\phi )=n\sin(\psi -\phi )}$ ${\displaystyle (c/n)\sin(\psi )}$ ${\displaystyle (c/n)\cos(\psi )}$ ${\displaystyle (c/n)\cos(\psi )-(1-1/n^{2})v}$ ${\displaystyle v}$ ${\displaystyle \alpha }$ ${\displaystyle v_{l}}$ ${\displaystyle \tan(\phi )={\frac {h\sin(\alpha )}{vt+h\cos(\alpha )}}}$ ${\displaystyle h}$ ${\displaystyle t=h/v_{l}}$ ${\displaystyle \phi }$ ${\displaystyle \theta }$

2. 

   El frente de onda que se propaga moviéndose a través del éter.

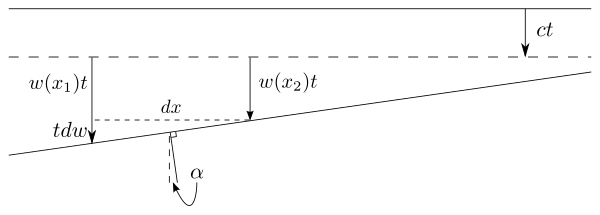
   La derivación de Stokes puede resumirse de la siguiente manera: considere un frente de onda que se mueve en la dirección z hacia abajo. Digamos que el éter tiene un campo de velocidad en función de . Ahora, el movimiento del éter en las direcciones x e y no afecta al frente de onda, pero el movimiento en la dirección z lo hace avanzar (además de la cantidad que avanza a la velocidad c). Si la velocidad z del éter varía en el espacio, por ejemplo, si es más lenta para x más altas como se muestra en la figura, entonces el frente de onda se vuelve angular, por un ángulo . Ahora, digamos que en el tiempo t el frente de onda se ha movido un lapso (suponiendo que la velocidad del éter es insignificante en comparación con la velocidad de la luz). Entonces, por cada distancia que desciende el rayo, se dobla un ángulo , y por lo tanto el ángulo total por el que ha cambiado después de viajar a través de todo el fluido es ${\displaystyle u,v,w}$ ${\displaystyle x,y,z}$ ${\displaystyle \tan(\alpha )=tdw/dx}$ ${\displaystyle dz\approx ct}$ ${\displaystyle dz}$ ${\displaystyle \alpha \approx (dw/dx)(dz/c)}$

   ${\displaystyle \alpha \approx {\frac {1}{c}}\int {\frac {\partial w}{\partial x}}dz}$

   Si el fluido es irrotacional satisfará las ecuaciones de Cauchy-Riemann , una de las cuales es

   ${\displaystyle {\frac {\partial w}{\partial x}}={\frac {\partial u}{\partial z}}}$.

   Insertando esto en el resultado anterior se obtiene un ángulo de aberración donde s representa el componente x de la velocidad del éter al principio y al final del rayo. Lejos de la Tierra, el éter tiene velocidad cero, por lo que y en la superficie de la Tierra tiene la velocidad de la Tierra . Por lo tanto, finalmente obtenemos ${\displaystyle \alpha =(u_{2}-u_{1})/c}$ ${\displaystyle u}$ ${\displaystyle u_{2}=0}$ ${\displaystyle v}$

   ${\displaystyle \alpha \approx {\frac {v}{c}}}$

   que es el resultado de aberración conocido.

Referencias

1. Schaffner, Kenneth F. (1972). Teorías del éter en el siglo XIX . Oxford: Pergamon Press. págs. 99-117 y 255-273. ISBN 0-08-015674-6.
2. Williams, MEW (1979). "La supuesta medición de Flamsteed del paralaje anual de la estrella polar". Revista de Historia de la Astronomía . 10 (2): 102–116. Bibcode :1979JHA....10..102W. doi :10.1177/002182867901000203. S2CID  118565124.
3. Bradley, James (1727–1728). "Una carta del reverendo Sr. James Bradley Savilian, profesor de astronomía en Oxford y FRS al Dr. Edmond Halley, astrónomo, reg., etc., dando cuenta de un nuevo descubrimiento del movimiento de las estrellas fijas". Phil. Trans. R. Soc . 35 (406): 637–661. Bibcode :1727RSPT...35..637B. doi : 10.1098/rstl.1727.0064 .
4. Hirschfeld, Alan (2001). Parallax: La carrera para medir el cosmos . Nueva York, Nueva York: Henry Holt. ISBN 0-8050-7133-4.
5. Norton, John D. (2004). "Investigaciones de Einstein sobre la electrodinámica covariante galileana antes de 1905". Archivo de Historia de las Ciencias Exactas . 59 (1): 45–105. Código Bibliográfico :2004AHES...59...45N. doi :10.1007/s00407-004-0085-6. S2CID  17459755. Archivado desde el original el 11 de enero de 2009.
6. Richard A. Mould (2001). Relatividad básica (2.ª ed.). Springer. pág. 8. ISBN 0-387-95210-1.
7. De hecho, la fuente de luz no necesita ser estacionaria; pensemos, por ejemplo, en estrellas binarias eclipsantes: giran a gran velocidad —y con vectores de velocidad siempre cambiantes y diferentes— una alrededor de la otra, pero aparecen como un solo punto todo el tiempo.
8. Oficina del Almanaque Náutico de los Estados Unidos (21 de marzo de 2014). "Glosario". Almanaque astronómico para el año 2015 y su complemento, The Astronomical Almanac Online. Washington, DC: Oficina de Imprenta del Gobierno de los Estados Unidos (publicado en 2014). pág. M1. ISBN 9780707741499.
9. Kovalevsky, Jean y Seidelmann, P. Kenneth (2004). Fundamentos de astrometría . Cambridge: Cambridge University Press . ISBN 0-521-64216-7.
10. Newcomb, Simon (1960). Un compendio de astronomía esférica . Macmillan, 1906 – republicado por Dover .
11. Charlot, P.; Jacobs, CS; Gordon, D.; Lambert, S.; et al. (2020). "La tercera realización del Marco de Referencia Celeste Internacional mediante interferometría de línea base muy larga". Astronomía y Astrofísica . 644 : A159. arXiv : 2010.13625 . Bibcode :2020A&A...644A.159C. doi :10.1051/0004-6361/202038368. S2CID  225068756.
12. MacMillan, DS; Fey, A.; Gipson, JM; et al. (2019). "Aceleración galactocéntrica en análisis VLBI". Astronomía y Astrofísica . 630 : A93. Bibcode :2019A&A...630A..93M. doi :10.1051/0004-6361/201935379. S2CID  198471325.
13. Hagihara, Yusuke (1933). "Sobre la teoría de la aberración secular". Actas de la Sociedad Físico-Matemática de Japón . 3.ª serie. 15 (3–6): 175. doi :10.11429/ppmsj1919.15.3-6_155. La corrección de las posiciones de las estrellas con aberración secular no es en absoluto necesaria e incluso resulta incómoda, siempre que el movimiento solar se mantenga uniforme y rectilíneo.
14. Kovalevsky, J. (2003). "Aberración en movimientos propios". Astronomía y Astrofísica . 404 (2): 743–747. Bibcode :2003A&A...404..743K. doi : 10.1051/0004-6361:20030560 .
15. Kopeikin, S.; Makarov, V. (2006). "Efectos astrométricos de la aberración secular". The Astronomical Journal (Estados Unidos) . 131 (3): 1471–1478. arXiv : astro-ph/0508505 . Código Bibliográfico :2006AJ....131.1471K. doi : 10.1086/500170 .
16. Titov, O.; Lambert, SB; Gontier, A.-M. (2011). "Medición VLBI de la deriva de la aberración secular". Astronomía y Astrofísica . 529 : A91. arXiv : 1009.3698 . Bibcode :2011A&A...529A..91T. doi :10.1051/0004-6361/201015718. S2CID  119305429.
17. "Medición de la aceleración del sistema solar con respecto al universo distante realizada por Gaia". esa.int . Agencia Espacial Europea . 3 de diciembre de 2020 . Consultado el 14 de septiembre de 2022 .
18. Colaboración Gaia; Klioner, SA; et al. (2021). "Lanzamiento de datos tempranos de Gaia 3: aceleración del sistema solar a partir de la astrometría de Gaia". Astronomía y astrofísica . 649 : A9. arXiv : 2012.02036 . Código Bibliográfico :2021A&A...649A...9G. doi :10.1051/0004-6361/202039734.
19. Eppenstein (1911), pág. 54.
20. Bradley, James; Rigaud, Stephen Peter (1832). Obras misceláneas y correspondencia del reverendo James Bradley, DD, FRS Oxford: University Press. pág. 11.
21. Eppenstein (1911), pág. 55.
22. Berry, Arthur (1961) [1898]. Una breve historia de la astronomía . Dover . ISBN 9780486202105.
23. Hoiberg, Dale H., ed. (2010). "aberración, constante de" . Encyclopædia Britannica . Vol. I: A-ak Bayes (15.ª ed.). Chicago, IL: Encyclopædia Britannica Inc., págs. 30. ISBN. 978-1-59339-837-8.
24. James Bradley (1729). "Un relato de un nuevo descubrimiento del movimiento de las estrellas fijas". Philosophical Transactions of the Royal Society . 35 : 637–661. doi : 10.1098/rstl.1727.0064 .
25. Sakellariadis, Spyros (1982). "La prueba experimental de Descartes de la velocidad infinita de la luz y la réplica de Huygens". Archivo de Historia de las Ciencias Exactas . 26 (1): 1–12. doi :10.1007/BF00348308. ISSN  0003-9519. JSTOR  41133639. S2CID  118187860.
26. Enciclopedia Británica Archivado el 11 de noviembre de 2013 en Wayback Machine.
27. Whittaker, Edmund Taylor (1910). Una historia de las teorías del éter y la electricidad (1. ed.). Dublín: Longman, Green and Co. Archivado desde el original el 15 de febrero de 2016.
    Whittaker, Edmund Taylor (1953). Una historia de las teorías del éter y la electricidad (2. ed.). T. Nelson.
28. Janssen, Michel y Stachel, John (2010). "La óptica y la electrodinámica de los cuerpos en movimiento" (PDF) . En John Stachel (ed.). Going Critical . Springer. ISBN 978-1-4020-1308-9. Archivado (PDF) del original el 9 de octubre de 2022.
29. Darrigol, Olivier (2000). Electrodinámica desde Ampére hasta Einstein . Oxford: Clarendon Press. ISBN 0-19-850594-9.
30. Shankland, RS (1963). "Conversaciones con Albert Einstein". Revista estadounidense de física . 31 (1): 47–57. Código Bibliográfico :1963AmJPh..31...47S. doi :10.1119/1.1969236.

•  Este artículo incorpora texto de una publicación que ahora es de dominio público :  Eppenstein, Otto (1911). "Aberración". Encyclopædia Britannica . Vol. 1 (11.ª ed.). págs. 54–61.

Lectura adicional

• P. Kenneth Seidelmann (Ed.), Suplemento explicativo del Almanaque astronómico (University Science Books, 1992), 127–135, 700.
• Stephen Peter Rigaud , Obras misceláneas y correspondencia del reverendo James Bradley, DDFRS (1832).
• Charles Hutton , Diccionario matemático y filosófico (1795).
• HH Turner, Descubrimiento astronómico (1904).
• Thomas Simpson , Ensayos sobre varios temas curiosos y útiles en matemáticas especulativas y mixtas (1740).
• de:August Ludwig Busch, Reducción de las observaciones realizadas por Bradley en Kew y Wanted para determinar las cantidades de aberración y nutación (1838).

Enlaces externos

• Courtney Seligman sobre las observaciones de Bradley