
La cuna de Newton es un dispositivo, generalmente hecho de metal, que demuestra los principios de conservación del momento y conservación de la energía en física con esferas oscilantes . Cuando una esfera en el extremo se levanta y se suelta, golpea las esferas estacionarias, comprimiéndolas y transmitiendo así una onda de presión a través de las esferas estacionarias, lo que crea una fuerza que empuja la última esfera hacia arriba. La última esfera se balancea hacia atrás y golpea las esferas estacionarias, repitiendo el efecto en la dirección opuesta. El dispositivo lleva el nombre del científico inglés del siglo XVII Sir Isaac Newton y fue diseñado por el científico francés Edme Mariotte . También se conoce como péndulo de Newton , bolas de Newton , balancín de Newton o clicker de bolas ejecutivo (ya que el dispositivo hace un clic cada vez que las bolas chocan, lo que hacen repetidamente en un ritmo constante ). [1] [2]
Cuando una de las bolas de los extremos ("la primera") se tira hacia un lado, la cuerda que la sujeta hace que siga un arco ascendente. Cuando se suelta la bola, golpea la segunda bola y se detiene casi por completo. La bola del lado opuesto adquiere la mayor parte de la velocidad de la primera bola y oscila en un arco casi tan alto como la altura de liberación de la primera bola. Esto demuestra que la última bola recibe la mayor parte de la energía y el impulso de la primera bola. El impacto produce una onda sónica que se propaga a través de las bolas intermedias. Cualquier material eficientemente elástico, como el acero, hace esto, siempre que la energía cinética se almacene temporalmente como energía potencial en la compresión del material en lugar de perderse como calor . Esto es similar a hacer rebotar una moneda de una fila de monedas en contacto golpeándola con otra moneda, y que sucede incluso si la primera moneda golpeada está restringida al presionar su centro de tal manera que no puede moverse. [ cita requerida ]
Todas las bolas se mueven ligeramente después del impacto inicial, pero la última bola recibe la mayor parte de la energía inicial del impacto de la primera. Cuando se dejan caer dos (o tres) bolas, las dos (o tres) bolas del lado opuesto se balancean hacia afuera. Algunos dicen que este comportamiento demuestra la conservación del momento y la energía cinética en las colisiones elásticas. Sin embargo, si las bolas que chocan se comportan como se describió anteriormente con la misma masa y la misma velocidad antes y después de las colisiones, entonces cualquier función de masa y velocidad se conserva en tal evento. [3] Por lo tanto, esta explicación de primer nivel es una descripción verdadera, pero no completa, del movimiento.

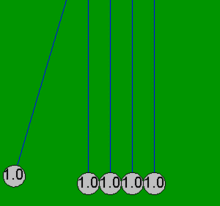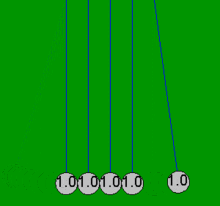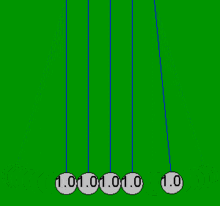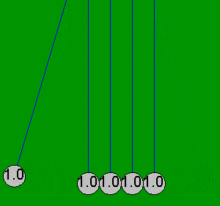
La cuna de Newton se puede modelar con bastante precisión con ecuaciones matemáticas simples, suponiendo que las bolas siempre chocan en pares. Si una bola golpea cuatro bolas estacionarias que ya están en contacto, estas ecuaciones simples no pueden explicar los movimientos resultantes en las cinco bolas, que no se deben a pérdidas por fricción . Por ejemplo, en una cuna de Newton real, la cuarta bola tiene algún movimiento y la primera tiene un ligero movimiento inverso. Todas las animaciones de este artículo muestran una acción idealizada (solución simple) que solo ocurre si las bolas no se tocan inicialmente y solo chocan en pares.
La conservación del momento (masa × velocidad) y la energía cinética ( 1 / 2 × masa × velocidad 2 ) se pueden utilizar para encontrar las velocidades resultantes para dos objetos perfectamente elásticos en colisión . Estas dos ecuaciones se utilizan para determinar las velocidades resultantes de los dos objetos. Para el caso de dos bolas limitadas a una trayectoria recta por las cuerdas en la cuna, las velocidades son un solo número en lugar de un vector 3D para el espacio 3D, por lo que las matemáticas requieren solo dos ecuaciones para resolver dos incógnitas. Cuando los dos objetos tienen la misma masa, la solución es simple: el objeto en movimiento se detiene en relación con el estacionario y el estacionario recoge toda la velocidad inicial del otro. Esto supone objetos perfectamente elásticos, por lo que no hay necesidad de tener en cuenta las pérdidas de energía térmica y sonora.
El acero no se comprime mucho, pero su elasticidad es muy eficiente, por lo que no genera mucho calor residual . El simple efecto de dos objetos de la misma masa que chocan de manera eficientemente elástica y que siguen una trayectoria recta es la base del efecto que se observa en la cuna y da una solución aproximada a todas sus actividades.
En el caso de una secuencia de objetos elásticos de la misma masa que siguen una trayectoria recta, el efecto continúa en cada objeto sucesivo. Por ejemplo, cuando se dejan caer dos pelotas para golpear tres pelotas estacionarias en una cuna, hay una distancia pequeña, inadvertida pero crucial, entre las dos pelotas que se dejan caer, y la acción es la siguiente: la primera pelota en movimiento que golpea a la primera pelota estacionaria (la segunda pelota que golpea a la tercera) transfiere todo su impulso a la tercera pelota y se detiene. La tercera pelota luego transfiere el impulso a la cuarta pelota y se detiene, y luego la cuarta a la quinta pelota.
Justo detrás de esta secuencia, la segunda bola en movimiento transfiere su impulso a la primera bola en movimiento que acaba de detenerse, y la secuencia se repite inmediatamente e imperceptiblemente detrás de la primera secuencia, expulsando la cuarta bola justo detrás de la quinta bola con la misma pequeña separación que había entre las dos bolas que chocaron inicialmente. Si simplemente se tocan cuando chocan con la tercera bola, la precisión requiere la solución más completa que se muestra a continuación.
El efecto de la última bola expulsada con una velocidad casi igual a la de la primera bola se puede ver al deslizar una moneda sobre una mesa en una línea de monedas idénticas, siempre que la moneda que golpea y sus objetivos gemelos estén en línea recta. El efecto se puede ver de manera similar en las bolas de billar. El efecto también se puede ver cuando una onda de presión aguda y fuerte golpea un material homogéneo denso inmerso en un medio menos denso . Si los átomos , moléculas o subvolúmenes de mayor escala idénticos del material homogéneo denso están al menos parcialmente conectados elásticamente entre sí por fuerzas electrostáticas, pueden actuar como una secuencia de bolas elásticas idénticas en colisión.
Los átomos, moléculas o subvolúmenes circundantes que experimentan la onda de presión actúan para restringirse entre sí de manera similar a cómo la cuerda restringe las bolas de la cuna a una línea recta. Como ejemplo médico, las ondas de choque de la litotricia se pueden enviar a través de la piel y el tejido sin causar daño a los cálculos renales que estallan . El lado de los cálculos opuesto a la onda de presión entrante estalla, no el lado que recibe el golpe inicial. En el juego indio carrom , un atacante se detiene después de golpear una pieza de juego estacionaria, transfiriendo todo su impulso a la pieza que fue golpeada.
Para que la solución simple prediga con precisión la acción, ninguna pareja en medio de una colisión puede tocar la tercera bola, porque la presencia de la tercera bola hace que la bola golpeada parezca más masiva. La aplicación de las dos ecuaciones de conservación para resolver las velocidades finales de tres o más bolas en una sola colisión da como resultado muchas soluciones posibles, por lo que estos dos principios no son suficientes para determinar la acción resultante.
Incluso cuando la separación inicial es pequeña, una tercera bola puede verse involucrada en la colisión si la separación inicial no es lo suficientemente grande. Cuando esto ocurre, se debe utilizar el método de solución completa que se describe a continuación.
Las bolas de acero pequeñas funcionan bien porque conservan su elasticidad de manera eficiente con poca pérdida de calor bajo golpes fuertes y no se comprimen mucho (hasta aproximadamente 30 μm en una pequeña cuna de Newton). Las compresiones pequeñas y rígidas significan que ocurren rápidamente, menos de 200 microsegundos, por lo que es más probable que las bolas de acero completen una colisión antes de tocar una tercera bola cercana. Las bolas elásticas más blandas requieren una mayor separación para maximizar el efecto de las colisiones por pares.
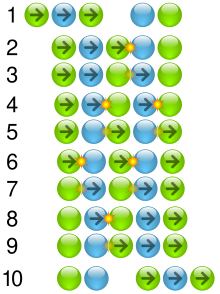
Una cuna que mejor se adapte a la solución simple debe tener una separación inicial entre las bolas que mida al menos el doble de la cantidad que se comprime cada bola, pero la mayoría no lo hace. Esta sección describe la acción cuando la separación inicial no es suficiente y en colisiones posteriores que involucran más de dos bolas incluso cuando hay una separación inicial. Esta solución se simplifica a la solución simple cuando solo dos bolas se tocan durante una colisión. Se aplica a todas las bolas idénticas perfectamente elásticas que no tienen pérdidas de energía debido a la fricción y se puede aproximar con materiales como acero, vidrio, plástico y caucho.
En el caso de dos bolas que chocan, solo se necesitan las dos ecuaciones de conservación del momento y la energía para resolver las dos velocidades desconocidas resultantes. En el caso de tres o más bolas elásticas que chocan simultáneamente, las compresibilidades relativas de las superficies en colisión son las variables adicionales que determinan el resultado. Por ejemplo, cinco bolas tienen cuatro puntos de colisión y al escalar (dividir) tres de ellas por la cuarta se obtienen las tres variables adicionales necesarias para resolver las cinco velocidades posteriores a la colisión.
La acción newtoniana, lagrangiana, hamiltoniana y estacionaria son las diferentes formas de expresar matemáticamente la mecánica clásica . Describen la misma física, pero deben resolverse con métodos diferentes. Todas imponen la conservación de la energía y el momento. La ley de Newton se ha utilizado en artículos de investigación. Se aplica a cada bola y la suma de fuerzas se hace igual a cero. Por lo tanto, hay cinco ecuaciones, una para cada bola, y cinco incógnitas, una para cada velocidad. Si las bolas son idénticas, la compresibilidad absoluta de las superficies se vuelve irrelevante, porque se puede dividir en ambos lados de las cinco ecuaciones, lo que produce cero.
La determinación de las velocidades [4] [5] [6] para el caso de una pelota que golpea cuatro pelotas que inicialmente se tocan se encuentra modelando las pelotas como pesos con resortes no tradicionales en sus superficies de colisión. La mayoría de los materiales, como el acero, que son eficientemente elásticos siguen aproximadamente la ley de fuerza de Hooke para resortes, , pero debido a que el área de contacto para una esfera aumenta a medida que aumenta la fuerza, las pelotas elásticas que chocan siguen el ajuste de Hertz a la ley de Hooke, . Esta y la ley de Newton para el movimiento ( ) se aplican a cada pelota, dando cinco ecuaciones diferenciales simples pero interdependientes que se pueden resolver numéricamente.
Cuando la quinta bola comienza a acelerar , recibe impulso y energía de la tercera y cuarta bolas a través de la acción elástica de sus superficies comprimidas. Para bolas elásticas idénticas de cualquier tipo con bolas que inicialmente se tocan, la acción es la misma para el primer golpe, excepto que el tiempo para completar una colisión aumenta en materiales más blandos. Entre el cuarenta y el cincuenta por ciento de la energía cinética de la bola inicial de un golpe de una sola bola se almacena en las superficies de la bola como energía potencial durante la mayor parte del proceso de colisión. De la velocidad inicial, el 13% se imparte a la cuarta bola (que puede verse como un movimiento de 3,3 grados si la quinta bola se mueve 25 grados) y hay una ligera velocidad inversa en las primeras tres bolas, la primera bola tiene la mayor en −7% de la velocidad inicial. Esto separa las bolas, pero vuelven a unirse justo antes cuando regresa la quinta bola. Esto se debe al fenómeno del péndulo de diferentes perturbaciones de ángulo pequeño que tienen aproximadamente el mismo tiempo para regresar al centro.
Las ecuaciones diferenciales hertzianas predicen que si dos bolas golpean a tres, la quinta y la cuarta saldrán con velocidades de 1,14 y 0,80 veces la velocidad inicial. [7] Esto es 2,03 veces más energía cinética en la quinta bola que en la cuarta, lo que significa que la quinta bola oscilaría el doble de alto en la dirección vertical que la cuarta bola. Pero en una cuna de Newton real, la cuarta bola oscila tanto como la quinta bola. Para explicar la diferencia entre la teoría y el experimento, las dos bolas que chocan deben tener al menos ≈ 10 μm de separación (dado el acero, 100 g y 1 m/s). Esto muestra que en el caso común de las bolas de acero, las separaciones inadvertidas pueden ser importantes y deben incluirse en las ecuaciones diferenciales hertzianas, o la solución simple da un resultado más preciso.
Se supuso que las fuerzas de la solución hertziana anterior se propagaban en las bolas inmediatamente, lo que no es el caso. Los cambios repentinos en la fuerza entre los átomos del material se acumulan para formar una onda de presión. Las ondas de presión (sonido) en el acero viajan unos 5 cm en 10 microsegundos, que es aproximadamente 10 veces más rápido que el tiempo entre el impacto de la primera bola y la expulsión de la última. Las ondas de presión se reflejan de ida y vuelta a través de las cinco bolas unas diez veces, aunque se dispersan en un frente de onda menor con más reflexiones. Esto es lo suficientemente rápido para que la solución hertziana no requiera una modificación sustancial para ajustar el retraso en la propagación de la fuerza a través de las bolas. En bolas menos rígidas pero aún muy elásticas, como el caucho, la velocidad de propagación es más lenta, pero la duración de las colisiones es mayor, por lo que la solución hertziana sigue siendo válida. El error introducido por la velocidad limitada de la propagación de la fuerza sesga la solución hertziana hacia la solución simple porque las colisiones no se ven tan afectadas por la inercia de las bolas que están más lejos.
Las bolas de forma idéntica ayudan a que las ondas de presión converjan en el punto de contacto de la última bola: en el punto de impacto inicial, una onda de presión avanza hacia las otras bolas mientras que otra retrocede para reflejarse en el lado opuesto de la primera bola y luego sigue a la primera onda, quedando exactamente el diámetro de una bola por detrás. Las dos ondas se encuentran en el último punto de contacto porque la primera onda se refleja en el lado opuesto de la última bola y se encuentra en el último punto de contacto con la segunda onda. Luego reverberan de ida y vuelta de esta manera unas 10 veces hasta que la primera bola deja de conectarse con la segunda. Luego, las reverberaciones se reflejan en el punto de contacto entre la segunda y la tercera bola, pero aún convergen en el último punto de contacto, hasta que se expulsa la última bola, pero es menos un frente de onda con cada reflexión.
El uso de diferentes tipos de materiales no cambia la acción siempre que el material sea eficientemente elástico. El tamaño de las esferas no cambia los resultados a menos que el aumento de peso exceda el límite elástico del material. Si las bolas sólidas son demasiado grandes, se pierde energía en forma de calor, porque el límite elástico aumenta con el radio elevado a la potencia 1,5, pero la energía que tuvo que absorberse y liberarse aumenta con el cubo del radio. Hacer que las superficies de contacto sean más planas puede superar esto en cierta medida al distribuir la compresión a una mayor cantidad de material, pero puede introducir un problema de alineación. El acero es mejor que la mayoría de los materiales porque permite que la solución simple se aplique con más frecuencia en colisiones después del primer golpe, su rango elástico para almacenar energía sigue siendo bueno a pesar de la mayor energía causada por su peso, y el mayor peso disminuye el efecto de la resistencia del aire.
La aplicación más común es la de un juguete ejecutivo de escritorio . Otro uso es como demostración de física educativa, como ejemplo de conservación del momento y conservación de la energía .

El principio demostrado por el dispositivo, la ley de impactos entre cuerpos, fue demostrado por primera vez por el físico francés Abbé Mariotte en el siglo XVII. [1] [8] Su trabajo sobre el tema fue presentado por primera vez a la Academia Francesa de Ciencias en 1671; se publicó en 1673 como Traité de la percussion ou choc des corps ("Tratado sobre la percusión o el choque de los cuerpos"). [9]
Newton reconoció el trabajo de Mariotte, junto con los de Wren, Wallis y Huygens como pioneros de los experimentos sobre las colisiones de bolas de péndulo, en sus Principia .
Christiaan Huygens utilizó péndulos para estudiar las colisiones. Su obra, De Motu Corporum ex Percussione (Sobre el movimiento de los cuerpos por colisión), publicada póstumamente en 1703, contiene una versión de la primera ley de Newton y analiza la colisión de cuerpos suspendidos, incluidos dos cuerpos de igual masa, en la que el movimiento del cuerpo en movimiento se transfiere al cuerpo en reposo.
Existe mucha confusión sobre los orígenes de la cuna de Newton moderna. Se le atribuye a Marius J. Morin el haber sido el primero en darle nombre y fabricar este popular juguete para ejecutivos . [ cita requerida ] Sin embargo, a principios de 1967, un actor inglés, Simon Prebble , acuñó el nombre de "cuna de Newton" (ahora usado de manera genérica) para la versión de madera fabricada por su compañía, Scientific Demonstrations Ltd. [10] Después de cierta resistencia inicial por parte de los minoristas, primero fueron vendidos por Harrods de Londres, creando así el comienzo de un mercado duradero para los juguetes para ejecutivos. [ cita requerida ] Más tarde, el escultor y futuro director de cine Richard Loncraine creó un diseño cromado muy exitoso para la tienda Gear de Carnaby Street . [ cita requerida ]
El dispositivo de cuna más grande del mundo fue diseñado por MythBusters y consistía en cinco boyas de una tonelada rellenas de hormigón y barras de refuerzo de acero suspendidas de una armadura de acero. [ cita requerida ] Las boyas también tenían una placa de acero insertada entre sus dos mitades para actuar como un "punto de contacto" para transferir la energía; este dispositivo de cuna no funcionó bien porque el hormigón no es elástico, por lo que la mayor parte de la energía se perdió debido a una acumulación de calor en el hormigón. Una versión a menor escala construida por ellos consta de cinco cojinetes de bolas de acero cromado de 15 centímetros (6 pulgadas), cada uno de los cuales pesa 15 kilogramos (33 libras), y es casi tan eficiente como un modelo de escritorio.
El dispositivo de cuna con las bolas de colisión de mayor diámetro en exhibición pública estuvo visible durante más de un año en Milwaukee , Wisconsin, en la tienda minorista American Science and Surplus (ver foto). Cada bola era una pelota de ejercicio inflable de 66 cm (26 pulgadas) de diámetro (envuelta en anillos de acero) y se sostenía desde el techo mediante imanes extremadamente fuertes. Fue desmantelada a principios de agosto de 2010 debido a problemas de mantenimiento. [ cita requerida ]
La cuna de Newton aparece en algunas películas, a menudo como un tropo en el escritorio de un villano principal, como el papel de Paul Newman en The Hudsucker Proxy , Magneto en X-Men y los kriptonianos en Superman II . Se utilizó para representar la posición inquebrantable de la NFL hacia las lesiones en la cabeza en Concussion. [11] También se ha utilizado como una distracción relajante en el escritorio de personajes inteligentes/ansiosos/sensibles como el papel de Henry Winkler en Night Shift , el papel de Dustin Hoffman en Straw Dogs y el papel de Gwyneth Paltrow en Iron Man 2. Apareció de forma más destacada como una serie de vasijas de barro en Rosencrantz y Guildenstern están muertos , y como una fila de sillas burbuja de Eero Aarnio de 1968 con mujeres escasamente vestidas en ellas en Gamer . [12] En Storks , Hunter, el director ejecutivo de Cornerstore, tiene una que no tiene pelotas, sino pajaritos. La cuna de Newton es un artículo en Animal Crossing de Nintendo, donde se la menciona como "juguete ejecutivo". [13] En 2017, un episodio del podcast Omnibus , con el campeón de Jeopardy! Ken Jennings y el músico John Roderick , se centró en la historia de la cuna de Newton. [14] La cuna de Newton también aparece en el escritorio del subdirector de comunicaciones de la Casa Blanca, Sam Seaborn , en The West Wing . En el episodio de Futurama " The Day the Earth Stood Stupid ", se muestra al profesor Hubert Farnsworth con la cabeza en una cuna de Newton y diciendo que es un genio mientras Philip J. Fry pasa caminando.
La banda de rock progresivo Dream Theater utiliza la cuna como imagen en la carátula de su álbum Octavarium de 2005. La banda de rock Jefferson Airplane utilizó la cuna en el álbum Crown of Creation de 1968 como un dispositivo rítmico para crear polirritmos en una pista instrumental. [ cita requerida ]