Métrica de Schwarzschild

Solución a las ecuaciones de campo de Einstein.

En la teoría de la relatividad general de Einstein , la métrica de Schwarzschild (también conocida como solución de Schwarzschild ) es una solución exacta a las ecuaciones de campo de Einstein que describe el campo gravitacional fuera de una masa esférica, bajo el supuesto de que la carga eléctrica de la masa, El momento angular de la masa y la constante cosmológica universal son todos cero. La solución es una aproximación útil para describir objetos astronómicos que giran lentamente, como muchas estrellas y planetas , incluidos la Tierra y el Sol. Fue encontrado por Karl Schwarzschild en 1916.

Según el teorema de Birkhoff , la métrica de Schwarzschild es la solución de vacío esféricamente simétrica más general de las ecuaciones de campo de Einstein. Un agujero negro de Schwarzschild o agujero negro estático es un agujero negro que no tiene carga eléctrica ni momento angular (no giratorio). Un agujero negro de Schwarzschild se describe mediante la métrica de Schwarzschild y no se puede distinguir de ningún otro agujero negro de Schwarzschild excepto por su masa.

El agujero negro de Schwarzschild se caracteriza por un límite esférico circundante, llamado horizonte de sucesos , que se sitúa en el radio de Schwarzschild ( ), a menudo llamado radio de un agujero negro. El límite no es una superficie física, y una persona que cayera a través del horizonte de sucesos (antes de ser destrozada por las fuerzas de las mareas) no notaría ninguna superficie física en esa posición; es una superficie matemática que es importante para determinar las propiedades del agujero negro. Cualquier masa no giratoria y sin carga que sea menor que su radio de Schwarzschild forma un agujero negro. La solución de las ecuaciones de campo de Einstein es válida para cualquier masa M , por lo que en principio (dentro de la teoría de la relatividad general) podría existir un agujero negro de Schwarzschild de cualquier masa si las condiciones se volvieran lo suficientemente favorables para permitir su formación. ${\displaystyle r_{\text{s}}}$

En las proximidades de un agujero negro de Schwarzschild, el espacio se curva tanto que incluso los rayos de luz se desvían, y la luz muy cercana puede desviarse tanto que viaja varias veces alrededor del agujero negro. ^{[1] [2] [3]}

Formulación

La métrica de Schwarzschild es una métrica de Lorentz esféricamente simétrica (aquí, con convención de firma (−, +, +, +) ), definida en (un subconjunto de)

$${\displaystyle \mathbb {R} \times \left(E^{3}-O\right)\cong \mathbb {R} \times (0,\infty )\times S^{2}}$$

las ecuaciones de campo de Einsteinfuera^[4]métrica interior de Schwarzschild ${\displaystyle E^{3}}$ ${\displaystyle S^{2}\subset E^{3}}$ ${\displaystyle \mathrm {SO} (3)=\mathrm {SO} (E^{3})}$ ${\displaystyle E^{3}-O}$ ${\displaystyle S^{2}}$ ${\displaystyle O}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle R}$ ${\displaystyle r>R}$ ${\displaystyle r=R}$

En las coordenadas de Schwarzschild, la métrica de Schwarzschild (o equivalentemente, el elemento de línea para el tiempo adecuado ) tiene la forma ${\displaystyle (t,r,\theta ,\phi )}$

$${\displaystyle {ds}^{2}=-c^{2}\,{d\tau }^{2}=-\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)c^{2}\,dt^{2}+\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)^{-1}\,dr^{2}+r^{2}{d\Omega }^{2},}$$

${\displaystyle {d\Omega }^{2}}$ ${\displaystyle {d\Omega }^{2}=\left(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2}\right)}$

• ${\displaystyle d\tau ^{2}}$es positivo para curvas temporales, en cuyo caso es el tiempo adecuado (tiempo medido por un reloj que se mueve a lo largo de la misma línea mundial con una partícula de prueba ), ${\displaystyle \tau }$
• ${\displaystyle c}$es la velocidad de la luz ,
• ${\displaystyle t}$es, para , la coordenada de tiempo (medida por un reloj ubicado infinitamente lejos del cuerpo masivo y estacionario con respecto a él), ${\displaystyle r>r_{\text{s}}}$
• ${\displaystyle r}$es, para , la coordenada radial (medida como la circunferencia, dividida por 2 π , de una esfera centrada alrededor del cuerpo masivo), ${\displaystyle r>r_{\text{s}}}$
• ${\displaystyle \Omega }$es un punto en las dos esferas , ${\displaystyle S^{2}}$
• ${\displaystyle \theta }$ es la colatitud de (ángulo desde el norte, en unidades de radianes ) definida después de elegir arbitrariamente un eje z , ${\displaystyle \Omega }$
• ${\displaystyle \phi }$es la longitud ( también en radianes) alrededor del eje z elegido , y ${\displaystyle \Omega }$
• ${\displaystyle r_{\text{s}}}$es el radio de Schwarzschild del cuerpo masivo, un factor de escala que está relacionado con su masa por , donde es la constante gravitacional . ^[5] ${\displaystyle M}$ ${\displaystyle r_{\text{s}}={2GM}/{c^{2}}}$ ${\displaystyle G}$

La métrica de Schwarzschild tiene una singularidad para r = 0 , que es una singularidad de curvatura intrínseca. También parece tener una singularidad en el horizonte de sucesos r = r _s . Por lo tanto, según el punto de vista, la métrica se define sólo en la región exterior , sólo en la región interior o en su unión disjunta. Sin embargo, la métrica en realidad no es singular en todo el horizonte de eventos, como se ve en las coordenadas adecuadas (ver más abajo). Para , la métrica de Schwarzschild es asintótica con respecto a la métrica estándar de Lorentz en el espacio de Minkowski. Para casi todos los objetos astrofísicos, la proporción es extremadamente pequeña. Por ejemplo, el radio de Schwarzschild de la Tierra es aproximadamente ${\displaystyle r>r_{\text{s}}}$ ${\displaystyle r<r_{\text{s}}}$ ${\displaystyle r\gg r_{\text{s}}}$ ${\displaystyle {\frac {r_{\text{s}}}{R}}}$ ${\displaystyle r_{\text{s}}^{({\text{Earth}})}}$8,9 mm , mientras que el Sol, que es3,3 × 10 ⁵ veces más masivo ^[6] tiene un radio de Schwarzschild de aproximadamente 3,0 km. La proporción aumenta sólo en las proximidades de agujeros negros y otros objetos ultradensos como las estrellas de neutrones . ${\displaystyle r_{\text{s}}^{({\text{Sun}})}}$

La coordenada radial resulta tener significado físico como la "distancia adecuada entre dos eventos que ocurren simultáneamente en relación con los relojes geodésicos que se mueven radialmente, los dos eventos se encuentran en la misma línea de coordenadas radiales". ^[7]

La solución de Schwarzschild es análoga a la teoría newtoniana clásica de la gravedad que corresponde al campo gravitacional alrededor de una partícula puntual. Incluso en la superficie de la Tierra, las correcciones a la gravedad newtoniana son sólo una parte entre mil millones. ^[8]

Historia

La solución de Schwarzschild lleva el nombre de Karl Schwarzschild , quien encontró la solución exacta en 1915 y la publicó en enero de 1916, ^[9] poco más de un mes después de la publicación de la teoría de la relatividad general de Einstein. Fue la primera solución exacta de las ecuaciones de campo de Einstein además de la solución trivial del espacio plano . Schwarzschild murió poco después de la publicación de su artículo, como resultado de una enfermedad que desarrolló mientras servía en el ejército alemán durante la Primera Guerra Mundial . ^[10]

Johannes Droste en 1916 ^[11] produjo de forma independiente la misma solución que Schwarzschild, utilizando una derivación más simple y directa. ^[12]

En los primeros años de la relatividad general hubo mucha confusión sobre la naturaleza de las singularidades encontradas en las soluciones de Schwarzschild y otras de las ecuaciones de campo de Einstein . En el artículo original de Schwarzschild, puso lo que ahora llamamos horizonte de sucesos en el origen de su sistema de coordenadas. En este artículo también introdujo lo que ahora se conoce como la coordenada radial de Schwarzschild ( r en las ecuaciones anteriores), como variable auxiliar. En sus ecuaciones, Schwarzschild usaba una coordenada radial diferente que era cero en el radio de Schwarzschild.

David Hilbert ^[13] realizó un análisis más completo de la estructura de la singularidad al año siguiente, identificando las singularidades tanto en r = 0 como en r = r _s . Aunque hubo un consenso general de que la singularidad en r = 0 era una singularidad física "genuina", la naturaleza de la singularidad en r = r _s seguía sin estar clara. ^[14]

En 1921 Paul Painlevé y en 1922 Allvar Gullstrand produjeron de forma independiente una métrica, una solución esféricamente simétrica de las ecuaciones de Einstein, que ahora sabemos es la transformación de coordenadas de la métrica de Schwarzschild, coordenadas de Gullstrand-Painlevé , en la que no había singularidad en r = r _s . Sin embargo, no reconocieron que sus soluciones eran simplemente transformaciones de coordenadas y, de hecho, utilizaron su solución para argumentar que la teoría de Einstein estaba equivocada. En 1924, Arthur Eddington produjo la primera transformación de coordenadas ( coordenadas de Eddington-Finkelstein ) que demostró que la singularidad en r = r _s era un artefacto de coordenadas, aunque tampoco parece haber sido consciente de la importancia de este descubrimiento. Posteriormente, en 1932, Georges Lemaître dio una transformación de coordenadas diferente ( coordenadas de Lemaître ) con el mismo efecto y fue el primero en reconocer que esto implicaba que la singularidad en r = r _s no era física. En 1939 , Howard Robertson demostró que un observador en caída libre que descendiera en la métrica de Schwarzschild cruzaría la singularidad r = r _s en una cantidad finita de tiempo propio , aunque esto tomaría una cantidad infinita de tiempo en términos de tiempo coordinado t . ^[14]

En 1950, John Synge produjo un artículo ^{[15] que mostraba la} extensión analítica máxima de la métrica de Schwarzschild, mostrando nuevamente que la singularidad en r = r _s era un artefacto de coordenadas y que representaba dos horizontes. Un resultado similar fue redescubierto más tarde por George Szekeres , ^[16] y de forma independiente Martin Kruskal . ^[17] Las nuevas coordenadas hoy en día conocidas como coordenadas Kruskal-Szekeres eran mucho más simples que las de Synge, pero ambas proporcionaban un único conjunto de coordenadas que cubría todo el espacio-tiempo. Sin embargo, quizás debido a la oscuridad de las revistas en las que se publicaron los artículos de Lemaître y Synge, sus conclusiones pasaron desapercibidas, y muchos de los principales actores en el campo, incluido Einstein, creyeron que la singularidad en el radio de Schwarzschild era física. ^[14] La derivación posterior de Synge de la solución métrica de Kruskal-Szekeres, ^[18] que fue motivada por el deseo de evitar "usar coordenadas 'malas' [Schwarzschild] para obtener coordenadas 'buenas' [Kruskal-Szekeres]", ha sido generalmente subestimado en la literatura, pero fue adoptado por Chandrasekhar en su monografía sobre agujeros negros. ^[19]

Se lograron verdaderos avances en la década de 1960, cuando la formulación matemáticamente rigurosa formulada en términos de geometría diferencial entró en el campo de la relatividad general, permitiendo definiciones más exactas de lo que significa que una variedad lorentziana sea singular. Esto llevó a la identificación definitiva de la singularidad r = r _s en la métrica de Schwarzschild como un horizonte de sucesos , es decir, una hipersuperficie en el espacio-tiempo que puede cruzarse en una sola dirección. ^[14]

Singularidades y agujeros negros

La solución de Schwarzschild parece tener singularidades en r = 0 y r = r _s ; algunos de los componentes métricos "explotan" (implican división por cero o multiplicación por infinito) en estos radios. Dado que se espera que la métrica de Schwarzschild sea válida sólo para aquellos radios mayores que el radio R del cuerpo gravitante, no hay problema siempre que R > r _s . Para las estrellas y planetas ordinarios este es siempre el caso. Por ejemplo, el radio del Sol es aproximadamente700.000  km , mientras que su radio de Schwarzschild es sólo3 kilómetros .

La singularidad en r = r _s divide las coordenadas de Schwarzschild en dos parches desconectados . La solución exterior de Schwarzschild con r > r _s es la que se relaciona con los campos gravitacionales de estrellas y planetas. La solución interior de Schwarzschild con 0 ≤ r < r _s , que contiene la singularidad en r = 0 , está completamente separada del parche exterior por la singularidad en r = r _s . Por lo tanto, las coordenadas de Schwarzschild no proporcionan ninguna conexión física entre los dos parches, que pueden verse como soluciones separadas. Sin embargo , la singularidad en r = r _s es una ilusión; es un ejemplo de lo que se llama singularidad coordinada . Como su nombre lo indica, la singularidad surge de una mala elección de coordenadas o condiciones de coordenadas . Al cambiar a un sistema de coordenadas diferente (por ejemplo , coordenadas de Lemaitre , coordenadas de Eddington-Finkelstein , coordenadas de Kruskal-Szekeres , coordenadas de Novikov o coordenadas de Gullstrand-Painlevé ), la métrica se vuelve regular en r = r _s y puede extender el parche externo a valores de r menor que r _s . Usando una transformación de coordenadas diferente, se puede relacionar el parche externo extendido con el parche interno. ^[20]

Sin embargo, el caso r = 0 es diferente. Si uno pide que la solución sea válida para todos r , se topa con una verdadera singularidad física, o singularidad gravitacional , en el origen. Para ver que se trata de una verdadera singularidad, hay que observar cantidades que son independientes de la elección de las coordenadas. Una de esas cantidades importantes es la invariante de Kretschmann , que viene dada por

${\displaystyle R^{\alpha \beta \gamma \delta }R_{\alpha \beta \gamma \delta }={\frac {12r_{\mathrm {s} }^{2}}{r^{6}}}={\frac {48G^{2}M^{2}}{c^{4}r^{6}}}\,.}$

En r = 0 la curvatura se vuelve infinita, lo que indica la presencia de una singularidad. En este punto, la métrica no se puede ampliar de manera fluida (la invariante de Kretschmann implica segundas derivadas de la métrica), por lo que el espacio-tiempo en sí ya no está bien definido. Además, Sbierski ^[21] demostró que la métrica no se puede ampliar ni siquiera de forma continua. Durante mucho tiempo se pensó que tal solución no era física. Sin embargo, una mayor comprensión de la relatividad general llevó a la comprensión de que tales singularidades eran una característica genérica de la teoría y no sólo un caso especial exótico.

La solución de Schwarzschild, que se considera válida para todo r > 0 , se denomina agujero negro de Schwarzschild . Es una solución perfectamente válida de las ecuaciones de campo de Einstein, aunque (como otros agujeros negros) tiene propiedades bastante extrañas. Para r < r _s la coordenada radial de Schwarzschild r se vuelve temporal y la coordenada temporal t se vuelve espacial . ^[22] Una curva en r constante ya no es una línea de mundo posible de una partícula u observador, ni siquiera si se ejerce una fuerza para tratar de mantenerla allí; Esto ocurre porque el espacio-tiempo se ha curvado tanto que la dirección de causa y efecto (el futuro cono de luz de la partícula ) apunta hacia la singularidad. ^{[ cita necesaria ]} La superficie r = r _s demarca lo que se llama el horizonte de sucesos del agujero negro. Representa el punto a partir del cual la luz ya no puede escapar del campo gravitacional. Cualquier objeto físico cuyo radio R sea menor o igual al radio de Schwarzschild ha sufrido un colapso gravitacional y se ha convertido en un agujero negro.

Coordenadas alternativas

La solución de Schwarzschild se puede expresar en una variedad de diferentes opciones de coordenadas además de las coordenadas de Schwarzschild utilizadas anteriormente. Las diferentes opciones tienden a resaltar diferentes características de la solución. La siguiente tabla muestra algunas opciones populares.

En la tabla anterior, se han introducido algunas abreviaturas para mayor brevedad. La velocidad de la luz c se ha fijado en uno . la notación

${\displaystyle g_{\Omega }=d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}}$

se utiliza para la métrica de una esfera bidimensional de radio unitario. Además, en cada entrada R y T denotan elecciones alternativas de coordenadas radiales y temporales para las coordenadas particulares. Tenga en cuenta que la R o la T pueden variar de una entrada a otra.

Las coordenadas Kruskal-Szekeres tienen la forma a la que se puede aplicar la transformada de Belinski-Zakharov . Esto implica que el agujero negro de Schwarzschild es una forma de solitón gravitacional .

paraboloide de Flamm

Un gráfico del paraboloide de Flamm. No debe confundirse con el concepto no relacionado de pozo de gravedad .

La curvatura espacial de la solución de Schwarzschild para r > r _s se puede visualizar como muestra el gráfico. Considere un corte ecuatorial de tiempo constante a través de la solución de Schwarzschild ( θ =π/2, t = constante) y describamos la posición de una partícula que se mueve en este plano con las coordenadas restantes de Schwarzschild ( r , φ ) . Imaginemos ahora que existe una dimensión euclidiana adicional w , que no tiene realidad física (no forma parte del espacio-tiempo). Luego reemplace el plano ( r , φ ) con una superficie con hoyuelos en la dirección w de acuerdo con la ecuación ( paraboloide de Flamm )

${\displaystyle w=2{\sqrt {r_{\mathrm {s} }\left(r-r_{\mathrm {s} }\right)}}.}$

Esta superficie tiene la propiedad de que las distancias medidas dentro de ella coinciden con las distancias en la métrica de Schwarzschild, porque con la definición de w anterior,

${\displaystyle dw^{2}+dr^{2}+r^{2}\,d\varphi ^{2}=-c^{2}\,d\tau ^{2}={\frac {dr^{2}}{1-{\frac {r_{\mathrm {s} }}{r}}}}+r^{2}\,d\varphi ^{2}}$

Por tanto, el paraboloide de Flamm es útil para visualizar la curvatura espacial de la métrica de Schwarzschild. Sin embargo, no debe confundirse con un pozo de gravedad . Ninguna partícula ordinaria (masiva o sin masa) puede tener una línea de mundo situada sobre el paraboloide, ya que todas las distancias en él son espaciales (esta es una sección transversal en un momento dado, por lo que cualquier partícula que se mueva sobre ella tendría una velocidad infinita ). Un taquión podría tener una línea de mundo espacial que se encuentra enteramente en un solo paraboloide. Sin embargo, incluso en ese caso, su trayectoria geodésica no es la trayectoria que se obtiene a través de una analogía de "lámina de goma" de un pozo gravitacional: en particular, si el hoyuelo se dibuja apuntando hacia arriba en lugar de hacia abajo, la trayectoria geodésica del taquión aún se curva hacia la masa central. , No lejos. Consulte el artículo sobre pozos de gravedad para obtener más información.

El paraboloide de Flamm se puede derivar de la siguiente manera. La métrica euclidiana en las coordenadas cilíndricas ( r , φ , w ) se escribe

${\displaystyle ds^{2}=dw^{2}+dr^{2}+r^{2}\,d\varphi ^{2}\,.}$

Dejando que la superficie se describa mediante la función w = w ( r ) , la métrica euclidiana se puede escribir como

${\displaystyle ds^{2}=\left(1+\left({\frac {dw}{dr}}\right)^{2}\right)\,dr^{2}+r^{2}\,d\varphi ^{2}\,,}$

Comparando esto con la métrica de Schwarzschild en el plano ecuatorial ( θ =π/2) en un tiempo fijo ( t = constante, dt = 0 )

${\displaystyle ds^{2}=\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)^{-1}\,dr^{2}+r^{2}\,d\varphi ^{2}\,,}$

produce una expresión integral para w ( r ) :

${\displaystyle w(r)=\int {\frac {dr}{\sqrt {{\frac {r}{r_{\mathrm {s} }}}-1}}}=2r_{\mathrm {s} }{\sqrt {{\frac {r}{r_{\mathrm {s} }}}-1}}+{\mbox{constant}}}$

cuya solución es el paraboloide de Flamm.

movimiento orbital

Comparación entre la órbita de una partícula de prueba en el espacio-tiempo newtoniano (izquierda) y Schwarzschild (derecha); nótese la precesión absidal a la derecha.

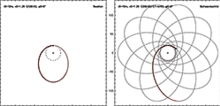
Una partícula que orbita en la métrica de Schwarzschild puede tener una órbita circular estable con r > 3 r _s . Las órbitas circulares con r entre 1,5 r _s y 3 r _s son inestables y no existen órbitas circulares para r < 1,5 r _s . La órbita circular de radio mínimo 1,5 r _s corresponde a una velocidad orbital cercana a la velocidad de la luz. Es posible que una partícula tenga un valor constante de r entre r _s y 1,5 r _s , pero sólo si actúa alguna fuerza para mantenerla allí.

Las órbitas no circulares, como la de Mercurio , permanecen más tiempo en radios pequeños de lo que se esperaría en la gravedad newtoniana . Esto puede verse como una versión menos extrema del caso más dramático en el que una partícula atraviesa el horizonte de sucesos y permanece dentro de él para siempre. Entre el caso de Mercurio y el caso de un objeto que cae más allá del horizonte de sucesos, existen posibilidades exóticas como las órbitas en filo de cuchillo, en las que se puede hacer que el satélite ejecute un número arbitrariamente grande de órbitas casi circulares, después de las cuales vuela hacia afuera.

Simetrías

El grupo de isometría de la métrica de Schwarzchild es , donde es el grupo ortogonal de rotaciones y reflexiones en tres dimensiones, comprende las traslaciones en el tiempo y es el grupo generado por la inversión del tiempo. ${\displaystyle \mathbb {R} \times \mathrm {O} (3)\times \{\pm 1\}}$ ${\displaystyle \mathrm {O} (3)}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \{\pm 1\}}$

Este es, por tanto, el subgrupo del grupo de Poincaré de diez dimensiones que toma el eje del tiempo (trayectoria de la estrella) hacia sí mismo. Omite las traslaciones espaciales (tres dimensiones) y los realces (tres dimensiones). Conserva las traslaciones de tiempo (una dimensión) y las rotaciones (tres dimensiones). Por tanto tiene cuatro dimensiones. Al igual que el grupo Poincaré, tiene cuatro componentes conectados: el componente de la identidad; el componente de tiempo invertido; el componente de inversión espacial; y el componente que está invertido en el tiempo y en el espacio.

Curvaturas

El escalar de curvatura de Ricci y el tensor de curvatura de Ricci son ambos cero. Los componentes distintos de cero del tensor de curvatura de Riemann son ^[25]

${\displaystyle R^{t}{}_{rrt}=2R^{\theta }{}_{r\theta r}=2R^{\phi }{}_{r\phi r}={\frac {r_{\text{s}}}{r^{2}(r_{\text{s}}-r)}},}$

${\displaystyle 2R^{t}{}_{\theta \theta t}=2R^{r}{}_{\theta \theta r}=R^{\phi }{}_{\theta \phi \theta }={\frac {r_{\text{s}}}{r}},}$

${\displaystyle 2R^{t}{}_{\phi \phi t}=2R^{r}{}_{\phi \phi r}=-R^{\theta }{}_{\phi \phi \theta }={\frac {r_{\text{s}}\sin ^{2}(\theta )}{r}},}$

${\displaystyle R^{r}{}_{trt}=-2R^{\theta }{}_{t\theta t}=-2R^{\phi }{}_{t\phi t}=c^{2}{\frac {r_{\text{s}}(r_{\text{s}}-r)}{r^{4}}}}$

No se muestran los componentes que se pueden obtener mediante las simetrías del tensor de Riemann.

Para comprender el significado físico de estas cantidades, resulta útil expresar el tensor de curvatura en forma ortonormal. En una base ortonormal de un observador, los componentes distintos de cero en unidades geométricas son ^[25]

${\displaystyle R^{\hat {r}}{}_{{\hat {t}}{\hat {r}}{\hat {t}}}=-R^{\hat {\theta }}{}_{{\hat {\phi }}{\hat {\theta }}{\hat {\phi }}}=-{\frac {r_{\text{s}}}{r^{3}}},}$

${\displaystyle R^{\hat {\theta }}{}_{{\hat {t}}{\hat {\theta }}{\hat {t}}}=R^{\hat {\phi }}{}_{{\hat {t}}{\hat {\phi }}{\hat {t}}}=-R^{\hat {r}}{}_{{\hat {\theta }}{\hat {r}}{\hat {\theta }}}=-R^{\hat {r}}{}_{{\hat {\phi }}{\hat {r}}{\hat {\phi }}}={\frac {r_{\text{s}}}{2r^{3}}}.}$

Tampoco se muestran los componentes que se pueden obtener mediante las simetrías del tensor de Riemann. Estos resultados son invariantes ante cualquier impulso de Lorentz, por lo que los componentes no cambian para los observadores no estáticos. La ecuación de desviación geodésica muestra que la aceleración de marea entre dos observadores separados por es , por lo que un cuerpo de longitud se estira en la dirección radial por una aceleración aparente y se comprime en las direcciones perpendiculares por . ${\displaystyle \xi ^{\hat {j}}}$ ${\displaystyle D^{2}\xi ^{\hat {j}}/D\tau ^{2}=-R^{\hat {j}}{}_{{\hat {t}}{\hat {k}}{\hat {t}}}\xi ^{\hat {k}}}$ ${\displaystyle L}$ ${\displaystyle (r_{\text{s}}/r^{3})c^{2}L}$ ${\displaystyle -(r_{\text{s}}/(2r^{3}))c^{2}L}$

Ver también

• Derivación de la solución de Schwarzschild
• Métrica de Reissner-Nordström (solución cargada y no giratoria)
• Métrica de Kerr (solución giratoria, descargada)
• Métrica de Kerr-Newman (solución rotativa cargada)
• Agujero negro , una reseña general
• Coordenadas de Schwarzschild
• Coordenadas de Kruskal-Székeres
• Coordenadas de Eddington-Finkelstein
• Coordenadas de Gullstrand-Painlevé
• Coordenadas de Lemaitre (solución de Schwarzschild en coordenadas síncronas )
• Campos de marco en relatividad general (observadores de Lemaître en el vacío de Schwarzschild)
• Ecuación de Tolman-Oppenheimer-Volkoff (ecuaciones métricas y de presión de un cuerpo estático y esféricamente simétrico de material isotrópico)
• longitud de Planck

Notas

1. Luminet, J.-P. (1 de mayo de 1979). "Imagen de un agujero negro esférico con un delgado disco de acreción". Astronomía y Astrofísica . 75 : 228–235. Código bibliográfico : 1979A y A.... 75.. 228L. ISSN  0004-6361.
2. Bozza, V. (22 de noviembre de 2002). "Lentes gravitacionales en el límite del campo fuerte". Revisión física D. 66 (10): 103001. arXiv : gr-qc/0208075 . Código bibliográfico : 2002PhRvD..66j3001B. doi : 10.1103/PhysRevD.66.103001. S2CID  119476658.
3. Sneppen, Albert (9 de julio de 2021). "Reflexiones divergentes alrededor de la esfera de fotones de un agujero negro". Informes científicos . 11 (1): 14247. Código bibliográfico : 2021NatSR..1114247S. doi :10.1038/s41598-021-93595-w. ISSN  2045-2322. PMC 8270963 . PMID  34244573. 
4. Frolov, Valeri; Zelnikov, Andrei (2011). Introducción a la Física de los Agujeros Negros . Oxford. pag. 168.ISBN​ 978-0-19-969229-3.
5. (Landau y Liftshitz 1975) . harv error: no target: CITEREFLandauLiftshitz1975 (help)
6. Tennent, RM, ed. (1971). Libro de datos científicos . Oliver y Boyd . ISBN 0-05-002487-6.
7. Gautreau, R. y Hoffmann, B. (1978). La coordenada radial de Schwarzschild como medida de distancia adecuada. Revisión física D, 17(10), 2552.
8. Ehlers, Jürgen (enero de 1997). "Ejemplos de límites newtonianos de espacios-tiempos relativistas" (PDF) . Gravedad clásica y cuántica . 14 (1A): A119-A126. Código Bib : 1997CQGra..14A.119E. doi :10.1088/0264-9381/14/1A/010. hdl : 11858/00-001M-0000-0013-5AC5-F . S2CID  250804865.
9. Schwarzschild, K. (1916). "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 7 : 189-196. Código Bib :1916SPAW.......189S.Para una traducción, ver Antoci, S.; Loinger, A. (1999). "Sobre el campo gravitacional de un punto de masa según la teoría de Einstein". arXiv : física/9905030 .
10. O'Connor, John J.; Robertson, Edmund F. , "Karl Schwarzschild", Archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews
11. Droste, J. (1917). "El campo de un solo centro en la teoría de la gravitación de Einstein y el movimiento de una partícula en ese campo" (PDF) . Actas de la Real Academia de Artes y Ciencias de los Países Bajos . 19 (1): 197–215. Código bibliográfico : 1917KNAB...19..197D.
12. Kox, AJ (1992). "Relatividad general en los Países Bajos: 1915-1920". En Eisenstaedt, J.; Kox, AJ (eds.). Estudios de Historia de la Relatividad General . Birkhäuser . pag. 41.ISBN​ 978-0-8176-3479-7.
13. Hilbert, David (1924). "Die Grundlagen der Physik". Annalen Matemáticas . Springer-Verlag. 92 (1–2): 1–32. doi :10.1007/BF01448427. S2CID  179177367.
14. Earman, J. (1999). "Los teoremas de singularidad de Penrose-Hawking: historia e implicaciones". En Goenner, H. (ed.). Los mundos en expansión de la relatividad general . Birkhäuser . pag. 236-. ISBN 978-0-8176-4060-6.
15. Synge, JL (1950). "El campo gravitacional de una partícula". Actas de la Real Academia Irlandesa . 53 (6): 83-114. doi :10.1038/164148b0. PMID  18210531. S2CID  4108538.
16. Székeres, G. (1960). "Sobre las singularidades de una variedad de Riemann". Publicaciones Mathematicae Debrecen . 7 : 285. Código Bib : 2002GReGr..34.2001S. doi :10.1023/A:1020744914721. S2CID  118200205.
17. Kruskal, médico (1960). "Extensión máxima de la métrica de Schwarzschild". Revisión física . 119 (5): 1743-1745. Código bibliográfico : 1960PhRv..119.1743K. doi : 10.1103/PhysRev.119.1743.
18. Synge, JL "Universos modelo con simetría esférica". Annali di matematica pura ed applicata 98.1 (1974): 239–255.
19. Chandrasekhar, Subrahmanyan. "La teoría matemática de los agujeros negros, volumen 69 de la serie internacional de monografías sobre física". Clarendon Press, Oxford, Reino Unido 2.3 (1983): 2.
20. Hughston, LP; Tod, KP (1990). Una introducción a la relatividad general . Prensa de la Universidad de Cambridge . Capítulo 19. ISBN 978-0-521-33943-8.
21. Sbierski, enero (2015). "La inextensibilidad C ⁰ del espaciotiempo de Schwarzschild y el diámetro espacial en la geometría lorentziana". arXiv : 1507.00601 [gr-qc].
22. Hora: una guía para el viajero . Prensa de la Universidad de Oxford, incorporada. 1999.ISBN​ 9780199929924. Si nos fijamos en los agujeros negros, la métrica dentro del horizonte de sucesos invierte las coordenadas espaciales y temporales. El radio comienza a actuar como un tiempo y el tiempo comienza a actuar como un espacio.
23. Ni, Wei-Tou, ed. (26 de mayo de 2017). Cien años de relatividad general: del génesis y los fundamentos empíricos a las ondas gravitacionales, la cosmología y la gravedad cuántica. vol. 1. Científico mundial. pag. I-126. ISBN 9789814635141.
24. Eddington, AS (1924). La teoría matemática de la relatividad (2ª ed.). Prensa de la Universidad de Cambridge . pag. 93.
25. Misner, Charles W., Thorne, Kip S., Wheeler, John Archibald, "Gravitación", WH Freeman and Company, Nueva York, ISBN 0-7167-0334-3 

Referencias

• Schwarzschild, K. (1916). "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 7 : 189-196. Código bibliográfico : 1916AbhKP1916..189S.

• Texto del artículo original, en Wikisource
• Traducción: Antoci, S.; Loinger, A. (1999). "Sobre el campo gravitacional de un punto de masa según la teoría de Einstein". arXiv : física/9905030 .
• Un comentario al artículo, que ofrece una derivación más sencilla: Bel, L. (2007). "Über das Gravitationsfeld eines Massenpunktesnach der Einsteinschen Theorie". arXiv : 0709.2257 [gr-qc].

• Schwarzschild, K. (1916). "Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 1 : 424.

• Texto del artículo original, en Wikisource
• Traducción: Antoci, S. (1999). "Sobre el campo gravitacional de una esfera de fluido incompresible según la teoría de Einstein". arXiv : física/9912033 .

• Flamm, L. (1916). "Beiträge zur Einstein'schen Gravitationstheorie". Physikalische Zeitschrift . 17 : 448.
• Adler, R.; Bazin, M.; Schiffer, M. (1975). Introducción a la Relatividad General (2ª ed.). McGraw-Hill . Capítulo 6. ISBN 0-07-000423-4.
• Landau, LD; Lifshitz, EM (1951). La teoría clásica de los campos . Curso de Física Teórica . vol. 2 (cuarta edición revisada en inglés). Prensa de Pérgamo . Capítulo 12. ISBN 0-08-025072-6.
• Misner, CW; Thorne, KS; Wheeler, JA (1970). Gravitación . WH Freeman . Capítulos 31 y 32. ISBN 0-7167-0344-0.
• Weinberg, S. (1972). Gravitación y cosmología: principios y aplicaciones de la teoría general de la relatividad . John Wiley e hijos . Capítulo 8. ISBN 0-471-92567-5.
• Taylor, EF; Wheeler, JA (2000). Explorando los agujeros negros: Introducción a la relatividad general . Addison-Wesley . ISBN 0-201-38423-X.
• Heinzle, JM; Steinbauer, R. (2002). "Observaciones sobre la geometría distribucional de Schwarzschild". Revista de Física Matemática . 43 (3): 1493-1508. arXiv : gr-qc/0112047 . Código bibliográfico : 2002JMP....43.1493H. doi : 10.1063/1.1448684. S2CID  119677857.