
En la historia de la física , el concepto de campos tuvo su origen en el siglo XVIII en una formulación matemática de la ley de gravitación universal de Newton , pero se consideró deficiente ya que implicaba acción a distancia . En 1852, Michael Faraday trató el campo magnético como un objeto físico, razonando sobre líneas de fuerza . James Clerk Maxwell utilizó la conceptualización de Faraday para ayudar a formular su unificación de la electricidad y el magnetismo en su teoría de campos del electromagnetismo .
Con la relatividad especial de Albert Einstein y el experimento de Michelson-Morley se hizo evidente que las ondas electromagnéticas podían viajar en el vacío sin necesidad de un medio o éter luminífero . Einstein también desarrolló la relatividad general , en la que el espacio-tiempo era tratado como un campo y su curvatura era el origen de las interacciones gravitatorias, poniendo fin a la acción a distancia.
En la teoría cuántica de campos , los campos se convierten en los objetos fundamentales de estudio y las partículas son excitaciones de estos campos. Para diferenciarlas de la teoría cuántica de campos, las teorías de campos desarrolladas anteriormente se denominaron teorías de campos clásicas .

El primer registro de explicaciones sobre el funcionamiento de los imanes proviene de la antigua Grecia . [1] Pensadores como Tales de Mileto , Aristóteles y Diógenes Laercio consideraban que los imanes estaban animados y debían tener alma para poder moverse. [1] Empédocles intentó proporcionar una explicación mecánica de por qué los imanes podían influirse entre sí introduciendo el concepto de "efluencias" emanadas por los imanes. [1] Según el libro Quaestiones de Alejandro de Afrodisias de alrededor del año 200 d. C., esta era la opinión de Empédocles: [1]
Sobre la razón por la que la piedra imán atrae al hierro. Empédocles dice que el hierro es atraído hacia la piedra por los efluentes que salen de ambos, y porque los poros de la piedra son proporcionales a los efluentes del hierro. Los efluentes de la piedra agitan y dispersan el aire que se encuentra sobre los poros del hierro y los obstruye, y cuando este se elimina, el hierro es atraído por un flujo de salida concertado. A medida que los efluentes del hierro viajan hacia los poros de la piedra, porque son proporcionales a ellos y encajan en ellos, el propio hierro los sigue y se mueve junto con ellos.
Demócrito tenía una visión similar a la de Empédocles, pero añadió que las efluencias creaban un vacío. Los metales y las rocas también podían contener vacío para ser menos o más atraídos por los imanes. [1]
Esta idea sobrevivió hasta la Revolución Científica . En 1664, René Descartes elaboró su teoría del magnetismo, en la que el flujo de efluvios enrarece el aire, creando diferencias de presión atmosférica. Según Descartes, estos efluvios circulan dentro y alrededor del imán en bucles cerrados. [2]
En la antigüedad, pensadores griegos como Posidonio (1 a. C.) observaron una relación entre las mareas y la posición de la Luna en el cielo. Consideraba que la luz de la Luna tenía influencia en las mareas. [3]
En el siglo IX, Abu Ma'shar al-Balkhi (latinizado como Albumasar) escribió su libro La gran introducción a la ciencia de la astrología ( Kitāb al-madkhal al-kabīr ) y registró la correlación entre las mareas y la Luna, notando que había dos mareas en un día. [4] Como no hay luz de luna cuando la Luna está en el lado opuesto de la Tierra, propuso que la Luna tenía alguna virtud intrínseca que atraía el agua. El Sol tendría algo de esa virtud pero menos que la luna. [3] Este libro fue traducido al latín y fue una referencia para los eruditos medievales europeos. [4] Un escritor que rechazó esta lectura astrológica fue Robert Grosseteste , quien escribió Sobre el flujo y reflujo del mar ( en latín : Questio de fluxu et refluxu maris ), escrito alrededor de 1227, en el que insistió en que la luz de la Luna enrarece el aire produciendo las mareas. [4] Explicó las mareas cuando la Luna está por debajo del horizonte como reflejos de la esfera celeste. [3] Dos teorías coexistieron, la idea de la luz que influye en las mareas y la virtud de Albumasar. Roger Bacon apoyó la idea de Grosseteste, Albertus Magnus apoyó una mezcla de ambas, y otros como Jean Buridan dudaron entre las dos. [3]
En el siglo XVII, Johannes Kepler , que ideó las leyes de Kepler del movimiento planetario , propuso la idea de que el Sol emitía una especie de "especies" invisibles que viajaban instantáneamente y actuaban con mayor fuerza dependiendo de la distancia, el tamaño y la densidad del planeta. Kepler consideró que si el Sol rotara, crearía un remolino de especies que arrastraría a todos los planetas a orbitar a su alrededor. [4] La idea de la rotación del Sol fue confirmada por Galileo Galilei , pero la frecuencia no coincidía con los cálculos de Kepler. [4] Para explicar las mareas, Kepler consideró que las especies se comportarían de manera similar a las fuerzas magnéticas. [4]
Descartes rechazó la teoría de Kepler [4] y también construyó una explicación mecánica de la gravitación basada en las ideas de vórtices, considerando el espacio continuo. [5]

Antes de Newton, sólo existían unas pocas explicaciones mecánicas de la gravedad.
En 1687, los Principia de Newton proporcionaron un marco con el que investigar el movimiento y las fuerzas. Introdujo una definición matemática de la fuerza gravitatoria con su ley de gravitación universal , en la que la fuerza gravitatoria entre dos cuerpos se dirige a lo largo de la línea que separa los cuerpos y su magnitud es proporcional al producto de sus masas dividido por el cuadrado de la distancia entre ellos. [6]
Aunque la explicación de Newton sobre la gravedad tuvo mucho éxito en astronomía, no explicaba cómo podía actuar a distancia e instantáneamente. Newton consideraba que la acción a distancia era:
es un absurdo tan grande que creo que ningún hombre que tenga en cuestiones filosóficas una facultad competente de pensar puede jamás caer en él. [7]
— Isaac Newton, Cartas a Bentley, 1692/3
Gottfried Wilhelm Leibniz se quejó de que la mecánica newtoniana violaba la metafísica de la continuidad según natura non facit saltus , en la que cada causa y efecto deberían estar conectados entre sí. [2] Roger Joseph Boscovich rechazó la postura de Leibniz considerando que los cuerpos tendrían cambios discontinuos en la densidad en los límites y que si entraran en contacto sus velocidades cambiarían discontinuamente. [2]
Los empiristas británicos como John Locke , George Locke y David Hume consideraron que la segunda ley del movimiento de Newton era suficiente, ya que establece una relación causal entre fuerza y aceleración. [2]
Para resolver el problema de la acción a distancia, se desarrollaron teorías del éter. El éter se consideraba un medio aún no detectado y el agente responsable de conducir la fuerza. En una carta a Robert Boyle en 1679, Newton propuso una "sustancia etérea" para explicar la gravedad. [4] Más tarde, en su obra Opticks de 1717, consideró que el éter estaba hecho de corpúsculos impenetrables. [4] [8] El éter newtoniano era muy diluido y elástico. [8] Immanuel Kant consideró que el éter de Newton era inconsistente porque requería fuerzas adicionales entre corpúsculos. [8] Leibniz, por otro lado, consideró un medio continuo. [8]

Un desarrollo importante de las teorías de campos apareció con Leonhard Euler , quien amplió la mecánica newtoniana en su obra Mechanica de 1736. El trabajo de Euler amplió la forma de abordar las rotaciones de cuerpos rígidos, la elasticidad y la mecánica de fluidos. Para describir los fluidos, consideró una función de velocidad de flujo (hoy llamada campo de velocidad) definida en cada punto del espacio. [4] Sin embargo, durante mucho tiempo se consideró que esta función era significativamente diferente de la de las fuerzas de gravedad, ya que solo se definía dentro de un medio y, por lo tanto, se consideraba una cantidad real. [4] La historiadora de la ciencia moderna Mary Hesse atribuyó el origen de la teoría de campos al campo de velocidad de flujo de Euler. [4]
Euler también introdujo entre 1755 y 1759 las especificaciones lagrangianas y eulerianas para el flujo [9] que serían importantes para separar el movimiento de las partículas de las propiedades del campo. [ cita requerida ]
A menudo se cita a Joseph-Louis Lagrange por introducir el concepto de potencial en 1777, y de forma independiente por Adrien-Marie Legendre (1784-1794) y Pierre-Simon Laplace (1782-1799). [10] [11] Lagrange se dio cuenta de que podía introducir un potencial gravitatorio para derivar la fuerza gravitatoria. [10] Esta función fue denominada función potencial por el matemático George Green en 1828 y por Carl Friedrich Gauss en 1840 simplemente como "potencial". [10]
En 1785, Charles-Augustin de Coulomb demostró que la fuerza repulsiva entre dos esferas cargadas eléctricamente obedece a la misma ley de fuerza (hasta un signo) que la ley de gravitación universal de Newton. En 1823, Siméon Denis Poisson introdujo la ecuación de Poisson , explicando las fuerzas eléctricas en términos de un potencial eléctrico . [12] El mismo año, André-Marie Ampère demostró que la fuerza entre longitudes infinitesimales de cables que transportan corriente obedece de manera similar a una ley del cuadrado inverso, de modo que la fuerza se dirige a lo largo de la línea de separación entre los elementos del cable. [8] Estas leyes adolecían del mismo problema de acción a distancia.
En 1800, Thomas Young demostró la naturaleza ondulatoria de la luz mediante el experimento de la doble rendija . Este descubrimiento lo llevó en 1802 a considerar la existencia de un éter luminífero en el que viajaba la luz. [8] Augustin-Jean Fresnel lo consideró un medio elástico. [8] El movimiento de este éter fue descrito matemáticamente por científicos como Claude-Louis Navier (en 1821) y Augustin-Louis Cauchy (en 1828) como medio discreto. [8] Alrededor de 1840, George Stokes y Lord Kelvin extendieron el formalismo para describir un éter continuo utilizando la idea de una teoría del potencial. Este desarrollo fue importante ya que permitió describir cualquier medio deformable en términos de funciones continuas. [8]
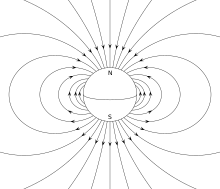
Michael Faraday desarrolló el concepto de líneas de fuerza para describir los fenómenos eléctricos y magnéticos. [13] En 1831, escribe [13]
"Por curvas magnéticas me refiero a las líneas de fuerzas magnéticas, modificadas por la yuxtaposición de polos, que se representarían mediante limaduras de hierro, o aquellas a las que una aguja magnética muy pequeña formaría una tangente".
Proporcionó una definición en 1845, [13]
Pero antes de pasar a ellos, definiré el significado que asocio a ciertos términos que tendré ocasión de utilizar: así, por línea de fuerza magnética , o línea de fuerza magnética , o curva magnética , entiendo el ejercicio de fuerza magnética que se ejerce en las líneas usualmente llamadas curvas magnéticas, y que existen igualmente como pasando desde o hacia polos magnéticos, o formando círculos concéntricos alrededor de una corriente eléctrica. Por línea de fuerza eléctrica , entiendo la fuerza ejercida en las líneas que unen dos cuerpos, actuando uno sobre el otro según los principios de inducción eléctrica estática, que también pueden ser en líneas curvas o rectas.
En su obra, también acuñó el término " campo magnético " en este sentido en 1845, que luego utilizó con frecuencia. [13] Proporcionó una definición clara en 1850, afirmando [13]
Ahora intentaré considerar cuál es la influencia que los cuerpos paramagnéticos y diamagnéticos, considerados como conductores, ejercen sobre las líneas de fuerza de un campo magnético. Cualquier porción de espacio atravesada por líneas de energía magnética puede considerarse como un campo de este tipo , y probablemente no exista espacio sin ellas. La condición del campo puede variar en intensidad de energía de un lugar a otro, ya sea a lo largo de las líneas o a través de ellas; pero será mejor suponer para la presente consideración un campo de fuerza igual en todas partes, y ya he descrito anteriormente cómo esto puede producirse para un cierto espacio limitado.
Faraday no concibió este campo como una mera construcción matemática para calcular las fuerzas entre partículas; al tener sólo una formación matemática rudimentaria, no le servía de nada abstraer la realidad para hacer predicciones cuantitativas. [8] En lugar de eso, conjeturó que había una fuerza que llenaba el espacio donde se generaban los campos electromagnéticos y razonó cualitativamente sobre estas fuerzas con líneas de fuerza: [14]
Lo importante para la definición de estas líneas es que representan una cantidad determinada e inmutable de fuerza. Por lo tanto, aunque sus formas, tal como existen entre dos o más centros o fuentes de poder, pueden variar mucho, y también el espacio a través del cual pueden trazarse, la suma de poder contenida en cualquier sección de una porción dada de las líneas es exactamente igual a la suma de poder en cualquier otra sección de las mismas líneas, por muy alterada que sea su forma o por muy convergentes o divergentes que sean en segundo lugar.
Sin embargo, Faraday nunca utilizó el término " campo eléctrico " explícitamente. [13] No obstante, los conocimientos de Faraday sobre el comportamiento de los campos magnéticos resultarían invaluables para el desarrollo del electromagnetismo y la teoría de campos.
En 1845, Lord Kelvin formalizó las similitudes matemáticas entre los campos de los fenómenos electromagnéticos y el trabajo de Joseph Fourier sobre el calor; y en 1947 entre la conducción eléctrica y la elasticidad. [2] Estas similitudes llevaron a Lord Kelvin a proponer una definición formal del campo magnético [2] en 1851: [4]
Cualquier espacio en cada punto del cual hay una fuerza magnética finita se llama 'campo de fuerza magnética' o (entendiendo por magnético) simplemente 'campo de fuerza', o a veces 'campo magnético'.
— Lord Kelvin, Sobre la teoría de la inducción magnética en sustancias cristalinas y no cristalinas, [15]
Kelvin también introdujo el concepto de potencial vectorial magnético . [16]

En 1864, James Clerk Maxwell publicó " Una teoría dinámica del campo electromagnético ", en la que recopiló todas las ecuaciones conocidas de electricidad y magnetismo. Las ecuaciones de Maxwell dieron lugar a una ecuación de onda electromagnética con ondas que se propagaban en el vacío a la velocidad de la luz . Describe su investigación como
(3) La teoría que propongo puede, por tanto, llamarse teoría del campo electromagnético , porque tiene que ver con el espacio en la vecindad de los cuerpos eléctricos y magnéticos, y puede llamarse teoría dinámica , porque supone que en ese espacio hay materia en movimiento, por la cual se producen los fenómenos electromagnéticos observados.
(4) El campo electromagnético es aquella parte del espacio que contiene y rodea a los cuerpos en condiciones eléctricas o magnéticas.
En Tratado sobre electricidad y magnetismo de 1873, escribe: "el campo eléctrico es la porción de espacio en la vecindad de los cuerpos electrificados, considerados con referencia a los fenómenos eléctricos". Y para los campos magnéticos
Parece, pues, que en el espacio que rodea a un cable que transmite una corriente eléctrica, actúan sobre un imán fuerzas que dependen de la posición del cable y de la intensidad de la corriente. El espacio en el que actúan estas fuerzas puede considerarse, pues, como un campo magnético y podemos estudiarlo de la misma manera que ya hemos estudiado el campo en las proximidades de los imanes ordinarios, siguiendo el curso de las líneas de fuerza magnética y midiendo la intensidad de la fuerza en cada punto.
Maxwell tuvo que conformarse con la idea de un éter luminífero . Escribió [16]
Tenemos, pues, alguna razón para creer, a partir de los fenómenos de la luz y del calor, que existe un medio etéreo que llena el espacio y permea los cuerpos, capaz de ponerse en movimiento y de transmitir ese movimiento de una parte a otra, y de comunicar ese movimiento a la materia bruta para calentarla y afectarla de diversas maneras.
Maxwell tenía dudas sobre la naturaleza de los campos, ya que consideraba que el éter era un medio mecánico capaz de transportar energía. [2] En 1868, Carl Neumann discutió la idea de que el campo electromagnético era un campo de energía independiente. [2]
En 1887, Heinrich Hertz publicó su evidencia experimental de la existencia de ondas electromagnéticas. [2]
El experimento de Michelson-Morley de 1887 intentó demostrar que las radiaciones electromagnéticas eran oscilaciones de un éter luminífero , pero el resultado fue negativo, lo que indicaba que la radiación podía viajar en el vacío. Para explicar este fenómeno, Albert Einstein desarrolló su teoría de la relatividad especial (1905) que resolvió los conflictos entre la mecánica clásica y el electromagnetismo. Einstein introdujo la transformación de Lorentz para los campos electromagnéticos entre sistemas de referencia.
Einstein desarrolló las ecuaciones de campo de Einstein de la relatividad general en 1915, coherentes con la relatividad especial y que podían explicar la gravitación en términos de una teoría de campo del espacio-tiempo . Esto eliminó la necesidad de un éter gravitacional.
En 1918, Emmy Noether publica su teorema sobre las relaciones entre simetrías y leyes de conservación. [17] El teorema de Noether fue adaptado a la relatividad general así como a las teorías de campo no relativistas. [18]
Los intentos de crear una teoría de campo unificado basada en la física clásica son las teorías clásicas de campo unificado. Durante los años entre las dos guerras mundiales , la idea de unificar la gravedad con el electromagnetismo fue perseguida activamente por varios matemáticos y físicos como Einstein, Theodor Kaluza , [19] Hermann Weyl , [20] Arthur Eddington , [21] Gustav Mie [22] y Ernst Reichenbacher. [23]
Los primeros intentos de crear dicha teoría se basaron en la incorporación de campos electromagnéticos a la geometría de la relatividad general. En 1918, Weyl propuso la primera geometrización del campo electromagnético. [24] En este trabajo, Weyl acuñó el término teoría de calibre . [25] Weyl, en un intento de generalizar las ideas geométricas de la relatividad general para incluir el electromagnetismo, conjeturó que Eichinvarianz o invariancia bajo el cambio de escala (o "calibre") también podría ser una simetría local de la relatividad general.
En 1919, Kaluza sugirió la idea de un enfoque de cinco dimensiones. [24] A partir de ahí, se desarrolló una teoría llamada teoría de Kaluza-Klein . Intenta unificar la gravitación y el electromagnetismo en un espacio-tiempo de cinco dimensiones. Hay varias formas de extender el marco de representación para una teoría de campo unificado que han sido consideradas por Einstein y otros investigadores. Estas extensiones en general se basan en dos opciones. [24] La primera opción se basa en relajar las condiciones impuestas en la formulación original, y la segunda se basa en introducir otros objetos matemáticos en la teoría. [24] Un ejemplo de la primera opción es relajar las restricciones al espacio-tiempo de cuatro dimensiones al considerar representaciones de dimensiones superiores. [24] Esto se utiliza en la teoría de Kaluza-Klein. Para el segundo, el ejemplo más destacado surge del concepto de conexión afín que se introdujo en la relatividad general principalmente a través del trabajo de Tullio Levi-Civita y Weyl. [24]
El desarrollo posterior de la teoría cuántica de campos cambió el enfoque de la búsqueda de la teoría unificada de campos, pasando de la descripción clásica a la cuántica. Debido a eso, muchos físicos teóricos abandonaron la búsqueda de una teoría clásica de campos unificados. [24] La teoría cuántica de campos incluiría la unificación de otras dos interacciones fundamentales de la naturaleza, la fuerza nuclear fuerte y la débil , que actúan a nivel subatómico. [26] [27]
Los campos se convierten en el objeto fundamental de estudio en la teoría cuántica de campos. Matemáticamente, los campos cuánticos se formalizan como distribuciones con valores de operador. [28] Aunque no existe un método directo para medir los campos en sí, el marco afirma que todas las partículas son "excitaciones" de estos campos. Por ejemplo: mientras que la teoría de Maxwell del electromagnetismo clásico describe la luz como una onda que se autopropaga en el campo electromagnético, en la electrodinámica cuántica la luz es la partícula sin masa del bosón de calibre llamada fotón . Además, no es necesario que se conserve el número de partículas en un sistema aislado; un ejemplo de un proceso para el que esto es así es la radiación de frenado . Se obtiene una comprensión más detallada del marco estudiando la densidad lagrangiana de una teoría de campos que codifica la información de sus interacciones de partículas permitidas. [29]
{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )