Área de un círculo

Concepto en geometría

En geometría , el área encerrada por un círculo de radio r es π r ² . Aquí la letra griega π representa la relación constante entre la circunferencia de cualquier círculo y su diámetro , aproximadamente igual a 3,14159.

Un método para derivar esta fórmula, que se originó con Arquímedes , implica considerar el círculo como el límite de una secuencia de polígonos regulares con un número creciente de lados. El área de un polígono regular es la mitad de su perímetro multiplicado por la distancia desde su centro a sus lados , y como la secuencia tiende a un círculo, la fórmula correspondiente (que el área es la mitad de la circunferencia por el radio) es, A = ⁠1/2⁠ × 2π r × r , es válido para un círculo.

Terminología

Aunque en contextos informales se suele hacer referencia a ella como el área de un círculo, en sentido estricto, el término disco se refiere a la región interior del círculo, mientras que círculo se reserva únicamente para el límite, que es una curva y no cubre ningún área en sí. Por lo tanto, el área de un disco es la frase más precisa para el área encerrada por un círculo.

Historia

Las matemáticas modernas pueden obtener el área utilizando los métodos del cálculo integral o su descendencia más sofisticada, el análisis real . Sin embargo, el área de un disco fue estudiada por los antiguos griegos . Eudoxo de Cnido en el siglo V a. C. había descubierto que el área de un disco es proporcional a su radio al cuadrado. ^[1] Arquímedes utilizó las herramientas de la geometría euclidiana para demostrar que el área dentro de un círculo es igual a la de un triángulo rectángulo cuya base tiene la longitud de la circunferencia del círculo y cuya altura es igual al radio del círculo en su libro Medición de un círculo . La circunferencia es 2 π r , y el área de un triángulo es la mitad de la base por la altura, lo que da el área π  r ² para el disco. Antes de Arquímedes, Hipócrates de Quíos fue el primero en demostrar que el área de un disco es proporcional al cuadrado de su diámetro, como parte de su cuadratura de la luna de Hipócrates , ^[2] pero no identificó la constante de proporcionalidad .

Argumentos históricos

Históricamente se han presentado diversos argumentos para establecer la ecuación con distintos grados de rigor matemático. El más famoso de ellos es el método de extenuación de Arquímedes , uno de los primeros usos del concepto matemático de límite , así como el origen del axioma de Arquímedes que sigue siendo parte del tratamiento analítico estándar del sistema de números reales . La prueba original de Arquímedes no es rigurosa según los estándares modernos, porque supone que podemos comparar la longitud del arco de un círculo con la longitud de una secante y una tangente, y afirmaciones similares sobre el área, como geométricamente evidentes. ${\displaystyle A=\pi r^{2}}$

Usando polígonos

El área de un polígono regular es la mitad de su perímetro multiplicado por la apotema . A medida que aumenta el número de lados del polígono regular, el polígono tiende a ser un círculo y la apotema tiende al radio. Esto sugiere que el área de un disco es la mitad de la circunferencia de su círculo delimitador multiplicado por el radio. ^[3]

Prueba de Arquímedes

Siguiendo el argumento de Arquímedes en La medida del círculo (c. 260 a. C.), comparemos el área encerrada por un círculo con un triángulo rectángulo cuya base tiene la longitud de la circunferencia del círculo y cuya altura es igual al radio del círculo. Si el área del círculo no es igual a la del triángulo, entonces debe ser mayor o menor. Eliminamos cada una de estas posibilidades por contradicción, dejando la igualdad como la única posibilidad. Usamos los polígonos regulares de la misma manera.

No mayor

Círculo con un cuadrado y un octógono inscritos, mostrando el área vacía

Supóngase que el área C encerrada por el círculo es mayor que el área T  = cr /2 del triángulo. Sea E la cantidad sobrante. Inscriba un cuadrado en el círculo, de modo que sus cuatro vértices queden sobre el círculo. Entre el cuadrado y el círculo hay cuatro segmentos. Si el área total de esos espacios, G ₄ , es mayor que E , divida cada arco por la mitad. Esto convierte al cuadrado inscrito en un octógono inscrito y produce ocho segmentos con un espacio total menor, G ₈ . Continúe dividiendo hasta que el área total del espacio, G _n , sea menor que E . Ahora el área del polígono inscrito, P _n  = C  −  G _n , debe ser mayor que la del triángulo.

${\displaystyle {\begin{aligned}E&{}=C-T\\&{}>G_{n}\\P_{n}&{}=C-G_{n}\\&{}>C-E\\P_{n}&{}>T\end{aligned}}}$

Pero esto genera una contradicción, como sigue: si se traza una perpendicular desde el centro hasta el punto medio de un lado del polígono, su longitud, h , es menor que el radio del círculo. Además, si cada lado del polígono tiene una longitud s , la suma de los lados es ns , que es menor que la circunferencia del círculo. El área del polígono consta de n triángulos iguales con una altura h y una base s , por lo que es igual a nhs /2. Pero como h  <  r y ns  <  c , el área del polígono debe ser menor que el área del triángulo, cr /2, lo que constituye una contradicción. Por lo tanto, nuestra suposición de que C podría ser mayor que T debe ser errónea.

No menos

Círculo con cuadrado y octógono circunscrito, mostrando área de brecha

Supóngase que el área encerrada por el círculo es menor que el área T del triángulo. Sea D la cantidad del déficit. Circunscriba un cuadrado de modo que el punto medio de cada arista se encuentre en el círculo. Si el área total del espacio entre el cuadrado y el círculo, G ₄ , es mayor que D , corte las esquinas con tangentes circulares para formar un octógono circunscrito y continúe cortando hasta que el área del espacio sea menor que D . El área del polígono, P _n , debe ser menor que T .

${\displaystyle {\begin{aligned}D&{}=T-C\\&{}>G_{n}\\P_{n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&{}<T\end{aligned}}}$

Esto también genera una contradicción, ya que una perpendicular al punto medio de cada lado del polígono es un radio de longitud r . Y como la longitud total de los lados es mayor que la circunferencia, el polígono consta de n triángulos idénticos con un área total mayor que T. Nuevamente tenemos una contradicción, por lo que nuestra suposición de que C podría ser menor que T también debe ser errónea.

Por lo tanto, debe ser el caso que el área encerrada por el círculo sea exactamente la misma que el área del triángulo. Con esto concluye la prueba.

Prueba de reordenamiento

Área del círculo por reordenamiento

Gráficas de lado ,  s ; apotema ,  a ; y área ,  A de polígonos regulares de n lados y radio circunscrito 1, con la base ,  b de un rectángulo con la misma área. La línea verde muestra el caso n = 6 .

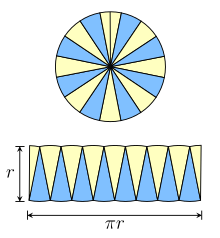
Siguiendo a Satō Moshun (Smith & Mikami 1914, pp. 130–132), Nicolás de Cusa ^[4] y Leonardo da Vinci (Beckmann 1976, p. 19), podemos utilizar polígonos regulares inscritos de una manera diferente. Supongamos que inscribimos un hexágono . Cortamos el hexágono en seis triángulos partiéndolo desde el centro. Dos triángulos opuestos tocan dos diámetros comunes; deslízalos a lo largo de uno de modo que los bordes radiales sean adyacentes. Ahora forman un paralelogramo , con los lados del hexágono formando dos bordes opuestos, uno de los cuales es la base, s . Dos bordes radiales forman lados inclinados, y la altura, h es igual a su apotema (como en la prueba de Arquímedes). De hecho, también podemos ensamblar todos los triángulos en un gran paralelogramo poniendo pares sucesivos uno al lado del otro. Lo mismo es cierto si lo aumentamos a ocho lados y así sucesivamente. Para un polígono con 2 n lados, el paralelogramo tendrá una base de longitud ns y una altura h . A medida que aumenta el número de lados, la longitud de la base del paralelogramo se acerca a la mitad de la circunferencia del círculo y su altura se acerca al radio del círculo. En el límite, el paralelogramo se convierte en un rectángulo con ancho π r y altura r .

Pruebas modernas

Existen varias definiciones equivalentes de la constante π. La definición convencional en geometría precálculo es la relación entre la circunferencia de un círculo y su diámetro:

${\displaystyle \pi ={\frac {C}{D}}.}$

Sin embargo, debido a que la circunferencia de un círculo no es un concepto analítico primitivo, esta definición no es adecuada en los tratamientos rigurosos modernos. Una definición moderna estándar es que π es igual al doble de la raíz menos positiva de la función coseno o, equivalentemente, el semiperiodo de la función seno (o coseno). La función coseno se puede definir como una serie de potencias o como la solución de una cierta ecuación diferencial . Esto evita cualquier referencia a círculos en la definición de π , de modo que las afirmaciones sobre la relación de π con la circunferencia y el área de los círculos son en realidad teoremas, en lugar de definiciones, que se desprenden de las definiciones analíticas de conceptos como "área" y "circunferencia".

Las definiciones analíticas parecen ser equivalentes, si se acepta que la circunferencia del círculo se mide como una curva rectificable por medio de la integral

${\displaystyle C=2\int _{-R}^{R}{\frac {R\,dx}{\sqrt {R^{2}-x^{2}}}}=2R\int _{-1}^{1}{\frac {dx}{\sqrt {1-x^{2}}}}.}$

La integral que aparece a la derecha es una integral abeliana cuyo valor es un semiperiodo de la función seno , igual a π . Por lo tanto, se considera que es verdadera como teorema. ${\displaystyle C=2\pi R=\pi D}$

Varios de los argumentos que siguen utilizan sólo conceptos del cálculo elemental para reproducir la fórmula , pero en muchos casos, para considerarlos como pruebas reales, se basan implícitamente en el hecho de que se pueden desarrollar funciones trigonométricas y la constante fundamental π de una manera que es totalmente independiente de su relación con la geometría. Hemos indicado, cuando ha sido apropiado, cómo cada una de estas pruebas puede hacerse totalmente independiente de toda trigonometría, pero en algunos casos eso requiere ideas matemáticas más sofisticadas que las que ofrece el cálculo elemental. ${\displaystyle A=\pi r^{2}}$

Prueba de cebolla

Área del disco mediante integración de anillos

Utilizando el cálculo, podemos sumar el área de forma incremental, dividiendo el disco en anillos concéntricos delgados como las capas de una cebolla . Este es el método de integración de capas en dos dimensiones. Para un anillo infinitesimalmente delgado de la "cebolla" de radio t , el área acumulada es 2 π t dt , la longitud circunferencial del anillo multiplicada por su ancho infinitesimal (se puede aproximar este anillo mediante un rectángulo con ancho=2 π t y altura= dt ). Esto da una integral elemental para un disco de radio r .

${\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}2\pi t\,dt\\&{}=2\pi \left[{\frac {t^{2}}{2}}\right]_{0}^{r}\\&{}=\pi r^{2}.\end{aligned}}}$

Esto se justifica rigurosamente por la regla de sustitución multivariante en coordenadas polares. Es decir, el área viene dada por una doble integral de la función constante 1 sobre el propio disco. Si D denota el disco, entonces la doble integral se puede calcular en coordenadas polares de la siguiente manera:

${\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt\ d\theta \\&{}=\int _{0}^{r}\int _{0}^{2\pi }t\ d\theta \ dt\\&{}=\int _{0}^{r}\left[t\theta \right]_{0}^{2\pi }dt\\&{}=\int _{0}^{r}2\pi t\,dt\\\end{aligned}}}$

que es el mismo resultado que el obtenido anteriormente.

Una justificación rigurosa equivalente, sin depender de las coordenadas especiales de la trigonometría, utiliza la fórmula de coarea . Definamos una función por . Nótese que ρ es una función de Lipschitz cuyo gradiente es un vector unitario ( casi en todas partes ). Sea D el disco en . Demostraremos que , donde es la medida de Lebesgue bidimensional en . Supondremos que la medida de Hausdorff unidimensional del círculo es , la circunferencia del círculo de radio r . (Esto puede tomarse como la definición de circunferencia). Entonces, por la fórmula de coarea, ${\displaystyle \rho :\mathbb {R} ^{2}\to \mathbb {R} }$ ${\textstyle \rho (x,y)={\sqrt {x^{2}+y^{2}}}}$ ${\displaystyle |\nabla \rho |=1}$ ${\displaystyle \rho <1}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle {\mathcal {L}}^{2}(D)=\pi }$ ${\displaystyle {\mathcal {L}}^{2}}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \rho =r}$ ${\displaystyle 2\pi r}$

${\displaystyle {\begin{aligned}{\mathcal {L}}^{2}(D)&=\iint _{D}|\nabla \rho |\,d{\mathcal {L}}^{2}\\&=\int _{\mathbb {R} }{\mathcal {H}}^{1}(\rho ^{-1}(r)\cap D)\,dr\\&=\int _{0}^{1}{\mathcal {H}}^{1}(\rho ^{-1}(r))\,dr\\&=\int _{0}^{1}2\pi r\,dr=\pi .\end{aligned}}}$

Prueba de triángulo

Círculo desenrollado para formar un triángulo.

El círculo y el triángulo son iguales en área.

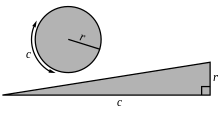
De manera similar a la prueba de la cebolla descrita anteriormente, podríamos aprovechar el cálculo de una manera diferente para llegar a la fórmula del área de un disco. Consideremos que desenrollamos los círculos concéntricos hasta formar tiras rectas. Esto formará un triángulo rectángulo con r como su altura y 2 π r (siendo la rodaja exterior de la cebolla) como su base.

Encontrar el área de este triángulo dará el área del disco.

${\displaystyle {\begin{aligned}{\text{Area}}&{}={\frac {1}{2}}\cdot {\text{base}}\cdot {\text{height}}\\&{}={\frac {1}{2}}\cdot 2\pi r\cdot r\\&{}=\pi r^{2}\end{aligned}}}$

Los ángulos opuestos y adyacentes de este triángulo están respectivamente en grados 9,0430611..., 80,956939... y en radianes 0,1578311... OEIS : A233527 , 1,4129651... OEIS : A233528 .

Explícitamente, imaginamos dividir un círculo en triángulos, cada uno con una altura igual al radio del círculo y una base infinitesimalmente pequeña. El área de cada uno de estos triángulos es igual a . Sumando (integrando) todas las áreas de estos triángulos, llegamos a la fórmula para el área del círculo: ${\displaystyle 1/2\cdot r\cdot du}$

${\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{2\pi r}{\frac {1}{2}}r\,du\\&{}=\left[{\frac {1}{2}}ru\right]_{0}^{2\pi r}\\&{}=\pi r^{2}.\end{aligned}}}$

Esto también se puede justificar mediante una doble integral de la función constante 1 sobre el disco invirtiendo el orden de integración y utilizando un cambio de variables en la integral iterada anterior:

${\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt\ d\theta \\&{}=\int _{0}^{2\pi }\int _{0}^{r}t\ dt\ d\theta \\&{}=\int _{0}^{2\pi }{\frac {1}{2}}r^{2}\ d\theta \\\end{aligned}}}$

Al realizar la sustitución la integral se convierte en ${\displaystyle u=r\theta ,\ du=r\ d\theta }$

${\displaystyle \int _{0}^{2\pi r}{\frac {1}{2}}{\frac {r^{2}}{r}}du=\int _{0}^{2\pi r}{\frac {1}{2}}r\ du}$

que es el mismo que el resultado anterior.

La prueba del triángulo se puede reformular como una aplicación del teorema de Green en forma de flujo-divergencia (es decir, una versión bidimensional del teorema de divergencia ), de manera que se evite toda mención de la trigonometría y la constante π . Consideremos el campo vectorial en el plano. Por lo tanto, la divergencia de r es igual a dos y, por lo tanto, el área de un disco D es igual a ${\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {j} }$

${\displaystyle A={\frac {1}{2}}\iint _{D}\operatorname {div} \mathbf {r} \,dA.}$

Según el teorema de Green, esto es lo mismo que el flujo saliente de r a través del círculo que delimita D :

${\displaystyle A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot \mathbf {n} \,ds}$

donde n es la normal unitaria y ds es la medida de la longitud del arco. Para un círculo de radio R centrado en el origen, tenemos y , por lo que la igualdad anterior es ${\displaystyle |\mathbf {r} |=R}$ ${\displaystyle \mathbf {n} =\mathbf {r} /R}$

${\displaystyle A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot {\frac {\mathbf {r} }{R}}\,ds={\frac {R}{2}}\oint _{\partial D}\,ds.}$

La integral de ds sobre todo el círculo es simplemente la longitud del arco, que es su circunferencia, por lo que esto demuestra que el área A encerrada por el círculo es igual a veces la circunferencia del círculo. ${\displaystyle \partial D}$ ${\displaystyle R/2}$

Otra prueba que utiliza triángulos considera que el área encerrada por un círculo está formada por un número infinito de triángulos (es decir, cada triángulo tiene un ángulo de d𝜃 en el centro del círculo), cada uno con un área de ⁠1/2⁠ · r ² · d𝜃 (derivado de la expresión para el área de un triángulo: ⁠1/2⁠ · a · b · sen 𝜃 = ⁠1/2⁠ · r · r · sen( d𝜃 ) = ⁠1/2⁠ · r ² · d𝜃 ). Nótese que sin( d𝜃 ) ≈ d𝜃 debido a la aproximación de ángulos pequeños . Al sumar las áreas de los triángulos, se puede encontrar la expresión para el área del círculo: $${\displaystyle {\begin{aligned}\mathrm {Area} &{}=\int _{0}^{2\pi }{\frac {1}{2}}r^{2}\,d\theta \\&{}=\left[{\frac {1}{2}}r^{2}\theta \right]_{0}^{2\pi }\\&{}=\pi r^{2}.\end{aligned}}}$$

Prueba del semicírculo

Nótese que el área de un semicírculo de radio r se puede calcular mediante la integral . ${\textstyle \int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx}$

Un semicírculo de radio r

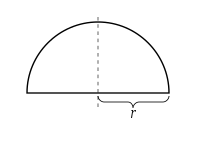
Por sustitución trigonométrica , sustituimos , por lo tanto ${\displaystyle x=r\sin \theta }$ ${\displaystyle dx=r\cos \theta \,d\theta .}$ $${\displaystyle {\begin{aligned}\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx&=\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}{\sqrt {r^{2}\left(1-\sin ^{2}\theta \right)}}\cdot r\cos \theta \,d\theta \\&=2r^{2}\int _{0}^{\frac {\pi }{2}}\cos ^{2}\theta \,d\theta \\&={\frac {\pi r^{2}}{2}}.\end{aligned}}}$$

El último paso se sigue ya que la identidad trigonométrica implica que y tienen integrales iguales en el intervalo , utilizando la integración por sustitución . Pero por otro lado, como , la suma de las dos integrales es la longitud de ese intervalo, que es . En consecuencia, la integral de es igual a la mitad de la longitud de ese intervalo, que es . ${\displaystyle \cos(\theta )=\sin(\pi /2-\theta )}$ ${\displaystyle \cos ^{2}\theta }$ ${\displaystyle \sin ^{2}\theta }$ ${\displaystyle [0,\pi /2]}$ ${\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1}$ ${\displaystyle \pi /2}$ ${\displaystyle \cos ^{2}\theta }$ ${\displaystyle \pi /4}$

Por lo tanto, el área de un círculo de radio r , que es el doble del área del semicírculo, es igual a . ${\displaystyle 2\cdot {\frac {\pi r^{2}}{2}}=\pi r^{2}}$

Esta prueba en particular puede parecer una petición de principio, si las funciones seno y coseno involucradas en la sustitución trigonométrica se consideran definidas en relación con círculos. Sin embargo, como se señaló anteriormente, es posible definir seno, coseno y π de una manera que sea totalmente independiente de la trigonometría, en cuyo caso la prueba es válida por la fórmula de cambio de variables y el teorema de Fubini , suponiendo las propiedades básicas del seno y el coseno (que también se pueden demostrar sin suponer nada sobre su relación con los círculos).

Desigualdad isoperimétrica

El círculo es la curva cerrada de menor perímetro que encierra la máxima área. Esto se conoce como desigualdad isoperimétrica , que establece que si una curva de Jordan rectificable en el plano euclidiano tiene perímetro C y encierra un área A (por el teorema de la curva de Jordan ) entonces

${\displaystyle 4\pi A\leq C^{2}.}$

Además, la igualdad se cumple en esta desigualdad si y sólo si la curva es un círculo, en cuyo caso y . ${\displaystyle A=\pi r^{2}}$ ${\displaystyle C=2\pi r}$

Aproximación rápida

Los cálculos que utilizó Arquímedes para aproximar numéricamente el área fueron laboriosos, y se detuvo en un polígono de 96 lados. Un método más rápido utiliza las ideas de Willebrord Snell ( Cyclometricus , 1621), desarrolladas posteriormente por Christiaan Huygens ( De Circuli Magnitudine Inventa , 1654), descritas en Gerretsen y Verdenduin (1983, pp. 243-250).

El método de duplicación de Arquímedes

Dado un círculo, sea u _n el perímetro de un n- gono regular inscrito, y sea U _n el perímetro de un n- gono regular circunscrito. Entonces u _n y U _n son límites inferior y superior para la circunferencia del círculo que se vuelven cada vez más agudos a medida que n aumenta, y su promedio ( u _n + U _n )/2 es una aproximación especialmente buena a la circunferencia. Para calcular u _n y U _n para n grandes , Arquímedes derivó las siguientes fórmulas de duplicación:

${\displaystyle u_{2n}={\sqrt {U_{2n}u_{n}}}}$   ( media geométrica ), y

${\displaystyle U_{2n}={\frac {2U_{n}u_{n}}{U_{n}+u_{n}}}}$    ( media armónica ).

Partiendo de un hexágono, Arquímedes duplicó n cuatro veces para obtener un 96-gono, lo que le dio una buena aproximación a la circunferencia del círculo.

En notación moderna, podemos reproducir su cálculo (e ir más allá) de la siguiente manera. Para un círculo unitario, un hexágono inscrito tiene u ₆  = 6, y un hexágono circunscrito tiene U ₆  = 4 √ 3 . Duplicando siete veces obtenemos

(Aquí ⁠tu _n + tu _n/2⁠ se aproxima a la circunferencia del círculo unitario, que es 2 π , por lo que ⁠tu _n + tu _n/4⁠ se aproxima a π .)

La última entrada de la tabla tiene ³⁵⁵ ⁄ ₁₁₃ como una de sus mejores aproximaciones racionales ; es decir, no hay mejor aproximación entre los números racionales con denominador hasta 113. El número ³⁵⁵ ⁄ ₁₁₃ es también una excelente aproximación a π , atribuida al matemático chino Zu Chongzhi , quien lo nombró Milü . ^[5] Esta aproximación es mejor que cualquier otro número racional con denominador menor que 16.604. ^[6]

El refinamiento de Snell-Huygens

Snell propuso (y Huygens demostró) un límite más estricto que el de Arquímedes:

${\displaystyle n{\frac {3\sin {\frac {\pi }{n}}}{2+\cos {\frac {\pi }{n}}}}<\pi <n\left(2\sin {\frac {\pi }{3n}}+\tan {\frac {\pi }{3n}}\right).}$

Esto para n = 48 da una mejor aproximación (aproximadamente 3,14159292) que el método de Arquímedes para n = 768.

Derivación de las fórmulas de duplicación de Arquímedes

Círculo con triángulos semejantes: lado circunscrito, lado inscrito y complemento, lado inscrito partido y complemento

Sea un lado de un n- gono regular inscrito de longitud s _n y toque al círculo en los puntos A y B. Sea A′ el punto opuesto a A en el círculo, de modo que A′A es un diámetro y A′AB es un triángulo inscrito en un diámetro. Por el teorema de Tales , este es un triángulo rectángulo con ángulo recto en B. Sea c _n la longitud de A′B , que llamamos complemento de s _n ; por lo tanto c _n ² + s _n ²  = (2 r ) ² . Sea C bisectriz del arco de A a B, y sea C′ el punto opuesto a C en el círculo. Por lo tanto, la longitud de CA es s _{2 n} , la longitud de C′A es c _{2 n} y C′CA es en sí mismo un triángulo rectángulo de diámetro C′C. Como C biseca el arco de A a B, C′C biseca perpendicularmente la cuerda de A a B, digamos en P. El triángulo C′AP es, por tanto, un triángulo rectángulo y es semejante a C′CA, puesto que comparten el ángulo en C′. Por tanto, los tres lados correspondientes están en la misma proporción; en particular, tenemos C′A : C′C = C′P : C′A y AP : C′A = CA : C′C. El centro del círculo, O, biseca A′A, por lo que también tenemos el triángulo OAP semejante a A′AB, con OP con la mitad de la longitud de A′B. En términos de longitudes de los lados, esto nos da

${\displaystyle {\begin{aligned}c_{2n}^{2}&{}=\left(r+{\frac {1}{2}}c_{n}\right)2r\\c_{2n}&{}={\frac {s_{n}}{s_{2n}}}.\end{aligned}}}$

En la primera ecuación C′P es C′O+OP, longitud r + ¹ ⁄ ₂ c _n , y C′C es el diámetro, 2 r . Para un círculo unitario tenemos la famosa ecuación de duplicación de Ludolph van Ceulen ,

${\displaystyle c_{2n}={\sqrt {2+c_{n}}}.}$

Si ahora circunscribimos un n- gono regular, con el lado A″B″ paralelo a AB, entonces OAB y OA″B″ son triángulos semejantes, con A″B″ : AB = OC : OP. Llamemos al lado circunscrito S _n ; entonces esto es S _n  :  s _n  = 1 :  ¹ ⁄ ₂ c _n . (Hemos usado nuevamente que OP es la mitad de la longitud de A′B.) Así obtenemos

${\displaystyle c_{n}=2{\frac {s_{n}}{S_{n}}}.}$

Llamamos al perímetro inscrito u _n  = ns _n y al perímetro circunscrito U _n  = nS _n . Luego, combinando ecuaciones, tenemos

${\displaystyle c_{2n}={\frac {s_{n}}{s_{2n}}}=2{\frac {s_{2n}}{S_{2n}}},}$

de modo que

${\displaystyle u_{2n}^{2}=u_{n}U_{2n}.}$

Esto da una ecuación de media geométrica .

También podemos deducir

${\displaystyle 2{\frac {s_{2n}}{S_{2n}}}{\frac {s_{n}}{s_{2n}}}=2+2{\frac {s_{n}}{S_{n}}},}$

o

${\displaystyle {\frac {2}{U_{2n}}}={\frac {1}{u_{n}}}+{\frac {1}{U_{n}}}.}$

Esto da una ecuación de media armónica .

Aproximación de dardos

Integración de Monte Carlo del área del círculo unitario. La estimación a partir de estas 900 muestras es 4 ×709/900⁠  = 3,15111...

Cuando no se dispone de métodos más eficientes para encontrar áreas, podemos recurrir al método de “lanzar dardos”. Este método de Monte Carlo utiliza el hecho de que si se toman muestras aleatorias uniformemente esparcidas por la superficie de un cuadrado en el que se encuentra un disco, la proporción de muestras que impactan en el disco se aproxima a la relación entre el área del disco y el área del cuadrado. Este método debería considerarse un último recurso para calcular el área de un disco (o de cualquier forma), ya que requiere una enorme cantidad de muestras para obtener una precisión útil; una estimación buena de 10 ^{− n} requiere alrededor de 100 ⁿ muestras aleatorias (Thijssen 2006, p. 273).

Reordenamiento finito

Hemos visto que al dividir el disco en un número infinito de piezas podemos volver a ensamblar las piezas para formar un rectángulo. Un hecho notable descubierto hace relativamente poco tiempo (Laczkovich 1990) es que podemos diseccionar el disco en un número grande pero finito de piezas y luego volver a ensamblar las piezas para formar un cuadrado de igual área. Esto se llama el problema de la cuadratura del círculo de Tarski . La naturaleza de la prueba de Laczkovich es tal que prueba la existencia de tal partición (de hecho, de muchas particiones de este tipo) pero no exhibe ninguna partición en particular.

Círculos no euclidianos

Los círculos se pueden definir en geometría no euclidiana , y en particular en los planos hiperbólico y elíptico .

Por ejemplo, la esfera unitaria es un modelo para el plano elíptico bidimensional. Tiene una métrica intrínseca que surge al medir la longitud geodésica . Los círculos geodésicos son los paralelos en un sistema de coordenadas geodésicas . ${\displaystyle S^{2}(1)}$

Más precisamente, fijamos un punto que situamos en el cenit. Asociado a ese cenit hay un sistema de coordenadas polares geodésicas , , , donde z es el punto . En estas coordenadas, la distancia geodésica desde z a cualquier otro punto que tenga coordenadas es el valor de en x . Un círculo esférico es el conjunto de puntos a una distancia geodésica R del punto cenital z . De manera equivalente, con una incrustación fija en , el círculo esférico de radio centrado en z es el conjunto de x en tal que . ${\displaystyle \mathbf {z} \in S^{2}(1)}$ ${\displaystyle (\phi ,\theta )}$ ${\displaystyle 0\leq \phi \leq \pi }$ ${\displaystyle 0\leq \theta <2\pi }$ ${\displaystyle \phi =0}$ ${\displaystyle \mathbf {x} \in S^{2}(1)}$ ${\displaystyle (\phi ,\theta )}$ ${\displaystyle \phi }$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle R\leq \pi }$ ${\displaystyle S^{2}(1)}$ ${\displaystyle \mathbf {x} \cdot \mathbf {z} =\cos R}$

También podemos medir el área del disco esférico encerrado dentro de un círculo esférico, utilizando la medida del área de superficie intrínseca de la esfera. El área del disco de radio R se obtiene entonces mediante

${\displaystyle A=\int _{0}^{2\pi }\int _{0}^{R}\sin(\phi )d\phi \,d\theta =2\pi (1-\cos R).}$

De manera más general, si una esfera tiene un radio de curvatura , entonces el área del disco de radio R está dada por ${\displaystyle S^{2}(\rho )}$ ${\displaystyle \rho }$

${\displaystyle A=2\pi \rho ^{2}(1-\cos(R/\rho )).}$

Obsérvese que, como aplicación de la regla de L'Hôpital , esto tiende al área euclidiana en el límite plano . ${\displaystyle \pi R^{2}}$ ${\displaystyle \rho \to \infty }$

El caso hiperbólico es similar, con el área de un disco de radio intrínseco R en el plano hiperbólico (curvatura constante) dada por ${\displaystyle -1}$

${\displaystyle A=2\pi (1-\cosh R)}$

donde cosh es el coseno hiperbólico . De manera más general, para el plano hiperbólico de curvatura constante, la respuesta es ${\displaystyle -k}$

${\displaystyle A=2\pi k^{-2}(1-\cosh(kR)).}$

Estas identidades son importantes para las desigualdades de comparación en geometría. Por ejemplo, el área encerrada por un círculo de radio R en un espacio plano siempre es mayor que el área de un círculo esférico y menor que la de un círculo hiperbólico, siempre que los tres círculos tengan el mismo radio (intrínseco). Es decir,

${\displaystyle 2\pi (1-\cos R)<\pi R^{2}<2\pi (1-\cosh R)}$

para todos . Intuitivamente, esto se debe a que la esfera tiende a curvarse sobre sí misma, dando lugar a círculos de área más pequeña que los del plano, mientras que el plano hiperbólico, cuando se sumerge en el espacio, desarrolla franjas que producen área adicional. Es más generalmente cierto que el área del círculo de un radio fijo R es una función estrictamente decreciente de la curvatura. ${\displaystyle R>0}$

En todos los casos, si es la curvatura (constante, positiva o negativa), entonces la desigualdad isoperimétrica para un dominio con área A y perímetro L es ${\displaystyle k}$

${\displaystyle L^{2}\geq 4\pi A-kA^{2}}$

donde la igualdad se logra precisamente para el círculo. ^[7]

Generalizaciones

Podemos estirar un disco para formar una elipse . Debido a que este estiramiento es una transformación lineal del plano, tiene un factor de distorsión que cambiará el área pero conservará las proporciones de las áreas. Esta observación se puede utilizar para calcular el área de una elipse arbitraria a partir del área de un círculo unitario.

Considere el círculo unitario circunscrito por un cuadrado de lado 2. La transformación convierte el círculo en una elipse estirando o encogiendo los diámetros horizontal y vertical de los ejes mayor y menor de la elipse. El cuadrado se convierte en un rectángulo que circunscribe la elipse. La relación entre el área del círculo y el cuadrado es π /4, lo que significa que la relación entre la elipse y el rectángulo también es π /4. Suponga que a y b son las longitudes de los ejes mayor y menor de la elipse. Como el área del rectángulo es ab , el área de la elipse es π ab /4.

También podemos considerar mediciones análogas en dimensiones superiores. Por ejemplo, podemos querer encontrar el volumen dentro de una esfera. Cuando tenemos una fórmula para el área de la superficie, podemos usar el mismo tipo de enfoque de "cebolla" que usamos para el disco.

Véase también

• Radio equivalente al área
• Área de un triángulo

Referencias

1. Stewart, James (2003). Cálculo de una variable: trascendentales tempranos (5.ª ed.). Toronto, Ontario: Brook/Cole. pp. 3. ISBN 0-534-39330-6Sin embargo , mediante un razonamiento indirecto, Eudoxo (siglo V a. C.) utilizó el método exhaustivo para demostrar la conocida fórmula del área de un disco: ${\displaystyle A=\pi r^{2}.}$
2. Heath, Thomas L. (2003), Un manual de matemáticas griegas, Courier Dover Publications, págs. 121-132, ISBN 0-486-43231-9.
3. Hill, George. Lecciones de geometría: para uso de principiantes , página 124 (1894).
4. Clegg, Brian (2012). Introducción al infinito . Icon Books. pág. 69. ISBN 978-1-84831-406-1.
5. Martzloff, Jean-Claude (2006). Una historia de las matemáticas chinas . Springer. pág. 281. ISBN. 9783540337829.
6. No todas las mejores aproximaciones racionales son convergentes de la fracción continua!
7. Isaac Chavel (2001), Desigualdades isoperimétricas , Cambridge University Press

Bibliografía

• Arquímedes (1897), "Medición de un círculo", en Heath, TL (ed.), The Works of Archimedes, Cambridge University Press
  (Publicado originalmente por Cambridge University Press , 1897, basado en la versión griega de JL Heiberg).
• Beckmann, Petr (1976), Una historia de Pi , St. Martin's Griffin , ISBN 978-0-312-38185-1
• Gerretsen, J.; Verdenduin, P. (1983), "Capítulo 8: Polígonos y poliedros", en H. Behnke; F. Bachmann; K. Fladt; H. Kunle (eds.), Fundamentals of Mathematics, Volumen II: Geometry , traducido por SH Gould, MIT Press , págs. 243–250, ISBN 978-0-262-52094-2
  (Originalmente Grundzüge der Mathematik , Vandenhoeck & Ruprecht, Göttingen, 1971.)
• Laczkovich, Miklós (1990), "Equidecomposabilidad y discrepancia: una solución al problema de la cuadratura del círculo de Tarski", Journal für die reine und angewandte Mathematik , 1990 (404): 77–117, doi :10.1515/crll.1990.404.77, MR  1037431 , S2CID  117762563
• Lang, Serge (1985), "La longitud del círculo", Math! : Encuentros con estudiantes de secundaria , Springer-Verlag , ISBN 978-0-387-96129-3
• Smith, David Eugene ; Mikami, Yoshio (1914), Una historia de las matemáticas japonesas, Chicago: Open Court Publishing , págs. 130–132, ISBN 978-0-87548-170-8
• Thijssen, JM (2006), Física computacional , Cambridge University Press, pág. 273, ISBN 978-0-521-57588-1

Enlaces externos

• Noticias científicas sobre el problema de Tarski Archivado el 13 de abril de 2008 en Wayback Machine