Técnica de evaluación integral
En matemáticas , una sustitución trigonométrica reemplaza una función trigonométrica por otra expresión. En cálculo , las sustituciones trigonométricas son una técnica para evaluar integrales. En este caso, una expresión que involucra una función radical se reemplaza por una trigonométrica. Las identidades trigonométricas pueden ayudar a simplificar la respuesta. [1] [2] Al igual que otros métodos de integración por sustitución, al evaluar una integral definida, puede ser más simple deducir completamente la antiderivada antes de aplicar los límites de integración.
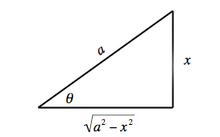
Caso I: Integrandos que contienena2−incógnita2 Dejar y utilizar la identidad x = a sin θ , {\displaystyle x=a\sin \theta ,} 1 − sin 2 θ = cos 2 θ . {\displaystyle 1-\sin ^{2}\theta =\cos ^{2}\theta .}
Ejemplos del caso I Construcción geométrica para el caso I
Ejemplo 1 En la integral
∫ d x a 2 − x 2 , {\displaystyle \int {\frac {dx}{\sqrt {a^{2}-x^{2}}}},}
podemos usar
x = a sin θ , d x = a cos θ d θ , θ = arcsin x a . {\displaystyle x=a\sin \theta ,\quad dx=a\cos \theta \,d\theta ,\quad \theta =\arcsin {\frac {x}{a}}.}
Entonces, ∫ d x a 2 − x 2 = ∫ a cos θ d θ a 2 − a 2 sin 2 θ = ∫ a cos θ d θ a 2 ( 1 − sin 2 θ ) = ∫ a cos θ d θ a 2 cos 2 θ = ∫ d θ = θ + C = arcsin x a + C . {\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}}\\[6pt]&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}(1-\sin ^{2}\theta )}}}\\[6pt]&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\\[6pt]&=\int d\theta \\[6pt]&=\theta +C\\[6pt]&=\arcsin {\frac {x}{a}}+C.\end{aligned}}}
El paso anterior requiere que y podamos elegir ser la raíz principal de e imponer la restricción utilizando la función seno inverso. a > 0 {\displaystyle a>0} cos θ > 0. {\displaystyle \cos \theta >0.} a {\displaystyle a} a 2 , {\displaystyle a^{2},} − π / 2 < θ < π / 2 {\displaystyle -\pi /2<\theta <\pi /2}
Para una integral definida, se debe determinar cómo cambian los límites de integración. Por ejemplo, como va de a entonces va de a entonces va de a Entonces, x {\displaystyle x} 0 {\displaystyle 0} a / 2 , {\displaystyle a/2,} sin θ {\displaystyle \sin \theta } 0 {\displaystyle 0} 1 / 2 , {\displaystyle 1/2,} θ {\displaystyle \theta } 0 {\displaystyle 0} π / 6. {\displaystyle \pi /6.}
∫ 0 a / 2 d x a 2 − x 2 = ∫ 0 π / 6 d θ = π 6 . {\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\int _{0}^{\pi /6}d\theta ={\frac {\pi }{6}}.}
Se debe tener cuidado al elegir los límites. Debido a que la integración anterior requiere que , solo pueda ir de a Ignorando esta restricción, se podría haber elegido ir de a lo que habría dado como resultado el valor negativo del valor real. − π / 2 < θ < π / 2 {\displaystyle -\pi /2<\theta <\pi /2} θ {\displaystyle \theta } 0 {\displaystyle 0} π / 6. {\displaystyle \pi /6.} θ {\displaystyle \theta } π {\displaystyle \pi } 5 π / 6 , {\displaystyle 5\pi /6,}
Alternativamente, evalúe completamente las integrales indefinidas antes de aplicar las condiciones de contorno. En ese caso, la antiderivada da
∫ 0 a / 2 d x a 2 − x 2 = arcsin ( x a ) | 0 a / 2 = arcsin ( 1 2 ) − arcsin ( 0 ) = π 6 {\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\arcsin \left({\frac {x}{a}}\right){\Biggl |}_{0}^{a/2}=\arcsin \left({\frac {1}{2}}\right)-\arcsin(0)={\frac {\pi }{6}}}
Ejemplo 2 La integral
∫ a 2 − x 2 d x , {\displaystyle \int {\sqrt {a^{2}-x^{2}}}\,dx,}
puede evaluarse dejando donde de modo que y por el rango del arcoseno, de modo que y x = a sin θ , d x = a cos θ d θ , θ = arcsin x a , {\textstyle x=a\sin \theta ,\,dx=a\cos \theta \,d\theta ,\,\theta =\arcsin {\dfrac {x}{a}},} a > 0 {\displaystyle a>0} a 2 = a , {\textstyle {\sqrt {a^{2}}}=a,} − π / 2 ≤ θ ≤ π / 2 {\textstyle -\pi /2\leq \theta \leq \pi /2} cos θ ≥ 0 {\displaystyle \cos \theta \geq 0} cos 2 θ = cos θ . {\textstyle {\sqrt {\cos ^{2}\theta }}=\cos \theta .}
Entonces, ∫ a 2 − x 2 d x = ∫ a 2 − a 2 sin 2 θ ( a cos θ ) d θ = ∫ a 2 ( 1 − sin 2 θ ) ( a cos θ ) d θ = ∫ a 2 ( cos 2 θ ) ( a cos θ ) d θ = ∫ ( a cos θ ) ( a cos θ ) d θ = a 2 ∫ cos 2 θ d θ = a 2 ∫ ( 1 + cos 2 θ 2 ) d θ = a 2 2 ( θ + 1 2 sin 2 θ ) + C = a 2 2 ( θ + sin θ cos θ ) + C = a 2 2 ( arcsin x a + x a 1 − x 2 a 2 ) + C = a 2 2 arcsin x a + x 2 a 2 − x 2 + C . {\displaystyle {\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1-\sin ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\[6pt]&=a^{2}\int \cos ^{2}\theta \,d\theta \\[6pt]&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\sin 2\theta \right)+C\\[6pt]&={\frac {a^{2}}{2}}(\theta +\sin \theta \cos \theta )+C\\[6pt]&={\frac {a^{2}}{2}}\left(\arcsin {\frac {x}{a}}+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\[6pt]&={\frac {a^{2}}{2}}\arcsin {\frac {x}{a}}+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C.\end{aligned}}}
Para una integral definida, los límites cambian una vez que se realiza la sustitución y se determinan utilizando la ecuación con valores en el rango . Alternativamente, aplique los términos de límite directamente a la fórmula para la antiderivada. θ = arcsin x a , {\textstyle \theta =\arcsin {\dfrac {x}{a}},} − π / 2 ≤ θ ≤ π / 2. {\textstyle -\pi /2\leq \theta \leq \pi /2.}
Por ejemplo, la integral definida
∫ − 1 1 4 − x 2 d x , {\displaystyle \int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx,}
puede evaluarse sustituyendo con los límites determinados usando x = 2 sin θ , d x = 2 cos θ d θ , {\displaystyle x=2\sin \theta ,\,dx=2\cos \theta \,d\theta ,} θ = arcsin x 2 . {\textstyle \theta =\arcsin {\dfrac {x}{2}}.}
Porque y arcsin ( 1 / 2 ) = π / 6 {\displaystyle \arcsin(1/{2})=\pi /6} arcsin ( − 1 / 2 ) = − π / 6 , {\displaystyle \arcsin(-1/2)=-\pi /6,} ∫ − 1 1 4 − x 2 d x = ∫ − π / 6 π / 6 4 − 4 sin 2 θ ( 2 cos θ ) d θ = ∫ − π / 6 π / 6 4 ( 1 − sin 2 θ ) ( 2 cos θ ) d θ = ∫ − π / 6 π / 6 4 ( cos 2 θ ) ( 2 cos θ ) d θ = ∫ − π / 6 π / 6 ( 2 cos θ ) ( 2 cos θ ) d θ = 4 ∫ − π / 6 π / 6 cos 2 θ d θ = 4 ∫ − π / 6 π / 6 ( 1 + cos 2 θ 2 ) d θ = 2 [ θ + 1 2 sin 2 θ ] − π / 6 π / 6 = [ 2 θ + sin 2 θ ] | − π / 6 π / 6 = ( π 3 + sin π 3 ) − ( − π 3 + sin ( − π 3 ) ) = 2 π 3 + 3 . {\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\sin ^{2}\theta }}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\sin ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&=2\left[\theta +{\frac {1}{2}}\sin 2\theta \right]_{-\pi /6}^{\pi /6}=[2\theta +\sin 2\theta ]{\Biggl |}_{-\pi /6}^{\pi /6}\\[6pt]&=\left({\frac {\pi }{3}}+\sin {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\sin \left(-{\frac {\pi }{3}}\right)\right)={\frac {2\pi }{3}}+{\sqrt {3}}.\end{aligned}}}
Por otra parte, la aplicación directa de los términos de contorno a la fórmula previamente obtenida para la antiderivada da como resultado
lo anterior. ∫ − 1 1 4 − x 2 d x = [ 2 2 2 arcsin x 2 + x 2 2 2 − x 2 ] − 1 1 = ( 2 arcsin 1 2 + 1 2 4 − 1 ) − ( 2 arcsin ( − 1 2 ) + − 1 2 4 − 1 ) = ( 2 ⋅ π 6 + 3 2 ) − ( 2 ⋅ ( − π 6 ) − 3 2 ) = 2 π 3 + 3 {\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left[{\frac {2^{2}}{2}}\arcsin {\frac {x}{2}}+{\frac {x}{2}}{\sqrt {2^{2}-x^{2}}}\right]_{-1}^{1}\\[6pt]&=\left(2\arcsin {\frac {1}{2}}+{\frac {1}{2}}{\sqrt {4-1}}\right)-\left(2\arcsin \left(-{\frac {1}{2}}\right)+{\frac {-1}{2}}{\sqrt {4-1}}\right)\\[6pt]&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}
Caso II: Integrandos que contienena2+incógnita2 Dejar y utilizar la identidad x = a tan θ , {\displaystyle x=a\tan \theta ,} 1 + tan 2 θ = sec 2 θ . {\displaystyle 1+\tan ^{2}\theta =\sec ^{2}\theta .}
Ejemplos del caso II Construcción geométrica para el caso II
Ejemplo 1 En la integral
∫ d x a 2 + x 2 {\displaystyle \int {\frac {dx}{a^{2}+x^{2}}}}
podemos escribir
x = a tan θ , d x = a sec 2 θ d θ , θ = arctan x a , {\displaystyle x=a\tan \theta ,\quad dx=a\sec ^{2}\theta \,d\theta ,\quad \theta =\arctan {\frac {x}{a}},}
de modo que la integral se convierte en
∫ d x a 2 + x 2 = ∫ a sec 2 θ d θ a 2 + a 2 tan 2 θ = ∫ a sec 2 θ d θ a 2 ( 1 + tan 2 θ ) = ∫ a sec 2 θ d θ a 2 sec 2 θ = ∫ d θ a = θ a + C = 1 a arctan x a + C , {\displaystyle {\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\\[6pt]&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}(1+\tan ^{2}\theta )}}\\[6pt]&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}\sec ^{2}\theta }}\\[6pt]&=\int {\frac {d\theta }{a}}\\[6pt]&={\frac {\theta }{a}}+C\\[6pt]&={\frac {1}{a}}\arctan {\frac {x}{a}}+C,\end{aligned}}}
proporcionó a ≠ 0. {\displaystyle a\neq 0.}
Para una integral definida, los límites cambian una vez que se realiza la sustitución y se determinan utilizando la ecuación con valores en el rango . Alternativamente, aplique los términos de límite directamente a la fórmula para la antiderivada. θ = arctan x a , {\displaystyle \theta =\arctan {\frac {x}{a}},} − π 2 < θ < π 2 . {\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}.}
Por ejemplo, la integral definida
∫ 0 1 4 d x 1 + x 2 {\displaystyle \int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,}
puede evaluarse sustituyendo con los límites determinados usando x = tan θ , d x = sec 2 θ d θ , {\displaystyle x=\tan \theta ,\,dx=\sec ^{2}\theta \,d\theta ,} θ = arctan x . {\displaystyle \theta =\arctan x.}
Desde y arctan 0 = 0 {\displaystyle \arctan 0=0} arctan 1 = π / 4 , {\displaystyle \arctan 1=\pi /4,} ∫ 0 1 4 d x 1 + x 2 = 4 ∫ 0 1 d x 1 + x 2 = 4 ∫ 0 π / 4 sec 2 θ d θ 1 + tan 2 θ = 4 ∫ 0 π / 4 sec 2 θ d θ sec 2 θ = 4 ∫ 0 π / 4 d θ = ( 4 θ ) | 0 π / 4 = 4 ( π 4 − 0 ) = π . {\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{1+\tan ^{2}\theta }}\\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{\sec ^{2}\theta }}\\[6pt]&=4\int _{0}^{\pi /4}d\theta \\[6pt]&=(4\theta ){\Bigg |}_{0}^{\pi /4}=4\left({\frac {\pi }{4}}-0\right)=\pi .\end{aligned}}}
Mientras tanto, la aplicación directa de los términos de contorno a la fórmula para la antiderivada produce
el mismo resultado que antes. ∫ 0 1 4 d x 1 + x 2 = 4 ∫ 0 1 d x 1 + x 2 = 4 [ 1 1 arctan x 1 ] 0 1 = 4 ( arctan x ) | 0 1 = 4 ( arctan 1 − arctan 0 ) = 4 ( π 4 − 0 ) = π , {\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\[6pt]&=4\left[{\frac {1}{1}}\arctan {\frac {x}{1}}\right]_{0}^{1}\\[6pt]&=4(\arctan x){\Bigg |}_{0}^{1}\\[6pt]&=4(\arctan 1-\arctan 0)\\[6pt]&=4\left({\frac {\pi }{4}}-0\right)=\pi ,\end{aligned}}}
Ejemplo 2 La integral
∫ a 2 + x 2 d x {\displaystyle \int {\sqrt {a^{2}+x^{2}}}\,{dx}}
puede evaluarse dejando x = a tan θ , d x = a sec 2 θ d θ , θ = arctan x a , {\displaystyle x=a\tan \theta ,\,dx=a\sec ^{2}\theta \,d\theta ,\,\theta =\arctan {\frac {x}{a}},}
donde de modo que y por el rango de arcotangente, de modo que y a > 0 {\displaystyle a>0} a 2 = a , {\displaystyle {\sqrt {a^{2}}}=a,} − π 2 < θ < π 2 {\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}} sec θ > 0 {\displaystyle \sec \theta >0} sec 2 θ = sec θ . {\displaystyle {\sqrt {\sec ^{2}\theta }}=\sec \theta .}
Entonces,
la integral de la secante al cubo se puede evaluar mediante integración por partes . Como resultado, ∫ a 2 + x 2 d x = ∫ a 2 + a 2 tan 2 θ ( a sec 2 θ ) d θ = ∫ a 2 ( 1 + tan 2 θ ) ( a sec 2 θ ) d θ = ∫ a 2 sec 2 θ ( a sec 2 θ ) d θ = ∫ ( a sec θ ) ( a sec 2 θ ) d θ = a 2 ∫ sec 3 θ d θ . {\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\[6pt]&=a^{2}\int \sec ^{3}\theta \,d\theta .\\[6pt]\end{aligned}}} ∫ a 2 + x 2 d x = a 2 2 ( sec θ tan θ + ln | sec θ + tan θ | ) + C = a 2 2 ( 1 + x 2 a 2 ⋅ x a + ln | 1 + x 2 a 2 + x a | ) + C = 1 2 ( x a 2 + x 2 + a 2 ln | x + a 2 + x 2 a | ) + C . {\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|{\frac {x+{\sqrt {a^{2}+x^{2}}}}{a}}\right|\right)+C.\end{aligned}}}
Caso III: Integrandos que contienenincógnita2−a2 Dejar y utilizar la identidad x = a sec θ , {\displaystyle x=a\sec \theta ,} sec 2 θ − 1 = tan 2 θ . {\displaystyle \sec ^{2}\theta -1=\tan ^{2}\theta .}
Ejemplos del Caso III Construcción geométrica para el caso III Integrales como
∫ d x x 2 − a 2 {\displaystyle \int {\frac {dx}{x^{2}-a^{2}}}}
También se puede evaluar mediante fracciones parciales en lugar de sustituciones trigonométricas. Sin embargo, la integral
∫ x 2 − a 2 d x {\displaystyle \int {\sqrt {x^{2}-a^{2}}}\,dx}
No puede. En este caso, una sustitución adecuada es: x = a sec θ , d x = a sec θ tan θ d θ , θ = arcsec x a , {\displaystyle x=a\sec \theta ,\,dx=a\sec \theta \tan \theta \,d\theta ,\,\theta =\operatorname {arcsec} {\frac {x}{a}},}
donde de modo que y suponiendo de modo que y a > 0 {\displaystyle a>0} a 2 = a , {\displaystyle {\sqrt {a^{2}}}=a,} 0 ≤ θ < π 2 {\displaystyle 0\leq \theta <{\frac {\pi }{2}}} x > 0 , {\displaystyle x>0,} tan θ ≥ 0 {\displaystyle \tan \theta \geq 0} tan 2 θ = tan θ . {\displaystyle {\sqrt {\tan ^{2}\theta }}=\tan \theta .}
Entonces, ∫ x 2 − a 2 d x = ∫ a 2 sec 2 θ − a 2 ⋅ a sec θ tan θ d θ = ∫ a 2 ( sec 2 θ − 1 ) ⋅ a sec θ tan θ d θ = ∫ a 2 tan 2 θ ⋅ a sec θ tan θ d θ = ∫ a 2 sec θ tan 2 θ d θ = a 2 ∫ ( sec θ ) ( sec 2 θ − 1 ) d θ = a 2 ∫ ( sec 3 θ − sec θ ) d θ . {\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&=\int {\sqrt {a^{2}\sec ^{2}\theta -a^{2}}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}(\sec ^{2}\theta -1)}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}\tan ^{2}\theta }}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int a^{2}\sec \theta \tan ^{2}\theta \,d\theta \\&=a^{2}\int (\sec \theta )(\sec ^{2}\theta -1)\,d\theta \\&=a^{2}\int (\sec ^{3}\theta -\sec \theta )\,d\theta .\end{aligned}}}
Se puede evaluar la integral de la función secante multiplicando el numerador y el denominador por y la integral de la secante al cubo por partes. [3] Como resultado, ( sec θ + tan θ ) {\displaystyle (\sec \theta +\tan \theta )} ∫ x 2 − a 2 d x = a 2 2 ( sec θ tan θ + ln | sec θ + tan θ | ) − a 2 ln | sec θ + tan θ | + C = a 2 2 ( sec θ tan θ − ln | sec θ + tan θ | ) + C = a 2 2 ( x a ⋅ x 2 a 2 − 1 − ln | x a + x 2 a 2 − 1 | ) + C = 1 2 ( x x 2 − a 2 − a 2 ln | x + x 2 − a 2 a | ) + C . {\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\[6pt]&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}}
Cuando lo cual sucede cuando se da el rango de arcosecante, es decir en cambio en ese caso. π 2 < θ ≤ π , {\displaystyle {\frac {\pi }{2}}<\theta \leq \pi ,} x < 0 {\displaystyle x<0} tan θ ≤ 0 , {\displaystyle \tan \theta \leq 0,} tan 2 θ = − tan θ {\displaystyle {\sqrt {\tan ^{2}\theta }}=-\tan \theta }
Sustituciones que eliminan funciones trigonométricas La sustitución se puede utilizar para eliminar funciones trigonométricas.
Por ejemplo,
∫ f ( sin ( x ) , cos ( x ) ) d x = ∫ 1 ± 1 − u 2 f ( u , ± 1 − u 2 ) d u u = sin ( x ) ∫ f ( sin ( x ) , cos ( x ) ) d x = ∫ 1 ∓ 1 − u 2 f ( ± 1 − u 2 , u ) d u u = cos ( x ) ∫ f ( sin ( x ) , cos ( x ) ) d x = ∫ 2 1 + u 2 f ( 2 u 1 + u 2 , 1 − u 2 1 + u 2 ) d u u = tan ( x 2 ) {\displaystyle {\begin{aligned}\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\sin(x)\\[6pt]\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\[6pt]\int f(\sin(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\frac {x}{2}}\right)\\[6pt]\end{aligned}}}
La última sustitución se conoce como sustitución de Weierstrass , que utiliza fórmulas de semiángulo tangente .
Por ejemplo,
∫ 4 cos x ( 1 + cos x ) 3 d x = ∫ 2 1 + u 2 4 ( 1 − u 2 1 + u 2 ) ( 1 + 1 − u 2 1 + u 2 ) 3 d u = ∫ ( 1 − u 2 ) ( 1 + u 2 ) d u = ∫ ( 1 − u 4 ) d u = u − u 5 5 + C = tan x 2 − 1 5 tan 5 x 2 + C . {\displaystyle {\begin{aligned}\int {\frac {4\cos x}{(1+\cos x)^{3}}}\,dx&=\int {\frac {2}{1+u^{2}}}{\frac {4\left({\frac {1-u^{2}}{1+u^{2}}}\right)}{\left(1+{\frac {1-u^{2}}{1+u^{2}}}\right)^{3}}}\,du=\int (1-u^{2})(1+u^{2})\,du\\&=\int (1-u^{4})\,du=u-{\frac {u^{5}}{5}}+C=\tan {\frac {x}{2}}-{\frac {1}{5}}\tan ^{5}{\frac {x}{2}}+C.\end{aligned}}}
Sustitución hiperbólica También se pueden utilizar sustituciones de funciones hiperbólicas para simplificar integrales. [4]
Por ejemplo, para integrar , introduzca la sustitución (y por lo tanto ), luego use la identidad para encontrar: 1 / a 2 + x 2 {\displaystyle 1/{\sqrt {a^{2}+x^{2}}}} x = a sinh u {\displaystyle x=a\sinh {u}} d x = a cosh u d u {\displaystyle dx=a\cosh u\,du} cosh 2 ( x ) − sinh 2 ( x ) = 1 {\displaystyle \cosh ^{2}(x)-\sinh ^{2}(x)=1}
∫ d x a 2 + x 2 = ∫ a cosh u d u a 2 + a 2 sinh 2 u = ∫ cosh u d u 1 + sinh 2 u = ∫ cosh u cosh u d u = u + C = sinh − 1 x a + C . {\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}+x^{2}}}}&=\int {\frac {a\cosh u\,du}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\\[6pt]&=\int {\frac {\cosh {u}\,du}{\sqrt {1+\sinh ^{2}{u}}}}\\[6pt]&=\int {\frac {\cosh {u}}{\cosh u}}\,du\\[6pt]&=u+C\\[6pt]&=\sinh ^{-1}{\frac {x}{a}}+C.\end{aligned}}}
Si se desea, este resultado se puede transformar aún más utilizando otras identidades, como por ejemplo utilizando la relación sinh − 1 z = arsinh z = ln ( z + z 2 + 1 ) {\displaystyle \sinh ^{-1}{z}=\operatorname {arsinh} {z}=\ln(z+{\sqrt {z^{2}+1}})} : sinh − 1 x a + C = ln ( x a + x 2 a 2 + 1 ) + C = ln ( x + x 2 + a 2 a ) + C . {\displaystyle {\begin{aligned}\sinh ^{-1}{\frac {x}{a}}+C&=\ln \left({\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}+1}}\,\right)+C\\[6pt]&=\ln \left({\frac {x+{\sqrt {x^{2}+a^{2}}}}{a}}\,\right)+C.\end{aligned}}}
Véase también Wikiversidad tiene recursos de aprendizaje sobre sustituciones trigonométricas
Wikilibros tiene un libro sobre el tema: Cálculo/Técnicas de integración/Sustitución trigonométrica
Referencias