Efecto mariposa

Idea de que pequeñas causas pueden tener grandes efectos

Un gráfico del atractor extraño de Lorenz para valores ρ=28, σ = 10, β = 8/3. El efecto mariposa o dependencia sensible de las condiciones iniciales es propiedad de un sistema dinámico que, a partir de cualquiera de varias condiciones iniciales alternativas arbitrariamente cercanas en el atractor, los puntos iterados se dispersarán arbitrariamente entre sí.

Demostración experimental del efecto mariposa con seis grabaciones del mismo doble péndulo . En cada grabación, el péndulo parte casi con la misma condición inicial. Con el tiempo, las diferencias en la dinámica pasan de ser casi imperceptibles a ser drásticas.

En la teoría del caos , el efecto mariposa es la dependencia sensible de las condiciones iniciales en la que un pequeño cambio en un estado de un sistema no lineal determinista puede resultar en grandes diferencias en un estado posterior.

El término está estrechamente asociado con el trabajo del matemático y meteorólogo Edward Norton Lorenz . Señaló que el efecto mariposa se deriva del ejemplo metafórico de los detalles de un tornado (el momento exacto de su formación, el camino exacto tomado) siendo influenciados por perturbaciones menores, como una mariposa distante batiendo sus alas varias semanas antes. Lorenz originalmente usó una gaviota que causaba una tormenta, pero en 1972 lo persuadieron para que la hiciera más poética con el uso de una mariposa y un tornado. ^{[1] [2]} Descubrió el efecto cuando observó ejecuciones de su modelo meteorológico con datos de condiciones iniciales que fueron redondeados de una manera aparentemente intrascendente. Observó que el modelo meteorológico no lograría reproducir los resultados de las ejecuciones con datos de condición inicial no redondeados. Un cambio muy pequeño en las condiciones iniciales había creado un resultado significativamente diferente. ^[3]

La idea de que pequeñas causas pueden tener grandes efectos en el tiempo fue reconocida anteriormente por el matemático y físico francés Henri Poincaré . El matemático y filósofo estadounidense Norbert Wiener también contribuyó a esta teoría. El trabajo de Lorenz colocó el concepto de inestabilidad de la atmósfera terrestre en una base cuantitativa y vinculó el concepto de inestabilidad a las propiedades de grandes clases de sistemas dinámicos que están experimentando dinámicas no lineales y caos determinista . ^[4]

Desde entonces, el concepto del efecto mariposa se ha utilizado fuera del contexto de la ciencia meteorológica como un término amplio para cualquier situación en la que se supone que un pequeño cambio es la causa de consecuencias mayores.

Historia

En La vocación del hombre (1800), Johann Gottlieb Fichte dice "no se puede quitar un solo grano de arena de su lugar sin por ello... cambiar algo en todas las partes del todo inconmensurable".

La teoría del caos y la dependencia sensible de las condiciones iniciales se describieron en numerosas formas de literatura. Esto se evidencia en el caso del problema de los tres cuerpos planteado por Poincaré en 1890. ^[5] Más tarde propuso que tales fenómenos podrían ser comunes, por ejemplo, en meteorología. ^[6]

En 1898, Jacques Hadamard observó una divergencia general de trayectorias en espacios de curvatura negativa. Pierre Duhem discutió el posible significado general de esto en 1908. ^[5]

En 1950, Alan Turing señaló: "El desplazamiento de un solo electrón en una milmillonésima de centímetro en un momento dado podría marcar la diferencia entre que un hombre muera por una avalancha un año después o escapar". ^[7]

La idea de que la muerte de una mariposa podría eventualmente tener un efecto dominó de gran alcance en eventos históricos posteriores hizo su primera aparición conocida en " A Sound of Thunder ", un cuento de 1952 de Ray Bradbury . "A Sound of Thunder" presenta viajes en el tiempo. ^[8]

Más precisamente, sin embargo, casi la idea exacta y la frase exacta —el ala de un pequeño insecto que afecta a los vientos de toda la atmósfera— se publicó en un libro para niños que alcanzó gran éxito y fue mundialmente conocido en 1962, un año antes de que Lorenz publicara:

"... cualquier cosa que hagamos afecta a todo y a todos los demás, aunque sea en la forma más pequeña. Vaya, cuando una mosca doméstica bate sus alas, una brisa recorre el mundo".

-- La Princesa de la Razón Pura

—  Norton Juster, La cabina de peaje fantasma

En 1961, Lorenz estaba ejecutando un modelo numérico por computadora para rehacer una predicción meteorológica a partir de la mitad de la ejecución anterior como atajo. Ingresó la condición inicial 0.506 de la impresión en lugar de ingresar el valor de precisión total 0.506127. El resultado fue un escenario meteorológico completamente diferente. ^[9]

Lorenz escribió:

En un momento decidí repetir algunos de los cálculos para examinar lo que estaba sucediendo con mayor detalle. Detuve la computadora, escribí una línea de números que había impreso un rato antes y la puse en funcionamiento nuevamente. Fui al pasillo a tomar una taza de café y regresé después de aproximadamente una hora, tiempo durante el cual la computadora había simulado aproximadamente dos meses de clima. Los números que se imprimían no se parecían en nada a los antiguos. Inmediatamente sospeché que un tubo de vacío estaba débil o algún otro problema con la computadora, lo cual no era infrecuente, pero antes de llamar al servicio técnico decidí ver dónde había ocurrido el error, sabiendo que esto podría acelerar el proceso de servicio. En lugar de una ruptura repentina, descubrí que los nuevos valores al principio repetían los antiguos, pero poco después diferían en una y luego en varias unidades en el último lugar [decimal], y luego comenzaron a diferir en el penúltimo lugar y luego en el lugar anterior a eso. De hecho, las diferencias duplicaron su tamaño de manera más o menos constante aproximadamente cada cuatro días, hasta que toda semejanza con la producción original desapareció en algún momento del segundo mes. Esto fue suficiente para decirme lo que había sucedido: los números que había escrito no eran los números originales exactos, sino los valores redondeados que habían aparecido en la impresión original. Los errores de redondeo iniciales fueron los culpables; se fueron amplificando constantemente hasta dominar la solución.

—  EN Lorenz, La esencia del caos , U. Washington Press, Seattle (1993), página 134 ^[10]

En 1963, Lorenz publicó un estudio teórico de este efecto en un artículo fundamental muy citado llamado Deterministic Nonperiodic Flow ^{[3] [11]} (los cálculos se realizaron en una computadora Royal McBee LGP-30 ). ^{[12] [13]} En otra parte declaró:

Un meteorólogo comentó que si la teoría fuera correcta, un aleteo de una gaviota sería suficiente para alterar el curso del tiempo para siempre. La controversia aún no se ha resuelto, pero las evidencias más recientes parecen favorecer a las gaviotas. ^[13]

Siguiendo las propuestas de sus colegas, en discursos y artículos posteriores, Lorenz utilizó la mariposa más poética . Según Lorenz, cuando no pudo proporcionar un título para una charla que iba a presentar en la 139ª reunión de la Asociación Americana para el Avance de la Ciencia en 1972, Philip Merilees inventó ¿El aleteo de una mariposa en Brasil provoca un tornado? ¿en Texas? como título. ^[1] Aunque una mariposa batiendo sus alas se ha mantenido constante en la expresión de este concepto, la ubicación de la mariposa, las consecuencias y la ubicación de las consecuencias han variado ampliamente. ^[14]

La frase se refiere a la idea de que las alas de una mariposa pueden crear pequeños cambios en la atmósfera que, en última instancia, pueden alterar la trayectoria de un tornado o retrasar, acelerar o incluso prevenir la aparición de un tornado en otro lugar. La mariposa no impulsa ni crea directamente el tornado, pero el término pretende implicar que el aleteo de las alas de la mariposa puede causar el tornado: en el sentido de que el aleteo de las alas es parte de las condiciones iniciales de un complejo interconectado. web; un conjunto de condiciones conduce a un tornado, mientras que el otro conjunto de condiciones no. El aleteo representa un pequeño cambio en la condición inicial del sistema, que se convierte en cascada en alteraciones de eventos a gran escala (compárese: efecto dominó ). Si la mariposa no hubiera batido sus alas, la trayectoria del sistema podría haber sido muy diferente, pero también es igualmente posible que el conjunto de condiciones sin que la mariposa batiera sus alas sea el conjunto que conduzca a un tornado.

El efecto mariposa presenta un desafío obvio para la predicción, ya que las condiciones iniciales de un sistema como el clima nunca pueden conocerse con total precisión. Este problema motivó el desarrollo de la predicción por conjuntos , en la que se realizan una serie de predicciones a partir de condiciones iniciales perturbadas. ^[15]

Desde entonces, algunos científicos han argumentado que el sistema meteorológico no es tan sensible a las condiciones iniciales como se creía anteriormente. ^[16] David Orrell sostiene que el principal factor que contribuye al error de previsión meteorológica es el error del modelo, y que la sensibilidad a las condiciones iniciales desempeña un papel relativamente pequeño. ^{[17] [18]} Stephen Wolfram también señala que las ecuaciones de Lorenz están muy simplificadas y no contienen términos que representen efectos viscosos; cree que estos términos tenderían a amortiguar pequeñas perturbaciones. ^[19] Estudios recientes que utilizaron modelos de Lorenz generalizados que incluían términos disipativos adicionales y no linealidad sugirieron que se requiere un parámetro de calentamiento mayor para el inicio del caos. ^[20]

Si bien el "efecto mariposa" a menudo se explica como sinónimo de dependencia sensible de las condiciones iniciales del tipo descrito por Lorenz en su artículo de 1963 (y observado previamente por Poincaré), la metáfora de la mariposa se aplicó originalmente ^[1] al trabajo que publicó en 1969 ^[21] que llevó la idea un paso más allá. Lorenz propuso un modelo matemático de cómo los pequeños movimientos en la atmósfera aumentan de escala para afectar a sistemas más grandes. Encontró que los sistemas en ese modelo sólo podían predecirse hasta un punto específico en el futuro, y más allá de eso, reducir el error en las condiciones iniciales no aumentaría la previsibilidad (siempre que el error no sea cero). Esto demostró que un sistema determinista podría ser "observativamente indistinguible" de uno no determinista en términos de previsibilidad. Reexámenes recientes de este artículo sugieren que ofrece un desafío importante a la idea de que nuestro universo es determinista, comparable a los desafíos que ofrece la física cuántica. ^{[22] [23]}

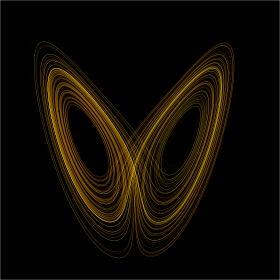
En el libro titulado La Esencia del Caos publicado en 1993, ^[24] Lorenz definió el efecto mariposa como: "El fenómeno de que una pequeña alteración en el estado de un sistema dinámico hará que los estados posteriores difieran mucho de los estados que habrían seguido sin él". la alteración." Esta característica es la misma que la dependencia sensible de las soluciones en las condiciones iniciales (SDIC) en . ^[3] En el mismo libro, Lorenz aplicó la actividad del esquí y desarrolló un modelo de esquí idealizado para revelar la sensibilidad de los caminos que varían en el tiempo a las posiciones iniciales. Se determina un horizonte de previsibilidad antes del inicio de la SDIC. ^[25]

Ilustraciones

Teoría y definición matemática.

La recurrencia , el retorno aproximado de un sistema a sus condiciones iniciales, junto con la dependencia sensible de las condiciones iniciales, son los dos ingredientes principales del movimiento caótico. Tienen la consecuencia práctica de hacer que sistemas complejos , como el tiempo , sean difíciles de predecir más allá de un cierto rango de tiempo (aproximadamente una semana en el caso del tiempo), ya que es imposible medir las condiciones atmosféricas iniciales con total precisión.

Un sistema dinámico muestra una dependencia sensible de las condiciones iniciales si los puntos arbitrariamente juntos se separan con el tiempo a una velocidad exponencial. La definición no es topológica, sino esencialmente métrica. Lorenz ^[24] definió la dependencia sensible de la siguiente manera:

Propiedad que caracteriza a una órbita (es decir, una solución) si la mayoría de las demás órbitas que pasan cerca de ella en algún momento no permanecen cerca de ella a medida que avanza el tiempo.

Si M es el espacio de estados para el mapa , entonces muestra una dependencia sensible a las condiciones iniciales si para cualquier x en M y cualquier δ > 0, hay y en M , con una distancia d (. , .) tal que y tal que ${\displaystyle f^{t}}$ ${\displaystyle f^{t}}$ ${\displaystyle 0<d(x,y)<\delta }$

${\displaystyle d(f^{\tau }(x),f^{\tau }(y))>\mathrm {e} ^{a\tau }\,d(x,y)}$

para algún parámetro positivo a . La definición no requiere que todos los puntos de una vecindad se separen del punto base x , pero requiere un exponente de Lyapunov positivo . Además de un exponente de Lyapunov positivo, la limitación es otra característica importante dentro de los sistemas caóticos. ^[26]

El marco matemático más simple que muestra una dependencia sensible de las condiciones iniciales lo proporciona una parametrización particular del mapa logístico :

${\displaystyle x_{n+1}=4x_{n}(1-x_{n}),\quad 0\leq x_{0}\leq 1,}$

que, a diferencia de la mayoría de los mapas caóticos, tiene una solución de forma cerrada :

${\displaystyle x_{n}=\sin ^{2}(2^{n}\theta \pi )}$

donde el parámetro de condición inicial está dado por . Para racional , después de un número finito de iteraciones , se asigna a una secuencia periódica . Pero casi todos son irracionales y, en el caso de lo irracional , nunca se repite: no es periódico. Esta ecuación de solución demuestra claramente las dos características clave del caos: estiramiento y plegado: el factor 2 ⁿ muestra el crecimiento exponencial del estiramiento, lo que resulta en una dependencia sensible de las condiciones iniciales (el efecto mariposa), mientras que la función seno al cuadrado se mantiene plegada dentro del rango [0, 1]. ${\displaystyle \theta }$ ${\displaystyle \theta ={\tfrac {1}{\pi }}\sin ^{-1}(x_{0}^{1/2})}$ ${\displaystyle \theta }$ ${\displaystyle x_{n}}$ ${\displaystyle \theta }$ ${\displaystyle \theta }$ ${\displaystyle x_{n}}$ ${\displaystyle x_{n}}$

En sistemas físicos

en el clima

El efecto mariposa es más familiar en términos de clima; se puede demostrar fácilmente en modelos estándar de predicción del tiempo, por ejemplo. Los científicos del clima James Annan y William Connolley explican que el caos es importante en el desarrollo de métodos de predicción del tiempo; Los modelos son sensibles a las condiciones iniciales. Añaden la advertencia: "Por supuesto, la existencia de una mariposa desconocida batiendo sus alas no tiene relación directa con los pronósticos meteorológicos, ya que una perturbación tan pequeña tardará demasiado en crecer hasta alcanzar un tamaño significativo, y tenemos muchas más noticias inmediatas". incertidumbres de las que preocuparse. Por lo tanto, el impacto directo de este fenómeno en la predicción del tiempo es a menudo algo erróneo." ^[27] Los dos tipos de efectos mariposa, incluida la dependencia sensible de las condiciones iniciales, ^[3] y la capacidad de una pequeña perturbación para crear una circulación organizada a grandes distancias, ^[1] no son exactamente iguales. ^[28] Se ha documentado una comparación de los dos tipos de efectos mariposa ^{[1] [3]} y el tercer tipo de efecto mariposa ^{[21] [22] [23] . [29]} En estudios recientes, ^{[25] [30]} se informó que tanto los modelos lineales meteorológicos como los no meteorológicos han demostrado que la inestabilidad juega un papel en la producción de un efecto mariposa, que se caracteriza por un crecimiento exponencial breve pero significativo resultante de una pequeña perturbación.

Según Lighthill (1986), ^[31] la presencia de SDIC (comúnmente conocido como efecto mariposa) implica que los sistemas caóticos tienen un límite de previsibilidad finito. En una revisión de la literatura, ^[32] se encontró que la perspectiva de Lorenz sobre el límite de previsibilidad se puede condensar en la siguiente afirmación:

• (A). El modelo de Lorenz 1963 reveló cualitativamente la esencia de una previsibilidad finita dentro de un sistema caótico como la atmósfera. Sin embargo, no determinó un límite preciso para la previsibilidad de la atmósfera.
• (B). En la década de 1960, el límite de previsibilidad de dos semanas se estimó originalmente basándose en un tiempo de duplicación de cinco días en modelos del mundo real. Desde entonces, este hallazgo ha sido documentado en Charney et al. (1966) ^{[33] [34]} y se ha convertido en un consenso.

Recientemente, se creó un breve vídeo para presentar la perspectiva de Lorenz sobre el límite de previsibilidad. ^[35]

Al revelar la coexistencia de atractores caóticos y no caóticos dentro de los modelos de Lorenz, Shen y sus colegas propusieron una visión revisada de que "el clima posee caos y orden", en contraste con la visión convencional de que "el clima es caótico". ^{[36] [37] [38]} Como resultado, no siempre aparece una dependencia sensible de las condiciones iniciales (SDIC). Es decir, SDIC aparece cuando dos órbitas (es decir, soluciones) se convierten en el atractor caótico; no aparece cuando dos órbitas se mueven hacia el mismo punto atractor. La animación anterior para el movimiento de doble péndulo proporciona una analogía. Para ángulos de oscilación grandes, el movimiento del péndulo suele ser caótico. ^{[39] [40]} En comparación, para ángulos de oscilación pequeños, los movimientos no son caóticos. La multiestabilidad se define cuando un sistema (por ejemplo, el sistema de doble péndulo ) contiene más de un atractor acotado que depende sólo de las condiciones iniciales. La multiestabilidad se ilustró usando kayak en la Figura del lado derecho (es decir, Figura 1 de ^[41] ), donde la aparición de fuertes corrientes y un área estancada sugiere inestabilidad y estabilidad local, respectivamente. Como resultado, cuando dos kayaks se mueven a lo largo de fuertes corrientes, sus trayectorias muestran SDIC. Por otro lado, cuando dos kayaks se mueven hacia un área estancada, quedan atrapados y no muestran un SDIC típico (aunque puede ocurrir un transitorio caótico). Tales características de SDIC o de ninguna SDIC sugieren dos tipos de soluciones e ilustran la naturaleza de la multiestabilidad.

Al tomar en consideración la multiestabilidad variable en el tiempo que está asociada con la modulación de procesos a gran escala (por ejemplo, forzamiento estacional) y la retroalimentación agregada de procesos a pequeña escala (por ejemplo, convección), la visión revisada anterior se refina de la siguiente manera:

"La atmósfera posee caos y orden; incluye, como ejemplos, sistemas organizados emergentes (como los tornados) y fuerzas que varían en el tiempo a partir de estaciones recurrentes". ^{[41] [42]}

En mecánica cuántica

El potencial de dependencia sensible de las condiciones iniciales (el efecto mariposa) se ha estudiado en varios casos en física semiclásica y cuántica, incluidos átomos en campos fuertes y el problema anisotrópico de Kepler . ^{[43] [44]} Algunos autores han argumentado que no se espera una dependencia extrema (exponencial) de las condiciones iniciales en tratamientos cuánticos puros; ^{[45] [46]} sin embargo, la dependencia sensible de las condiciones iniciales demostrada en el movimiento clásico está incluida en los tratamientos semiclásicos desarrollados por Martin Gutzwiller ^[47] y John B. Delos y colaboradores. ^[48] ​​La teoría de matrices aleatorias y las simulaciones con ordenadores cuánticos demuestran que algunas versiones del efecto mariposa en la mecánica cuántica no existen. ^[49]

Otros autores sugieren que el efecto mariposa se puede observar en sistemas cuánticos. Zbyszek P. Karkuszewski et al. Considere la evolución temporal de los sistemas cuánticos que tienen hamiltonianos ligeramente diferentes . Investigan el nivel de sensibilidad de los sistemas cuánticos a pequeños cambios en sus hamiltonianos determinados. ^[50] David Poulin y otros. presentó un algoritmo cuántico para medir la caída de la fidelidad, que "mide la velocidad a la que estados iniciales idénticos divergen cuando se someten a dinámicas ligeramente diferentes". Consideran que la decadencia de la fidelidad es "el análogo cuántico más cercano al efecto mariposa (puramente clásico)". ^[51] Mientras que el efecto mariposa clásico considera el efecto de un pequeño cambio en la posición y/o velocidad de un objeto en un sistema hamiltoniano dado , el efecto mariposa cuántico considera el efecto de un pequeño cambio en el sistema hamiltoniano con un valor inicial dado. posición y velocidad. ^{[52] [53]} Este efecto mariposa cuántico se ha demostrado experimentalmente. ^[54] Los tratamientos cuánticos y semiclásicos de la sensibilidad del sistema a las condiciones iniciales se conocen como caos cuántico . ^{[45] [52]}

En la cultura popular

Ver también

• efecto avalancha
• Cúspide conductual
• Fallo en cascada
• Teoría de la catástrofe
• Causalidad
• Reacción en cadena
• clapotis
• Determinismo
• efecto dominó
• sistema dinámico
• fractales
• Gran controversia sobre los estribo
• Mariposa de innovación
• síndrome de kessler
• La cúpula de Norton.
• Análisis numérico
• Punto de divergencia
• Retroalimentación positiva
• Potencialidad y actualidad
• Heurística de representatividad
• Efecto dominó
• Efecto bola de nieve
• La congestión del tráfico
• ciclogénesis tropical
• Consecuencias no deseadas

Referencias

1. "Previsibilidad: ¿El aleteo de una mariposa en Brasil provoca un tornado en Texas?" (PDF) . Archivado (PDF) desde el original el 9 de octubre de 2022 . Consultado el 23 de diciembre de 2021 .
2. "Cuando Lorenz descubrió el efecto mariposa". 22 de mayo de 2015 . Consultado el 23 de diciembre de 2021 .
3. Lorenz, Edward N. (marzo de 1963). "Flujo no periódico determinista". Revista de Ciencias Atmosféricas . 20 (2): 130-141. Código Bib : 1963JAtS...20..130L. doi : 10.1175/1520-0469(1963)020<0130:dnf>2.0.co;2 .
4. Rouvas-Nicolis, Catherine; Nicolis, Gregoire (4 de mayo de 2009). "Efecto mariposa". Scholarpedia . vol. 4. pág. 1720. Código bibliográfico : 2009SchpJ...4.1720R. doi : 10.4249/scholarpedia.1720 . Archivado desde el original el 2 de enero de 2016 . Consultado el 2 de enero de 2016 .
5. Algunas notas históricas: Historia de la teoría del caos Archivado el 19 de julio de 2006 en la Wayback Machine.
6. Steves, Bonnie; Maciejewski, AJ (septiembre de 2001). Las aplicaciones del universo inquieto de la dinámica gravitacional de N-cuerpos a los sistemas planetarios estelares y galácticos. Estados Unidos: Prensa CRC. ISBN 0750308222. Consultado el 6 de enero de 2014 .
7. Maquinaria informática e inteligencia
8. Flam, Faye (15 de junio de 2012). "La física de" A Sound of Thunder "de Ray Bradbury"". El Philadelphia Inquirer . Archivado desde el original el 24 de septiembre de 2015 . Consultado el 2 de septiembre de 2015 .
9. Gleick, James (1987). Caos: haciendo una nueva ciencia . Vikingo. pag. 16.ISBN _ 0-8133-4085-3.
10. Motter, Adilson E.; Campbell, David K. (2013). "Caos a los cincuenta". Física hoy . 66 (5): 27–33. arXiv : 1306.5777 . Código bibliográfico : 2013PhT....66e..27M. doi :10.1063/PT.3.1977. S2CID  54005470.
11. Registro de citas de Google Scholar
12. "Parte 19". Cs.ualberta.ca. 1960-11-22. Archivado desde el original el 17 de julio de 2009 . Consultado el 8 de junio de 2014 .
13. Lorenz, Edward N. (1963). "La previsibilidad del flujo hidrodinámico" (PDF) . Transacciones de la Academia de Ciencias de Nueva York . 25 (4): 409–432. doi :10.1111/j.2164-0947.1963.tb01464.x. Archivado (PDF) desde el original el 10 de octubre de 2014 . Consultado el 1 de septiembre de 2014 .
14. "Los efectos mariposa: variaciones de un meme". AP42 ...y todo . Archivado desde el original el 11 de noviembre de 2011 . Consultado el 3 de agosto de 2011 .
15. Bosques, Austin (2005). Predicción meteorológica a medio plazo: el enfoque europeo; La historia del Centro Europeo de Previsiones Meteorológicas a Plazo Medio . Nueva York: Springer. pag. 118.ISBN _ 978-0387269283.
16. Orrell, David; Smith, Leonardo; Barkmeijer, enero; Palmer, Tim (2001). "Error de modelo en la previsión meteorológica". Procesos no lineales en geofísica . 9 (6): 357–371. Código Bib : 2001NPGeo...8..357O. doi : 10.5194/npg-8-357-2001 .
17. Orrell, David (2002). "Papel de la métrica en el crecimiento del error de pronóstico: ¿Qué tan caótico es el clima?". Dinos . 54A (4): 350–362. Código Bib : 2002 TellA..54..350O. doi : 10.3402/tellusa.v54i4.12159 .
18. Orrell, David (2012). Verdad o belleza: la ciencia y la búsqueda del orden . New Haven: Prensa de la Universidad de Yale. pag. 208.ISBN _ 978-0300186611.
19. Wolfram, Stephen (2002). Un nuevo tipo de ciencia . Medios Wolfram. pag. 998.ISBN _ 978-1579550080.
20. Shen, Bo-Wen (2019). "Retroalimentación negativa agregada en un modelo de Lorenz generalizado". Revista Internacional de Bifurcación y Caos . 29 (3): 1950037–1950091. Código Bib : 2019IJBC...2950037S. doi : 10.1142/S0218127419500378 . S2CID  132494234.
21. Lorenz, Edward N. (junio de 1969). "La previsibilidad de un flujo que posee muchas escalas de movimiento". Dinos . XXI (3): 289–297. Bibcode : 1969 Dile...21..289L. doi :10.1111/j.2153-3490.1969.tb00444.x.
22. Tim, Palmer (19 de mayo de 2017). "El efecto mariposa: ¿qué significa realmente?". Canal de Youtube del Departamento de Matemáticas de la Universidad de Oxford . Archivado desde el original el 31 de octubre de 2021 . Consultado el 13 de febrero de 2019 .
23. Emanuel, Kerry (26 de marzo de 2018). "Edward N. Lorenz y el fin del universo cartesiano". Canal de Youtube del Departamento de Ciencias de la Tierra, Atmosféricas y Planetarias del MIT . Archivado desde el original el 31 de octubre de 2021 . Consultado el 13 de febrero de 2019 .
24. Lorenz, Edward N. (1993). La esencia del caos. Londres: UCL Press. ISBN 0-203-21458-7. OCLC  56620850.
25. Shen, Bo-Wen; Pielke, Roger A.; Zeng, Xubin (7 de mayo de 2022). "Un punto de silla y dos tipos de sensibilidades dentro de los modelos Lorenz 1963 y 1969". Atmósfera . 13 (5): 753. Bibcode : 2022Atmos..13..753S. doi : 10.3390/atmos13050753 . ISSN  2073-4433.
26. W., Jordania, Dominic (2011). Ecuaciones diferenciales ordinarias no lineales: una introducción para científicos e ingenieros. Universidad de Oxford. Prensa. ISBN 978-0-19-920825-8. OCLC  772641393.{{cite book}}: CS1 maint: multiple names: authors list (link)
27. "Caos y clima". Clima real. 4 de noviembre de 2005. Archivado desde el original el 2 de julio de 2014 . Consultado el 8 de junio de 2014 .
28. Shen, Bo-Wen (1 de mayo de 2014). "Retroalimentación no lineal en un modelo de Lorenz de cinco dimensiones". Revista de Ciencias Atmosféricas . 71 (5): 1701-1723. Código Bib : 2014JAtS...71.1701S. doi :10.1175/JAS-D-13-0223.1. ISSN  0022-4928. S2CID  123683839.
29. Shen, Bo-Wen; Pielke, Roger A.; Zeng, Xubin; Cui, Jialin; Faghih-Naini, Sara; Paxson, Wei; Atlas, Robert (4 de julio de 2022). "Tres tipos de efectos mariposa dentro de los modelos de Lorenz". Enciclopedia . 2 (3): 1250-1259. doi : 10.3390/enciclopedia2030084 . ISSN  2673-8392.
30. Saiki, Yoshitaka; Yorke, James A. (2 de mayo de 2023). "¿Puede el aleteo de las alas de una mariposa trasladar un tornado a Texas, sin caos?". Atmósfera . 14 (5): 821. Bibcode : 2023Atmos..14..821S. doi : 10.3390/atmos14050821 . ISSN  2073-4433.
31. Lighthill, James (8 de septiembre de 1986). "El fracaso de la previsibilidad recientemente reconocido en la dinámica newtoniana". Actas de la Royal Society de Londres. A. Ciencias Matemáticas y Físicas . 407 (1832): 35–50. Código Bib : 1986RSPSA.407...35L. doi :10.1098/rspa.1986.0082. ISSN  0080-4630. S2CID  86552243.
32. Shen, Bo-Wen; Pielke, Roger A.; Zeng, Xubin; Zeng, Xiping (22 de julio de 2023). "La visión de Lorenz sobre el límite de previsibilidad de la atmósfera". Enciclopedia . 3 (3): 887–899. doi : 10.3390/enciclopedia3030063 . ISSN  2673-8392. Este artículo incorpora texto de esta fuente, que está disponible bajo la licencia CC BY 4.0.
33. La viabilidad de un experimento de análisis y observación global. 1966-01-01. doi :10.17226/21272. ISBN 978-0-309-35922-1.
34. GARP (1 de marzo de 1969). "Una guía para GARP". Toro. América. Meteorito. Soc . 50 (3): 136-141. Código bibliográfico : 1969BAMS...50..136.. doi : 10.1175/1520-0477-50.3.136 .
35. Shen, Bo-Wen; Pielke, Sr., Roger; Zeng, Xubin; Zeng, Xiping (13 de septiembre de 2023). "La opinión de Lorenz sobre el límite de previsibilidad". Pub de enciclopedia . Consultado el 13 de septiembre de 2023 .
36. Shen, Bo-Wen; Pielke, Roger A.; Zeng, Xubin; Baik, Jong-Jin; Faghih-Naini, Sara; Cui, Jialin; Atlas, Robert (1 de enero de 2021). "¿Es el clima caótico?: Coexistencia de caos y orden dentro de un modelo de Lorenz generalizado". Boletín de la Sociedad Meteorológica Estadounidense . 102 (1): E148-E158. Código Bib : 2021BAMS..102E.148S. doi : 10.1175/BAMS-D-19-0165.1 . ISSN  0003-0007. S2CID  208369617.
37. Shen, Bo-Wen; Pielke, RA Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R.; Reyes, TAL (2021). "¿Es el clima caótico? Atractores caóticos y no caóticos coexistentes dentro de los modelos de Lorenz". En Skiadas, Christos H.; Dimotikalis, Yiannis (eds.). 13º Congreso Internacional de Simulación y Modelado Caótico . Procedimientos Springer en complejidad. Cham: Editorial Internacional Springer. págs. 805–825. doi :10.1007/978-3-030-70795-8_57. ISBN 978-3-030-70795-8. S2CID  245197840.
38. Anthes, Richard A. (14 de agosto de 2022). "Previsibilidad y predicciones". Atmósfera . 13 (8): 1292. Bibcode : 2022Atmos..13.1292A. doi : 10.3390/atmos13081292 . ISSN  2073-4433.
39. Richter, PH; Scholz, H.-J. (1984), "Caos en la mecánica clásica: el doble péndulo", Fenómenos estocásticos y comportamiento caótico en sistemas complejos , Springer Series in Synergetics, Berlín, Heidelberg: Springer Berlin Heidelberg, vol. 21, págs. 86–97, doi :10.1007/978-3-642-69591-9_9, ISBN 978-3-642-69593-3, recuperado el 11 de julio de 2022
40. Shinbrot, Troy, Celso A Grebogi, Jack Wisdom, James A Yorke (1992). "Caos en un doble péndulo". Revista Estadounidense de Física . 60 (6): 491–499. Código bibliográfico : 1992AmJPh..60..491S. doi :10.1119/1.16860.{{cite journal}}: CS1 maint: multiple names: authors list (link)
41. Shen, Bo-Wen; Pielke Sr., Roger Pielke; Zeng, Xubin; Cui, Jialin; Faghih-Naini, Sara; Paxson, Wei; Kesarkar, Amit; Zeng, Xiping; Atlas, Robert (12 de noviembre de 2022). "La doble naturaleza del caos y el orden en la atmósfera". Atmósfera . 13 (11): 1892. Bibcode : 2022Atmos..13.1892S. doi : 10.3390/atmos13111892 . ISSN  2073-4433. El texto se copió de esta fuente, que está disponible bajo una licencia internacional Creative Commons Attribution 4.0.
42. Shen, Bo-Wen (21 de febrero de 2023). "Explorando la teoría del caos para la inestabilidad y la multiestabilidad". YouTube .
43. Heller, EJ; Tomsovic, S. (julio de 1993). "Mecánica cuántica posmoderna". Física hoy . 46 (7): 38–46. Código Bib : 1993PhT....46g..38H. doi : 10.1063/1.881358.
44. Gutzwiller, Martín C. (1990). Caos en la mecánica clásica y cuántica . Nueva York: Springer-Verlag. ISBN 0-387-97173-4.
45. Rudnick, Ze'ev (enero de 2008). "¿Qué es... el Caos Cuántico?" (PDF) . Avisos de la Sociedad Matemática Estadounidense . Archivado (PDF) desde el original el 2 de octubre de 2009.
46. Baya, Michael (1989). "Caología cuántica, no caos cuántico". Escritura física . 40 (3): 335–336. Código bibliográfico : 1989PhyS...40..335B. doi :10.1088/0031-8949/40/3/013. S2CID  250776260.
47. Gutzwiller, Martín C. (1971). "Órbitas periódicas y condiciones de cuantificación clásicas". Revista de Física Matemática . 12 (3): 343. Código bibliográfico : 1971JMP....12..343G. doi : 10.1063/1.1665596.
48. Gao, J. y Delos, JB (1992). "Teoría de órbita cerrada de oscilaciones en secciones transversales de fotoabsorción atómica en un campo eléctrico fuerte. II. Derivación de fórmulas". Revisión física A. 46 (3): 1455-1467. Código bibliográfico : 1992PhRvA..46.1455G. doi :10.1103/PhysRevA.46.1455. PMID  9908268. S2CID  7877923.
49. Yan, contenedor; Sinitsyn, Nikolai A. (2020). "Recuperación de información dañada y correlacionadores ordenados fuera de tiempo". Cartas de revisión física . 125 (4): 040605. arXiv : 2003.07267 . Código Bib : 2020PhRvL.125d0605Y. doi : 10.1103/PhysRevLett.125.040605. PMID  32794812. S2CID  212725801.
50. Karkuszewski, Zbyszek P.; Jarzynski, Christopher; Zurek, Wojciech H. (2002). "Ambientes caóticos cuánticos, efecto mariposa y decoherencia". Cartas de revisión física . 89 (17): 170405. arXiv : quant-ph/0111002 . Código Bib : 2002PhRvL..89q0405K. doi : 10.1103/PhysRevLett.89.170405. PMID  12398653. S2CID  33363344.
51. Poulin, David; Blume-Kohout, Robin; Laflamme, Raymond y Ollivier, Harold (2004). "Aceleración exponencial con un solo bit de información cuántica: medición de la caída de fidelidad promedio". Cartas de revisión física . 92 (17): 177906. arXiv : quant-ph/0310038 . Código bibliográfico : 2004PhRvL..92q7906P. doi : 10.1103/PhysRevLett.92.177906. PMID  15169196. S2CID  6218604.
52. Poulin, David. "Una guía aproximada del caos cuántico" (PDF) . Archivado desde el original (PDF) el 4 de noviembre de 2010.
53. Peres, A. (1995). Teoría cuántica: conceptos y métodos . Dordrecht: Académico Kluwer.
54. Lee, Jae-Seung y Khitrin, AK (2004). "Amplificador cuántico: medición con espines entrelazados". Revista de Física Química . 121 (9): 3949–51. Código Bib : 2004JChPh.121.3949L. doi : 10.1063/1.1788661 . PMID  15332940.

Otras lecturas

• James Gleick , Caos: Haciendo una nueva ciencia , Nueva York: Viking, 1987. 368 págs.
• Devaney, Robert L. (2003). Introducción a los sistemas dinámicos caóticos . Prensa de Westview. ISBN 0670811785.
• Hilborn, Robert C. (2004). "Gaviotas, mariposas y saltamontes: una breve historia del efecto mariposa en dinámica no lineal". Revista Estadounidense de Física . 72 (4): 425–427. Código Bib : 2004AmJPh..72..425H. doi :10.1119/1.1636492.
• Bradbury, Ray. "Un sonido de trueno". Collier's. 28 de junio de 1952

enlaces externos

• Clima y caos: la obra de Edward N. Lorenz. Un breve documental que explica el "efecto mariposa" en el contexto de la obra de Lorenz.
• El hiperlibro del caos. Una introducción al caos y los fractales.
• Dizikes, Peter (8 de junio de 2008). "El significado de la mariposa. Por qué a la cultura pop le encanta el 'efecto mariposa' y se equivoca totalmente". El Boston Globe . Boston, Massachusetts . Consultado el 19 de junio de 2022 .
• Instituto de Sistemas Complejos de Nueva Inglaterra - Conceptos: Efecto Mariposa
• CaosBook.org. Libro de texto de posgrado avanzado sobre caos (sin fractales)
• Weisstein, Eric W. "Efecto mariposa". MundoMatemático .