Período orbital

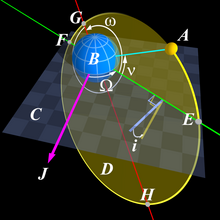
El período orbital es el tiempo que le toma a un astro recorrer su órbita.Cuando se trata de objetos que orbitan alrededor del sol existen dos tipos: El período sideral y el sinódico difieren, ya que la Tierra, a su vez, da vueltas alrededor del Sol.Este es el período orbital en un marco de referencia inercial (no giratorio).El período draconiano o período dracónico es el tiempo que transcurre entre dos pasajes del objeto a través de su nodo ascendente, el punto de su órbita donde cruza la eclíptica desde el hemisferio sur hasta el hemisferio norte.Aunque el plano de la eclíptica a menudo se mantiene fijo en la posición que ocupaba en una época específica, el plano orbital del objeto todavía precesa, haciendo que el período draconítico difiera del período sideral.donde: Obsérvese que este periodo es válido para todas las órbitas cerradas, es decir, circulares y elípticas, sin importar su excentricidad.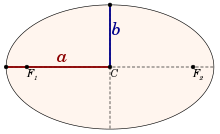Inversamente podemos calcular el semi-eje mayor de una órbita dado su periodo orbital con la siguiente expresión:Podríamos por ejemplo calcular un caso curioso aunque poco viable en la práctica.En la mecánica celeste, cuando hay que tener en cuenta las masas de ambos cuerpos orbitales, el período orbital T puede calcularse de la siguiente manera:[1]​ donde: Tenga en cuenta que el período orbital es independiente del tamaño: para un modelo a escala sería el mismo, cuando las densidades son las mismas (véase también Orbit § Scaling in gravity).El signo de ±360° es una suma si el astro da una vuelta a su órbita en menor tiempo que la Tierra —sea un planeta interior (diferente a Marte o la propia Tierra) o la Luna—, es una resta si el astro da una vuelta a su órbita en mayor tiempo que la Tierra —sea Marte, un planeta exterior o un planeta enano—.Si estamos en la Tierra y observamos la luna a través de los días veremos que tarda aproximadamente 29 d 12 h 44 min en su periodo sinódico (aparente desde la Tierra con respecto al sol) o bien 29.530556 días, lo cual es el valor de S. Sabemos que la Tierra tarda aproximadamente 365.256363 días en dar una vuelta al sol,[2]​ lo cual será nuestro valor T. La operación queda así: El signo es positivo dado que da una vuelta a su propia órbita más rápido que la Tierra a la suya.