Muestreo (estadística)
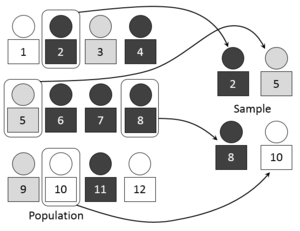
[1] Al elegir una muestra aleatoria se espera conseguir que sus propiedades sean extrapolables a la población.
En las investigaciones llevadas por empresarios y de la medicina se usa muestreo extensivamente en recoger información sobre poblaciones.
La variable que asocia a cada muestra su probabilidad de extracción, sigue la llamada distribución muestral.
El éxito de la práctica estadística se basa en la definición precisa del problema.
En el muestreo, esto incluye definir la "población" de la que se extrae nuestra muestra.
Una población puede definirse como el conjunto de personas o elementos con las características que se desea comprender.
Por ejemplo, un fabricante tiene que decidir si un lote de material de producción tiene la calidad suficiente para entregárselo al cliente o si debe desecharse o reelaborarse debido a su mala calidad.
Consideraciones similares surgen cuando se toman medidas repetidas de alguna característica física, como la conductividad eléctrica del cobre.
En tales casos, la teoría del muestreo puede tratar a la población observada como una muestra de una "superpoblación" mayor.
El tiempo invertido en precisar la población muestreada y la población objeto de estudio suele estar bien empleado, ya que plantea muchas cuestiones, ambigüedades y preguntas que, de otro modo, se habrían pasado por alto en esta fase.
Sin embargo, en el caso más general esto no suele ser posible ni práctico.
Ejemplo: Queremos estimar los ingresos totales de los adultos que viven en una calle determinada.
En la investigación comercial y médica, el muestreo se usa ampliamente para recopilar información sobre una población.
Para determinar en qué fecha se producirá la primera extracción hay que elegir al azar un número entre 1 y K; de ahí en adelante tomar uno de cada K a intervalos regulares.
Para una descripción general del muestreo estratificado y los métodos de inferencia asociados con este procedimiento, suponemos que la población está dividida en h subpoblaciones o estratos de tamaños conocidos N1, N2,..., Nh tal que las unidades en cada estrato sean homogéneas respecto a la característica en cuestión.
Por ejemplo, si es necesario construir una muestra de profesores de primaria en un país determinado, estos pueden subdividirse en unidades primarias representadas por circunscripciones didácticas y unidades secundarias que serían los propios profesores.
Homogéneo significa, en el contexto de la estratificación, que no hay mucha variabilidad.
Por ejemplo, si se estudia la estatura de una población, es bueno distinguir entre los estratos mujeres y hombres porque se espera que, dentro de ellos, haya menos variabilidad, es decir, sean menos heterogéneos.
Dicho de otro modo, no hay tantas diferencias entre unas estaturas y otras dentro del estrato que en la población total.
El espacio muestral es: Conjunto formado por todos los resultados posibles de un experimento aleatorio.
Por tal motivo, se busca seleccionar a individuos que tienen un conocimiento profundo del tema bajo estudio y se considera que la información aportada por esas personas es vital para la toma de decisiones.
Consiste en identificar sujetos que se incluirán en la muestra a partir de los propios entrevistados.