Extensión (óptica)
En términos físicos, la extensión puede considerarse como la variación del volumen abarcado por un haz de luz en el espacio.
El término proviene del francés "étendue géométrique", que significa "extensión geométrica".
Otras denominaciones para esta propiedad son aceptancia, rendimiento, comprensión lumínica, recolección de luz o poder de captación, extensión óptica, extensión geométrica y producto AΩ.
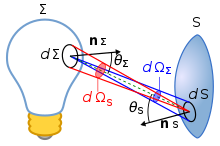
[5] De acuerdo con la definición anterior, la extensión del cruce de luz dΣ hacia dS viene dada por: donde dΩΣ es el ángulo sólido definido por el área dS en el área dΣ.
La extensión de todo el sistema es entonces: Si ambas superficies dΣ y dS están inmersas en el aire (o en el vacío), n = 1, la expresión anterior para la extensión pueden escribirse como donde FdΣ→dS es el factor visual entre las superficies diferenciales dΣ y dS.
Las direcciones de la luz entrante y refractada están contenidas en un plano que forma un ángulo φ con el eje x, que define estas direcciones en coordenadas esféricas.
La radiancia espectral de una superficie está relacionado con la extensión por: donde A medida que la luz viaja a través de un sistema óptico ideal, tanto la extensión como el flujo radiante se conservan.
En sistemas reales, la extensión puede aumentar (por ejemplo, debido a la dispersión) o el flujo radiante puede disminuir (por ejemplo, debido a la absorción) y, por lo tanto, la radiancia básica puede disminuir.
En el contexto de la óptica hamiltoniana, en un punto del espacio, un rayo de luz puede estar completamente definido por un punto r = (x, y, z), un vector unidad v = (cos αX, cos αY, cos αZ) que indica su dirección y el índice de refracción n en el punto r. El momento óptico del rayo en ese punto está definido por donde | | p | | = n. La geometría del vector de momento óptico se ilustra en la figura "momento óptico".
En coordenadas esféricas p puede escribirse como a partir del cual y por lo tanto, para un área infinitesimal dS= dx dy en el plano xy inmerso en un medio de índice de refracción n, la extensión viene dada por que es un volumen infinitesimal en el espacio de fase x, y, p, q.