Cuadrupolo
Un cuadrupolo es una de las distintas configuraciones de múltiples objetos (concretamente cuatro) ligados a fuerzas (como cargas o corrientes eléctricas, o masas gravitatorias), que puede existir en forma ideal, pero que generalmente es solo una parte de un desarrollo multipolar de una estructura más complicada que refleja varios órdenes de complejidad.
, los componentes de Q están definidos por la integral sobre el espacio cartesiano r:[1]
Por ejemplo, un dipolo eléctrico de dos cargas puntuales de signo opuesto y fuerza igual, que no tiene momento monopolar, puede tener un momento cuadrupolar distinto de cero si el origen se aleja del centro de la configuración exactamente entre las dos cargas; o el momento cuadrupolar se puede reducir a cero con el origen en el centro.
Por el contrario, si los momentos monopolares y dipolares desaparecen, pero el momento cuadrupolar no, como por ejemplo con cuatro cargas de la misma fuerza, dispuestas en los vértices de un cuadrado, con signos alternos, entonces el momento cuadrupolar es independiente de las coordenadas.
", como el campo eléctrico o el campo gravitatorio, la contribución al potencial del campo debido a un momento cuadrupolar es: donde R es un vector con origen en el sistema de cargas y n es el vector unitario en la dirección de R. Aquí,
El ejemplo más simple de un cuadrupolo eléctrico consiste en alternar cargas positivas y negativas, dispuestas en las esquinas de un cuadrado.
El momento monopolar (solo la carga total) de esta disposición es cero.
De manera similar, el momento dipolar químico es cero, independientemente del origen de coordenadas que se haya elegido.
Multipolos aún más altos, por ejemplo, de orden 2l, se obtendrían mediante distribuciones dipolares (cuadrupolar, octopolar, ...) de dipolos puntuales (cuadrupolos, octopolos, ...), no monopolos puntuales, de orden inferior, por ejemplo 2l-1.
Todas las fuentes magnéticas conocidas dan campos dipolares.
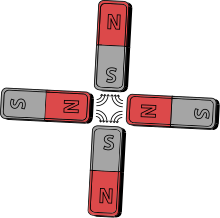
Sin embargo, para componer un cuadrupolo magnético es posible colocar cuatro imanes de barra idénticos perpendiculares entre sí, de manera que el polo norte de uno esté al lado del sur del otro.
Dicha configuración cancela el momento dipolar y da un momento cuadrupolar, y su campo disminuirá a grandes distancias más rápido que el de un dipolo.
Un ejemplo de un cuadrupolo magnético, que involucra imanes permanentes, se representa a la derecha.
Hay cuatro puntas de acero, dos polos norte magnéticos opuestos y dos polos sur magnéticos opuestos.
El acero está magnetizado por una gran corriente eléctrica que fluye en las bobinas de los tubos envueltos alrededor de los polos.
Además, la interacción cuadrupolo-dipolo se puede hallar multiplicando el espín del nucleón no apareado por su átomo principal.
Un momento cuadrupolar magnético cambiante produce radiación electromagnética.
El cuadrupolo de masa es análogo al cuadrupolo de carga eléctrica, donde la densidad de carga simplemente se reemplaza por la densidad de masa y se agrega un signo negativo porque las masas son siempre positivas y la fuerza es atractiva.
El potencial gravitatorio se expresa entonces como: Por ejemplo, debido a que la Tierra está girando, está achatada (aplanada en los polos).
Esto le da un momento cuadrupolar distinto de cero.
Si bien la contribución al campo gravitatorio de la Tierra desde este cuadrupolo es extremadamente importante para los satélites artificiales cercanos a la Tierra, es menos importante para la Luna, porque el término
El momento cuadrupolar de la masa también es importante en la relatividad general porque, si cambia en el tiempo, puede producir ondas gravitatorias, similares a la radiación electromagnética producida por los dipolos oscilantes eléctricos o magnéticos y multipolos superiores.
Sin embargo, solo el cuadrupolo y los momentos superiores pueden irradiar gravitacionalmente.
El monopolo de masa representa la masa-energía total en un sistema que se conserva, por lo que no emite radiación.
[3] El ejemplo más simple y más importante de un sistema radiante es un par de puntos materiales con masas iguales que orbitan entre sí en una órbita circular, una aproximación a, por ejemplo, el caso especial de agujeros negros binarios.
Dado que el momento dipolar es constante, se puede ubicar, por conveniencia, el origen de coordenadas justo entre los dos puntos.
Entonces, el momento dipolar será cero, y si también se escalan las coordenadas de modo que los puntos se encuentren a una unidad de distancia del centro, en dirección opuesta, el momento cuadripolar del sistema simplemente será donde M es la masa de cada punto, y
A medida que orbitan, este vector x girará, lo que significa que primero tendrá un valor distinto de cero y también la segunda derivada temporal (esto es cierto, independientemente de la elección del sistema de coordenadas).
Al igual que la carga eléctrica y los multipolos de corriente contribuyen al campo electromagnético, los multipoles de masa y de corriente de masa contribuyen al campo gravitacional en la relatividad general, causando los llamados efectos gravitomagnéticos.
Sin embargo, las contribuciones de los multipolos actuales serán típicamente mucho más pequeñas que las del cuadrupolo de masas.