Coordenadas toroidales
Las coordenadas toroidales[1] son un sistema de coordenadas tridimensionales ortogonales que resulta de girar la un sistema de coordenadas bipolares bidimensional alrededor del eje que separa sus dos focos.
en coordenadas bipolares se convierten en un anillo de radio
del sistema de coordenadas toroidales; siendo el eje
El anillo focal también se conoce como círculo de referencia.
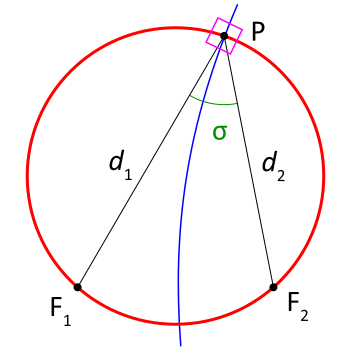
La definición más común de las coordenadas toroidales
a lados opuestos del anillo focal.
Los rangos de coordenadas son
constante corresponden a esferas de diferentes radios de manera que todas pasan a través del anillo focal, pero no son concéntricas.
constante son toros que no se cruzan y de diferentes radios de manera que rodean el anillo focal.
se pueden calcular a partir de las coordenadas cartesianas (x, y, z) de la siguiente manera.
viene dado por la fórmula El radio cilíndrico
del punto P viene dado por y sus distancias a los focos en el plano definido por
es igual al logaritmo del cociente de las distancias focales mientras que
es igual al ángulo entre los rayos y los focos, que puede determinarse a partir del teorema del coseno O explícitamente, incluido el signo, donde
Las transformaciones entre coordenadas cilíndricas y toroidales se pueden expresar en notación compleja como Los factores de escala para las coordenadas toroidales
son iguales entre sí mientras que el factor de escala azimutal es igual a Por lo tanto, el elemento de volumen infinitesimal es igual a El laplaciano viene dado por Para un campo vectorial el vector laplaciano viene dado por Otros operadores diferenciales como
sustituyendo los factores de escala en las fórmulas generales para las coordenadas ortogonales.
Haciendo la sustitución se obtiene una ecuación separable.
Una solución particular obtenida por el método de separación de variables es: donde cada función es una combinación lineal de: donde P y Q son las funciones de Legendre asociadas del primer y segundo tipo.
Estas funciones de Legendre a menudo se denominan armónicos toroidales.
Los armónicos toroidales tienen muchas propiedades interesantes.
Si se realiza una sustitución de variable
(la convención es no escribir el orden cuando desaparece) y
son las integrales elípticas completas de primer tipo y de segundo tipo respectivamente.
Ejemplos típicos serían el potencial eléctrico y el campo eléctrico de un toro conductor o, en el caso degenerado, un anillo de corriente eléctrica (Hulme 1982).
Alternativamente, se puede hacer una sustitución diferente (Andrews 2006) donde Nuevamente se obtiene una ecuación separable.
Una solución particular obtenida por el método de separación de variables es entonces donde cada función es una combinación lineal de Téngase en cuenta que aunque los armónicos toroidales se utilizan nuevamente para la función T , el argumento es
Este método es útil para situaciones en las que las condiciones de contorno son independientes del ángulo esférico
, como el anillo cargado, un semiplano infinito o dos planos paralelos.
Para identidades que relacionan los armónicos toroidales con el argumento del coseno hiperbólico con los del argumento de la cotangente hiperbólica, véanse las fórmulas de Whipple.