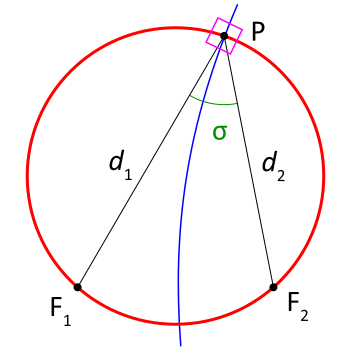
Coordenadas bipolares
Además, existe un tercer sistema también basado en dos polos (las coordenadas biangulares).
El término bipolar se usa además en ocasiones para describir otras curvas que tienen dos puntos singulares (focos), como elipses, hipérbolas y óvalos de Cassini.
La coordenada σ solo se define en el módulo 2π, y se considera mejor que varíe de -π a π, tomándola como el negativo del ángulo agudo F1 P F2 si P está en la mitad inferior del plano.
Las curvas de la constante σ corresponden a círculos no concéntricos que se cruzan en los dos focos.
La curva de τ = 0 se corresponde con el eje y (x = 0).
, que resulta Multiplicando esta ecuación por los complejos conjugados, se obtiene Empleando las identidades trigométricas para productos de senos y cosenos, se obtiene de lo que se deduce que Por lo tanto, los factores de escala para σ y τ son iguales, y dados por Muchos resultados desde este momento se deducen en rápida sucesión a partir de las fórmulas generales para las coordenadas ortogonales.
Por lo tanto, el elemento del área infinitesimal es igual a y el laplaciano viene dado por Las expresiones para
Un ejemplo es el campo eléctrico que rodea dos conductores cilíndricos paralelos con diámetros desiguales.
Los trazadores polares utilizan coordenadas bipolares para describir las rutas necesarias para dibujar una imagen dada.