Campo gravitatorio
Si se dispone en cierta región del espacio una masa
Este hecho se puede comprobar acercando otra masa
y constatando que se produce la interacción.
A la situación física que produce la masa
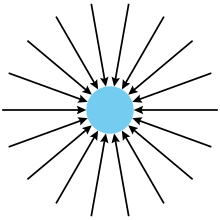
en un punto exterior a la esfera está dirigido hacia su centro y viene dado por la expresión: (1)
es la distancia del punto al centro de la esfera.
Esta ecuación (1), por la que el campo decrece según la ley de la inversa del cuadrado solo es válida para puntos exteriores a la esfera.
, crece linealmente desde cero en el centro de la esfera hasta su superficie, donde vale: (2)
creado por una distribución de masa totalmente general en un punto del espacio
El interés de describir la interacción gravitatoria mediante un campo radica en la posibilidad de expresar la interacción gravitacional como el producto de dos términos, uno que depende del valor local del campo
Por ejemplo, el movimiento de un planeta se puede describir como el movimiento orbital del planeta en presencia de un campo gravitatorio creado por el Sol.
La divergencia y el rotacional del campo gravitatorio valen: La primera nos indica que sus fuentes u orígenes son escalares (la masa) y el segundo nos indica que es conservativo.
Esa función escalar se denomina potencial gravitatorio y, en el caso del campo creado por una masa puntual (o una distribución esférica de masa) viene expresado por: De este modo, donde el signo negativo indica que el trabajo realizado por la fuerza gravitatoria representa una disminución del potencial gravitatorio.
Esto es, si la partícula se mueve en la dirección del campo, el trabajo que este realiza sobre ella es positivo y su potencial gravitatorio disminuye.
Así a cada punto del espacio se le puede asignar un potencial gravitatorio
relacionado con la densidad de la distribución de masa mediante su laplaciano y con el campo gravitatorio mediante su gradiente por: Una línea de fuerza o línea de campo, normalmente en el contexto del electromagnetismo, es la curva cuya tangente proporciona la dirección del campo en ese punto.
Suponen una forma útil de esquematizar gráficamente un campo, aunque son imaginarias y no tienen presencia física.
En la teoría de la relatividad general el campo gravitatorio no se describe como un campo de fuerzas, sino que las trayectorias curvas que los cuerpos siguen en el espacio tridimensional, son solo un reflejo de que el espacio-tiempo es curvo.
Por tanto, la curvatura de las trayectorias tridimensionales se debe a que la línea más recta posible en el espacio-tiempo de cuatro dimensiones no se proyecta como una recta, vista desde el espacio tridimensional.
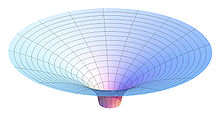
El campo gravitatorio se interpreta en relatividad como la curvatura del espacio-tiempo que, en presencia de materia, deja de ser plano.
Allí donde el espacio-tiempo no es plano, se percibe ese hecho como campo gravitatorio local, y viceversa, allí donde se percibe campo gravitatorio se tiene una geometría curva del espacio-tiempo.
Así, la teoría relativista de Einstein del campo gravitatorio es una teoría de la estructura geométrica local del espacio-tiempo.
Donde: Para campos gravitatorios débiles, que dan lugar a un espacio tiempo asintóticamente plano y cuerpos moviéndose en ellos a velocidades pequeñas comparadas con la velocidad de la luz (desde el punto de vista de los observadores estacionarios muy alejados de la fuente gravitatoria), puede representarse la geometría del espacio-tiempo curvo mediante una métrica muy cercana a al métrica euclídea dada por:
La primera de las anteriores implica que las coordenadas espaciales varían similarmente al caso clásico, aunque afectados por un factor de ralentización temporal
, mientras que la relación entre el tiempo propio y la coordenada temporal se obtiene integrando la segunda ecuación:
Sin embargo, en el caso de un espacio-tiempo estático es posible encontrar un análogo al potencial gravitatorio, que en el límite de campos débiles se reduce al potencial newtoniano.
A partir de la relación fundamental para la energía-momento, se tiene que:
Para campos débiles, esta última ecuación se puede reescribir, usando la aproximación that
Para el caso, un poco más general de un espacio-tiempo estacionario pueden usarse los dos potenciales de Hansen,[1] uno de los cuales desempeña un papel análogo al potencial newtoniano y el otro da el efecto gravitomagnético.
Si bien existe una ley local de conservación de la energía, no existe una magnitud global que pueda considerarse la energía del sistema, incluyendo el campo gravitatorio.