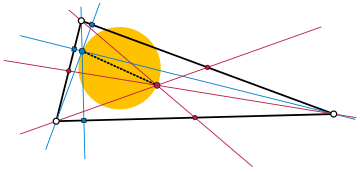
Círculo ortocentroidal

En geometría, el círculo ortocentroidal de un triángulo no equilátero es el círculo cuyo contorno pasa por el ortocentro del triángulo y por su centroide, situados en los extremos opuestos de un diámetro.Este diámetro también contiene el centro de nueve puntos del triángulo y pertenece a la recta de Euler, que también contiene el circuncentro, situado fuera del círculo ortocentroidal.Guinand demostró en 1984 que el incentro del triángulo debe estar en el interior del círculo ortocentroidal, pero no coincidiendo con el centro de nueve puntos; es decir, debe caer en el "disco ortocentroidal" abierto perforado en el centro de nueve puntos.451–452 El incentro puede ser cualquier punto del disco, dependiendo del triángulo específico que tenga ese círculo ortocentroidal particular.donde a, b y c son las longitudes de los lados del triángulo y D es el diámetro de su circunferencia circunscrita.