Algoritmo de Euclides
En matemáticas, el algoritmo de Euclides, o algoritmo euclidiano, es un método eficiente para calcular el máximo común divisor (MCD) de dos números enteros, el número más grande que los divide a ambos sin dejar resto.
Lleva el nombre del antiguo matemático griego Euclides, quien lo describió por primera vez en Elementos (ca.
La versión del algoritmo euclidiano descrita anteriormente (y por Euclides) puede requerir muchos pasos de resta para encontrar el MCD cuando uno de los números dados es mucho más grande que el otro.
Se desarrollaron métodos adicionales para mejorar la eficiencia del algoritmo en el siglo XX.
El algoritmo euclidiano se puede usar para resolver ecuaciones diofánticas, como encontrar números que satisfagan múltiples congruencias de acuerdo con el teorema chino del resto, para construir fracciones continuas y para encontrar aproximaciones racionales precisas a números reales.
En la concepción griega de la matemática, los números se entendían como magnitudes geométricas.
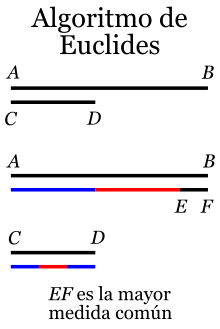
Euclides describe en la proposición I.2 en su Libro VII de sus Elementos un método que permite hallar la mayor medida común posible de dos números (segmentos) que no sean primos entre sí, aunque de acuerdo a la época tal método se explica en términos geométricos, lo que se ilustra en la siguiente transcripción.
Sean AB y CD los dos números que no son primos uno al otro.
Se necesita entonces encontrar la máxima medida común de AB y CD.
Pero si CD no mide a AB entonces algún número quedará de AB y CD, el menor siendo continuamente restado del mayor y que medirá al número que le precede.
En lenguaje moderno, el algoritmo se describe como sigue: El hecho de que los segmentos son conmesurables es clave para asegurar que el proceso termina tarde o temprano Al dividir
También es importante tener en cuenta que el máximo común divisor de cualquier número
Este mismo procedimiento se puede aplicar a cualesquiera dos números naturales.
En general, si se desea encontrar el máximo común divisor de dos números naturales
Aplicando estas reglas se obtiene la siguiente secuencia de operaciones: Como la sucesión de residuos va disminuyendo, al final un residuo tiene que ser cero y es en ese momento cuando el algoritmo termina.
Se puede expresar este algoritmo de manera más formal usando pseudocódigo.
pertenecientes a un dominio euclídeo Salida: Un máximo común divisor de
Supóngase que se utiliza el algoritmo de Euclides tradicional para calcular los valores
Esta propiedad no debería ser sorprendente, pues esta multiplicación de matrices equivale al método antes descrito donde se substituye cada ecuación en la anterior.
Utilizando el primer renglón de esta matriz se puede leer que
Para expresar el algoritmo de Euclides extendido es conveniente notar la manera en que se calculan los valores
Por lo tanto el algoritmo en pseudocódigo se puede expresar como sigue: Entrada: Valores
pertenecientes a un dominio euclídeo Salida: Un máximo común divisor de
(aunque también se puede generalizar para cualquier otro dominio euclídeo) si al dividirlos entre
Por ejemplo, 7 es congruente con 12 módulo 5 porque al dividir 7 entre 5 y 12 entre 5, en ambos casos obtenemos el mismo residuo (que es 2).
Más aún, si al usar el algoritmo de Euclides extendido (ahora con
Por ejemplo, si se desea calcular el máximo común divisor de
En términos de complejidad computacional, esto significa que se requieren
El número promedio de divisiones efectuadas por el algoritmo se estuvo investigando desde 1968, pero solo hasta apenas el año 2002, Brigitte Vallée demostró que si los dos números se pueden representar con
En general, los algoritmos 1 y 2 no son muy apropiados para implementarse directamente en un lenguaje de programación, especialmente porque consumen mucha memoria.