_(cropped).jpg/440px-Rye_Castle,_Rye,_East_Sussex,_England-6April2011_(1)_(cropped).jpg)
En geometría , un empaquetamiento de esferas es una disposición de esferas no superpuestas dentro de un espacio contenedor. Las esferas consideradas suelen ser todas de tamaño idéntico y el espacio suele ser un espacio euclidiano tridimensional . Sin embargo, los problemas de empaquetamiento de esferas se pueden generalizar para considerar esferas desiguales, espacios de otras dimensiones (donde el problema se convierte en empaquetamiento de círculos en dos dimensiones o empaquetamiento de hiperesferas en dimensiones superiores) o espacios no euclidianos como el espacio hiperbólico .
Un problema típico de empaquetamiento de esferas es encontrar una disposición en la que las esferas llenen la mayor parte posible del espacio. La proporción de espacio que llenan las esferas se denomina densidad de empaquetamiento de la disposición. Como la densidad local de un empaquetamiento en un espacio infinito puede variar según el volumen sobre el que se mide, el problema suele ser maximizar la densidad media o asintótica , medida sobre un volumen lo suficientemente grande.
Para esferas iguales en tres dimensiones, el empaquetamiento más denso utiliza aproximadamente el 74% del volumen. Un empaquetamiento aleatorio de esferas iguales generalmente tiene una densidad de alrededor del 63,5%. [1]
Una disposición reticular (comúnmente llamada disposición regular ) es aquella en la que los centros de las esferas forman un patrón muy simétrico que solo necesita n vectores para estar definidos de forma única (en un espacio euclidiano de n dimensiones ). Las disposiciones reticulares son periódicas. Las disposiciones en las que las esferas no forman una red (a menudo denominadas irregulares ) pueden ser periódicas, pero también aperiódicas (propiamente hablando, no periódicas ) o aleatorias . Debido a su alto grado de simetría , los empaquetamientos reticulares son más fáciles de clasificar que los no reticulares. Las redes periódicas siempre tienen densidades bien definidas.

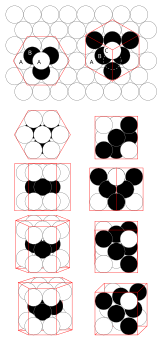

En el espacio euclidiano tridimensional, el empaquetamiento más denso de esferas iguales se logra mediante una familia de estructuras llamadas estructuras compactas . Un método para generar dicha estructura es el siguiente. Considere un plano con una disposición compacta de esferas sobre él. Llamémoslo A. Para tres esferas vecinas cualesquiera, se puede colocar una cuarta esfera encima en el hueco entre las tres esferas inferiores. Si hacemos esto para la mitad de los huecos en un segundo plano sobre el primero, creamos una nueva capa compacta. Hay dos opciones posibles para hacer esto, llamémoslas B y C. Supongamos que elegimos B. Entonces, la mitad de los huecos de B se encuentra sobre los centros de las bolas en A y la otra mitad se encuentra sobre los huecos de A que no se usaron para B. Por lo tanto, las bolas de una tercera capa se pueden colocar directamente sobre las bolas de la primera, produciendo una capa de tipo A, o sobre los huecos de la primera capa que no estaban ocupados por la segunda capa, produciendo una capa de tipo C. La combinación de capas de tipos A, B y C produce varias estructuras compactas.
Dos disposiciones simples dentro de la familia de empaquetamiento compacto corresponden a redes regulares. Una se llama empaquetamiento cúbico compacto (o cúbico centrado en las caras , "FCC"), donde las capas se alternan en la secuencia ABCABC... La otra se llama empaquetamiento hexagonal compacto ("HCP"), donde las capas se alternan en la secuencia ABAB... [ dudoso – discutir ] Pero son posibles muchas secuencias de apilamiento de capas (ABAC, ABCBA, ABCBAC, etc.), y aún así generan una estructura compacta. En todas estas disposiciones, cada esfera toca 12 esferas vecinas, [2] y la densidad promedio es
En 1611, Johannes Kepler conjeturó que esta es la máxima densidad posible entre los arreglos regulares e irregulares, lo que se conoció como la conjetura de Kepler . Carl Friedrich Gauss demostró en 1831 que estos empaquetamientos tienen la densidad más alta entre todos los empaquetamientos reticulares posibles. [3] En 1998, Thomas Callister Hales , siguiendo el enfoque sugerido por László Fejes Tóth en 1953, anunció una prueba de la conjetura de Kepler. La prueba de Hales es una prueba por agotamiento que implica la comprobación de muchos casos individuales mediante cálculos informáticos complejos. Los árbitros dijeron que estaban "99% seguros" de la exactitud de la prueba de Hales. El 10 de agosto de 2014, Hales anunció la finalización de una prueba formal utilizando la comprobación de pruebas automatizada , eliminando cualquier duda. [4]
En los sistemas físicos se encuentran a menudo otros empaquetamientos reticulares, entre ellos, el reticulado cúbico con una densidad de , el reticulado hexagonal con una densidad de y el reticulado tetraédrico con una densidad de . [5]
Los empaquetamientos en los que todas las esferas están limitadas por sus vecinas para permanecer en una posición se denominan rígidos o atascados . El empaquetamiento de esferas regular estrictamente atascado (mecánicamente estable incluso como un sistema finito) con la densidad más baja conocida es un cristal fcc diluido ("tunelizado") con una densidad de solo π √ 2 /9 ≈ 0,49365 . [6] El empaquetamiento atascado regular más suelto conocido tiene una densidad de aproximadamente 0,0555. [7]
Si intentamos construir una colección densamente empaquetada de esferas, nos sentiremos tentados a colocar siempre la siguiente esfera en un hueco entre tres esferas empaquetadas. Si se ensamblan cinco esferas de esta manera, serán consistentes con una de las disposiciones empaquetadas regularmente descritas anteriormente. Sin embargo, la sexta esfera colocada de esta manera hará que la estructura sea inconsistente con cualquier disposición regular. Esto da como resultado la posibilidad de un empaquetamiento aleatorio y cerrado de esferas que es estable frente a la compresión. [8] La vibración de un empaquetamiento aleatorio suelto puede dar como resultado la disposición de partículas esféricas en empaquetamientos regulares, un proceso conocido como cristalización granular . Tales procesos dependen de la geometría del recipiente que contiene los granos esféricos. [2]
Cuando se añaden esferas al azar a un contenedor y luego se comprimen, generalmente formarán lo que se conoce como una configuración de empaquetamiento "irregular" o "atascada" cuando ya no se las pueda comprimir más. Este empaquetamiento irregular generalmente tendrá una densidad de alrededor del 64%. Investigaciones recientes predicen analíticamente que no puede superar un límite de densidad del 63,4% [9]. Esta situación es diferente del caso de una o dos dimensiones, donde comprimir una colección de esferas unidimensionales o bidimensionales (es decir, segmentos de línea o círculos) producirá un empaquetamiento regular.
El problema del empaquetamiento de esferas es la versión tridimensional de una clase de problemas de empaquetamiento de esferas en dimensiones arbitrarias. En dos dimensiones, el problema equivalente es el empaquetamiento de círculos en un plano. En una dimensión, es el empaquetamiento de segmentos de línea en un universo lineal. [10]
En dimensiones superiores a tres, los empaquetamientos reticulares más densos de hiperesferas se conocen hasta en 8 dimensiones. [11] Se sabe muy poco sobre los empaquetamientos irregulares de hiperesferas; es posible que en algunas dimensiones el empaquetamiento más denso pueda ser irregular. Parte del apoyo a esta conjetura proviene del hecho de que en ciertas dimensiones (por ejemplo, 10) el empaquetamiento irregular más denso conocido es más denso que el empaquetamiento regular más denso conocido. [12]
En 2016, Maryna Viazovska anunció una prueba de que la red E 8 proporciona el empaquetamiento óptimo (independientemente de la regularidad) en el espacio de ocho dimensiones, [13] y poco después ella y un grupo de colaboradores anunciaron una prueba similar de que la red Leech es óptima en 24 dimensiones. [14] Este resultado se basó en métodos anteriores y los mejoró, los cuales mostraban que estas dos redes están muy cerca de ser óptimas. [15] Las nuevas pruebas implican el uso de la transformada de Laplace de una función modular cuidadosamente elegida para construir una función radialmente simétrica f tal que f y su transformada de Fourier f̂ sean ambas iguales a 1 en el origen , y ambas se anulen en todos los demás puntos de la red óptima, con f negativa fuera de la esfera central del empaquetamiento y f̂ positiva. Luego, se utiliza la fórmula de suma de Poisson para f para comparar la densidad de la red óptima con la de cualquier otro empaquetamiento. [16] Antes de que la prueba fuera formalmente arbitrada y publicada, el matemático Peter Sarnak calificó la prueba de "increíblemente simple" y escribió que "Simplemente empiezas a leer el artículo y sabes que es correcto". [17]
Otra línea de investigación en altas dimensiones está tratando de encontrar límites asintóticos para la densidad de los empaquetamientos más densos. Se sabe que para n grande , la red más densa en dimensión n tiene densidad entre cn ⋅ 2 − n (para alguna constante c ) y 2 −(0.599+o(1)) n . [18] Los límites conjeturales se encuentran en el medio. [19] En una preimpresión de 2023, Marcelo Campos, Matthew Jenssen, Marcus Michelen y Julian Sahasrabudhe mejoraron el límite inferior de la densidad máxima a , [20] [21] entre sus técnicas hacen uso del nibble de Rödl .

Muchos problemas en las ciencias químicas y físicas pueden relacionarse con problemas de empaquetamiento en los que se dispone de más de un tamaño de esfera. En este caso, existe la posibilidad de elegir entre separar las esferas en regiones de esferas iguales y compactas o combinar los distintos tamaños de esferas en un empaquetamiento compuesto o intersticial . Cuando se dispone de muchos tamaños de esferas (o una distribución ), el problema se vuelve rápidamente insoluble, pero se dispone de algunos estudios de esferas duras binarias (dos tamaños).
Cuando la segunda esfera es mucho más pequeña que la primera, es posible disponer las esferas grandes en una disposición compacta y luego disponer las esferas pequeñas dentro de los huecos octaédricos y tetraédricos. La densidad de este empaquetamiento intersticial depende sensiblemente de la relación de radios, pero en el límite de las relaciones de tamaño extremas, las esferas más pequeñas pueden llenar los huecos con la misma densidad que las esferas más grandes llenaron el espacio. [23] Incluso si las esferas grandes no están en una disposición compacta, siempre es posible insertar algunas esferas más pequeñas de hasta 0,29099 del radio de la esfera más grande. [24]
Cuando la esfera más pequeña tiene un radio mayor que 0,41421 veces el radio de la esfera más grande, ya no es posible que encaje ni siquiera en los agujeros octaédricos de la estructura compacta. Por lo tanto, más allá de este punto, la estructura anfitriona debe expandirse para acomodar los intersticiales (lo que compromete la densidad general) o reorganizarse en una estructura compuesta cristalina más compleja. Se conocen estructuras que superan la densidad de empaquetamiento compacto para proporciones de radio de hasta 0,659786. [22] [25]
También se han obtenido límites superiores para la densidad que se pueden obtener en tales empaquetamientos binarios. [26]
En muchas situaciones químicas, como los cristales iónicos , la estequiometría está limitada por las cargas de los iones constituyentes. Esta restricción adicional en el empaquetamiento, junto con la necesidad de minimizar la energía de Coulomb de las cargas que interactúan, conduce a una diversidad de disposiciones de empaquetamiento óptimas.
El límite superior para la densidad de un empaquetamiento de esferas estrictamente atascado con cualquier conjunto de radios es 1; un ejemplo de tal empaquetamiento de esferas es el empaquetamiento de esferas apolíneo. El límite inferior para tal empaquetamiento de esferas es 0; un ejemplo es el empaquetamiento de esferas dionisíaco. [27]
Aunque el concepto de círculos y esferas se puede extender al espacio hiperbólico , encontrar el empaquetamiento más denso se vuelve mucho más difícil. En un espacio hiperbólico no hay límite para el número de esferas que pueden rodear a otra esfera (por ejemplo, los círculos de Ford pueden considerarse como una disposición de círculos hiperbólicos idénticos en la que cada círculo está rodeado por un número infinito de otros círculos). El concepto de densidad media también se vuelve mucho más difícil de definir con precisión. Los empaquetamientos más densos en cualquier espacio hiperbólico son casi siempre irregulares. [28]
A pesar de esta dificultad, K. Böröczky proporciona un límite superior universal para la densidad de empaquetamientos de esferas del espacio n hiperbólico donde n ≥ 2. [29] En tres dimensiones, el límite de Böröczky es aproximadamente 85,327613%, y se realiza mediante el empaquetamiento de la horósfera del panal tetraédrico de orden 6 con el símbolo de Schläfli {3,3,6}. [30] Además de esta configuración, se sabe que existen al menos otros tres empaquetamientos de la horósfera en el espacio 3 hiperbólico que realizan el límite superior de densidad. [31]
El gráfico de contacto de un empaquetamiento finito arbitrario de bolas unitarias es el gráfico cuyos vértices corresponden a los elementos del empaquetamiento y cuyos dos vértices están conectados por una arista si los dos elementos del empaquetamiento correspondientes se tocan entre sí. La cardinalidad del conjunto de aristas del gráfico de contacto da el número de pares en contacto, el número de 3-ciclos en el gráfico de contacto da el número de tripletes en contacto, y el número de tetraedros en el gráfico de contacto da el número de cuádruples en contacto (en general, para un gráfico de contacto asociado con un empaquetamiento de esferas en n dimensiones, la cardinalidad del conjunto de n -símplices en el gráfico de contacto da el número de ( n + 1)-tuplas en contacto en el empaquetamiento de esferas). En el caso del espacio euclidiano tridimensional, Karoly Bezdek y Samuel Reid en la Universidad de Calgary demostraron límites superiores no triviales para el número de pares, tripletes y cuádruples en contacto [32] .
El problema de encontrar la disposición de n esferas idénticas que maximice el número de puntos de contacto entre las esferas se conoce como el "problema de la esfera pegajosa". El máximo se conoce para n ≤ 11, y solo se conocen valores conjeturales para n mayores . [33]
El empaquetamiento de esferas en las esquinas de un hipercubo (con las esferas definidas por la distancia de Hamming ) corresponde al diseño de códigos de corrección de errores : si las esferas tienen un radio t , entonces sus centros son palabras de código de un código de corrección de errores (2 t + 1). Los empaquetamientos reticulares corresponden a códigos lineales. Existen otras relaciones más sutiles entre el empaquetamiento de esferas euclidiano y los códigos de corrección de errores. Por ejemplo, el código binario de Golay está estrechamente relacionado con la red Leech de 24 dimensiones.
Para más detalles sobre estas conexiones, véase el libro Sphere Packings, Lattices and Groups de Conway y Sloane . [34]