Línea mundial

Trayectoria única de un objeto a medida que viaja a través del espacio-tiempo

La línea de universo (o worldline ) de un objeto es la trayectoria que sigue un objeto en el espacio-tiempo de cuatro dimensiones . Es un concepto importante de la física moderna , y en particular de la física teórica .

El concepto de "línea mundial" se distingue de conceptos como " órbita " o " trayectoria " (por ejemplo, la órbita de un planeta en el espacio o la trayectoria de un automóvil en una carretera) por la inclusión de la dimensión tiempo , y típicamente abarca una gran área de espacio-tiempo en donde las trayectorias que son rectas perceptualmente se representan como curvas en el espacio-tiempo para mostrar sus estados de posición ( relativamente ) más absolutos, para revelar la naturaleza de la relatividad especial o las interacciones gravitacionales .

La idea de las líneas del universo fue originada por físicos y fue desarrollada por Hermann Minkowski . El término se utiliza ahora con mayor frecuencia en el contexto de las teorías de la relatividad (es decir, la relatividad especial y la relatividad general ).

Uso en física

Una línea de universo de un objeto (generalmente aproximada como un punto en el espacio, por ejemplo, una partícula o un observador) es la secuencia de eventos del espacio-tiempo correspondientes a la historia del objeto. Una línea de universo es un tipo especial de curva en el espacio-tiempo. A continuación se explicará una definición equivalente: Una línea de universo es una curva nula o similar al tiempo en el espacio-tiempo. Cada punto de una línea de universo es un evento que se puede etiquetar con el tiempo y la posición espacial del objeto en ese momento.

Por ejemplo, la órbita de la Tierra en el espacio es aproximadamente un círculo, una curva tridimensional (cerrada) en el espacio: la Tierra regresa cada año al mismo punto en el espacio con respecto al Sol. Sin embargo, llega allí en un momento diferente (más tarde). La línea del universo de la Tierra es, por lo tanto, helicoidal en el espacio-tiempo (una curva en un espacio de cuatro dimensiones) y no regresa al mismo punto.

El espacio-tiempo es la colección de eventos , junto con un sistema de coordenadas continuo y uniforme que identifica los eventos. Cada evento puede etiquetarse con cuatro números: una coordenada de tiempo y tres coordenadas espaciales; por lo tanto, el espacio-tiempo es un espacio de cuatro dimensiones. El término matemático para el espacio-tiempo es una variedad de cuatro dimensiones (un espacio topológico que se asemeja localmente al espacio euclidiano cerca de cada punto). El concepto también se puede aplicar a un espacio de dimensiones superiores. Para facilitar la visualización de cuatro dimensiones, a menudo se suprimen dos coordenadas espaciales. Un evento se representa entonces mediante un punto en un diagrama de Minkowski , que es un plano generalmente trazado con la coordenada de tiempo, digamos , verticalmente, y la coordenada espacial, digamos , horizontalmente. Como lo expresó FR Harvey ${\displaystyle t}$ ${\displaystyle x}$

Una curva M en [el espacio-tiempo] se denomina línea de universo de una partícula si su tangente es similar a un tiempo futuro en cada punto. El parámetro de longitud de arco se denomina tiempo propio y generalmente se denota τ. La longitud de M se denomina tiempo propio de la partícula. Si la línea de universo M es un segmento de línea, entonces se dice que la partícula está en caída libre . ^{[1] : 62–63}

Una línea de universo traza la trayectoria de un único punto en el espacio-tiempo. Una lámina de universo es la superficie bidimensional análoga trazada por una línea unidimensional (como una cuerda) que viaja a través del espacio-tiempo. La lámina de universo de una cuerda abierta (con extremos sueltos) es una tira; la de una cuerda cerrada (un bucle) se parece a un tubo.

Una vez que el objeto no se aproxima a un mero punto sino que tiene un volumen extendido, traza no una línea de mundo sino más bien un tubo de mundo.

Las líneas del mundo como método para describir acontecimientos

Línea del mundo, hoja del mundo y volumen del mundo, tal como se derivan de partículas , cuerdas y branas .

Una línea o curva unidimensional se puede representar mediante las coordenadas en función de un parámetro. Cada valor del parámetro corresponde a un punto en el espacio-tiempo y al variar el parámetro se traza una línea. Por lo tanto, en términos matemáticos, una curva se define mediante cuatro funciones de coordenadas (donde normalmente denota la coordenada temporal) que dependen de un parámetro . Una cuadrícula de coordenadas en el espacio-tiempo es el conjunto de curvas que se obtiene si tres de las cuatro funciones de coordenadas se establecen en una constante. ${\displaystyle x^{a}(\tau ),\;a=0,1,2,3}$ ${\displaystyle x^{0}}$ ${\displaystyle \tau }$

A veces, el término línea de universo se utiliza de manera informal para cualquier curva en el espacio-tiempo. Esta terminología causa confusión. Más propiamente, una línea de universo es una curva en el espacio-tiempo que traza la historia (temporal) de una partícula, un observador o un objeto pequeño. Por lo general, se utiliza el tiempo propio de un objeto o de un observador como parámetro de curva a lo largo de la línea de universo. ${\displaystyle \tau }$

Ejemplos triviales de curvas del espacio-tiempo

Tres líneas mundiales diferentes que representan viajes a diferentes velocidades constantes. t es el tiempo y x la distancia.

Una curva que consiste en un segmento de línea horizontal (una línea en un tiempo de coordenadas constante) puede representar una varilla en el espacio-tiempo y no sería una línea de universo en el sentido propio. El parámetro simplemente traza la longitud de la varilla.

Una línea con coordenadas espaciales constantes (una línea vertical utilizando la convención adoptada anteriormente) puede representar una partícula en reposo (o un observador estacionario). Una línea inclinada representa una partícula con una velocidad de coordenadas constantes (cambio constante en la coordenada espacial a medida que aumenta la coordenada temporal). Cuanto más inclinada esté la línea con respecto a la vertical, mayor será la velocidad.

Dos líneas de universo que comienzan por separado y luego se cruzan significan una colisión o un "encuentro". Dos líneas de universo que comienzan en el mismo evento en el espacio-tiempo y luego siguen su propio camino pueden representar, por ejemplo, la descomposición de una partícula en otras dos o la emisión de una partícula por otra.

Las líneas del mundo de una partícula y un observador pueden estar interconectadas con la línea del mundo de un fotón (la trayectoria de la luz) y formar un diagrama que representa la emisión de un fotón por una partícula que posteriormente es observada por el observador (o absorbida por otra partícula).

Vector tangente a una línea del mundo: cuatro velocidades

Las cuatro funciones de coordenadas que definen una línea del universo son funciones de números reales de una variable real y pueden diferenciarse simplemente mediante el cálculo habitual. Sin la existencia de una métrica (esto es importante darse cuenta) uno puede imaginar la diferencia entre un punto en la curva en el valor del parámetro y un punto en la curva un poco (parámetro ) más alejado. En el límite , esta diferencia dividida por define un vector, el vector tangente de la línea del universo en el punto . Es un vector de cuatro dimensiones, definido en el punto . Está asociado con la velocidad tridimensional normal del objeto (pero no es lo mismo) y por lo tanto se denomina velocidad de cuatro dimensiones o en componentes: ${\displaystyle x^{a}(\tau ),\;a=0,1,2,3}$ ${\displaystyle \tau }$ ${\displaystyle p}$ ${\displaystyle \tau _{0}}$ ${\displaystyle \tau _{0}+\Delta \tau }$ ${\displaystyle \Delta \tau \to 0}$ ${\displaystyle \Delta \tau }$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle {\vec {v}}}$ $${\displaystyle {\vec {v}}=\left(v^{0},v^{1},v^{2},v^{3}\right)=\left({\frac {dx^{0}}{d\tau }}\;,{\frac {dx^{1}}{d\tau }}\;,{\frac {dx^{2}}{d\tau }}\;,{\frac {dx^{3}}{d\tau }}\right)}$$

de modo que las derivadas se toman en el punto , por lo tanto en . ${\displaystyle p}$ ${\displaystyle \tau =\tau _{0}}$

Todas las curvas que pasan por el punto p tienen un vector tangente, no solo las líneas universales. La suma de dos vectores es nuevamente un vector tangente a alguna otra curva y lo mismo sucede con la multiplicación por un escalar. Por lo tanto, todos los vectores tangentes para un punto p abarcan un espacio lineal , denominado espacio tangente en el punto p. Por ejemplo, tomando un espacio bidimensional, como la superficie (curva) de la Tierra, su espacio tangente en un punto específico sería la aproximación plana del espacio curvo.

Líneas del mundo en la relatividad especial

Hasta ahora, una línea de universo (y el concepto de vectores tangentes) se ha descrito sin un medio para cuantificar el intervalo entre eventos. Las matemáticas básicas son las siguientes: La teoría de la relatividad especial impone algunas restricciones a las posibles líneas de universo. En la relatividad especial, la descripción del espacio-tiempo se limita a sistemas de coordenadas especiales que no aceleran (y, por lo tanto, tampoco rotan), denominados sistemas de coordenadas inerciales . En tales sistemas de coordenadas, la velocidad de la luz es una constante. La estructura del espacio-tiempo está determinada por una forma bilineal η, que da un número real para cada par de eventos. La forma bilineal a veces se denomina métrica del espacio-tiempo , pero dado que los eventos distintos a veces dan como resultado un valor cero, a diferencia de las métricas en los espacios métricos de las matemáticas, la forma bilineal no es una métrica matemática del espacio-tiempo.

Las líneas de universo de partículas u objetos en caída libre se denominan geodésicas . En la relatividad especial, son líneas rectas en el espacio de Minkowski .

A menudo, las unidades de tiempo se eligen de forma que la velocidad de la luz se represente mediante líneas que forman un ángulo fijo, normalmente de 45 grados, formando un cono con el eje vertical (el del tiempo). En general, las curvas útiles en el espacio-tiempo pueden ser de tres tipos (los otros tipos serían en parte de uno y en parte de otro):

• Curvas que semejan luces y que tienen en cada punto la velocidad de la luz. Forman un cono en el espacio-tiempo, dividiéndolo en dos partes. El cono es tridimensional en el espacio-tiempo, aparece como una línea en los dibujos en los que se suprimen dos dimensiones y como un cono en los dibujos en los que se suprime una dimensión espacial.

Ejemplo de cono de luz , la superficie tridimensional de todos los posibles rayos de luz que llegan a un punto del espacio-tiempo y parten de él. Aquí se representa con una dimensión espacial suprimida.

Los sistemas inerciales que se mueven en paralelo momentáneamente a lo largo de la trayectoria ("línea del mundo") de un observador que acelera rápidamente (centro). La dirección vertical indica el tiempo, mientras que la horizontal indica la distancia; la línea discontinua es el espacio-tiempo del observador. Los puntos pequeños son eventos específicos en el espacio-tiempo. Observe cómo cambia el sistema inercial que se mueve en paralelo momentáneamente cuando el observador acelera.

• Curvas temporales , con una velocidad menor que la de la luz. Estas curvas deben estar dentro de un cono definido por curvas similares a la luz. En nuestra definición anterior: las líneas del universo son curvas temporales en el espacio-tiempo .
• Curvas de tipo espacial que caen fuera del cono de luz. Tales curvas pueden describir, por ejemplo, la longitud de un objeto físico. La circunferencia de un cilindro y la longitud de una varilla son curvas de tipo espacial.

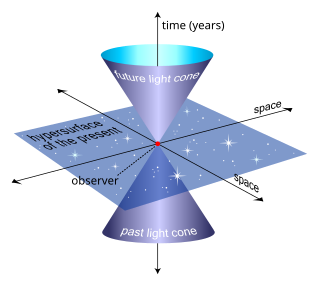
En un evento dado en una línea del mundo, el espacio-tiempo ( espacio de Minkowski ) se divide en tres partes.

• El futuro del evento dado está formado por todos los eventos a los que se puede llegar a través de curvas temporales que se encuentran dentro del cono de luz futuro.
• El pasado del evento dado está formado por todos los eventos que pueden influir en el evento (es decir, que pueden conectarse mediante líneas del mundo dentro del cono de luz del pasado al evento dado).
  • El cono de luz en el evento dado está formado por todos los eventos que pueden conectarse a través de rayos de luz con el evento. Cuando observamos el cielo por la noche, básicamente solo vemos el cono de luz pasado dentro de todo el espacio-tiempo.
• El otro lugar es la región entre los dos conos de luz. Los puntos en el otro lugar del observador son inaccesibles para él; sólo los puntos del pasado pueden enviar señales al observador. En la experiencia ordinaria de laboratorio, utilizando unidades y métodos de medición comunes, puede parecer que miramos el presente, pero de hecho siempre hay un tiempo de retraso para que la luz se propague. Por ejemplo, vemos el Sol como era hace unos 8 minutos, no como es "ahora mismo". A diferencia del presente en la teoría galileana/newtoniana, el otro lugar es espeso; no es un volumen tridimensional sino una región espacio-temporal de cuatro dimensiones.
  • En "otro lugar" se incluye el hiperplano simultáneo , que se define para un observador dado por un espacio que es hiperbólico-ortogonal a su línea de universo. En realidad es tridimensional, aunque sería un plano bidimensional en el diagrama porque tuvimos que descartar una dimensión para hacer una imagen inteligible. Aunque los conos de luz son los mismos para todos los observadores en un evento espacio-temporal dado, diferentes observadores, con diferentes velocidades pero coincidentes en el evento (punto) en el espacio-tiempo, tienen líneas de universo que se cruzan entre sí en un ángulo determinado por sus velocidades relativas y, por lo tanto, tienen diferentes hiperplanos simultáneos.
  • El presente a menudo significa el único evento espaciotemporal que se está considerando.

Hiperplano simultáneo

Dado que una línea de universo determina un 4-vector de velocidad que es similar al tiempo, la forma de Minkowski determina una función lineal mediante Sea N el espacio nulo de esta funcional lineal. Entonces, N se llama hiperplano simultáneo con respecto a v . La relatividad de la simultaneidad es una afirmación de que N depende de v . De hecho, N es el complemento ortogonal de v con respecto a η. Cuando dos líneas de universo u y w están relacionadas, entonces comparten el mismo hiperplano simultáneo. Este hiperplano existe matemáticamente, pero las relaciones físicas en relatividad involucran el movimiento de información por la luz. Por ejemplo, la fuerza electrostática tradicional descrita por la ley de Coulomb puede representarse en un hiperplano simultáneo, pero las relaciones relativistas de carga y fuerza involucran potenciales retardados . ${\displaystyle w(\tau )\in R^{4}}$ ${\displaystyle v={\frac {dw}{d\tau }}}$ ${\displaystyle \eta (v,x)}$ ${\displaystyle R^{4}\rightarrow R}$ ${\displaystyle x\mapsto \eta (v,x).}$ ${\displaystyle {\frac {du}{d\tau }}={\frac {dw}{d\tau }},}$

Líneas del mundo en la relatividad general

El uso de líneas de universo en la relatividad general es básicamente el mismo que en la relatividad especial , con la diferencia de que el espacio-tiempo puede ser curvado . Existe una métrica y su dinámica está determinada por las ecuaciones de campo de Einstein y depende de la distribución de masa-energía en el espacio-tiempo. Nuevamente, la métrica define curvas similares a la luz (nulas), similares al espacio y similares al tiempo . Además, en la relatividad general, las líneas de universo incluyen curvas similares al tiempo y curvas nulas en el espacio-tiempo, donde las curvas similares al tiempo caen dentro del cono de luz. Sin embargo, un cono de luz no está necesariamente inclinado a 45 grados con respecto al eje del tiempo. Sin embargo, esto es un artefacto del sistema de coordenadas elegido y refleja la libertad de coordenadas ( invariancia del difeomorfismo ) de la relatividad general. Cualquier curva similar al tiempo admite un observador comóvil cuyo "eje del tiempo" corresponde a esa curva y, dado que ningún observador es privilegiado, siempre podemos encontrar un sistema de coordenadas local en el que los conos de luz estén inclinados a 45 grados con respecto al eje del tiempo. Véase también, por ejemplo, las coordenadas de Eddington-Finkelstein .

Las líneas del mundo de partículas u objetos en caída libre (como planetas alrededor del Sol o un astronauta en el espacio) se denominan geodésicas .

Líneas del mundo en la teoría cuántica de campos

La teoría cuántica de campos, el marco en el que se describe toda la física de partículas moderna, suele describirse como una teoría de campos cuantizados. Sin embargo, aunque no se aprecia ampliamente, se sabe desde Feynman ^[2] que muchas teorías cuánticas de campos pueden describirse de manera equivalente en términos de líneas de universo. Esto precedió a gran parte de su trabajo ^[3] sobre la formulación que luego se volvió más estándar. La formulación de la línea de universo de la teoría cuántica de campos ha demostrado ser particularmente fructífera para varios cálculos en teorías de calibración ^{[4] [5] [6]} y en la descripción de los efectos no lineales de los campos electromagnéticos. ^{[7] [8]}

Líneas del mundo en la literatura

En 1884, C. H. Hinton escribió un ensayo titulado "¿Qué es la cuarta dimensión?", que publicó como novela científica .

¿Por qué, entonces, no deberíamos ser los seres de cuatro dimensiones nosotros mismos, y nuestros estados sucesivos su paso a través del espacio tridimensional al que está confinada nuestra conciencia? ^{[9] : 18–19}

En los primeros tiempos de la relatividad, J. C. Fields, de la Universidad de Toronto, dio una descripción popular de las líneas del mundo humano . Según lo describió el abogado de Toronto Norman Robertson:

Recuerdo que [Fields] daba una conferencia en una de las tardes de los sábados en el Real Instituto Canadiense . Se anunciaba que se trataba de una "fantasía matemática", ¡y lo era! La esencia del ejercicio era la siguiente: postuló que, a partir de su nacimiento, cada ser humano tenía una especie de aura espiritual con un largo filamento o hilo adherido, que viajaba detrás de él durante toda su vida. Luego procedió a describir en su imaginación el complicado enredo en el que cada individuo se veía envuelto en su relación con otros individuos, comparando los simples enredos de la juventud con esos complicados nudos que se desarrollan en la vida posterior. ^[10]

Kurt Vonnegut, en su novela Matadero Cinco , describe las líneas de mundo de las estrellas y las personas:

“Billy Pilgrim dice que el Universo no parece un montón de puntitos brillantes para las criaturas de Tralfamadore. Las criaturas pueden ver dónde ha estado cada estrella y hacia dónde va, de modo que los cielos están llenos de espaguetis luminosos y enrarecidos. Y los tralfamadorianos tampoco ven a los seres humanos como criaturas de dos piernas. Los ven como grandes milpiés, "con piernas de bebé en un extremo y piernas de anciano en el otro", dice Billy Pilgrim.”

Casi todas las historias de ciencia ficción que utilizan este concepto de forma activa, como para permitir el viaje en el tiempo , simplifican excesivamente este concepto a una línea de tiempo unidimensional para que se ajuste a una estructura lineal, que no se ajusta a los modelos de la realidad. Estas máquinas del tiempo suelen representarse como instantáneas, con su contenido que sale en un momento y llega en otro, pero en el mismo punto geográfico literal en el espacio. Esto se lleva a cabo a menudo sin tener en cuenta un marco de referencia, o con la suposición implícita de que el marco de referencia es local; como tal, esto requeriría una teletransportación precisa, ya que un planeta en rotación, al estar bajo aceleración, no es un marco inercial, o que la máquina del tiempo permanezca en el mismo lugar, con su contenido "congelado".

El autor Oliver Franklin publicó en 2008 una obra de ciencia ficción titulada World Lines en la que relata una explicación simplificada de la hipótesis para los profanos. ^[11]

En el cuento Life-Line , el autor Robert A. Heinlein describe la línea del mundo de una persona: ^[12]

Se acercó a uno de los periodistas y le dijo: "Supongamos que te tomamos como ejemplo. Te llamas Rogers, ¿no es así? Muy bien, Rogers, eres un acontecimiento espacio-temporal que tiene una duración de cuatro maneras. No mides ni un metro ochenta de alto, tienes unos cincuenta centímetros de ancho y quizá unos veinticinco de grosor. En el tiempo, detrás de ti se extiende más de este acontecimiento espacio-temporal, que llega quizá hasta el año 196, del que vemos aquí una sección transversal en ángulo recto con el eje del tiempo, y tan gruesa como el presente. En el otro extremo hay un bebé que huele a leche agria y babea el desayuno en su babero. En el otro extremo yace, quizá, un anciano de algún lugar de los años ochenta.

"Imaginemos este acontecimiento espacio-temporal que llamamos Rogers como un largo gusano rosado, continuo a través de los años, un extremo en el vientre de su madre y el otro en la tumba..."

El término se utiliza en Los hijos de Matusalén de Heinlein , al igual que en El quincunce del tiempo de James Blish (ampliado a partir de "Beep").

Una novela visual llamada Steins;Gate , producida por 5pb. , cuenta una historia basada en el cambio de líneas de mundo. Steins;Gate es parte de la serie " Science Adventure ". Las líneas de mundo y otros conceptos físicos como el Mar de Dirac también se utilizan a lo largo de la serie.

La novela Anathem de Neal Stephenson implica una larga discusión sobre líneas de mundo durante una cena en medio de un debate filosófico entre el realismo platónico y el nominalismo .

Absolute Choice representa diferentes líneas de mundo como una subtrama y un dispositivo de ambientación.

Una armada espacial que intenta completar un camino temporal (casi) cerrado como maniobra estratégica constituye el telón de fondo y el principal recurso argumental de "Singularity Sky" de Charles Stross .

Véase también

• Tipos específicos de líneas mundiales
  • Geodésicas
  • Curvas temporales cerradas
  • Estructura causal , curvas que representan una variedad de diferentes tipos de líneas del mundo.
  • Línea isotrópica
• Diagrama de Feynman
• Geografía del tiempo

Referencias

1. Harvey, F. Reese (1990). Sección "Relatividad especial" del capítulo "Espacios vectoriales euclidianos/lorentzianos". Spinors and Calibrations . Academic Press . págs. 62–67. ISBN 9780080918631.
2. Feynman, Richard P. (1950). "Formulación matemática de la teoría cuántica de la interacción electromagnética". Physical Review . 80 (1): 108–128. doi :10.1103/PhysRev.80.440.
3. Feynman, Richard P. (1951). "Un cálculo de operadores con aplicaciones en la electrodinámica cuántica" (PDF) . Physical Review . 84 (3): 440–457. Bibcode :1951PhRv...84..108F. doi :10.1103/PhysRev.84.108.
4. Bern, Zvi ; Kosower, David A. (1991). "Cálculo eficiente de amplitudes de QCD de un bucle". Physical Review Letters . 66 (13): 1669–1672. Bibcode :1991PhRvL..66.1669B. doi :10.1103/PhysRevLett.66.1669. PMID  10043277.
5. Bern, Zvi ; Dixon, Lance ; Kosower, David A. (1996). "Progreso en los cálculos de QCD de un bucle" (PDF) . Revisión anual de la ciencia nuclear y de partículas . 46 : 109–148. arXiv : hep-ph/9602280 . Código Bibliográfico :1996ARNPS..46..109B. doi : 10.1146/annurev.nucl.46.1.109 .
6. Schubert, Christian (2001). "Teoría cuántica de campos perturbativa en el formalismo inspirado en cuerdas". Physics Reports . 355 (2–3): 73–234. arXiv : hep-th/0101036 . Código Bibliográfico :2001PhR...355...73S. doi :10.1016/S0370-1573(01)00013-8. S2CID  118891361.
7. Affleck, Ian K. ; Alvarez, Orlando; Manton, Nicholas S. (1982). "Producción de pares en acoplamiento fuerte en campos externos débiles". Física nuclear B . 197 (3): 509–519. Código Bibliográfico :1982NuPhB.197..509A. doi :10.1016/0550-3213(82)90455-2.
8. Dunne, Gerald V.; Schubert, Christian (2005). "Instantones de línea de mundo y producción de pares en campos no homogéneos" (PDF) . Physical Review D . 72 (10): 105004. arXiv : hep-th/0507174 . Bibcode :2005PhRvD..72j5004D. doi :10.1103/PhysRevD.72.105004. S2CID  119357180.
9. Hinton, CH (1884). "¿Qué es la cuarta dimensión?". Romances científicos: Primera serie . S. Sonnenschein . págs. 1–32.
10. Robinson, Gilbert de Beauregard (1979). El Departamento de Matemáticas de la Universidad de Toronto, 1827-1978 . University of Toronto Press . pág. 19. ISBN. 0-7727-1600-5.
11. Oliver Franklin (2008). Líneas del mundo . Epic Press. ISBN 978-1-906557-00-3.
12. "Technovelgy: Chronovitameter" . Consultado el 8 de septiembre de 2010 .

• Minkowski, Hermann (1909), "Raum und Zeit"  , Physikalische Zeitschrift , 10 : 75–88

• Varias traducciones al inglés en Wikisource: Espacio y tiempo

• Ludwik Silberstein (1914) Teoría de la relatividad , pág. 130, Macmillan and Company .

Enlaces externos

• Artículo sobre líneas del mundo en h2g2 .

• Texto detallado sobre las líneas del mundo y la relatividad especial.