Transformación afín

En geometría euclidiana , una transformación afín o afinidad (del latín, affinis , "conectado con") es una transformación geométrica que preserva las líneas y el paralelismo , pero no necesariamente las distancias y los ángulos euclidianos .

En términos más generales, una transformación afín es un automorfismo de un espacio afín (los espacios euclidianos son espacios afines específicos), es decir, una función que proyecta un espacio afín sobre sí mismo mientras preserva tanto la dimensión de cualquier subespacio afín (lo que significa que envía puntos a puntos, líneas a líneas, planos a planos, etc.) como las razones de las longitudes de los segmentos de línea paralelos . En consecuencia, los conjuntos de subespacios afines paralelos permanecen paralelos después de una transformación afín. Una transformación afín no necesariamente preserva los ángulos entre líneas o las distancias entre puntos, aunque sí preserva las razones de las distancias entre puntos que se encuentran en una línea recta.

Si $X$ es el conjunto de puntos de un espacio afín, entonces cada transformación afín en $X$ puede representarse como la composición de una transformación lineal en $X$ y una traslación de $X.$ A diferencia de una transformación puramente lineal, una transformación afín no necesita conservar el origen del espacio afín. Por lo tanto, toda transformación lineal es afín, pero no toda transformación afín es lineal.

Los ejemplos de transformaciones afines incluyen traducción, escala , homotecia , similitud , reflexión , rotación , rotación hiperbólica , mapeo de corte y composiciones de ellas en cualquier combinación y secuencia.

Considerando un espacio afín como el complemento de un hiperplano en el infinito de un espacio proyectivo , las transformaciones afines son las transformaciones proyectivas de ese espacio proyectivo que dejan al hiperplano en el infinito invariante , restringido al complemento de ese hiperplano.

Una generalización de una transformación afín es una función afín ^[1] (o homomorfismo afín o función afín ) entre dos espacios afines (potencialmente diferentes) sobre el mismo cuerpo $k$ . Sean $(X, V, k)$ y $(Z, W, k)$ dos espacios afines con $X$ y $Z$ los conjuntos de puntos y $V$ y $W los$ espacios vectoriales asociados respectivos sobre el cuerpo $k$ . Una función $f : X \to Z$ es una función afín si existe una función lineal $m f : V \to W$ tal que $m f (x - y) = f (x) - f (y)$ para todo $x, y$ en $X.$ ^[2 ]

Definición

Sea $X$ un espacio afín sobre un cuerpo $k$ y $V$ su espacio vectorial asociado. Una transformación afín es una biyección $f$ de $X$ sobre sí misma que es una función afín ; esto significa que una función lineal $g$ de $V$ a $V$ está bien definida por la ecuación. Aquí, como es habitual, la resta de dos puntos denota el vector libre del segundo punto al primero, y " bien definido " significa que implica que $g(yx)=f(y)-f(x);$ $yx=y'-x'$ $f(y)-f(x)=f(y')-f(x').$

Si la dimensión de $X$ es al menos dos, una transformación semiafín $f$ de $X$ es una biyección de $X$ sobre sí mismo que satisface: ^[3]

Para cada subespacio afín $d$ -dimensional $S$ de $X$ , entonces $f$ $($ $S$ $)$ es también un subespacio afín $d$ $-dimensional de X$ .
Si $S$ y $T$ son subespacios afines paralelos de $X$ , entonces $f (S)$ y $f (T)$ son paralelos.

Estas dos condiciones se satisfacen mediante transformaciones afines y expresan precisamente lo que se quiere decir con la expresión de que " $f$ preserva el paralelismo".

Estas condiciones no son independientes ya que la segunda se sigue de la primera. ^[4] Además, si el campo $k$ tiene al menos tres elementos, la primera condición se puede simplificar a: $f$ es una colineación , es decir, asigna líneas a líneas. ^[5]

Estructura

Por la definición de un espacio afín, $V$ actúa sobre $X$ , de modo que, para cada par en $X$ $\times$ $V$ hay asociado un punto $y$ en $X$ . Podemos denotar esta acción por . Aquí usamos la convención de que son dos notaciones intercambiables para un elemento de $V$ . Al fijar un punto $c$ en $X$ se puede definir una función $m$ $c$ $:$ $X$ $\to$ $V$ por $m$ $c$ $($ $x$ $) =$ $cx$ $\to$ . Para cualquier $c$ , esta función es biyectiva, y por lo tanto, tiene una función inversa $m$ $c$ $-1$ $:$ $V$ $\to$ $X$ dada por . Estas funciones se pueden usar para convertir $X$ en un espacio vectorial (con respecto al punto $c$ ) definiendo: ^[6] $(x,\mathbf {v})$ ${\vec {v}}(x)=y$ ${\vec {v}}={\textbf {v}}$ $m_{c}^{-1}({\textbf {v}})={\vec {v}}(c)$

$x+y=m_{c}^{-1}\left(m_{c}(x)+m_{c}(y)\right),{\text{ para todo }}x,y{\text{ en }}X,$ y
$rx=m_{c}^{-1}\left(rm_{c}(x)\right),{\text{ para todos }}r{\text{ en }}k{\text{ y }}x{\text{ en }}X.$

Este espacio vectorial tiene origen $c$ y formalmente debe distinguirse del espacio afín $X$ , pero la práctica habitual es denotarlo con el mismo símbolo y mencionar que es un espacio vectorial después de que se haya especificado un origen. Esta identificación permite que los puntos se consideren vectores y viceversa.

Para cualquier transformación lineal $λ$ de $V$ , podemos definir la función $L (c, λ) : X \to X$ por

L(c,\lambda )(x)=m_{c}^{-1}\left(\lambda (m_{c}(x))\right)=c+\lambda ({\vec {cx}}).

Entonces $L (c, λ)$ es una transformación afín de $X$ que deja el punto $c$ fijo. ^[7] Es una transformación lineal de $X$ , vista como un espacio vectorial con origen $c$ .

Sea $σ$ cualquier transformación afín de $X.$ Elija un punto $c$ en $X$ y considere la traslación de $X$ por el vector , denotado por $T$ $w$ . Las traslaciones son transformaciones afines y la composición de las transformaciones afines es una transformación afín. Para esta elección de $c$ , existe una única transformación lineal $λ$ de $V$ tal que ^[8] ${\mathbf {w}}={\overrightarrow {c\sigma (c)}}$

\sigma(x)=T_{\mathbf {w}}\left(L(c,\lambda )(x)\right).

Es decir, una transformación afín arbitraria de $X$ es la composición de una transformación lineal de $X$ ( vista como un espacio vectorial) y una traslación de $X.$

Esta representación de transformaciones afines se toma a menudo como la definición de una transformación afín (con la elección del origen implícita). ^[9]^[10]^[11]

Representación

Como se muestra arriba, una función afín es la composición de dos funciones: una traslación y una función lineal. El álgebra vectorial ordinaria utiliza la multiplicación de matrices para representar funciones lineales y la suma de vectores para representar traslaciones. Formalmente, en el caso de dimensión finita, si la función lineal se representa como una multiplicación por una matriz invertible y la traslación como la suma de un vector , una función afín que actúa sobre un vector se puede representar como ${\estilo de visualización A}$ $\mathbf {b}$ ${\estilo de visualización f}$ $\mathbf {x}$

\mathbf {y} =f(\mathbf {x} )=A\mathbf {x} +\mathbf {b} .

Matriz aumentada

Las transformaciones afines en el plano 2D se pueden realizar mediante transformaciones lineales en tres dimensiones. La traslación se realiza mediante cizallamiento a lo largo del eje z y la rotación se realiza alrededor del eje z.

Utilizando una matriz aumentada y un vector aumentado, es posible representar tanto la traslación como la función lineal utilizando una única multiplicación de matrices . La técnica requiere que todos los vectores se aumenten con un "1" al final, y todas las matrices se aumenten con una fila adicional de ceros en la parte inferior, una columna adicional (el vector de traslación) a la derecha y un "1" en la esquina inferior derecha. Si es una matriz, ${\estilo de visualización A}$

{\begin{bmatrix}\mathbf {y} \\1\end{bmatrix}}=\left[{\begin{array}{ccc|c}&A&&\mathbf {b} \\0&\cdots &0&1\end{array}}\right]{\begin{bmatrix}\mathbf {x} \\1\end{bmatrix}}

es equivalente a lo siguiente

\mathbf {y} =A\mathbf {x} +\mathbf {b} .

La matriz aumentada mencionada anteriormente se denomina matriz de transformación afín . En el caso general, cuando el último vector de fila no está restringido a , la matriz se convierte en una matriz de transformación proyectiva (ya que también se puede utilizar para realizar transformaciones proyectivas ). $\left[{\begin{array}{ccc|c}0&\cdots &0&1\end{array}}\right]$

Esta representación muestra el conjunto de todas las transformaciones afines invertibles como el producto semidirecto de y . Este es un grupo bajo la operación de composición de funciones, llamado grupo afín . $Estilo de visualización K^{n}}$ $\nombre del operador {GL} (n,K)$

La multiplicación ordinaria de matrices y vectores siempre asigna el origen al origen y, por lo tanto, nunca podría representar una traslación, en la que el origen debe asignarse necesariamente a algún otro punto. Al agregar la coordenada adicional "1" a cada vector, se considera esencialmente que el espacio que se va a asignar es un subconjunto de un espacio con una dimensión adicional. En ese espacio, el espacio original ocupa el subconjunto en el que la coordenada adicional es 1. Por lo tanto, el origen del espacio original se puede encontrar en . Entonces es posible una traslación dentro del espacio original por medio de una transformación lineal del espacio de dimensión superior (específicamente, una transformación de cizallamiento). Las coordenadas en el espacio de dimensión superior son un ejemplo de coordenadas homogéneas . Si el espacio original es euclidiano , el espacio de dimensión superior es un espacio proyectivo real . $(0,0,\puntos,0,1)$

La ventaja de utilizar coordenadas homogéneas es que se pueden combinar cualquier número de transformaciones afines en una sola multiplicando las matrices respectivas. Esta propiedad se utiliza ampliamente en gráficos por computadora , visión artificial y robótica .

Ejemplo de matriz aumentada

Supóngase que tiene tres puntos que definen un triángulo no degenerado en un plano, o cuatro puntos que definen un tetraedro no degenerado en un espacio tridimensional, o en general $n + 1$ puntos $x 1$ , ..., $x n + 1$ que definen un símplex no degenerado en un espacio $n$ -dimensional. Supóngase que tiene puntos de destino correspondientes $y 1$ , ..., $y n + 1$ , donde estos nuevos puntos pueden estar en un espacio con cualquier número de dimensiones. (Además, los nuevos puntos no necesitan ser distintos entre sí y no necesitan formar un símplex no degenerado). La única matriz aumentada $M$ que logra la transformación afín es ${\begin{bmatrix}\mathbf {y} \\1\end{bmatrix}}=M{\begin{bmatrix}\mathbf {x} \\1\end{bmatrix}}$ $M={\begin{bmatrix}\mathbf {y} _{1}&\cdots &\mathbf {y} _{n+1}\\1&\cdots &1\end{bmatrix}}{\begin{bmatrix}\mathbf {x} _{1}&\cdots &\mathbf {x} _{n+1}\\1&\cdots &1\end{bmatrix}}^{-1}.$

Propiedades

Propiedades preservadas

Una transformación afín conserva:

colinealidad entre puntos: tres o más puntos que se encuentran en la misma línea (llamados puntos colineales) continúan siendo colineales después de la transformación.
paralelismo : dos o más líneas que son paralelas, continúan siendo paralelas después de la transformación.
Convexidad de los conjuntos: un conjunto convexo continúa siendo convexo después de la transformación. Además, los puntos extremos del conjunto original se asignan a los puntos extremos del conjunto transformado. ^[12]
razones de longitudes de segmentos de líneas paralelas: para segmentos paralelos distintos definidos por los puntos y , y , la razón de y es la misma que la de y . $estilo de visualización p_{1}}$ $estilo de visualización p_{2}$ $estilo de visualización p_{3}$ $estilo de visualización p_{4}}$ ${\overrightarrow {p_{1}p_{2}}}$ ${\overrightarrow {p_{3}p_{4}}}$ ${\overrightarrow {f(p_{1})f(p_{2})}}$ ${\overrightarrow {f(p_{3})f(p_{4})}}$
baricentros de colecciones ponderadas de puntos.

Grupos

Como una transformación afín es invertible , la matriz cuadrada que aparece en su representación matricial es invertible . La representación matricial de la transformación inversa es entonces ${\estilo de visualización A}$

\left[{\begin{array}{ccc|c}&A^{-1}&&-A^{-1}{\vec {b}}\ \\0&\ldots &0&1\end{array}}\right].

Las transformaciones afines invertibles (de un espacio afín sobre sí mismo) forman el grupo afín , que tiene como subgrupo al grupo lineal general de grado y es a su vez un subgrupo del grupo lineal general de grado . ${\estilo de visualización n}$ $n+1$

Las transformaciones de similitud forman el subgrupo donde es un escalar multiplicado por una matriz ortogonal . Por ejemplo, si la transformación afín actúa sobre el plano y si el determinante de es 1 o −1, entonces la transformación es una aplicación equiárea . Tales transformaciones forman un subgrupo llamado grupo equiafín . ^[13] Una transformación que es a la vez equiafín y una similitud es una isometría del plano tomada con la distancia euclidiana . $A$ $A$

Cada uno de estos grupos tiene un subgrupo de transformaciones afines positivas o que preservan la orientación : aquellas en las que el determinante de es positivo. En este último caso, se trata en 3D del grupo de transformaciones rígidas ( rotaciones propias y traslaciones puras). $A$

Si hay un punto fijo, podemos tomarlo como el origen y la transformación afín se reduce a una transformación lineal. Esto puede facilitar la clasificación y la comprensión de la transformación. Por ejemplo, describir una transformación como una rotación en un cierto ángulo con respecto a un cierto eje puede dar una idea más clara del comportamiento general de la transformación que describirla como una combinación de una traslación y una rotación. Sin embargo, esto depende de la aplicación y el contexto.

Mapas afines

Una función afín entre dos espacios afines es una función sobre los puntos que actúa linealmente sobre los vectores (es decir, los vectores entre puntos del espacio). En símbolos, determina una transformación lineal tal que, para cualquier par de puntos : $f\colon {\mathcal {A}}\to {\mathcal {B}}$ $f$ $\varphi$ $P,Q\in {\mathcal {A}}$

{\overrightarrow {f(P)~f(Q)}}=\varphi ({\overrightarrow {PQ}})

f(Q)-f(P)=\varphi (Q-P)

Podemos interpretar esta definición de otras maneras, como sigue:

Si se elige un origen y se denota su imagen , entonces esto significa que para cualquier vector : $O\in {\mathcal {A}}$ $B$ $f(O)\in {\mathcal {B}}$ ${\vec {x}}$

f\colon (O+{\vec {x}})\mapsto (B+\varphi ({\vec {x}}))

Si también se elige un origen , este se puede descomponer como una transformación afín que envía , es decir $O'\in {\mathcal {B}}$ $g\colon {\mathcal {A}}\to {\mathcal {B}}$ $O\mapsto O'$

g\colon (O+{\vec {x}})\mapsto (O'+\varphi ({\vec {x}}))

seguido de la traducción por un vector . ${\vec {b}}={\overrightarrow {O'B}}$

La conclusión es que, intuitivamente, consiste en una traslación y un mapa lineal. $f$

Definición alternativa

Dados dos espacios afines y , sobre el mismo cuerpo, una función es una función afín si y sólo si para cada familia de puntos ponderados en tales que ${\mathcal {A}}$ ${\mathcal {B}}$ $f\colon {\mathcal {A}}\to {\mathcal {B}}$ $\{(a_{i},\lambda _{i})\}_{i\in I}$ ${\mathcal {A}}$

\sum _{i\in I}\lambda _{i}=1

tenemos ^[14]

f\left(\sum _{i\in I}\lambda _{i}a_{i}\right)=\sum _{i\in I}\lambda _{i}f(a_{i})

En otras palabras, conserva los baricentros . $f$

Historia

La palabra "afín" como término matemático se define en relación con las tangentes a las curvas en la Introductio in analysin infinitorum de Euler de 1748. ^[15] Felix Klein atribuye el término "transformación afín" a Möbius y Gauss . ^[10]

Transformación de imagen

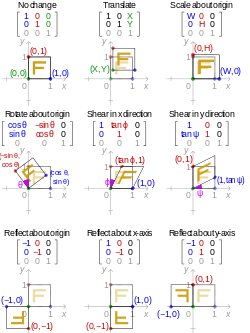
En sus aplicaciones al procesamiento de imágenes digitales , las transformaciones afines son análogas a imprimir sobre una lámina de caucho y estirar los bordes de la lámina en paralelo al plano. Esta transformación reubica los píxeles, lo que requiere una interpolación de intensidad para aproximar el valor de los píxeles movidos; la interpolación bicúbica es el estándar para las transformaciones de imágenes en aplicaciones de procesamiento de imágenes. Las transformaciones afines escalan, rotan, trasladan, reflejan y cortan imágenes como se muestra en los siguientes ejemplos: ^[16]

Las transformaciones afines son aplicables al proceso de registro en el que se alinean (registran) dos o más imágenes. Un ejemplo de registro de imágenes es la generación de imágenes panorámicas que son el producto de la unión de varias imágenes .

Deformación afín

La transformación afín conserva las líneas paralelas. Sin embargo, las transformaciones de estiramiento y de corte deforman las formas, como se muestra en el siguiente ejemplo:

Este es un ejemplo de deformación de la imagen. Sin embargo, las transformaciones afines no facilitan la proyección sobre una superficie curva ni las distorsiones radiales .

En el avión

Las transformaciones afines en dos dimensiones reales incluyen:

traducciones puras,
escala en una dirección dada, con respecto a una línea en otra dirección (no necesariamente perpendicular), combinada con una traslación que no es puramente en la dirección de escala; tomando "escalamiento" en un sentido generalizado incluye los casos en que el factor de escala es cero ( proyección ) o negativo; este último incluye la reflexión , y combinado con la traslación incluye la reflexión de deslizamiento ,
rotación combinada con una homotecia y una traslación,
Mapeo de corte combinado con una homotecia y una traslación, o
Mapeo de compresión combinado con una homotecia y una traducción.

Para visualizar la transformación afín general del plano euclidiano , tomemos los paralelogramos etiquetados ABCD y A′B′C′D′ . Cualquiera que sea la elección de puntos, existe una transformación afín T del plano que lleva A a A′ , y cada vértice de manera similar. Suponiendo que excluimos el caso degenerado donde ABCD tiene área cero , existe una única transformación afín T. Dibujando una cuadrícula completa de paralelogramos basada en ABCD , la imagen T ( P ) de cualquier punto P se determina notando que T ( A ) = A′ , T aplicada al segmento de línea AB es A′B′ , T aplicada al segmento de línea AC es A′C′ , y T respeta múltiplos escalares de vectores basados en A. [Si A , E , F son colineales entonces la relación longitud( AF )/longitud( AE ) es igual a longitud( A′F ′ )/longitud( A′E ′ ).] Geométricamente T transforma la cuadrícula basada en ABCD a aquella basada en A′B′C′D′ .

Las transformaciones afines no respetan longitudes ni ángulos; multiplican el área por un factor constante

área de A′B′C′D′ / área de ABCD .

Una T dada puede ser directa (orientación respecto de otra) o indirecta (orientación inversa), y esto puede determinarse por su efecto sobre áreas con signo (como se define, por ejemplo, por el producto vectorial de vectores).

Ejemplos

Sobre los números reales

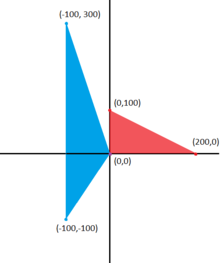
Las funciones con y en y , son precisamente las transformaciones afines de la recta real . $f\colon \mathbb {R} \to \mathbb {R} ,\;f(x)=mx+c$ $m$ $c$ $\mathbb {R}$ $m\neq 0$

En geometría plana

En , la transformación que se muestra a la izquierda se logra utilizando el mapa dado por: $\mathbb {R} ^{2}$

{\begin{bmatrix}x\\y\end{bmatrix}}\mapsto {\begin{bmatrix}0&1\\2&1\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}+{\begin{bmatrix}-100\\-100\end{bmatrix}}

Al transformar los tres vértices del triángulo original (en rojo), se obtienen tres nuevos puntos que forman el nuevo triángulo (en azul). Esta transformación distorsiona y traslada el triángulo original.

De hecho, todos los triángulos están relacionados entre sí mediante transformaciones afines. Esto también es cierto para todos los paralelogramos, pero no para todos los cuadriláteros.

Véase también

Anamorfosis : aplicaciones artísticas de transformaciones afines
Geometría afín
Proyección 3D
Homografía
Plano (geometría)
Función doblada

Notas

^ Berger 1987, pág. 38.
^ Samuel 1988, pág. 11.
^ Snapper y Troyer 1989, pág. 65.
^ Snapper y Troyer 1989, pág. 66.
^ Snapper y Troyer 1989, pág. 69.
^ Snapper y Troyer 1989, pág. 59.
^ Snapper y Troyer 1989, págs. 76,87.
^ Snapper y Troyer 1989, pág. 86.
^ Wan 1993, págs. 19-20.
^ desde Klein 1948, pág. 70.
^ Brannan, Esplen y Gray 1999, pág. 53.
^ Reinhard Schultz. "Transformaciones afines y convexidad" (PDF) . Consultado el 27 de febrero de 2017 .
^ Oswald Veblen (1918) Geometría proyectiva , volumen 2, págs. 105–7.
^ Schneider, Philip K.; Eberly, David H. (2003). Herramientas geométricas para gráficos por computadora. Morgan Kaufmann. pág. 98. ISBN 978-1-55860-594-7.
^ Euler, Leonhard (1748). Introductio in analysin infinitorum (en latín). vol. II.Libro II, secc. XVIII, art. 442
^ González, Rafael (2008).'Procesamiento de imágenes digitales, 3.º grado'. Salón Pearson. ISBN 9780131687288.

Referencias

Berger, Marcel (1987), Geometría I , Berlín: Springer, ISBN 3-540-11658-3
Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999), Geometría , Cambridge University Press, ISBN 978-0-521-59787-6
Nomizu, Katsumi ; Sasaki, S. (1994), Geometría diferencial afín (nueva ed.), Cambridge University Press, ISBN 978-0-521-44177-3
Klein, Felix (1948) [1939], Matemáticas elementales desde un punto de vista avanzado: geometría , Dover
Samuel, Pierre (1988), Geometría proyectiva , Springer-Verlag, ISBN 0-387-96752-4
Sharpe, RW (1997). Geometría diferencial: la generalización de Cartan del programa de Erlangen de Klein . Nueva York: Springer. ISBN 0-387-94732-9.
Snapper, Ernst; Troyer, Robert J. (1989) [1971], Geometría afín métrica , Dover, ISBN 978-0-486-66108-7
Wan, Zhe-xian (1993), Geometría de grupos clásicos sobre cuerpos finitos , Chartwell-Bratt, ISBN 0-86238-326-9

Enlaces externos

Medios relacionados con Transformación afín en Wikimedia Commons
"Transformación afín", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
Operaciones geométricas: transformada afín, R. Fisher, S. Perkins, A. Walker y E. Wolfart.
Weisstein, Eric W. "Transformación afín". MundoMatemático .
Transformada afín de Bernard Vuilleumier, Proyecto de demostraciones Wolfram .
Transformación afín con MATLAB