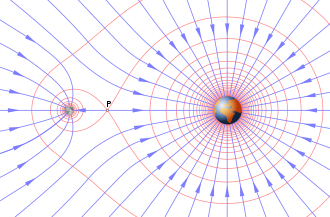
En física , un campo gravitatorio o campo de aceleración gravitatoria es un campo vectorial utilizado para explicar las influencias que un cuerpo extiende en el espacio que lo rodea. [1] Un campo gravitatorio se utiliza para explicar fenómenos gravitatorios , como el campo de fuerza gravitatoria ejercido sobre otro cuerpo masivo. Tiene dimensión de aceleración (L/T 2 ) y se mide en unidades de newtons por kilogramo (N/kg) o, equivalentemente, en metros por segundo al cuadrado (m/s 2 ).
En su concepto original, la gravedad era una fuerza entre masas puntuales . Siguiendo a Isaac Newton , Pierre-Simon Laplace intentó modelar la gravedad como una especie de campo de radiación o fluido , [ cita requerida ] y desde el siglo XIX, las explicaciones de la gravedad en la mecánica clásica se han enseñado generalmente en términos de un modelo de campo, en lugar de una atracción puntual. Resulta del gradiente espacial del campo de potencial gravitatorio .
En la relatividad general , en lugar de que dos partículas se atraigan entre sí, las partículas distorsionan el espacio-tiempo a través de su masa, y esta distorsión es lo que se percibe y mide como una "fuerza". [ cita requerida ] En un modelo de este tipo, se afirma que la materia se mueve de ciertas maneras en respuesta a la curvatura del espacio-tiempo, [2] y que no hay fuerza gravitacional , [3] o que la gravedad es una fuerza ficticia . [4]
La gravedad se distingue de otras fuerzas por su obediencia al principio de equivalencia .
En mecánica clásica, un campo gravitatorio es una cantidad física. [5] Un campo gravitatorio se puede definir utilizando la ley de gravitación universal de Newton . Determinado de esta manera, el campo gravitatorio g alrededor de una sola partícula de masa M es un campo vectorial que consiste en cada punto de un vector que apunta directamente hacia la partícula. La magnitud del campo en cada punto se calcula aplicando la ley universal, y representa la fuerza por unidad de masa sobre cualquier objeto en ese punto en el espacio. Debido a que el campo de fuerza es conservativo, hay una energía potencial escalar por unidad de masa, Φ , en cada punto en el espacio asociada con los campos de fuerza; esto se llama potencial gravitatorio . [6] La ecuación del campo gravitacional es [7] donde F es la fuerza gravitacional , m es la masa de la partícula de prueba , R es el vector radial de la partícula de prueba en relación con la masa (o para la segunda ley de movimiento de Newton, que es una función dependiente del tiempo, un conjunto de posiciones de partículas de prueba, cada una de las cuales ocupa un punto particular en el espacio para el inicio de la prueba), t es el tiempo , G es la constante gravitacional y ∇ es el operador del .
Esto incluye la ley de gravitación universal de Newton y la relación entre el potencial gravitacional y la aceleración del campo.el 2R/el t2 y F/metro son ambas iguales a la aceleración gravitacional g (equivalente a la aceleración inercial, por lo que la misma forma matemática, pero también definida como fuerza gravitacional por unidad de masa [8] ). Los signos negativos se insertan ya que la fuerza actúa antiparalelamente al desplazamiento. La ecuación de campo equivalente en términos de densidad de masa ρ de la masa que atrae es: que contiene la ley de Gauss para la gravedad y la ecuación de Poisson para la gravedad . La ley de Newton implica la ley de Gauss, pero no al revés; consulte Relación entre las leyes de Gauss y Newton .
Estas ecuaciones clásicas son ecuaciones diferenciales de movimiento para una partícula de prueba en presencia de un campo gravitacional, es decir, establecer y resolver estas ecuaciones permite determinar y describir el movimiento de una masa de prueba.
El campo alrededor de múltiples partículas es simplemente la suma vectorial de los campos alrededor de cada partícula individual. Una partícula de prueba en dicho campo experimentará una fuerza que es igual a la suma vectorial de las fuerzas que experimentaría en estos campos individuales. Esto es [9] es decir, el campo gravitacional sobre la masa m j es la suma de todos los campos gravitacionales debidos a todas las demás masas m i , excepto la masa m j misma. R i es el vector de posición de la partícula gravitante i , y R es el de la partícula de prueba.
En la relatividad general , los símbolos de Christoffel desempeñan el papel del campo de fuerza gravitacional y el tensor métrico desempeña el papel del potencial gravitacional.
En la relatividad general, el campo gravitacional se determina resolviendo las ecuaciones de campo de Einstein [10] donde T es el tensor de tensión-energía , G es el tensor de Einstein y κ es la constante gravitacional de Einstein . Esta última se define como κ = 8 πG / c 4 , donde G es la constante de gravitación newtoniana y c es la velocidad de la luz .
Estas ecuaciones dependen de la distribución de la materia, la tensión y el momento en una región del espacio, a diferencia de la gravedad newtoniana, que depende únicamente de la distribución de la materia. Los campos en sí mismos en la relatividad general representan la curvatura del espacio-tiempo. La relatividad general establece que estar en una región del espacio curvado es equivalente a acelerar hacia arriba del gradiente del campo. Según la segunda ley de Newton , esto hará que un objeto experimente una fuerza ficticia si se mantiene quieto con respecto al campo. Es por eso que una persona se sentirá atraída hacia abajo por la fuerza de la gravedad mientras se mantiene quieta en la superficie de la Tierra. En general, los campos gravitatorios predichos por la relatividad general difieren en sus efectos solo ligeramente de los predichos por la mecánica clásica, pero hay una serie de diferencias fácilmente verificables , una de las más conocidas es la desviación de la luz en dichos campos.
Los diagramas de incrustación son gráficos tridimensionales que se utilizan comúnmente para ilustrar de forma educativa el potencial gravitacional dibujando campos de potencial gravitacional como una topografía gravitacional y representando los potenciales como los llamados pozos gravitacionales o esferas de influencia .
'campo' es cualquier cantidad física que adquiere valores diferentes en diferentes puntos del espacio.