La planificación del movimiento , también llamada planificación de trayectoria (también conocida como el problema de navegación o el problema del movedor de piano ), es un problema computacional que busca encontrar una secuencia de configuraciones válidas que muevan el objeto desde el origen hasta el destino. El término se utiliza en geometría computacional , animación por computadora , robótica y juegos de computadora .
Por ejemplo, considere la posibilidad de navegar un robot móvil dentro de un edificio hasta un punto de referencia distante. Debería ejecutar esta tarea evitando las paredes y sin caerse por las escaleras. Un algoritmo de planificación de movimiento tomaría una descripción de estas tareas como entrada y generaría los comandos de velocidad y giro enviados a las ruedas del robot. Los algoritmos de planificación de movimiento podrían abordar robots con una mayor cantidad de articulaciones (por ejemplo, manipuladores industriales), tareas más complejas (por ejemplo, manipulación de objetos), diferentes restricciones (por ejemplo, un automóvil que solo puede avanzar) e incertidumbre (por ejemplo, modelos imperfectos del entorno o del robot).
La planificación del movimiento tiene varias aplicaciones en robótica, como la autonomía , la automatización y el diseño de robots en software CAD , así como aplicaciones en otros campos, como la animación de personajes digitales , los videojuegos , el diseño arquitectónico , la cirugía robótica y el estudio de moléculas biológicas .

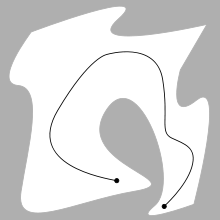

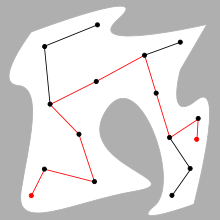
Un problema básico de planificación de movimiento es calcular una ruta continua que conecte una configuración de inicio S y una configuración de destino G, evitando al mismo tiempo la colisión con obstáculos conocidos. La geometría del robot y del obstáculo se describe en un espacio de trabajo 2D o 3D, mientras que el movimiento se representa como una ruta en un espacio de configuración (posiblemente de mayor dimensión) .
Una configuración describe la postura del robot y el espacio de configuración C es el conjunto de todas las configuraciones posibles. Por ejemplo:
El conjunto de configuraciones que evita la colisión con obstáculos se denomina espacio libre C libre . El complemento de C libre en C se denomina obstáculo o región prohibida.
A menudo, resulta prohibitivamente difícil calcular explícitamente la forma de C free . Sin embargo, probar si una configuración dada está en C free es eficiente. Primero, la cinemática directa determina la posición de la geometría del robot y la detección de colisiones prueba si la geometría del robot colisiona con la geometría del entorno.
El espacio objetivo es un subespacio del espacio libre que indica hacia dónde queremos que se mueva el robot. En la planificación de movimiento global, el espacio objetivo es observable por los sensores del robot. Sin embargo, en la planificación de movimiento local, el robot no puede observar el espacio objetivo en algunos estados. Para resolver este problema, el robot pasa por varios espacios objetivo virtuales, cada uno de los cuales se encuentra dentro del área observable (alrededor del robot). Un espacio objetivo virtual se denomina subobjetivo.
El espacio de obstáculos es un espacio al que el robot no puede desplazarse. El espacio de obstáculos no es lo opuesto al espacio libre.
Los problemas de baja dimensión se pueden resolver con algoritmos basados en cuadrículas que superponen una cuadrícula sobre el espacio de configuración, o algoritmos geométricos que calculan la forma y la conectividad de C libre .
La planificación exacta del movimiento para sistemas de alta dimensión bajo restricciones complejas es computacionalmente intratable . Los algoritmos de campo potencial son eficientes, pero caen presa de los mínimos locales (una excepción son los campos de potencial armónicos). Los algoritmos basados en muestreo evitan el problema de los mínimos locales y resuelven muchos problemas con bastante rapidez. No pueden determinar que no existe una ruta, pero tienen una probabilidad de falla que disminuye a cero a medida que se pasa más tiempo. [ cita requerida ]
Los algoritmos basados en muestreo se consideran actualmente [ ¿cuándo? ] el estado del arte para la planificación del movimiento en espacios de alta dimensión, y se han aplicado a problemas que tienen docenas o incluso cientos de dimensiones (manipuladores robóticos, moléculas biológicas, personajes digitales animados y robots con patas ).
Los enfoques basados en cuadrículas superponen una cuadrícula en el espacio de configuración y suponen que cada configuración se identifica con un punto de cuadrícula. En cada punto de cuadrícula, el robot puede moverse a puntos de cuadrícula adyacentes siempre que la línea entre ellos esté completamente contenida dentro de C libre (esto se prueba con detección de colisiones). Esto discretiza el conjunto de acciones y se utilizan algoritmos de búsqueda (como A* ) para encontrar una ruta desde el inicio hasta el objetivo.
Estos enfoques requieren establecer una resolución de cuadrícula. La búsqueda es más rápida con cuadrículas más gruesas, pero el algoritmo no podrá encontrar rutas a través de porciones estrechas de C libre . Además, la cantidad de puntos en la cuadrícula crece exponencialmente en la dimensión del espacio de configuración, lo que los hace inadecuados para problemas de alta dimensión.
Los enfoques tradicionales basados en cuadrículas producen rutas cuyos cambios de rumbo están restringidos a múltiplos de un ángulo base determinado, lo que a menudo da como resultado rutas subóptimas. Los enfoques de planificación de rutas con cualquier ángulo encuentran rutas más cortas propagando información a lo largo de los bordes de la cuadrícula (para buscar rápidamente) sin restringir sus rutas a los bordes de la cuadrícula (para encontrar rutas cortas).
Los enfoques basados en cuadrículas suelen necesitar realizar búsquedas repetidas, por ejemplo, cuando cambia el conocimiento del robot sobre el espacio de configuración o cuando el espacio de configuración en sí cambia durante el seguimiento de la ruta. Los algoritmos de búsqueda heurística incremental replanifican rápidamente utilizando la experiencia con problemas de planificación de rutas similares anteriores para acelerar la búsqueda del problema actual.
Estos enfoques son similares a los enfoques de búsqueda basados en cuadrículas, excepto que generan un pavimento que cubre completamente el espacio de configuración en lugar de una cuadrícula. [1] El pavimento se descompone en dos subpavimentos X − ,X + hechos con cajas tales que X − ⊂ C libre ⊂ X + . Caracterizar C libre equivale a resolver un problema de inversión de conjuntos . Por lo tanto, el análisis de intervalos podría usarse cuando C libre no puede describirse mediante desigualdades lineales para tener un cerramiento garantizado.
De esta manera, el robot puede moverse libremente en X − y no puede salir de X + . Para ambos subpavimentos, se construye un grafo vecino y se pueden encontrar caminos utilizando algoritmos como Dijkstra o A* . Cuando un camino es factible en X − , también es factible en C free . Cuando no existe un camino en X + desde una configuración inicial hasta el objetivo, tenemos la garantía de que no existe un camino factible en C free . En cuanto al enfoque basado en cuadrícula, el enfoque de intervalo es inadecuado para problemas de alta dimensión, debido al hecho de que el número de cajas a generar crece exponencialmente con respecto a la dimensión del espacio de configuración.
Una ilustración de ello la proporcionan las tres figuras de la derecha, en las que un gancho con dos grados de libertad tiene que moverse de izquierda a derecha evitando dos pequeños segmentos horizontales.



Nicolas Delanoue ha demostrado que la descomposición con subpavimentos mediante análisis de intervalos también permite caracterizar la topología de C libre , por ejemplo contando su número de componentes conectados. [2]
Apunta robots entre obstáculos poligonales
Trasladar objetos entre obstáculos
Encontrar la salida de un edificio
Dado un haz de rayos alrededor de la posición actual cuya longitud impacta contra una pared, el robot se mueve en la dirección del rayo más largo a menos que identifique una puerta. Este algoritmo se utilizó para modelar la salida de emergencia de los edificios.
Un enfoque consiste en tratar la configuración del robot como un punto en un campo potencial que combina la atracción hacia el objetivo y la repulsión hacia los obstáculos. La trayectoria resultante se obtiene como el camino. Este enfoque tiene ventajas en el sentido de que la trayectoria se produce con poco cálculo. Sin embargo, pueden quedar atrapados en mínimos locales del campo potencial y no encontrar un camino, o pueden encontrar un camino no óptimo. Los campos potenciales artificiales se pueden tratar como ecuaciones continuas similares a los campos potenciales electrostáticos (tratando al robot como una carga puntual), o el movimiento a través del campo se puede discretizar utilizando un conjunto de reglas lingüísticas. [3] Una función de navegación [4] o una función de navegación probabilística [5] son tipos de funciones potenciales artificiales que tienen la cualidad de no tener puntos mínimos excepto el punto objetivo.
Los algoritmos basados en muestreo representan el espacio de configuración con una hoja de ruta de configuraciones muestreadas. Un algoritmo básico muestrea N configuraciones en C y conserva aquellas en C libres para usarlas como hitos . Luego se construye una hoja de ruta que conecta dos hitos P y Q si el segmento de línea PQ está completamente en C libre . Nuevamente, se utiliza la detección de colisiones para probar la inclusión en C libre . Para encontrar una ruta que conecte S y G, se agregan a la hoja de ruta. Si una ruta en la hoja de ruta vincula S y G, el planificador tiene éxito y devuelve esa ruta. Si no, la razón no es definitiva: o no hay una ruta en C libre o el planificador no muestreó suficientes hitos.
Estos algoritmos funcionan bien para espacios de configuración de alta dimensión, porque a diferencia de los algoritmos combinatorios, su tiempo de ejecución no depende (explícitamente) de manera exponencial de la dimensión de C. También son (en general) sustancialmente más fáciles de implementar. Son probabilísticamente completos, lo que significa que la probabilidad de que produzcan una solución se acerca a 1 a medida que se dedica más tiempo. Sin embargo, no pueden determinar si no existe una solución.
Dadas las condiciones básicas de visibilidad en C free , se ha demostrado que a medida que aumenta el número de configuraciones N, la probabilidad de que el algoritmo anterior encuentre una solución se acerca a 1 exponencialmente. [6] La visibilidad no depende explícitamente de la dimensión de C; es posible tener un espacio de alta dimensión con una visibilidad "buena" o un espacio de baja dimensión con una visibilidad "mala". El éxito experimental de los métodos basados en muestras sugiere que los espacios más comúnmente vistos tienen una buena visibilidad.
Existen muchas variantes de este esquema básico:
Se dice que un planificador de movimiento está completo si produce una solución en un tiempo finito o bien informa correctamente que no existe ninguna. La mayoría de los algoritmos completos se basan en la geometría. El rendimiento de un planificador completo se evalúa por su complejidad computacional . Al demostrar esta propiedad matemáticamente, hay que asegurarse de que ocurra en un tiempo finito y no sólo en el límite asintótico. Esto es especialmente problemático si se producen secuencias infinitas (que convergen sólo en el caso límite) durante una técnica de demostración específica, ya que entonces, teóricamente, el algoritmo nunca se detendrá. Normalmente se piensa erróneamente que los "trucos" intuitivos (a menudo basados en la inducción) convergen, lo que ocurre sólo para el límite infinito. En otras palabras, la solución existe, pero el planificador nunca la informará. Por tanto, esta propiedad está relacionada con la completitud de Turing y sirve en la mayoría de los casos como fundamento/guía teórica. Los planificadores basados en un enfoque de fuerza bruta siempre están completos, pero sólo son realizables para configuraciones finitas y discretas.
En la práctica, la terminación del algoritmo siempre se puede garantizar utilizando un contador, que permite sólo un número máximo de iteraciones y luego siempre se detiene con o sin solución. Para sistemas en tiempo real, esto se logra típicamente utilizando un temporizador de vigilancia , que simplemente matará el proceso. El perro guardián tiene que ser independiente de todos los procesos (normalmente realizado por rutinas de interrupción de bajo nivel). El caso asintótico descrito en el párrafo anterior, sin embargo, no se alcanzará de esta manera. Informará el mejor que ha encontrado hasta ahora (que es mejor que nada) o ninguno, pero no puede informar correctamente que no hay ninguno. Todas las realizaciones que incluyen un perro guardián siempre son incompletas (excepto que todos los casos se pueden evaluar en tiempo finito).
La completitud solo se puede garantizar mediante una prueba matemática de corrección muy rigurosa (a menudo asistida por herramientas y métodos basados en gráficos) y solo debe ser realizada por expertos especializados si la aplicación incluye contenido de seguridad. Por otro lado, refutar la completitud es fácil, ya que solo se necesita encontrar un bucle infinito o un resultado incorrecto devuelto. La verificación formal/corrección de algoritmos es un campo de investigación en sí mismo. La configuración correcta de estos casos de prueba es una tarea altamente sofisticada.
La completitud de la resolución es la propiedad que garantiza que el planificador encuentre una ruta si la resolución de una cuadrícula subyacente es lo suficientemente buena. La mayoría de los planificadores de resolución completa se basan en cuadrículas o intervalos. La complejidad computacional de los planificadores de resolución completa depende de la cantidad de puntos en la cuadrícula subyacente, que es O(1/h d ), donde h es la resolución (la longitud de un lado de una celda de la cuadrícula) y d es la dimensión del espacio de configuración.
La completitud probabilística es la propiedad según la cual, a medida que se realiza más "trabajo", la probabilidad de que el planificador no encuentre una ruta, si existe, se acerca asintóticamente a cero. Varios métodos basados en muestras son probabilísticamente completos. El rendimiento de un planificador probabilísticamente completo se mide por la tasa de convergencia. Para aplicaciones prácticas, se suele utilizar esta propiedad, ya que permite configurar el tiempo de espera del watchdog en función de un tiempo de convergencia promedio.
Los planificadores incompletos no siempre producen un camino factible cuando existe uno (véase el primer párrafo). A veces, los planificadores incompletos funcionan bien en la práctica, ya que siempre se detienen después de un tiempo garantizado y permiten que otras rutinas tomen el relevo.
Se han desarrollado muchos algoritmos para manejar variantes de este problema básico.
Los sistemas híbridos son aquellos que combinan comportamiento discreto y continuo. Algunos ejemplos de estos sistemas son:
{{cite book}}: |journal=ignorado ( ayuda )