Dislocación

Defecto o irregularidad cristalográfica lineal

Dislocaciones de tipo borde (izquierda) y tornillo (derecha).

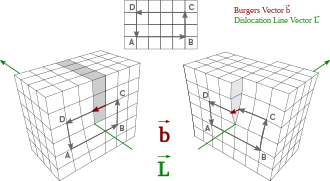
En la ciencia de los materiales , una dislocación o dislocación de Taylor es un defecto o irregularidad cristalográfica lineal dentro de una estructura cristalina que contiene un cambio abrupto en la disposición de los átomos. El movimiento de las dislocaciones permite que los átomos se deslicen unos sobre otros a niveles bajos de estrés y se conoce como deslizamiento o deslizamiento . El orden cristalino se restaura en ambos lados de una dislocación de deslizamiento , pero los átomos de un lado se han movido una posición. El orden cristalino no se restaura completamente con una dislocación parcial . Una dislocación define el límite entre las regiones deslizadas y no deslizadas del material y, como resultado, debe formar un bucle completo, intersecar otras dislocaciones o defectos, o extenderse hasta los bordes del cristal. ^{[1] [2]} Una dislocación se puede caracterizar por la distancia y la dirección del movimiento que causa a los átomos, que se define por el vector de Burgers . La deformación plástica de un material ocurre por la creación y el movimiento de muchas dislocaciones. El número y la disposición de las dislocaciones influyen en muchas de las propiedades de los materiales .

Los dos tipos principales de dislocaciones son las dislocaciones sésiles , que son inmóviles, y las dislocaciones deslizantes, que son móviles. ^[3] Algunos ejemplos de dislocaciones sésiles son la dislocación en escalera y la unión de Lomer-Cottrell . Los dos tipos principales de dislocaciones móviles son las dislocaciones de borde y las dislocaciones en tornillo .

Las dislocaciones de borde se pueden visualizar como causadas por la terminación de un plano de átomos en el medio de un cristal . En tal caso, los planos circundantes no son rectos, sino que se curvan alrededor del borde del plano de terminación de modo que la estructura cristalina está perfectamente ordenada en ambos lados. Este fenómeno es análogo a la mitad de una hoja de papel insertada en una pila de papeles, donde el defecto en la pila es perceptible solo en el borde de la mitad de la hoja.

La teoría que describe los campos elásticos de los defectos fue desarrollada originalmente por Vito Volterra en 1907. En 1934, Egon Orowan , Michael Polanyi y GI Taylor , propusieron que las bajas tensiones observadas que producen deformación plástica en comparación con las predicciones teóricas de la época podrían explicarse en términos de la teoría de dislocaciones.

Historia

La teoría que describe los campos elásticos de los defectos fue desarrollada originalmente por Vito Volterra en 1907. ^[4] El término "dislocación" que se refiere a un defecto a escala atómica fue acuñado por GI Taylor en 1934. ^[5]

Antes de la década de 1930, uno de los desafíos más persistentes de la ciencia de los materiales era explicar la plasticidad en términos microscópicos. Un intento simplista de calcular la tensión de corte a la que los planos atómicos vecinos se deslizan uno sobre el otro en un cristal perfecto sugiere que, para un material con módulo de corte , la resistencia al corte viene dada aproximadamente por: ${\displaystyle G}$ ${\displaystyle \tau _{m}}$

${\displaystyle \tau _{m}={\frac {G}{2\pi }}.}$

El módulo de corte de los metales se encuentra normalmente en el rango de 20 000 a 150 000 MPa, lo que indica una tensión de corte prevista de 3 000 a 24 000 MPa. Esto era difícil de conciliar con tensiones de corte medidas en el rango de 0,5 a 10 MPa.

En 1934, Egon Orowan , Michael Polanyi y GI Taylor propusieron de forma independiente que la deformación plástica podía explicarse en términos de la teoría de las dislocaciones. Las dislocaciones pueden moverse si los átomos de uno de los planos circundantes rompen sus enlaces y se vuelven a unir con los átomos del borde terminal. En efecto, un semiplano de átomos se mueve en respuesta a la tensión de corte rompiendo y reformando una línea de enlaces, uno (o unos pocos) a la vez. La energía necesaria para romper una fila de enlaces es mucho menor que la necesaria para romper todos los enlaces de un plano entero de átomos a la vez. Incluso este modelo simple de la fuerza necesaria para mover una dislocación muestra que la plasticidad es posible con tensiones mucho menores que en un cristal perfecto. En muchos materiales, particularmente los materiales dúctiles, las dislocaciones son las "portadoras" de la deformación plástica, y la energía necesaria para moverlas es menor que la energía necesaria para fracturar el material.

Mecanismos

Una dislocación es un defecto o irregularidad cristalográfica lineal dentro de una estructura cristalina que contiene un cambio abrupto en la disposición de los átomos. El orden cristalino se restablece en ambos lados de una dislocación, pero los átomos de un lado se han movido o deslizado. Las dislocaciones definen el límite entre las regiones deslizadas y no deslizadas del material y no pueden terminar dentro de una red y deben extenderse hasta un borde libre o formar un bucle dentro del cristal. ^[1] Una dislocación se puede caracterizar por la distancia y la dirección del movimiento que provoca en los átomos en la red, lo que se denomina vector de Burgers. El vector de Burgers de una dislocación permanece constante aunque la forma de la dislocación pueda cambiar. ^{[ cita requerida ]}

Existen diversos tipos de dislocaciones, las móviles se conocen como deslizantes y las inmóviles, como sésiles . El movimiento de las dislocaciones móviles permite que los átomos se deslicen unos sobre otros a niveles bajos de tensión y se conoce como deslizamiento. El movimiento de las dislocaciones puede verse mejorado o dificultado por la presencia de otros elementos dentro del cristal y, con el tiempo, estos elementos pueden difundirse hacia la dislocación formando una atmósfera de Cottrell . La fijación y la separación de estos elementos explican parte del comportamiento de fluencia inusual observado en los aceros. La interacción del hidrógeno con las dislocaciones es uno de los mecanismos propuestos para explicar la fragilización por hidrógeno . ^{[ cita requerida ]}

Las dislocaciones se comportan como si fueran una entidad distinta dentro de un material cristalino, donde algunos tipos de dislocaciones pueden moverse a través del material doblándose, flexionándose y cambiando de forma e interactuando con otras dislocaciones y características dentro del cristal. Las dislocaciones se generan al deformar un material cristalino como los metales, lo que puede hacer que se inicien desde las superficies, particularmente en concentraciones de tensión o dentro del material en defectos y límites de grano . La cantidad y la disposición de las dislocaciones dan lugar a muchas de las propiedades de los metales, como la ductilidad , la dureza y el límite elástico . El tratamiento térmico , el contenido de aleación y el trabajo en frío pueden cambiar la cantidad y la disposición de la población de dislocaciones y cómo se mueven e interactúan para crear propiedades útiles. ^{[ cita requerida ]}

Simulación de dislocaciones en aluminio. Se muestran únicamente átomos no cristalinos.

Generando dislocaciones

Cuando los metales se someten a un trabajo en frío (deformación a temperaturas relativamente bajas en comparación con la temperatura absoluta de fusión del material, es decir, normalmente inferiores a ), la densidad de dislocaciones aumenta debido a la formación de nuevas dislocaciones. La consiguiente superposición creciente entre los campos de deformación de las dislocaciones adyacentes aumenta gradualmente la resistencia a un mayor movimiento de las dislocaciones. Esto provoca un endurecimiento del metal a medida que avanza la deformación. Este efecto se conoce como endurecimiento por deformación o endurecimiento por trabajo. ${\displaystyle T_{m}}$ ${\displaystyle 0.4T_{m}}$

La densidad de dislocación en un material se puede incrementar mediante deformación plástica mediante la siguiente relación: ${\displaystyle \rho }$

${\displaystyle \tau \propto {\sqrt {\rho }}}$.

Dado que la densidad de dislocaciones aumenta con la deformación plástica, se debe activar un mecanismo para la creación de dislocaciones en el material. Tres mecanismos para la formación de dislocaciones son la nucleación homogénea, la iniciación de los límites de grano y las interfaces entre la red y la superficie, los precipitados, las fases dispersas o las fibras de refuerzo.

Nucleación homogénea

La creación de una dislocación por nucleación homogénea es el resultado de la ruptura de los enlaces atómicos a lo largo de una línea en la red. Un plano en la red se corta, lo que da como resultado 2 semiplanos o dislocaciones enfrentadas. Estas dislocaciones se alejan una de la otra a través de la red. Dado que la nucleación homogénea forma dislocaciones a partir de cristales perfectos y requiere la ruptura simultánea de muchos enlaces, la energía requerida para la nucleación homogénea es alta. Por ejemplo, se ha demostrado que la tensión requerida para la nucleación homogénea en el cobre es , donde es el módulo de corte del cobre (46 GPa). Resolviendo para , vemos que la tensión requerida es 3,4 GPa, que es muy cercana a la resistencia teórica del cristal. Por lo tanto, en la deformación convencional, la nucleación homogénea requiere una tensión concentrada y es muy poco probable. La iniciación del límite de grano y la interacción de la interfaz son fuentes más comunes de dislocaciones. ${\displaystyle {\frac {\tau _{\text{hom}}}{G}}=7.4\times 10^{-2}}$ ${\displaystyle G}$ ${\displaystyle \tau _{\text{hom}}\,\!}$

Las irregularidades en los límites de grano de los materiales pueden producir dislocaciones que se propagan a través del grano. Los escalones y salientes en el límite de grano son una fuente importante de dislocaciones en las primeras etapas de la deformación plástica.

Frank–Leer fuente

La fuente Frank-Read es un mecanismo capaz de producir una corriente de dislocaciones a partir de un segmento fijado de una dislocación. La tensión arquea el segmento de dislocación, expandiéndolo hasta que crea un bucle de dislocación que se libera de la fuente.

Superficies

La superficie de un cristal puede producir dislocaciones en el cristal. Debido a los pequeños escalones en la superficie de la mayoría de los cristales, la tensión en algunas regiones de la superficie es mucho mayor que la tensión media en la red. Esta tensión conduce a dislocaciones. Las dislocaciones se propagan entonces a la red de la misma manera que en la iniciación del límite de grano. En los monocristales, la mayoría de las dislocaciones se forman en la superficie. Se ha demostrado que la densidad de dislocaciones a 200 micrómetros en la superficie de un material es seis veces mayor que la densidad en masa. Sin embargo, en los materiales policristalinos las fuentes de la superficie no tienen un efecto importante porque la mayoría de los granos no están en contacto con la superficie.

Interfaces

La interfaz entre un metal y un óxido puede aumentar considerablemente la cantidad de dislocaciones creadas. La capa de óxido pone la superficie del metal en tensión porque los átomos de oxígeno se aprietan en la red y los átomos de oxígeno están bajo compresión. Esto aumenta considerablemente la tensión en la superficie del metal y, en consecuencia, la cantidad de dislocaciones formadas en la superficie. La mayor cantidad de tensión en los escalones de la superficie da como resultado un aumento en las dislocaciones formadas y emitidas desde la interfaz. ^[6]

Las dislocaciones también pueden formarse y permanecer en el plano de interfaz entre dos cristales. Esto ocurre cuando el espaciado reticular de los dos cristales no coincide, lo que da como resultado un desajuste de las redes en la interfaz. La tensión causada por el desajuste reticular se libera mediante la formación de dislocaciones desajuste espaciadas regularmente. Las dislocaciones desajuste son dislocaciones de borde con la línea de dislocación en el plano de interfaz y el vector de Burgers en la dirección de la normal de la interfaz. Las interfaces con dislocaciones desajuste pueden formarse, por ejemplo, como resultado del crecimiento epitaxial de cristales sobre un sustrato. ^[7]

Irradiación

Los bucles de dislocación pueden formarse en el daño creado por la irradiación energética . ^{[8] [9]} Un bucle de dislocación prismático puede entenderse como un disco colapsado adicional (o faltante) de átomos, y puede formarse cuando los átomos intersticiales o las vacantes se agrupan. Esto puede suceder directamente como resultado de cascadas de colisiones simples o múltiples , ^[10] lo que da como resultado densidades localmente altas de átomos intersticiales y vacantes. En la mayoría de los metales, los bucles de dislocación prismáticos son los grupos energéticamente más preferidos de átomos autointersticiales.

Interacción y disposición

Dislocaciones geométricamente necesarias

Las dislocaciones geométricamente necesarias son disposiciones de dislocaciones que pueden adaptarse a un grado limitado de flexión plástica en un material cristalino. Las marañas de dislocaciones se encuentran en la etapa temprana de deformación y aparecen como límites no bien definidos; el proceso de recuperación dinámica conduce finalmente a la formación de una estructura celular que contiene límites con una desorientación inferior a 15° (límites de grano de ángulo bajo).

Fijación

La adición de puntos de fijación que inhiben el movimiento de dislocaciones, como elementos de aleación, puede introducir campos de tensión que en última instancia fortalecen el material al requerir una mayor tensión aplicada para superar la tensión de fijación y continuar el movimiento de dislocación.

Los efectos del endurecimiento por deformación por acumulación de dislocaciones y la estructura de grano formada a alta deformación se pueden eliminar mediante un tratamiento térmico adecuado ( recocido ) que promueve la recuperación y posterior recristalización del material.

Las técnicas de procesamiento combinadas de endurecimiento por trabajo y recocido permiten controlar la densidad de dislocaciones, el grado de enredo de dislocaciones y, en última instancia, la resistencia al rendimiento del material.

Bandas de deslizamiento persistentes

El ciclo repetido de un material puede generar y agrupar dislocaciones rodeadas de regiones que están relativamente libres de dislocaciones. Este patrón forma una estructura en forma de escalera conocida como bandas de deslizamiento persistentes (PSB). ^[11] Las PSB se denominan así porque dejan marcas en la superficie de los metales que, incluso cuando se eliminan mediante pulido, vuelven al mismo lugar con el ciclo continuo.

Las paredes de PSB están formadas predominantemente por dislocaciones de borde. Entre las paredes, la plasticidad se transmite mediante dislocaciones de tornillo. ^[11]

Donde los PSB se encuentran con la superficie, se forman extrusiones e intrusiones que, bajo cargas cíclicas repetidas, pueden provocar el inicio de una grieta por fatiga . ^[12]

Movimiento

Planeo

Las dislocaciones pueden deslizarse en planos que contienen tanto la línea de dislocación como el vector de Burgers, el llamado plano de deslizamiento. ^[13] Para una dislocación helicoidal, la línea de dislocación y el vector de Burgers son paralelos, por lo que la dislocación puede deslizarse en cualquier plano que contenga la dislocación. Para una dislocación de borde, la dislocación y el vector de Burgers son perpendiculares, por lo que hay un plano en el que la dislocación puede deslizarse.

Trepar

El ascenso por dislocación es un mecanismo alternativo de movimiento de dislocación que permite que una dislocación de borde se mueva fuera de su plano de deslizamiento. La fuerza impulsora del ascenso por dislocación es el movimiento de las vacantes a través de una red cristalina. Si una vacante se mueve junto al límite del semiplano adicional de átomos que forma una dislocación de borde, el átomo en el semiplano más cercano a la vacante puede saltar y llenar la vacante. Este desplazamiento atómico mueve la vacante en línea con el semiplano de átomos, lo que provoca un desplazamiento, o ascenso positivo, de la dislocación. El proceso de absorción de una vacante en el límite de un semiplano de átomos, en lugar de crearse, se conoce como ascenso negativo. Dado que el ascenso por dislocación resulta de átomos individuales que saltan a las vacantes, el ascenso se produce en incrementos de diámetro de un solo átomo.

Durante el ascenso positivo, el cristal se encoge en la dirección perpendicular al semiplano adicional de átomos porque se están eliminando átomos del semiplano. Dado que el ascenso negativo implica una adición de átomos al semiplano, el cristal crece en la dirección perpendicular al semiplano. Por lo tanto, la tensión de compresión en la dirección perpendicular al semiplano promueve el ascenso positivo, mientras que la tensión de tracción promueve el ascenso negativo. Esta es una de las principales diferencias entre deslizamiento y ascenso, ya que el deslizamiento es causado únicamente por la tensión de corte.

Otra diferencia entre el deslizamiento por dislocación y el ascenso es la dependencia de la temperatura. El ascenso se produce mucho más rápidamente a temperaturas altas que a temperaturas bajas debido a un aumento del movimiento de vacancia. El deslizamiento, por otro lado, tiene una dependencia pequeña de la temperatura.

Avalanchas de dislocación

Las avalanchas de dislocaciones ocurren cuando se producen múltiples movimientos simultáneos de dislocaciones.

Velocidad de dislocación

La velocidad de dislocación depende en gran medida de la tensión cortante y la temperatura, y a menudo se puede ajustar utilizando una función de ley de potencia: ^[14]

${\displaystyle v=A\tau ^{m}}$

donde es una constante del material, es la tensión de corte aplicada, es una constante que disminuye con el aumento de la temperatura. El aumento de la tensión de corte aumentará la velocidad de dislocación, mientras que el aumento de la temperatura normalmente disminuirá la velocidad de dislocación. Se plantea la hipótesis de que una mayor dispersión de fonones a temperaturas más altas es responsable del aumento de las fuerzas de amortiguación que ralentizan el movimiento de la dislocación. ${\displaystyle A}$ ${\displaystyle \tau }$ ${\displaystyle m}$

Geometría

Una dislocación de borde (b = vector de Burgers )

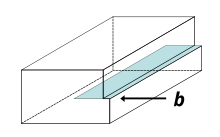
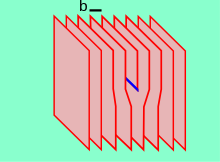
Existen dos tipos principales de dislocaciones móviles: de borde y de tornillo. Las dislocaciones que se encuentran en los materiales reales suelen ser mixtas , es decir, tienen características de ambas.

Borde

Diagrama esquemático (planos reticulares) que muestra una dislocación de arista. El vector de Burgers está en negro y la línea de dislocación en azul.

Un material cristalino está formado por una matriz regular de átomos, dispuestos en planos reticulares. Una dislocación de borde es un defecto en el que se introduce un semiplano adicional de átomos en la mitad del cristal, distorsionando los planos de átomos cercanos. Cuando se aplica suficiente fuerza desde un lado de la estructura cristalina, este plano adicional pasa a través de planos de átomos rompiendo y uniendo enlaces con ellos hasta que alcanza el límite de grano. La dislocación tiene dos propiedades: una dirección de línea, que es la dirección que corre a lo largo de la parte inferior del semiplano adicional, y el vector de Burgers , que describe la magnitud y la dirección de la distorsión en la red. En una dislocación de borde, el vector de Burgers es perpendicular a la dirección de la línea.

Las tensiones provocadas por una dislocación de borde son complejas debido a su asimetría inherente. Estas tensiones se describen mediante tres ecuaciones: ^[15]

${\displaystyle \sigma _{xx}={\frac {-\mu \mathbf {b} }{2\pi (1-\nu )}}{\frac {y(3x^{2}+y^{2})}{(x^{2}+y^{2})^{2}}}}$

${\displaystyle \sigma _{yy}={\frac {\mu \mathbf {b} }{2\pi (1-\nu )}}{\frac {y(x^{2}-y^{2})}{(x^{2}+y^{2})^{2}}}}$

${\displaystyle \tau _{xy}={\frac {\mu \mathbf {b} }{2\pi (1-\nu )}}{\frac {x(x^{2}-y^{2})}{(x^{2}+y^{2})^{2}}}}$

donde es el módulo de corte del material, es el vector de Burgers , es el coeficiente de Poisson y y son coordenadas. ${\displaystyle \mu }$ ${\displaystyle \mathbf {b} }$ ${\displaystyle \nu }$ ${\displaystyle x}$ ${\displaystyle y}$

Estas ecuaciones sugieren una pesa de tensiones orientada verticalmente que rodea la dislocación, con compresión experimentada por los átomos cerca del plano "extra" y tensión experimentada por los átomos cerca del plano "faltante". ^[15]

Tornillo

Una dislocación helicoidal se puede visualizar cortando un cristal a lo largo de un plano y deslizando una mitad a través de la otra mediante un vector reticular, de modo que las mitades vuelvan a encajar sin dejar un defecto. Si el corte solo atraviesa parcialmente el cristal y luego se desliza, el límite del corte es una dislocación helicoidal. Comprende una estructura en la que los planos atómicos de la red cristalina trazan una trayectoria helicoidal alrededor del defecto lineal (línea de dislocación). En las dislocaciones helicoidales puras, el vector de Burgers es paralelo a la dirección de la línea. ^[16] Una serie de dislocaciones helicoidales puede provocar lo que se conoce como un límite de torsión. En un límite de torsión, la desalineación entre los granos de cristal adyacentes se produce debido al efecto acumulativo de las dislocaciones helicoidales dentro del material. Estas dislocaciones provocan una desorientación rotacional entre los granos adyacentes, lo que conduce a una deformación similar a una torsión a lo largo del límite. Los límites de torsión pueden influir significativamente en las propiedades mecánicas y eléctricas de los materiales, afectando fenómenos como el deslizamiento de los límites de grano, la fluencia y el comportamiento de fractura ^[17]. Las tensiones causadas por una dislocación de tornillo son menos complejas que las de una dislocación de borde y solo necesitan una ecuación, ya que la simetría permite utilizar una coordenada radial: ^[15]

${\displaystyle \tau _{r}={\frac {-\mu \mathbf {b} }{2\pi r}}}$

donde es el módulo de corte del material, es el vector de Burgers y es una coordenada radial. Esta ecuación sugiere un cilindro largo de tensión que irradia hacia afuera desde el cilindro y disminuye con la distancia. Este modelo simple da como resultado un valor infinito para el núcleo de la dislocación en y, por lo tanto, solo es válido para tensiones fuera del núcleo de la dislocación. ^[15] Si el vector de Burgers es muy grande, el núcleo puede estar realmente vacío, lo que da como resultado un microtubo , como se observa comúnmente en el carburo de silicio . ${\displaystyle \mu }$ ${\displaystyle \mathbf {b} }$ ${\displaystyle r}$ ${\displaystyle r=0}$

Mezclado

En muchos materiales se encuentran dislocaciones en las que la dirección de la línea y el vector de Burgers no son ni perpendiculares ni paralelos y estas dislocaciones se denominan dislocaciones mixtas , que consisten tanto en un tornillo como en un borde. Se caracterizan por , el ángulo entre la dirección de la línea y el vector de Burgers, donde para dislocaciones de borde puras y para dislocaciones de tornillo. ${\displaystyle \varphi }$ ${\displaystyle \varphi =\pi /2}$ ${\displaystyle \varphi =0}$

Parcial

Las dislocaciones parciales dejan una falla de apilamiento. Hay dos tipos de dislocaciones parciales: la dislocación parcial de Frank , que es sésil, y la dislocación parcial de Shockley , que es deslizante. ^[3]

Una dislocación parcial de Frank se forma al insertar o eliminar una capa de átomos en el plano {111}, que luego está delimitado por la dislocación parcial de Frank. La eliminación de una capa compacta se conoce como falla de apilamiento intrínseca y la inserción de una capa se conoce como falla de apilamiento extrínseca . El vector de Burgers es normal al plano de deslizamiento {111}, por lo que la dislocación no puede deslizarse y solo puede moverse mediante ascenso . ^[1]

Para reducir la energía total de la red, las dislocaciones de borde y de tornillo generalmente se disocian en una falla de apilamiento limitada por dos dislocaciones parciales de Shockley. ^[18] El ancho de esta región de falla de apilamiento es proporcional a la energía de falla de apilamiento del material. El efecto combinado se conoce como dislocación extendida y puede deslizarse como una unidad. Sin embargo, las dislocaciones de tornillo disociadas deben recombinarse antes de poder deslizarse de forma cruzada , lo que dificulta que estas dislocaciones se desplacen alrededor de las barreras. Los materiales con bajas energías de falla de apilamiento tienen la mayor disociación de dislocación y, por lo tanto, se trabajan en frío con mayor facilidad.

La vía de acceso y el cruce Lomer-Cottrell

Si dos dislocaciones de deslizamiento que se encuentran en diferentes planos {111} se dividen en parciales de Shockley y se intersecan, producirán una dislocación de barra de escalera con una dislocación de Lomer-Cottrell en su vértice. ^[19] Se llama barra de escalera porque es análoga a la barra que mantiene la alfombra en su lugar en una escalera.

Sacudida

Diferencias geométricas entre quiebros y curvas

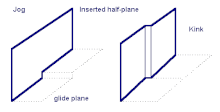
Un jog describe los pasos de una línea de dislocación que no están en el plano de deslizamiento de una estructura cristalina . ^[18] Una línea de dislocación rara vez es uniformemente recta, a menudo contiene muchas curvas y pasos que pueden impedir o facilitar el movimiento de la dislocación al actuar como puntos de precisión o puntos de nucleación respectivamente. Debido a que los jogs están fuera del plano de deslizamiento, bajo cizallamiento no pueden moverse por deslizamiento (movimiento a lo largo del plano de deslizamiento). En cambio, deben confiar en el ascenso facilitado por difusión de vacantes para moverse a través de la red. ^[20] Lejos del punto de fusión de un material, la difusión de vacantes es un proceso lento, por lo que los jogs actúan como barreras inmóviles a temperatura ambiente para la mayoría de los metales. ^[21]

Los desniveles se forman típicamente cuando dos dislocaciones no paralelas se cruzan durante el deslizamiento. La presencia de desniveles en un material aumenta su límite elástico al evitar el deslizamiento fácil de las dislocaciones. Un par de desniveles inmóviles en una dislocación actuará como una fuente de Frank-Read bajo cizallamiento, aumentando la densidad general de dislocaciones de un material. ^[21] Cuando el límite elástico de un material aumenta a través del aumento de la densidad de dislocaciones, particularmente cuando se hace mediante trabajo mecánico, se denomina endurecimiento por deformación . A altas temperaturas, el movimiento de desniveles facilitado por vacantes se convierte en un proceso mucho más rápido, lo que disminuye su eficacia general para impedir el movimiento de las dislocaciones.

Pliegue

Las torceduras son escalones en una línea de dislocación paralelos a los planos de deslizamiento. A diferencia de los recovecos, facilitan el deslizamiento al actuar como un punto de nucleación para el movimiento de dislocación. La propagación lateral de una torcedura desde el punto de nucleación permite la propagación hacia adelante de la dislocación mientras se mueven solo unos pocos átomos a la vez, lo que reduce la barrera de energía general al deslizamiento.

Ejemplo en dos dimensiones (2D)

Disociación de un par de dislocaciones debido al cizallamiento (flechas rojas) de un cristal hexagonal en 2D. Una dislocación en 2D consiste en un par ligado de números de coordinación quíntuple (verde) y séptuple (naranja).

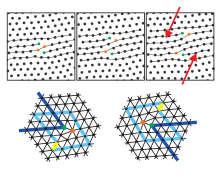
En dos dimensiones (2D) sólo existen las dislocaciones de borde, que desempeñan un papel central en la fusión de cristales 2D, pero no la dislocación helicoidal. Esas dislocaciones son defectos puntuales topológicos , lo que implica que no pueden crearse de forma aislada mediante una transformación afín sin cortar el cristal hexagonal hasta el infinito (o al menos hasta su borde). Sólo pueden crearse en pares con vector de Burgers antiparalelo . Si se excitan térmicamente muchas dislocaciones, por ejemplo, se destruye el orden de traslación discreto del cristal. Simultáneamente, desaparecen el módulo de corte y el módulo de Young , lo que implica que el cristal se funde en una fase fluida. El orden orientacional aún no se destruye (como lo indican las líneas reticulares en una dirección) y se encuentra -muy similar a los cristales líquidos- una fase fluida con un campo director típicamente séxtuple. Esta denominada fase hexática todavía tiene una rigidez orientacional. La fase de fluido isótropo aparece si las dislocaciones se disocian en disclinaciones aisladas de cinco y siete pliegues . ^[22] Esta fusión en dos pasos se describe dentro de la llamada teoría de Kosterlitz-Thouless-Halperin-Nelson-Young ( teoría KTHNY ), basada en dos transiciones de tipo Kosterlitz-Thouless .

Observación

Microscopía electrónica de transmisión (MET)

Micrografía electrónica de transmisión de dislocaciones.

Micrografía electrónica de transmisión de dislocaciones.

La microscopía electrónica de transmisión se puede utilizar para observar dislocaciones dentro de la microestructura del material. ^[23] Se preparan láminas delgadas de material para que sean transparentes al haz de electrones del microscopio. El haz de electrones sufre difracción por los planos regulares de la red cristalina en un patrón de difracción y se genera contraste en la imagen por esta difracción (así como por variaciones de espesor, variación de la tensión y otros mecanismos). Las dislocaciones tienen una estructura atómica local diferente y producen un campo de tensión, y por lo tanto harán que los electrones en el microscopio se dispersen de diferentes maneras. Observe el contraste "ondulado" característico de las líneas de dislocación a medida que pasan a través del espesor del material en la figura (las dislocaciones no pueden terminar en un cristal, y estas dislocaciones terminan en las superficies ya que la imagen es una proyección 2D).

Las dislocaciones no tienen estructuras aleatorias, la estructura atómica local de una dislocación está determinada por el vector de Burgers. Una aplicación muy útil del TEM en la obtención de imágenes de dislocaciones es la capacidad de determinar experimentalmente el vector de Burgers. La determinación del vector de Burgers se logra mediante lo que se conoce como análisis ("g punto b"). ^[24] Al realizar una microscopía de campo oscuro con el TEM, se selecciona un punto difractado para formar la imagen (como se mencionó anteriormente, los planos reticulares difractan el haz en puntos), y la imagen se forma utilizando solo electrones que fueron difractados por el plano responsable de ese punto de difracción. El vector en el patrón de difracción desde el punto transmitido hasta el punto difractado es el vector. El contraste de una dislocación se escala por un factor del producto escalar de este vector y el vector de Burgers ( ). Como resultado, si el vector de Burgers y el vector son perpendiculares, no habrá señal de la dislocación y la dislocación no aparecerá en absoluto en la imagen. Por lo tanto, al examinar diferentes imágenes de campo oscuro formadas a partir de puntos con diferentes vectores g, se puede determinar el vector de Burgers. ${\displaystyle {\vec {g}}\cdot {\vec {b}}}$ ${\displaystyle {\vec {g}}}$ ${\displaystyle {\vec {g}}\cdot {\vec {b}}}$ ${\displaystyle {\vec {g}}}$

Otros métodos

Fosas de grabado formadas en los extremos de las dislocaciones en silicio, orientación (111)

La microscopía de iones de campo y las técnicas de sonda atómica ofrecen métodos para producir aumentos mucho mayores (normalmente 3 millones de veces o más) y permiten la observación de dislocaciones a nivel atómico. Cuando el relieve de la superficie se puede resolver al nivel de un escalón atómico, las dislocaciones en espiral aparecen como características espirales distintivas, lo que revela un mecanismo importante de crecimiento del cristal: donde hay un escalón superficial, los átomos pueden agregarse más fácilmente al cristal, y el escalón superficial asociado con una dislocación en espiral nunca se destruye, sin importar cuántos átomos se le agreguen.

Grabado químico

Cuando una línea de dislocación intersecta la superficie de un material metálico, el campo de deformación asociado aumenta localmente la susceptibilidad relativa del material al ataque ácido y se produce una picadura de ataque con un formato geométrico regular. De esta manera, las dislocaciones en el silicio, por ejemplo, se pueden observar indirectamente utilizando un microscopio de interferencia. La orientación del cristal se puede determinar por la forma de las picadura de ataque asociadas con las dislocaciones.

Si el material se deforma y se graba nuevamente en repetidas ocasiones, se puede producir una serie de hoyos de grabado que rastrean efectivamente el movimiento de la dislocación en cuestión.

Fuerzas de dislocación

Fuerzas sobre dislocaciones

El movimiento de dislocación como resultado de la tensión externa sobre una red cristalina se puede describir utilizando fuerzas internas virtuales que actúan perpendicularmente a la línea de dislocación. La ecuación de Peach-Koehler ^{[25] [26] [27]} se puede utilizar para calcular la fuerza por unidad de longitud sobre una dislocación en función del vector de Burgers, , la tensión, , y el vector de sentido, . ${\displaystyle \mathbf {b} }$ ${\displaystyle \sigma }$ ${\displaystyle \mathbf {s} }$

${\displaystyle \mathbf {f} =(\mathbf {b} \cdot \sigma )\times \mathbf {s} }$

La fuerza por unidad de longitud de dislocación es una función del estado general de tensión, , y del vector de sentido, . ${\displaystyle \mathbf {F} }$ ${\displaystyle \mathbf {s} }$

${\displaystyle \mathbf {f} =\mathbf {F} \times \mathbf {s} ={\begin{vmatrix}{\hat {\imath }}&{\hat {\jmath }}&{\hat {k}}\\F_{x}&F_{y}&F_{z}\\s_{x}&s_{y}&s_{z}\end{vmatrix}}}$

Los componentes del campo de tensiones se pueden obtener a partir del vector de Burgers, las tensiones normales, , y las tensiones cortantes, . ${\displaystyle \sigma }$ ${\displaystyle \tau }$

${\displaystyle {\begin{aligned}F_{x}&=b_{x}\sigma _{xx}+b_{y}\tau _{xy}+b_{z}\tau _{xz}\\F_{y}&=b_{x}\tau _{yx}+b_{y}\sigma _{yy}+b_{z}\tau _{yz}\\F_{z}&=b_{x}\tau _{zx}+b_{y}\tau _{zy}+b_{z}\sigma _{zz}\end{aligned}}}$

Fuerzas entre dislocaciones

La fuerza entre dislocaciones se puede derivar de la energía de las interacciones de las dislocaciones, . El trabajo realizado al desplazar las caras cortadas paralelas a un eje elegido crea una dislocación en el campo de tensión de otro desplazamiento. Para las direcciones y : ${\displaystyle U_{\rm {int}}}$ ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle {\begin{aligned}U_{\rm {int}}&=\int _{x}^{\infty }(b_{x}\tau _{xy}+b_{y}\sigma _{yy}+b_{z}\sigma _{zy})\,dx\\U_{\rm {int}}&=\int _{y}^{\infty }(b_{x}\sigma _{xx}+b_{y}\tau _{yx}+b_{z}\sigma _{zx})\,dy\end{aligned}}}$

Las fuerzas se encuentran entonces tomando las derivadas.

${\displaystyle {\begin{aligned}F_{x}&=-{\frac {\partial U_{\rm {int}}}{\partial x}}\\F_{y}&=-{\frac {\partial U_{\rm {int}}}{\partial y}}\end{aligned}}}$

Fuerzas de superficie libre

Las dislocaciones también tenderán a desplazarse hacia superficies libres debido a la menor energía de deformación. Esta fuerza ficticia se puede expresar para una dislocación de tornillo con el componente igual a cero como: ${\displaystyle y}$

${\displaystyle F_{x}=b\tau _{zy}=-{\frac {Gb^{2}}{4\pi d}}}$

donde es la distancia desde la superficie libre en la dirección. La fuerza para una dislocación de borde con se puede expresar como: ${\displaystyle d}$ ${\displaystyle x}$ ${\displaystyle y=0}$

${\displaystyle F_{x}=b\tau _{xy}=-{\frac {Gb^{2}}{4\pi (1-\nu )d}}}$

Referencias

1. Hull, D.; Bacon, DJ (2001). Introducción a las dislocaciones (4.ª ed.). Butterworth-Heinemann. doi :10.1016/B978-0-7506-4681-9.X5000-7. ISBN 978-0-7506-4681-9.
2. Anderson, Peter M.; Hirth, John Price; Lothe, Jens (2017). Teoría de dislocaciones (tercera edición). Nueva York, NY: Cambridge University Press. ISBN 978-0-521-86436-7.OCLC 950750996  .
3. "Dislocaciones en materiales de FCC". 24 de mayo de 2014. Consultado el 8 de noviembre de 2019 .
4. Vito Volterra (1907) "Sur l'équilibre des corps élastiques multiplement connexes", Annales Scientifiques de l'École Normale Supérieure , vol. 24, págs. 401–517
5. GI Taylor (1934). "El mecanismo de deformación plástica de los cristales. Parte I. Teórica". Actas de la Royal Society de Londres. Serie A . 145 (855): 362–87. Bibcode :1934RSPSA.145..362T. doi : 10.1098/rspa.1934.0106 . JSTOR  2935509.
6. Marc André Meyers , Krishan Kumar Chawla (1999) Comportamientos mecánicos de los materiales. Prentice Hall, págs. 228-31, ISBN 0132628171 . 
7. Schober, T.; Balluffi, RW (1 de enero de 1970). "Observación cuantitativa de matrices de dislocaciones desadaptadas en límites de grano de torsión de ángulos bajos y altos". Revista filosófica . 21 (169): 109–123. Bibcode :1970PMag...21..109S. doi :10.1080/14786437008238400. ISSN  0031-8086.
8. Eyre, BL (febrero de 1973). "Estudios con microscopio electrónico de transmisión de cúmulos de defectos puntuales en metales fcc y bcc". Journal of Physics F: Metal Physics . 3 (2): 422–470. Bibcode :1973JPhF....3..422E. doi :10.1088/0305-4608/3/2/009. ISSN  0305-4608.
9. Masters, BC (1965-05-01). "Bucles de dislocación en hierro irradiado". Revista filosófica . 11 (113): 881–893. Bibcode :1965PMag...11..881M. doi :10.1080/14786436508223952. ISSN  0031-8086. S2CID  4205189.
10. Kirk, MA; Robertson, IM; Jenkins, ML; English, CA; Black, TJ; Vetrano, JS (1987-06-01). "El colapso de las cascadas de defectos en bucles de dislocación". Journal of Nuclear Materials . 149 (1): 21–28. Bibcode :1987JNuM..149...21K. doi :10.1016/0022-3115(87)90494-6. ISSN  0022-3115.
11. Suresh, S. (2004). Fatiga de materiales . Cambridge University Press. ISBN 978-0-521-57046-6.
12. Forsythe, PJE (1953). "Exudación de material de las bandas de deslizamiento en la superficie de cristales fatigados de una aleación de aluminio y cobre". Nature . 171 (4343): 172–173. Bibcode :1953Natur.171..172F. doi :10.1038/171172a0. S2CID  4268548.
13. Grundmann, Marius (2010). La física de los semiconductores: una introducción que incluye nanofísica y aplicaciones (2.ª ed.). Springer. pág. 87. ISBN 978-3-642-13883-6.
14. Soboyejo, Wole (2003). "7.3 Velocidad de dislocación". Propiedades mecánicas de materiales de ingeniería . Marcel Dekker. ISBN 0-8247-8900-8.OCLC 300921090  .
15. Reed-Hill, RE; Abbaschian, Reza (1994). Principios de metalurgia física . Boston: PWS Publishing Company. ISBN 0-534-92173-6.
16. James Shackelford (2009). Introducción a la ciencia de los materiales para ingenieros (7.ª ed.). Upper Saddle River, Nueva Jersey: Pearson Prentice Hall. pp. 110–11. ISBN 978-0-13-601260-3.
17. James Shackelford (2009). Introducción a la ciencia de los materiales para ingenieros (7.ª ed.). Upper Saddle River, Nueva Jersey: Pearson Prentice Hall. pp. 110–11. ISBN 978-0-13-601260-3.
18. Föll, Helmut. "Defectos en los cristales" . Consultado el 9 de noviembre de 2019 .
19. "Reacción que forma una dislocación en forma de barra de escalera" . Consultado el 26 de noviembre de 2019 .
20. Cai, W.; Nix, WD (2016). Imperfecciones en sólidos cristalinos . Cambridge, Reino Unido: Cambridge University Press.
21. Courtney, TH (2000). Comportamiento mecánico de los materiales . Long Grove, IL: Waveland.
22. Gasser, U.; Eisenmann, C.; Maret, G.; Keim, P. (2010). "Fusión de cristales en dos dimensiones". ChemPhysChem . 11 (5): 963–970. doi :10.1002/cphc.200900755. PMID  20099292.
23. Spence, JCH ; et al. (2006). "Obtención de imágenes de núcleos de dislocación: el camino a seguir". Philosophical Magazine . 86 (29–31): 4781–4796. Bibcode :2006PMag...86.4781S. doi :10.1080/14786430600776322. S2CID  135976739.
24. Williams, David B.; Carter, C. Barry (2008). Microscopía electrónica de transmisión: un libro de texto para la ciencia de los materiales . Springer. ISBN 9780387765020.OCLC 660999227  .
25. Peach, M.; Koehler, JS (1950-11-01). "Las fuerzas ejercidas sobre las dislocaciones y los campos de tensión producidos por ellas". Physical Review . 80 (3): 436–439. Bibcode :1950PhRv...80..436P. doi :10.1103/PhysRev.80.436.
26. Suzuki, Taira (1991). Dinámica de dislocación y plasticidad . Takeuchi, Shin., Yoshinaga, Hideo. Berlín, Heidelberg: Springer Berlin Heidelberg. pág. 8. ISBN. 978-3-642-75774-7.OCLC 851741787  .
27. Soboyejo, Winston O. (2003). "6 Introducción a la mecánica de dislocaciones". Propiedades mecánicas de materiales de ingeniería . Nueva York: Marcel Dekker. ISBN 0-8247-8900-8.OCLC 50868191  .

Enlaces externos

• Defectos en los cristales/ Sitio web del Prof. Dr. Helmut Föll El capítulo 5 contiene una gran cantidad de información sobre dislocaciones;
• Tutorial en línea de DoITPoMS sobre dislocaciones, que incluye películas de dislocaciones en balsas de burbujas ;
• Diferencia entre dislocación de borde y dislocación de tornillo Diferencia entre dislocación de borde y dislocación de tornillo en detalle;
• Microscopio de efecto túnel – Galería Galería de imágenes, incluyendo una página de dislocaciones, vistas a nivel atómico de superficies metálicas, por el grupo de física de superficies de la Facultad de Física, Universidad Tecnológica de Viena, Austria.
• Volterra, V., "Sobre el equilibrio de los cuerpos multiconexos", trad. de DH Delphenich
• Somigliana, C., "Sobre la teoría de las distorsiones elásticas", trad. de DH Delphenich