Teoría KTHNY

La teoría KTHNY describe la fusión de cristales en dos dimensiones (2D). El nombre se deriva de las iniciales de los apellidos de John Michael Kosterlitz , David J. Thouless , ^{[1] [2]} Bertrand Halperin , David R. Nelson , ^{[3] [4]} y A. Peter Young, ^[5] quienes desarrolló la teoría en la década de 1970. Es, junto al modelo de Ising en 2D y el modelo XY en 2D, ^{[6] [7]} una de las pocas teorías que se puede resolver analíticamente y que predice una transición de fase a una temperatura . ${\displaystyle T>0}$

Idea principal

La fusión de cristales 2D está mediada por la disociación de defectos topológicos , que destruyen el orden del cristal. En 2016, Michael Kosterlitz y David Thouless recibieron el Premio Nobel de Física por su idea de cómo pares de dislocaciones virtuales excitadas térmicamente inducen un ablandamiento (descrito por la teoría de grupos de renormalización ) del cristal durante el calentamiento. La elasticidad al corte desaparece simultáneamente con la disociación de las dislocaciones, lo que indica una fase fluida. ^{[8] [9]} Basándose en este trabajo, David Nelson y Bertrand Halperin demostraron que la fase hexática resultante aún no es un fluido isotrópico. A partir de un cristal hexagonal (que es la estructura empaquetada más densa en 2D), la fase hexática tiene un campo director séxtuple, similar a los cristales líquidos. El orden orientativo sólo desaparece debido a las disociaciones de una segunda clase de defectos topológicos, denominadas disclinaciones . Peter Young calculó el exponente crítico de la longitud de las correlaciones divergentes en la transición entre cristalino y hexático. La teoría KTHNY predice dos transiciones de fase continuas , por lo que se descarta la coexistencia de fase y calor latente. Las fases termodinámicas se pueden distinguir según el orden de traslación y orientación discreto versus continuo. Una de las transiciones separa una fase sólida con un orden de traslación de casi largo alcance y un orden de orientación perfecto de largo alcance de la fase hexática. La fase hexática muestra un orden de traducción de corto alcance y un orden de orientación de casi largo alcance. La segunda transición de fase separa la fase hexática del fluido isotrópico, donde tanto el orden de traslación como el de orientación son de corto alcance. El sistema está dominado por fluctuaciones críticas, ya que para transiciones continuas, la diferencia de energía entre las fases termodinámicas desaparece en las proximidades de la transición. Esto implica que las regiones ordenadas y desordenadas fluctúan fuertemente en el espacio y el tiempo. El tamaño de esas regiones crece fuertemente cerca de las transiciones y diverge en la transición misma. En este punto, el patrón de simetría rota frente a dominios simétricos es fractal . Los fractales se caracterizan por una invariancia de escala: parecen similares en una escala arbitraria o al acercarse arbitrariamente (esto es cierto en cualquier escala mayor que la distancia atómica). La invariancia de escala es la base para utilizar la teoría del grupo de renormalización para describir las transiciones de fase. Ambas transiciones van acompañadas de una ruptura espontánea de la simetría.. A diferencia de la fusión en tres dimensiones, la ruptura de la simetría traslacional y orientacional no necesita aparecer simultáneamente en 2D, ya que dos tipos diferentes de defectos topológicos destruyen los diferentes tipos de orden.

Fondo

Michael Kosterlitz y David Thouless intentaron resolver una contradicción sobre los cristales 2D: por un lado, el teorema de Mermin-Wagner afirma que la ruptura de simetría de un parámetro de orden continuo no puede existir en dos dimensiones. Esto implica que el orden posicional perfecto de largo alcance se descarta en cristales 2D. Por otro lado, las primeras simulaciones por computadora de Berni Alder y Thomas E. Wainwright indicaron cristalización en 2D. La teoría KTHNY muestra implícitamente que la periodicidad no es un criterio necesario para un sólido (esto ya lo indica la existencia de sólidos amorfos como los vidrios). Siguiendo a M. Kosterlitz, una elasticidad de corte finita define un sólido 2D, incluidos los cuasicristales en esta descripción.

Factor de estructura en 2D

Figura 1: Factor de estructura de a) un fluido isotrópico, b) la fase hexática, c) un cristal en dos dimensiones.

Las tres fases termodinámicas y sus correspondientes simetrías se pueden visualizar utilizando el factor de estructura : . La doble suma abarca todas las posiciones de los pares de partículas i y j y los corchetes indican un promedio de varias configuraciones. La fase isotrópica se caracteriza por anillos concéntricos en , si la distancia promedio de las partículas se calcula mediante la densidad de partículas 2D . La fase cristalina (empaquetada cerrada) se caracteriza por una simetría séxtuple basada en el orden de orientación. A diferencia del 3D, donde los picos son arbitrariamente agudos ( picos), los picos 2D tienen un ancho finito descrito con una curva de Lorenz. Esto se debe al hecho de que el orden de traslación tiene un alcance casi largo como lo predice el teorema de Mermin-Wagner. La fase hexática se caracteriza por seis segmentos, que reflejan el orden de orientación de rango casi largo. El factor de estructura de la Figura 1 se calcula a partir de las posiciones de una monocapa coloidal (los cruces de alta intensidad son artefactos de la transformación de Fourier debido al campo de visión finito (rectangular) del conjunto). ${\displaystyle S({\vec {q}})={\frac {1}{N}}\langle \sum _{ij}e^{-i{\vec {q}}({\vec {r}}_{i}-{\vec {r}}_{j})}\rangle }$ ${\displaystyle q=2\pi /a}$ ${\displaystyle a=1/{\sqrt {\rho }}}$ ${\displaystyle \rho }$ ${\displaystyle \delta }$

Interacción entre dislocaciones.

Figura 2: Si el módulo de Young se vuelve , la elasticidad desaparece de forma discontinua y el cristal se funde. ${\displaystyle 16\pi }$

Para analizar la fusión debida a la disociación de dislocaciones, se comienza con la energía en función de la distancia entre dos dislocaciones. Una dislocación aislada en 2D es una distorsión local de la red séxtuple, donde las partículas vecinas tienen cinco y siete vecinos más cercanos, en lugar de seis. Es importante señalar que las dislocaciones sólo se pueden crear en pares, por razones topológicas. Un par de dislocaciones ligadas es una configuración local con vecindad 5-7-7-5. ${\displaystyle H_{loc}}$

${\displaystyle H_{loc}=-{\frac {a^{2}Y}{8\pi }}\sum _{k\neq l}{\Big [}{\vec {b}}({\vec {r}}_{k})\cdot {\vec {b}}({\vec {r}}_{l})\ln {\frac {\Delta {\vec {r}}_{k,l}}{a}}-{\frac {[{\vec {b}}({\vec {r}}_{k})\cdot \Delta {\vec {r}}_{k,l}][{\vec {b}}({\vec {r}}_{l})\cdot \Delta {\vec {r}}_{k,l}]}{\Delta r_{i,j}^{2}}}{\Big ]}+E_{c}\cdot N_{loc}.}$

La doble suma recorre todas las posiciones de los pares de defectos y mide la distancia entre las dislocaciones. es el vector de Burgers y denota la orientación de la dislocación en la posición Orte . El segundo término entre paréntesis trae dislocaciones que se disponen preferentemente en antiparalelo por razones energéticas. Su contribución es pequeña y puede despreciarse cuando la distancia entre defectos es grande. La principal contribución proviene del término logarítmico (el primero entre paréntesis) que describe cómo la energía de un par de dislocaciones diverge al aumentar la distancia. Dado que la distancia más corta entre dos dislocaciones viene dada aproximadamente por la distancia promedio de las partículas , la escala de distancias evita que el logaritmo se vuelva negativo. La fuerza de la interacción es proporcional al módulo de Young dado por la rigidez de la red cristalina. Para crear una dislocación a partir de una red no perturbada, se necesita un pequeño desplazamiento en una escala menor que la distancia promedio de las partículas . La energía discreta asociada con este desplazamiento generalmente se denomina energía central Energie y debe contarse para cada una de las dislocaciones individualmente (último término). ${\displaystyle k}$ ${\displaystyle l}$ ${\displaystyle \Delta {\vec {r}}_{k,l}={\vec {r}}_{k}-{\vec {r}}_{l}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {r}}_{k}}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle \ln {\frac {\Delta {\vec {r}}_{k,l}}{a}}}$ ${\displaystyle Y}$ ${\displaystyle a}$ ${\displaystyle E_{c}}$ ${\displaystyle N_{loc}}$

Un argumento fácil a favor del término logarítmico dominante es que la magnitud de la deformación inducida por una dislocación aislada decae según la distancia. Suponiendo la aproximación de Hooke , la tensión asociada es lineal con la deformación. Al integrar la deformación ~1/r se obtiene la energía proporcional al logaritmo. La dependencia logarítmica de la energía con la distancia es la razón por la que la teoría KTHNY es una de las pocas teorías de transiciones de fase que se puede resolver analíticamente: en física estadística hay que calcular funciones de partición , por ejemplo, la distribución de probabilidad para todas las configuraciones posibles de dislocación. pares dados por la distribución de Boltzmann . Aquí está la energía térmica con constante de Boltzmann . Para la mayoría de los problemas de física estadística es difícil resolver la función de partición debido a la enorme cantidad de partículas y grados de libertad. Esto es diferente en la teoría KTHNY debido a las funciones de energía logarítmicas de las dislocaciones y la función e del factor de Boltzmann como inversa que se puede resolver fácilmente. ${\displaystyle \propto {\frac {1}{r}}}$ ${\displaystyle e^{\frac {H_{loc}}{k_{B}T}}}$ ${\displaystyle k_{B}T}$ ${\displaystyle k_{B}}$ ${\displaystyle H_{loc}}$

Ejemplo

Queremos calcular la distancia media al cuadrado entre dos dislocaciones considerando solo el término logarítmico dominante por simplicidad:

${\displaystyle \langle r^{2}\rangle ={\frac {\int r^{2}\cdot e^{-{\frac {Ya\ln(r/a)}{4\pi k_{B}T}}}d^{2}r}{\int e^{-{\frac {Ya\ln(r/a)}{4\pi k_{B}T}}}d^{2}r}}\sim {\frac {2-{\frac {Y\cdot a}{4\pi k_{B}T}}}{4-{\frac {Y\cdot a}{4\pi k_{B}T}}}}.}$

Esta distancia media tiende a cero a bajas temperaturas: las dislocaciones se aniquilarán y el cristal quedará libre de defectos. La expresión diverge , si el denominador tiende a cero. Esto sucede, cuando . Una distancia divergente de las dislocaciones implica que están disociadas y no forman un par unido. El cristal se funde si se excitan térmicamente varias dislocaciones aisladas y la temperatura de fusión viene dada por el módulo de Young: ${\displaystyle \langle r^{2}\rangle \to 0}$ ${\displaystyle \langle r^{2}\rangle \to \infty }$ ${\displaystyle {\frac {Y\cdot a}{4\pi k_{B}T}}=4}$ ${\displaystyle T_{m}}$

${\displaystyle {\frac {Y\cdot a}{k_{B}T_{m}}}=16\pi .}$

La cantidad adimensional es una constante universal para la fusión en 2D y es independiente de los detalles del sistema bajo investigación. Este ejemplo investigó sólo un par aislado de dislocaciones. En general, durante la fusión aparecerán múltiples dislocaciones. El campo de deformación de una dislocación aislada quedará protegido y el cristal se ablandará en las proximidades de la transición de fase; El módulo de Young disminuirá debido a las dislocaciones. En la teoría KTHNY, esta retroalimentación de las dislocaciones sobre la elasticidad, y especialmente sobre el módulo de Young que actúa como constante de acoplamiento en la función de energía, se describe en el marco de la teoría de grupos de renormalización . ${\displaystyle 16\pi }$

Renormalización de la elasticidad.

Si se calienta un cristal 2D, se excitarán pares de dislocaciones virtuales debido a fluctuaciones térmicas en las proximidades de la transición de fase. Virtual significa que la energía térmica promedio no es lo suficientemente grande como para superar (dos veces) la energía del núcleo y disociar (desvincular) los pares de dislocaciones. Sin embargo, los pares de dislocaciones pueden aparecer localmente en escalas de tiempo muy cortas debido a fluctuaciones térmicas, antes de aniquilarse nuevamente. Aunque aniquilan, tienen un impacto detectable sobre la elasticidad: ablandan el cristal. El principio es completamente análogo al cálculo de la carga desnuda del electrón en electrodinámica cuántica (QED). En QED, la carga del electrón está protegida por pares virtuales electrón-positrón debido a las fluctuaciones cuánticas del vacío. En términos generales, se puede resumir: si el cristal se ablanda debido a la presencia de pares de dislocaciones virtuales, la probabilidad (fugacidad) de crear dislocaciones virtuales adicionales aumenta, proporcional al factor de Boltzmann de la energía central de una dislocación . Si hay dislocaciones adicionales (virtuales), el cristal se volverá aún más suave. Si el cristal es además más blando, la fugacidad aumentará aún más... y así sucesivamente. David Nelson, Bertrand Halperin y, de forma independiente, Peter Young formularon esto de manera matemáticamente precisa, utilizando la teoría de grupos de renormalización para la fugacidad y la elasticidad: En las proximidades de la transición de fase continua, el sistema se vuelve crítico, es decir, se vuelve autosimilar. en todas las escalas de longitud . Al ejecutar una transformación de todas las escalas de longitud por un factor de , la energía y la fugacidad dependerán de este factor, pero el sistema tiene que aparecer idéntico, simultáneamente debido a la autosemejanza. Especialmente la función energética (hamiltoniana) de las dislocaciones debe tener una estructura invariante. El ablandamiento del sistema después de una transformación de escala de longitud (alejar el zoom para visualizar un área más grande implica contar más dislocaciones) ahora está cubierto por una elasticidad renormalizada (reducida). La relación de recursividad para la elasticidad y la fugacidad es: ${\displaystyle y}$ ${\displaystyle y=e^{\frac {E_{C}}{k_{B}T}}}$ ${\displaystyle \gg a}$ ${\displaystyle l}$ ${\displaystyle E\to E(l)}$ ${\displaystyle y\to y(l)}$

${\displaystyle {\frac {dY^{-1}(l)}{dl}}={\frac {3}{2}}\pi y^{2}e^{Y(l)/8\pi }I_{0}{\Big (}Y(l)/8\pi {\Big )}-{\frac {3}{4}}\pi y^{2}e^{Y(l)/8\pi }I_{1}{\Big (}Y(l)/8\pi {\Big )},}$

${\displaystyle {\frac {dy(l)}{dl}}={\Big (}2-{\frac {Y(l)}{8\pi }}{\Big )}y(l)+2\pi y^{2}e^{Y(l)/16\pi }I_{0}{\Big (}Y(l)/8\pi {\Big )}.}$

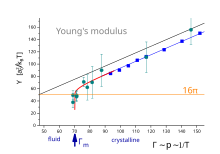
Se pueden derivar relaciones de recursividad similares para el módulo de corte y el módulo de volumen. y son funciones de Bessel , respectivamente. Dependiendo del punto de partida, la relación de recursividad puede tomar dos direcciones. No implica defectos, el conjunto es cristalino. , implica muchos defectos arbitrarios, el conjunto es fluido. La relación de recursividad tiene un punto fijo en con . Ahora es el valor renormalizado en lugar del simple. La Figura 2 muestra el módulo de Young en función del parámetro de control adimensional . Mide la relación entre la energía repelente entre dos partículas y la energía térmica (que fue constante en este experimento). Puede interpretarse como presión o temperatura inversa. La curva negra es un cálculo termodinámico de un cristal hexagonal perfecto en . La curva azul proviene de simulaciones por computadora y muestra una elasticidad reducida debido a las vibraciones de la red en . La curva roja es la renormalización que sigue a las relaciones de recursividad, el módulo de Young desaparece discontinuamente hasta cero en . Los símbolos turquesas provienen de mediciones de elasticidad en una monocapa coloidal y confirman el punto de fusión en . ${\displaystyle I_{0}}$ ${\displaystyle I_{1}}$ ${\displaystyle y\to 0}$ ${\displaystyle y\to \infty }$ ${\displaystyle y=0}$ ${\displaystyle E_{R}/k_{B}T=16\pi }$ ${\displaystyle E_{R}}$ ${\displaystyle \Gamma }$ ${\displaystyle T=0}$ ${\displaystyle T>0}$ ${\displaystyle 16\pi }$ ${\displaystyle Y_{R}=16\pi }$

Interacción entre declinaciones

Figura 3: Constante de Frank en la fase hexática: cae por debajo al fusionarse con el fluido isotrópico y diverge en la transición al cristal. ${\displaystyle 72/\pi }$

El sistema entra en la fase hexática después de la disociación de las dislocaciones. Para alcanzar el fluido isotrópico, las dislocaciones (5-7 pares) tienen que disociarse en disclinaciones , que consisten en partículas aisladas de 5 pliegues y de 7 pliegues. Se pueden utilizar argumentos similares para la interacción de las disclinaciones en comparación con las dislocaciones. Nuevamente, las disclinaciones sólo pueden crearse como pares debido a razones topológicas. Partiendo de la energía en función de la distancia entre dos disclinaciones se encuentra: ${\displaystyle H_{cli}}$

${\displaystyle H_{cli}=-{\frac {F_{A}\cdot \pi }{36}}\sum _{k\neq l}s({\vec {r}}_{k})\cdot s({\vec {r}}_{l})\ln {\frac {\Delta {\vec {r}}_{k,l}}{a}}+E_{s}\cdot N_{cli}.}$

El término logarítmico vuelve a predominar. El signo de la interacción produce atracción o repulsión para los números sinuosos y para las disclinaciones quintuplicadas y séptuples, de modo que las cargas de signo opuesto ejercen atracción. La resistencia general viene dada por la rigidez frente a la torsión. La constante de acoplamiento se denomina constante de Frank, siguiendo la teoría de los cristales líquidos . es la energía discreta de una dislocación para disociarse en dos disclinaciones. La distancia al cuadrado de dos disclinaciones se puede calcular de la misma manera, como para las dislocaciones, sólo se debe cambiar en consecuencia el prefactor, que denota la constante de acoplamiento. Divergencia para . El sistema se funde desde la fase hexática hasta el líquido isotrópico, si hay disclinaciones libres. Esta temperatura de transición viene dada por la constante de Frank: ${\displaystyle +\pi /3}$ ${\displaystyle -\pi /3}$ ${\displaystyle F_{A}}$ ${\displaystyle E_{s}}$ ${\displaystyle {\frac {F_{A}\cdot \pi }{36}}=4}$ ${\displaystyle T_{i}}$

${\displaystyle {\frac {F_{A}}{k_{B}T_{i}}}=72/\pi .}$

${\displaystyle 72/\pi }$es nuevamente una constante universal. La Figura 3 muestra mediciones de la rigidez orientacional de una monocapa coloidal; La constante de Frank cae por debajo de esta constante universal en . ${\displaystyle T_{i}}$

Exponentes críticos

Normalmente, las transiciones de Kosterlitz-Thouless tienen un continuo de puntos críticos que pueden caracterizarse por granos autosemejantes de regiones desordenadas y ordenadas. En las transiciones de fase de segundo orden, la longitud de correlación que mide el tamaño de esas regiones diverge algebraicamente:

${\displaystyle \xi =\xi _{0}{\Big (}{\frac {T-T_{c}}{T_{c}}}{\Big )}^{-\nu }}$.

Aquí, es la temperatura de transición y es un exponente crítico. Otra característica especial de las transiciones de Kosterlitz-Thouless es que la longitud de la correlación traslacional y orientacional en 2D diverge exponencialmente (ver también fase hexática para la definición de esas funciones de correlación): ${\displaystyle T_{c}}$ ${\displaystyle \nu }$

${\displaystyle \xi =\xi _{0}\cdot e^{{\Big (}{\frac {T-T_{c}}{T_{c}}}{\Big )}^{-\nu }}.}$

El exponente crítico se convierte en la longitud de correlación traslacional divergente en la transición hexático-cristalina. D. Nelson y B. Halperin predijeron que la constante de Frank también diverge exponencialmente con at . La curva roja muestra un ajuste de datos experimentales que cubren el comportamiento crítico; el exponente crítico se mide como . Este valor es compatible con la predicción de la teoría KTHNY dentro de las barras de error. Se predice que la longitud de la correlación de orientación en la transición hexático-isotrópica diverge con un exponente . Este valor racional es compatible con las teorías del campo medio e implica que no es necesaria una renormalización de la constante de Frank. No se debe tener en cuenta el aumento de blindaje de la rigidez de orientación debido a las disclinaciones; esto ya lo hacen las dislocaciones que se presentan frecuentemente en . Los experimentos midieron un exponente crítico de . La teoría KTHNY ha sido probada en experimentos ^{[10] [11] [12]} y en simulaciones por computadora. ^[13] Para la interacción de partículas de corto alcance (discos duros), las simulaciones encontraron una transición débil de primer orden para la transición hexático-isotrópica, ligeramente más allá de la teoría KTHNY. ^[14] ${\displaystyle {\bar {\nu }}=0{,}36963\dots }$ ${\displaystyle {\bar {\nu }}}$ ${\displaystyle T_{i}}$ ${\displaystyle {\bar {\nu }}=0{,}35\pm 0{,}02}$ ${\displaystyle \nu =0{,}5}$ ${\displaystyle T_{i}}$ ${\displaystyle \nu =0{,}5\pm 0{,}03}$

Referencias

1. Kosterlitz, JM; Sin embargo, DJ (1972). "Orden de largo alcance y metaestabilidad en superfluidos y sólidos bidimensionales". Revista de Física C. 5 : 124. doi : 10.1088/0022-3719/5/11/002.
2. Kosterlitz, JM; Sin embargo, DJ (1973). "Ordenamiento de metaestabilidad y transiciones de fase en sistemas bidimensionales". Revista de Física C. 6 (1181): 1181-1203. Código bibliográfico : 1973JPhC....6.1181K. doi :10.1088/0022-3719/6/7/010.
3. Halperin, BI; Nelson, DR (1978). "Teoría de la fusión bidimensional". Cartas de revisión física . 41 (2): 121-124. Código bibliográfico : 1978PhRvL..41..121H. doi : 10.1103/PhysRevLett.41.121 .
4. Nelson, DR; Halperin, BI (1979). "Fusión mediada por dislocaciones en dos dimensiones". Revisión física B. 19 (5): 2457–2484. Código bibliográfico : 1979PhRvB..19.2457N. doi : 10.1103/PhysRevB.19.2457.
5. Joven, Pensilvania (1979). "La fusión y el gas vectorial de Coulomb en dos dimensiones". Revisión física B. 19 (4): 1855–1866. Código bibliográfico : 1979PhRvB..19.1855Y. doi : 10.1103/PhysRevB.19.1855.
6. Kosterlitz, JM (1974). "Las propiedades críticas del modelo XY bidimensional". Revista de Física C. 7 (6): 1046–1060. Código bibliográfico : 1974JPhC....7.1046K. doi :10.1088/0022-3719/7/6/005.
7. Nelson, DR; Kosterlitz, JM (1977). "Salto universal en la densidad de superfluidos de superfluidos bidimensionales". Cartas de revisión física . 39 (19): 1201-1205. Código bibliográfico : 1977PhRvL..39.1201N. doi : 10.1103/PhysRevLett.39.1201 .
8. M. Kosterlitz: Nobelvortrag 2016
9. Kosterlitz, M. (2016). "Comentario sobre Ordenamiento, metaestabilidad y transiciones de fase en sistemas bidimensionales". Revista de Física C. 28 (48): 481001. doi : 10.1088/0953-8984/28/48/481001. PMID  27665689. S2CID  46754095.
10. Zanghellini, J.; Keim, P.; HH, von Grünberg (2005). "El ablandamiento de cristales coloidales bidimensionales". Revista de Física: Materia Condensada . 17 (45): 3579. Código bibliográfico : 2005JPCM...17S3579Z. doi :10.1088/0953-8984/17/45/051. S2CID  43231008.
11. Keim, P.; Maret, G.; von Grünberg, HH (2007). "La constante de Frank en la fase hexática". Revisión física E. 75 (3): 031402. arXiv : cond-mat/0610332 . Código bibliográfico : 2007PhRvE..75c1402K. doi : 10.1103/PhysRevE.75.031402. PMID  17500696. S2CID  5886990.
12. Gasser, U.; Eisenmann, C.; Maret, G.; Keim, P. (2010). "Fusión de cristales en dos dimensiones - mini reseña". ChemPhysChem . 11 (5): 963–970. doi :10.1002/cphc.200900755. PMID  20099292.
13. Jaster, A. (2004). "La fase hexática del sistema de discos duros bidimensionales". Letras de Física A. 330 (1–2): 120–125. arXiv : cond-mat/0305239 . Código bibliográfico : 2004PhLA..330..120J. doi :10.1016/j.physleta.2004.07.055. S2CID  119522893.
14. Kapfer, S.; Krauth, W. (2015). "Fusión bidimensional: de la coexistencia líquido-hexática a las transiciones continuas". Cartas de revisión física . 114 (3): 035702. arXiv : 1406.7224 . Código bibliográfico : 2015PhRvL.114c5702K. doi : 10.1103/PhysRevLett.114.035702. PMID  25659008. S2CID  9967752.